复杂环境背景下典型飞行器表面红外反射特性研究
2021-05-10孙建平王申领赵松庆郝燕云吴根水
孙建平,齐 宏,王申领,赵松庆,郝燕云,吴根水
(1.哈尔滨工业大学能源与科学工程学院,黑龙江 哈尔滨150001; 2.中国空空导弹研究院,河南 洛阳 471009;3.航空制导武器航空重点实验室,河南 洛阳 471009)
1 引 言
随着国防科技的发展,高速隐身战机在大国军事战略竞争中的地位变得举足轻重,而相对的制导则成为其中关键技术。目前的制导技术主要包括雷达制导、红外制导和地图定位制导等方法[1-4]。目前,随着计算机和红外传感器性能的提高及雷达反射面的逐渐减小,红外探测技术逐渐成为研究主流。
对于飞行器红外目标探测,国外研究较早且开发了相应计算软件。例如:美国RIT在美国DSC公司开发THERM模型基础上开发了DIRSIG红外仿真计算软件[5-6];美、英等国联合开发了可用于飞机红外信号仿真的NIRTRAN平台[7]。国内方面近年来发展迅速。例如:黄伟等[8-9]各辐射源及各种飞机飞行环境下的飞机蒙皮的红外反射特性进行了系统的分析研究,并认为蒙皮发射率对红外信号由很大影响;王霄等[10]和韩平丽等[11]分别对不同背景下的飞机进行了红外目标成像研究。
飞行器的红外目标探测以其表面的红外反射特性分布规律为基础,而飞行状态与飞行背景对飞行器表面反射特性具有重大影响,因此,本文采用有限元与商业软件结合的方法对不同飞行状态复杂背景下飞行器的表面红外反射特性的分布规律进行研究,以为飞行器的红外目标探测提供参考。
2 理论计算模型
2.1 Schlick模型
1982年,Schlick提出一种计算材料表面双向反射分布函数(BRDF)的数学模型,以表征不同材料的表面反射特性,具体可由式(1)表达[12]:
f(t,u,v,l,w)=Sλ(u)·D(t,v,l,w)
(1)
式中,Sλ表示入射方向函数,具体如式(2):
Sλ(u)=Cλ+(1-Cλ)(1-u)5
(2)
其中,Cλ表示波长反射因子。
式(1)中,D表示BRDF模型的方向因子,由式(3)表示:
(3)
式中,Z和A分别为关于变量r和变量p的极坐标函数;G(v)和G(l)分别为反射和入射的辐射遮挡因子,各函数具体表达式如式(4)所示:
(4)
式(1)~(3)中,变量t、u、v、l和w为Schlick模型中相应角度的余弦值,各变量具体表达式及相应角度的定义见文献[12],在此不再赘述。
2.2 坐标系转换及辐射遮挡判断因子计算
随着飞机的运动,飞机与探测器的相对位置一直在变化,同时对于飞机上单个面元来说,入射辐射方向与反射辐射方向也是不断变化的。因此,需要建立当地坐标系-飞机坐标系和飞机坐标系-面元坐标系之间的坐标转换关系,以此得到探测器接收到的辐射信号与飞机面元之间直接的对应关系。
飞机表面形状的复杂性与运动轨迹和姿态的多变性导致部分飞机表面入射辐射为0,且探测器接收到的辐射信号也会存在遮挡现象,因此本文引入了两个辐射遮挡判断因子来表征这一现象。
2.2.1 当地-地球坐标系
飞机所在地的太阳辐射初始入射方向取决于当地时间、当地纬度和季节等参数。飞机纬度信息则取决于飞机与地球的相对位置,因此,需要建立当地-地球坐标系描述这一关系。
建立以地球为参照的当地直角坐标系i-j-k,规定i轴方向为正面向西,k轴方向为地面法向,根据右手法则确定j轴方向,坐标原点为飞机所在位置P,如图1所示。
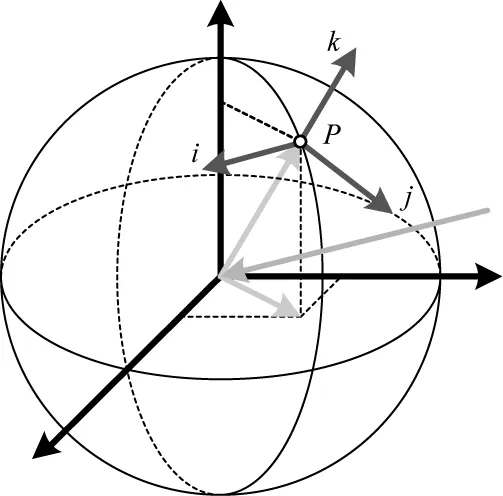
图1 当地-地球直角坐标系
2.2.2 飞机坐标系
飞机在飞行过程中存在旋转和仰角变化,且其飞行高度和飞行速度同样变化剧烈,其运动姿态和运动状态的多变性导致飞机表面获得的投射辐射方向不断变化。同时,由于飞机与探测器相对位置不断改变,探测器的探测方向也不断改变。因此,需要建立飞机坐标系,并明确当地坐标系-飞机坐标系之间的坐标转换关系。
建立飞机坐标系x-y-z,定义x轴方向为中轴线向后,y轴方向为水平面向右,右手定则确定z轴方向,如图2所示。

图2 飞机直角坐标系
则当地坐标系中坐标(i,j,k)与飞机坐标系中坐标(x,y,z)之间的转换关系如式(5)所示:
(5)
当飞机旋转时,其绕x、y和z轴的右旋角度分别为θx、θy和θz,于是式(5)中的转换矩阵可由式(6)表示:
(6c)
2.2.3 面元坐标系
BRDF的计算是在每一个飞机表面的面元上进行的,即需要得到每一个面元的入射辐射和反射辐射的方向参数,因此需要将飞机表面的入射辐射方向转化为每个面元的入射辐射方向参数,因而需要建立面元坐标系,并明确当地-飞机-面元之间坐标位置关系。
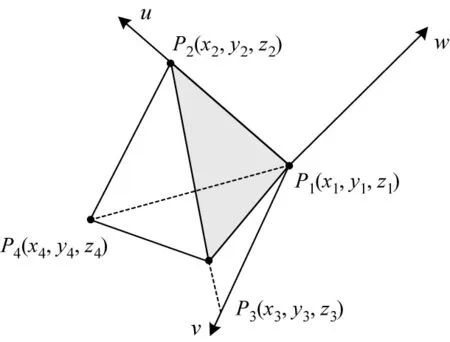
图3 面元直角坐标系
面元坐标系如图3所示。图中P1、P2、P3和P4组成了一个四面体网格,P1、P2和P3为飞机表面面元的三个顶点,P4为飞机内部节点,以此为基础,建立面元坐标系u-w-v,规则如下:
(1)u轴:P1为原点,向量P1P2方向为u轴方向,其方向余弦可由式(7)表示:
(7)
(2)w轴:面元外法向方向为w轴方向,可由面元面方程Ax+By+Cz+D=0与飞机内部点P4确定,如式(8):
(8)
式中,A、B和C为面元面方程系数,可根据P1、P2和P3坐标由式(9)确定:
(9)
(3)v轴:根据u轴与w轴,通过右手法则确定方向,其方向余弦如式(10):
(10)
三个坐标系确定后,结合式(5)可以确定飞机表面上某点在当地坐标系中的坐标(i,j,k)与其所在的面元坐标系的坐标(u,w,v)之间的转换关系,即式(11):
(11)
2.2.4 辐射遮挡判断因子计算
为判断单个面元是否有投射辐射和能否被探测器探测,本文引入投射辐射遮挡因子和探测遮挡因子,并利用反向蒙特卡洛法对这两遮挡因子进行计算。
在无其他飞机面元遮挡时,记投射辐射直接遮挡因子为Rs1和探测直接遮挡因子为Rd1,记由面元重心出发沿投射反方向(探测方向反方向)的追踪光束的方向向量为sis和面元法向量为ni,则Rs1和Rd1可由式(12)计算:
(12a)
(12b)
在考虑其他面元的遮挡时,记投射辐射间接遮挡因子为Rs2和探测间接遮挡因子Rd2。考虑面元j对面元i的遮挡情况,如图4所示。

图4 面元遮挡关系示意图
记面元i重心为G,沿投射辐射方向向量sis方向反向追踪光束交面元j于点R,则根据面元j面方程计算可得G到面元j距离lCR和面元j法向量与辐射方向夹角b,并由此得到GR距离lRG,进而求得R点坐标(xR,yR,zR)。最后根据R点与面元j其余三点组成的三角形面积是否与面元j本身面积相等判断R是否位于面元j内。若R位于面元j内,则Rs2和Rd2为0,否则为1。
记投射辐射遮挡因子和探测遮挡因子分别为Rs和Rd,综合直接与间接遮挡因子,则两遮挡判断因子可由式(13)计算:
(13)
2.2.5 红外探测模型
在近距离红外探测时,对于相同探测方向,飞机上不同面元相对于探测器的探测方向并不相同,因此需要建立探测模型,将以当地坐标系为基准的探测器探测方向转换为飞机坐标系为基础的探测方向。考虑100 m探测距离模型,如图5所示。
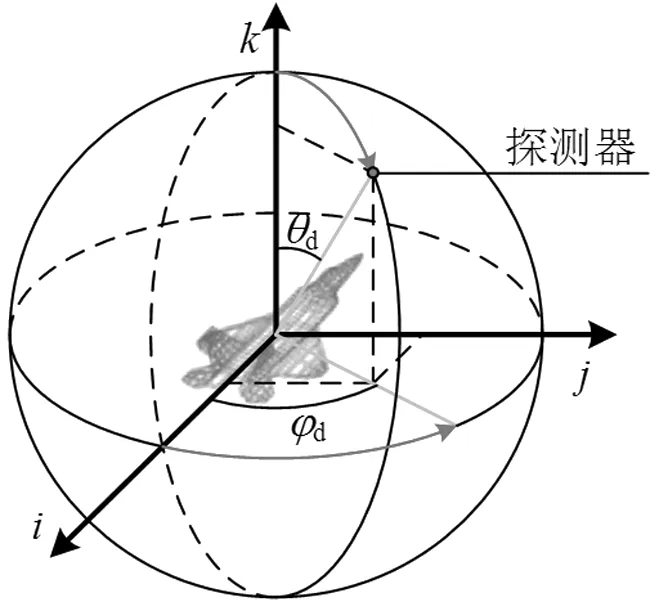
图5 红外探测模型
探测方向天顶角为θd,圆周角为φd,当地坐标系中探测点位置Pd(id,jd,kd)经过坐标转换可得飞机坐标系探测点位置Pdp(xd,yd,zd)和所在面元重心位置PGp(xGp,yGp,zGp),进而可以得到以飞机坐标系为基准的每个面元的探测方向,如式(14)所示:
(14)
式中,dp代表飞机坐标系中探测器位置;Gp代表飞机坐标系中面元重心位置。
最后,通过飞机坐标系与面元坐标系之间的转换,即有计算BRDF所需探测方向的天顶角θr和圆周角φr。
2.3 飞机表面投射辐射模型
2.3.1 太阳辐射
太阳赤纬δ0由飞行时的日期决定,可由式(15)计算:
式中,n为从1月1日起已经度过的天数。
太阳时角t0由飞行时刻决定,可由式(16)计算:
(16)
式中,t为一天中所处的时刻。
考虑飞行纬度对日出日落的影响,对飞机所处时刻位于日出前或日落后进行判断,如式(17):
(17)
式中,ω为飞机所在纬度。
当地坐标系中太阳入射辐射的天顶角θ和圆周角φ可由式(18)计算:
(18)
面元i获得的太阳投射辐射力可由式(19)计算:
(19)
式中,Rsun为太阳投射方向的遮挡因子;Esun为太阳辐射到地球表面的辐射照度(取635W/m2);Si为单个面元i的面积;θi为太阳辐射方向与面元i面法向向量夹角;Pir为太阳辐射直射比例(取0.75);BN,Tsun为N个谱带内太阳的黑体辐射力(本文太阳表面温度取5762 K)。
面元i反射的太阳直射辐射强度由式(20)计算:
(20)
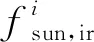
面元i获得的太阳散射辐射力由式(21)计算:
(21)
式中,Psc为太阳辐射中的散射比例,取0.25。
面元i反射的太阳散射辐射可由式(22)计算:
(22)
2.3.2 海面反射的太阳辐射
Cox与Munk[13-14]在1954年给出了海面反射率的计算模型,该模型较为复杂,在此只给出结论性公式(23),各变量含义及模型的具体内容见文献[13]和文献[14]。
(23)
式中,r为海面反射率,计算式(23)所需的大气折射率n1取1,海水折射率n2取1.334。
面元i获得的海面反射的太阳辐射由式(24)计算:
(24)
式中,re代表反射;τλ代表大气光谱透过率。
面元i对海面反射的太阳辐射的反射辐射强度由式(25)计算:
(25)
2.3.3 海面自身发射辐射
海面发生的辐射强度在本文的研究中并不占主导作用,因此可对海面自身发射的辐射模型进行一定简化[15]。认为海面自身发射为漫发射体,发射率为0.98,则面元i获得的海面自身发射辐射可由式(26)计算:
(26)
式中,sea代表海面自身发射的辐射。
面元i反射的海面自身发射辐射的辐射强度由式(27)计算:
(27)
2.3.4 大气辐射
大气本身存在一定自身发射辐射,可用式(28)计算:
(28)
式中,a、b为待定系数(分别取0.625、0.074[15]),γ为日期决定的季节角,可由式(29)计算:
γ=(n-1)·2π/365
(29)
式中,n与式(15)中含义相同。
则面元i反射的大气辐射可由式(30)计算:
式中,Tair代表大气温度。
综合式(15)~(30),可得面元i在探测方向的总反射辐射强度,如式(31)所示:
(31)
大气中的水和CO2对红外辐射具有较强的吸收作用,同时大气中的气溶胶颗粒等也会对传输中的辐射存在一定的散射作用,因此,对于远距离的大气辐射传输(例如:经由海面作用产生的辐射投射至高空的飞机表面过程)需要考虑计算大气透过率。
本文利用MODTRAN商业软件对2~5 μm波段和8~14 μm波段的大气透过率进行计算,计算条件为:飞行高度6 km,海拔高度0,探测天顶角150°,计算结果如图(6)所示。
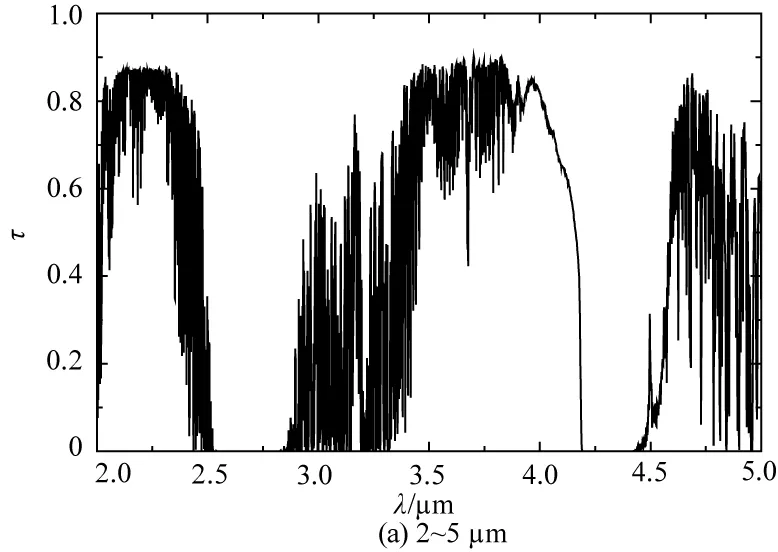
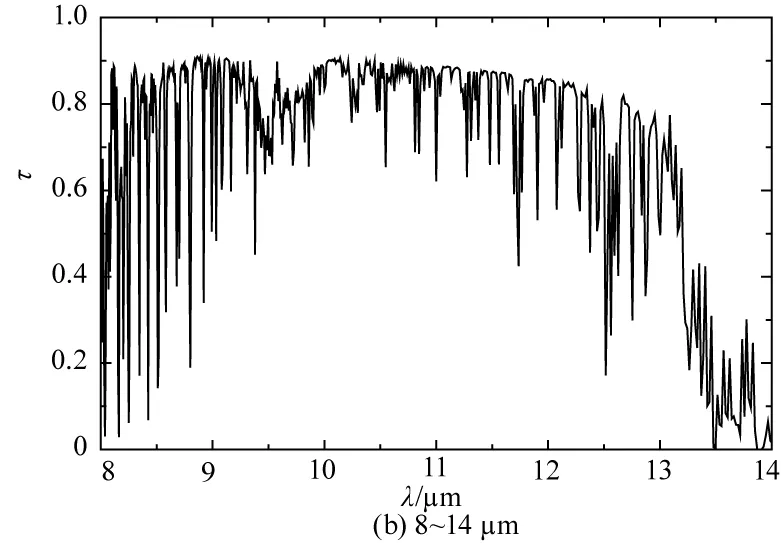
图6 不同波段大气透过率分布
3 飞机模型建立及计算网格划分
3.1 飞机几何模型
本文使用Catia商业软件中的Imagine&Shape模块和创成式设计模块,根据实际飞机尺寸绘制飞机几何模型,绘制结果如图7所示,比例为1∶1。

图7 绘制飞机模型与实际飞机模型
3.2 飞机计算网格
本文使用GID商业软件对飞机几何模型进行计算网格划分,在划分前,由于软件兼容性的问题需要对Catia软件中得到的飞机几何模型进行修补,而后进行网格划分,得到Triangle面元网格和Tetrahedra体元网格,划分结果用于反射辐射强度程序的调用计算。本文反射辐射强度计算结果的后处理也采用GID商业软件。
飞机几何模型及计算网格数据见表1,修补后的飞机几何模型及网格划分结果见图8。
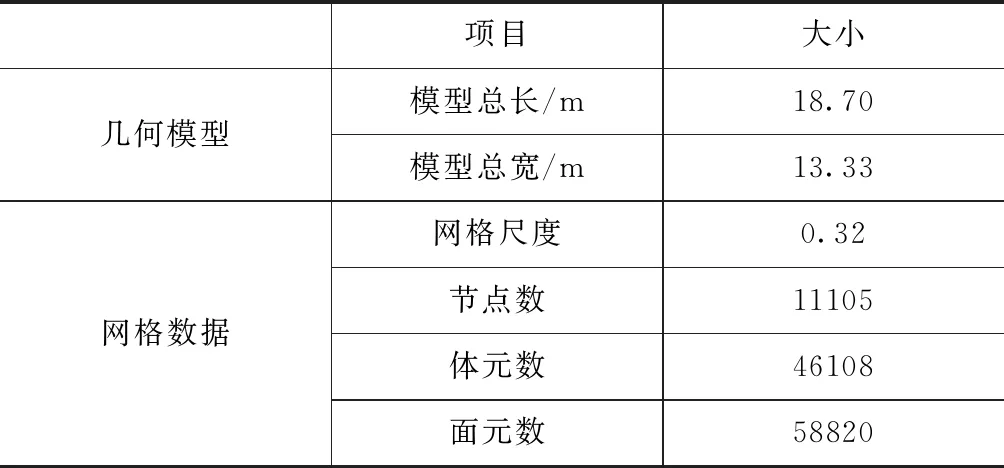
表1 飞机几何模型与计算网格数据表
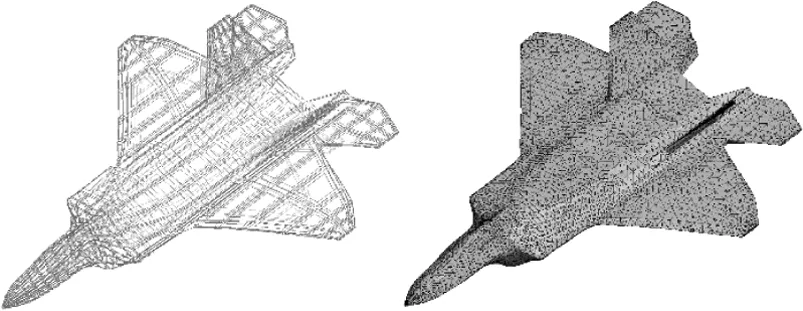
图8 修补后的几何模型及网格划分结果
4 结果与讨论
4.1 探测角度对飞机表面红外反射特性影响
本文首先对探测圆周角φr=270°不同探测天顶角条件下的飞机反射辐射分布特性进行了计算,计算条件如表2所示。
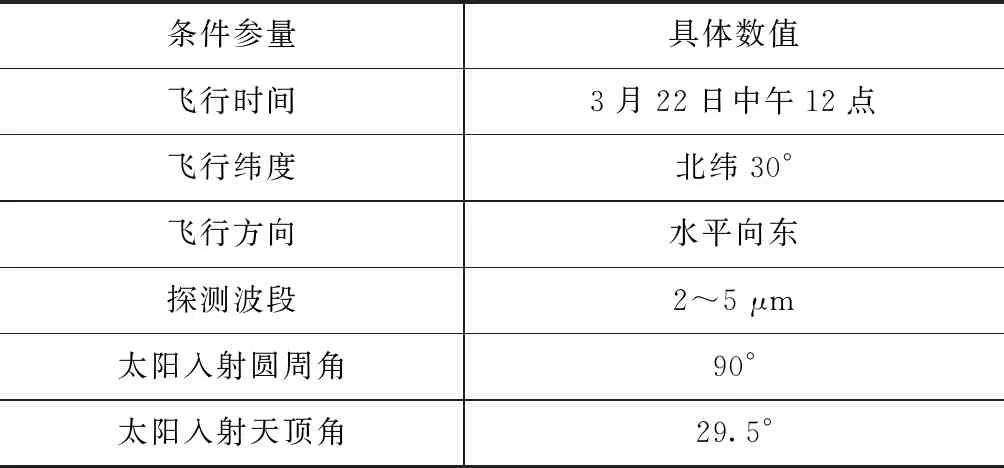
表2 不同探测角度下的计算条件参数
计算结果如图9所示,图9(d)中右侧箭头代表太阳辐射投射方向。综合分析图9(a)~(c)可以看到,随着探测天顶角度的变化,飞机的主要反射辐射源由飞机右翼、两翼和左翼逐次变化,出现这种现象是因为飞机表面几何结构复杂,采用BRDF模型计算时,飞机的主要辐射源出现在投射辐射与探测方向成镜面反射关系的位置处。
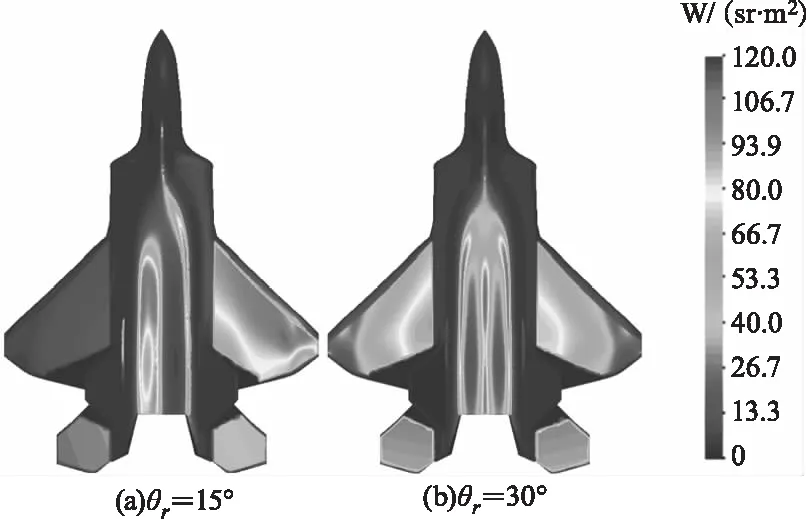
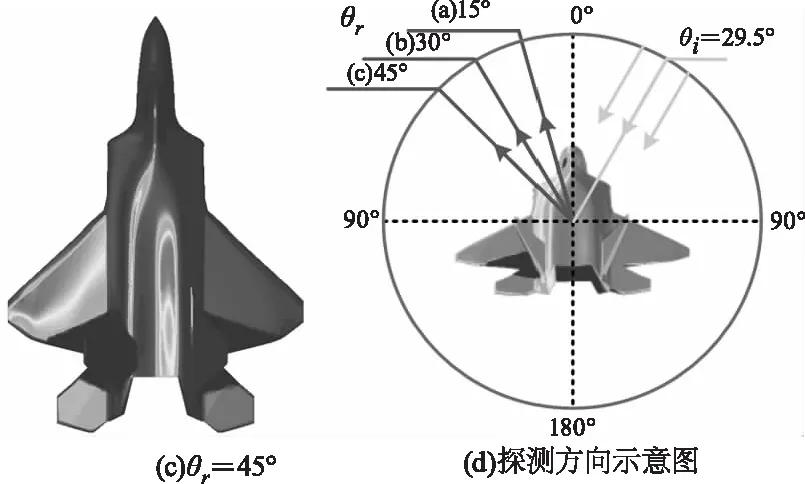
图9 不同探测天顶角反射辐射分布
图10为探测天顶角θr=30°不同探测圆周角情况下的飞机表面红外反射辐射分布计算结果。计算条件参数同表2,图10(d)中下方箭头代表太阳投射辐射方向。分析图10可知,随着探测圆周角的变化,飞机表面辐射源分布规律基本不变,集中在飞机两翼和中部机身位置(其余位置存在遮挡效应),但是其反射的强度由于远离镜面反射角度而逐渐降低。

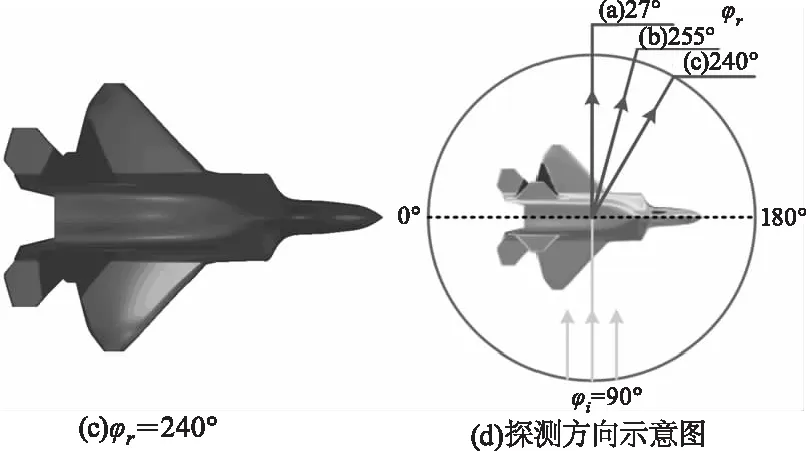
图10 不同探测圆周角反射辐射分布
4.2 飞机整体反射特性分析
针对特定探测平面对飞机红外反射特性进行了计算,计算条件参数与表2相同。图11为yoz平面不同波段不同探测天顶角下的飞机红外反射特性计算结果,其所得辐射强度为面元辐射强度与其面积作积并在特定方向上累加的结果。
从图11中可以看出,两波段上下表面反射强度分布相反,这是由于在2~5 μm波段太阳辐射强于海面辐射,而在8~14 μm波段海面辐射强于太阳辐射。在图11(a)中可以看到靠近与太阳入射方向成镜反射方向的方向附近辐射强度明显高于其他方向,凸显4.1小节描述的BRDF模型中的镜反射作用,图11(b)中的分布则是由于海面辐射正对向飞机下表面且飞机下表面的复杂性综合作用产生的。
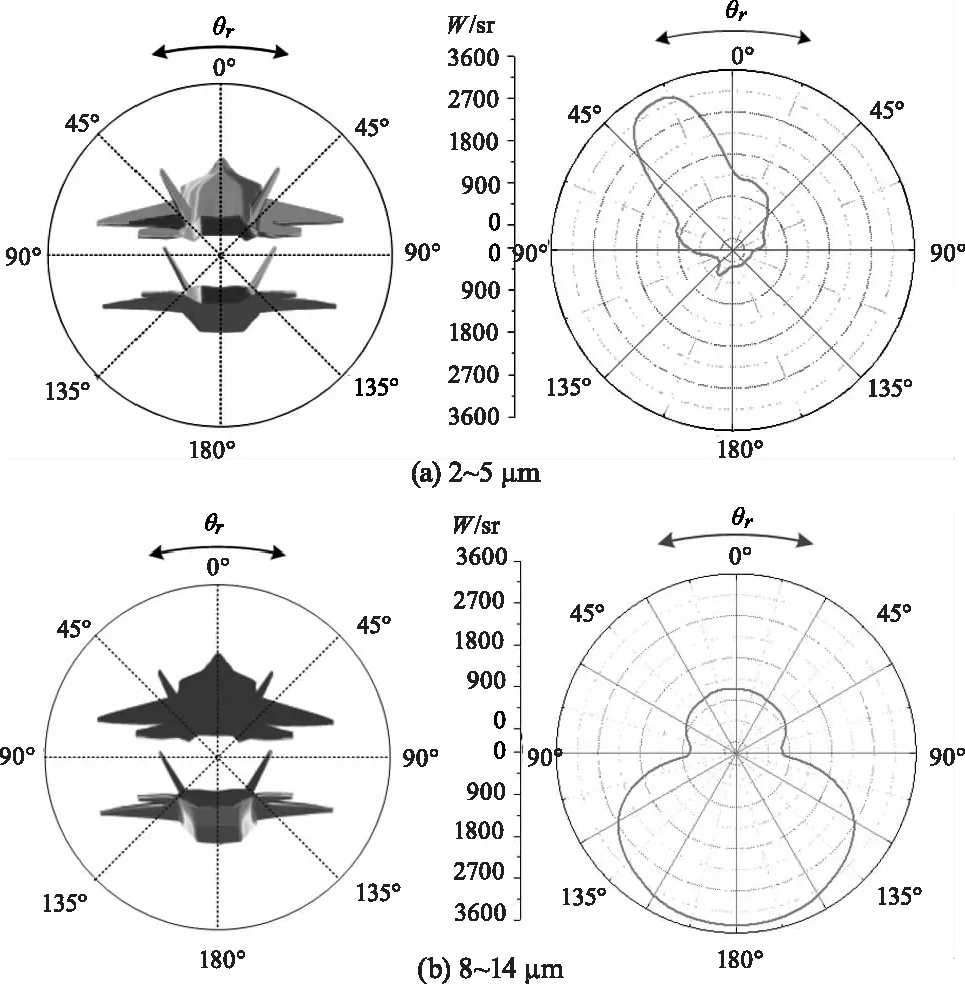
图11 yoz平面不同波段反射辐射强度分布
图12为2~5 μm探测波段下不同平面不同探测角度的飞机表面红外反射辐射特性分布计算结果,计算条件参数同表2。
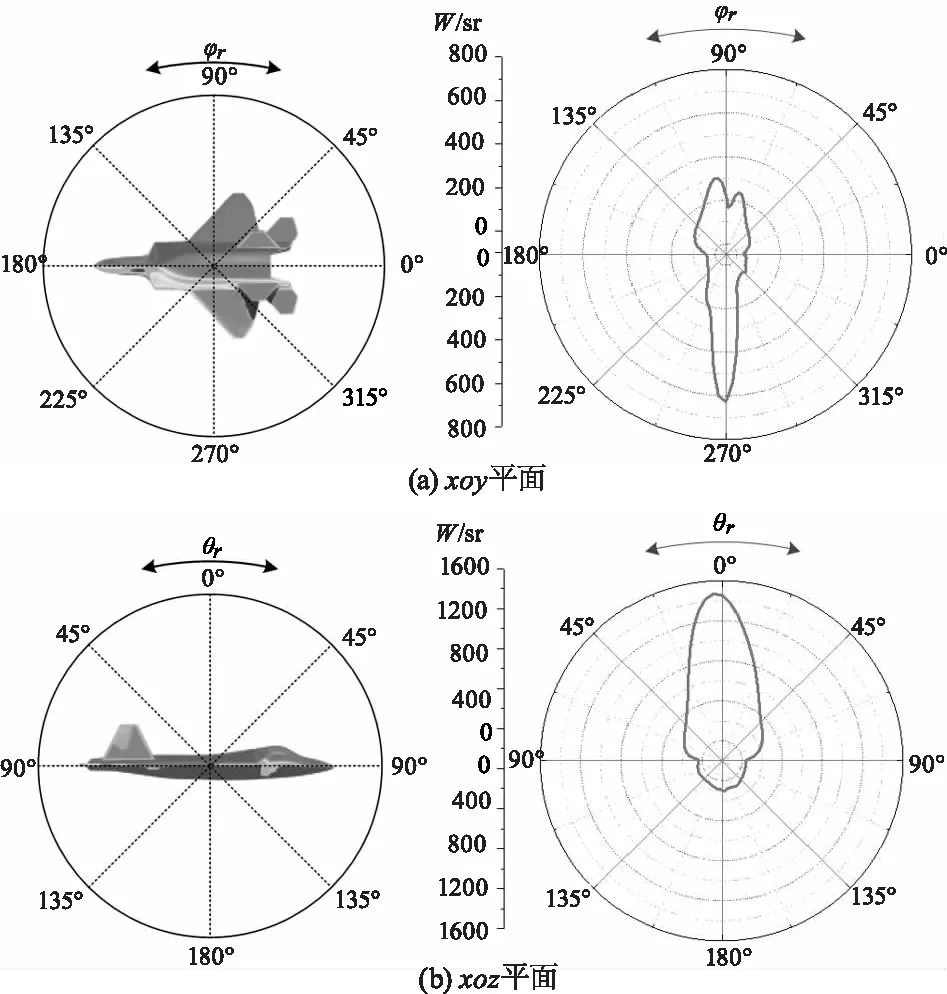
图12 2~5 μm波段不同平面反射辐射强度分布
从图12(a)中可以看出飞机的表面反射辐射主要集中与飞机主体及两翼,前端和后端反射很小,而从图12(b)中可以看到飞机前端与后端的反射基本相等,且由于太阳辐射的存在导致上端辐射比下端辐射更强,而这中分布建立在飞机水平飞行的基础上,所改变飞机姿态,则分布规律会发生相应改变。
5 结 论
本文采用有限元与商业软件结合的方法计算了海面背景下飞机表面红外反射特性分布情况,通过对计算结果的分析可以了解到,在BRDF模型下飞机表面镜面反射作用对飞机的表面红外反射特性分布影响较大,且太阳辐射与海面背景辐射在不同的探测波段分别起主导作用。
本文提出的计算方法并不局限于海面背景,对于不同的背景(如:沙漠、荒原或雪地等),只要获得相应背景的辐射模型,本文模型均有效,体现了本文所提出的计算方法的广泛适用性和有效性。
