基于有限元仿真的格构钢支柱振动状态分析

周 吉，马启明，刘继冬，吴积钦

0 引言

接触网是经由集电器向电力牵引单元提供电能的导体系统[1]，接触网支柱是接触悬挂的承载体，作为铁路供电系统最主要的竖向承力构件，其安全问题非常重要[2]。当外部因素造成接触网支柱发生振动时，其所承载的接触悬挂也会随之振动，受电弓经过时会对弓网运行状态造成一定影响，因此有必要对接触网支柱振动情况进行分析。

文献[2]对桥梁格构钢支柱进行了静力学分析、动力学分析，并引入到地震激励中获取其振动状态，研究了接触网支柱在地震作用下的性能状态，但具有一定特殊性且支柱系统性研究不完善。文献[3]中提到长台关大桥上接触网支柱与桥墩连为一体，桥梁振动引起接触网共振，支柱跟随桥体摆动，支柱振动波形传导到线索的振动幅度较大，最大时接触线跨中振幅可达200 mm，正馈线跨中振幅可达300 mm，造成线索磨损加剧，在承力索和正馈线钩头鞍子里发现大量断股现象，不利于弓网相互作用的稳定性。文献[4]对支柱及其挠度组成及影响进行定量分析，提出了支柱挠度设计标准建议，计算了风载荷下引起接触线高度的位置变化，但未考虑支柱振动对定位点处接触线高度的进一步影响。文献[5]对H型钢支柱提出了考虑土壤结构相互作用的三维结构的基本模态形状、固有频率及交叉现象。文献[6]介绍了不同车速下高速列车对H型钢支柱及接触线产生的地面传播振动的影响，但未对H型钢支柱振动进行详细阐述。基于上述情况，本文以电气化铁路桥梁区段中常见的13 m格构钢支柱为例，采用ANSYS有限元仿真软件对其振动状态进行详细分析，以探究支柱振动对接触网振动的影响。

1 格构钢支柱模型的建立

某既有线路桥梁区段采用全补偿简单链形悬挂，线索组合方式为THJ150+CTAH150，其中13 m格构钢支柱容量为G250/13，位于桥梁区段，采用正定位方式，定位点处水平分力为356.34 N，承力索定位点处水平分力为404.82 N，定位点处竖直载荷为81.438 N。考虑到实际运行过程中格构钢支柱通过搭载腕臂系统达到承载接触悬挂的目的，故将钢柱模型与腕臂系统看作一个整体进行分析。13 m格构钢支柱及腕臂系统材料属性如表1所示。

表1 格构钢支柱及腕臂系统材料属性

格构钢支柱实体模型及在ANSYS中建立的仿真模型如图1所示。

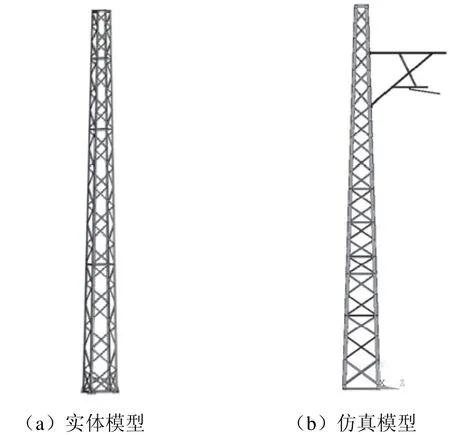
图1 格构钢支柱模型

在模型建立过程中，选取ANSYS全局坐标中的X方向为顺线路方向，选取全局坐标中的Y方向为格构钢支柱由低到高的方向即竖直方向，选取全局坐标中的Z方向为正定位拉出值所在方向。

2 格构钢支柱模型的验证

由GB/T 25020.1-2010《电气化铁路接触网钢支柱 第1部分：格构式支柱》可知，格构式钢支柱结构性能需满足标准检验弯矩下柱顶挠度不大于0.015倍的支柱高度要求；在承载力检验弯矩（标准检验弯矩的150%）下各部件不产生明显屈服[7]。本文中格构钢支柱的标准检验弯矩为250 kN·m，承载力检验弯矩为375 kN·m，柱高13 m。在校验标准检验弯矩时需在柱高12.9 m的位置沿着Z正方向施加19.38 kN的作用力；经仿真计算可知，在标准检验弯矩下柱顶挠度为35.971 mm，承载力检验弯矩下柱顶挠度为53.955 mm，二者均小于柱顶挠度极限值195 mm。由此可验证格构钢支柱模型的正确性。柱顶挠度如图2所示。

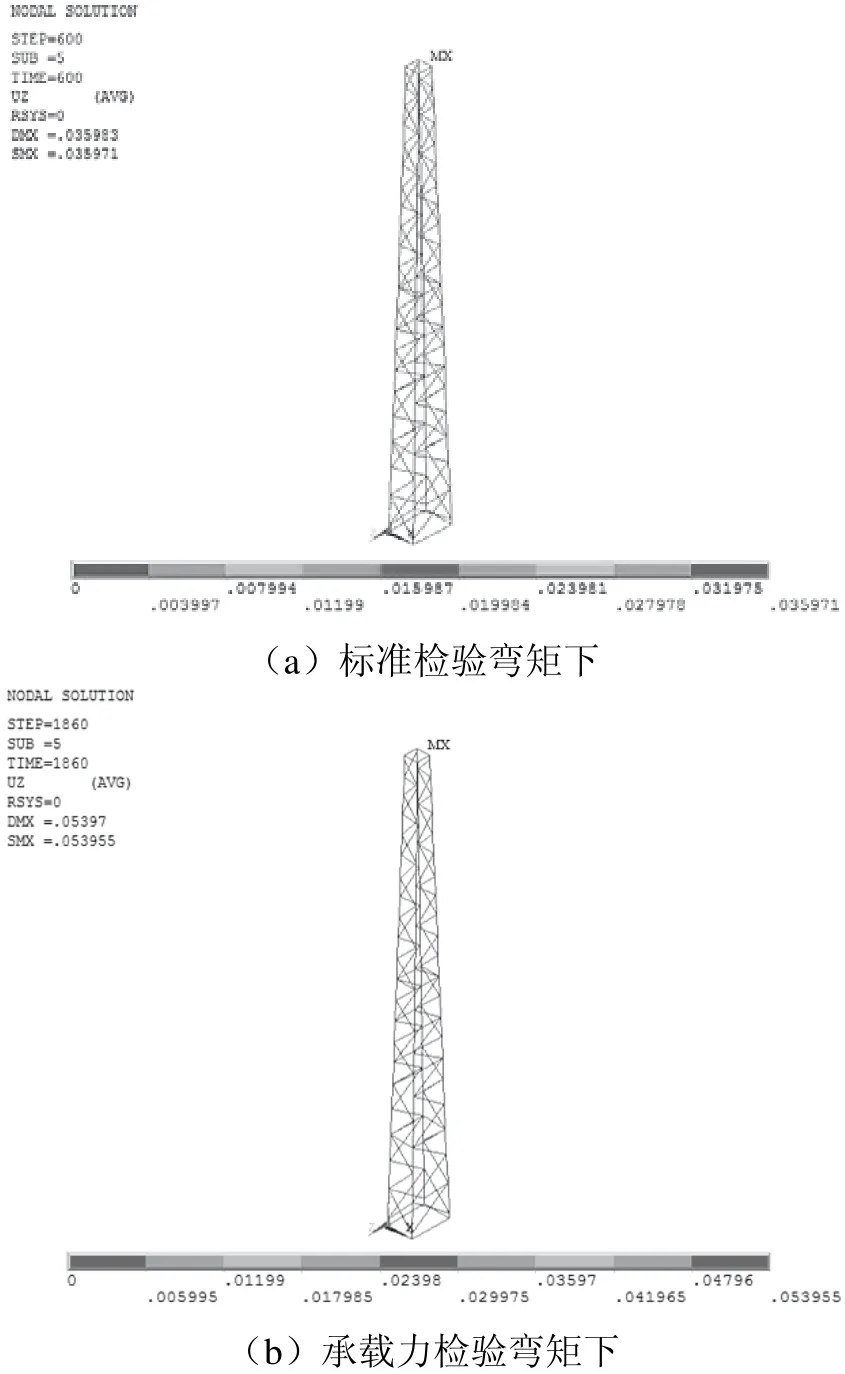
图2 格构钢支柱柱顶挠度

3 格构钢支柱静力学分析与模态分析

3.1 格构钢支柱静力学分析

选取的格构钢支柱质量为1 351.18 kg，在实际工况中，模型整体受到重力作用且定位点处、承力索定位点处受线索张力的水平分力作用，存在由定位线夹、部分接触线自重造成的竖直载荷。故在定位点处施加沿Z方向的水平分力356.34 N与沿Y负方向的竖直载荷81.438 N，在承力索定位点处施加沿Z方向的水平分力为404.82 N，对格构钢支柱进行静力学仿真，提取格构钢支柱整体的Y方向位移变化及应力分布，如图3、图4所示。

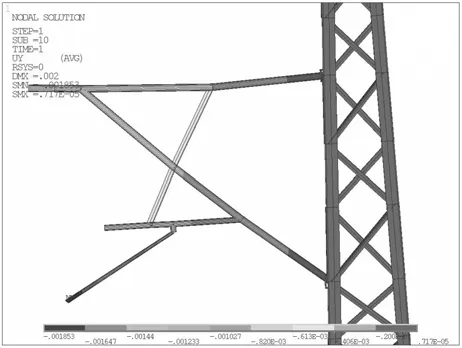
图3 格构钢支柱Y方向位移变化

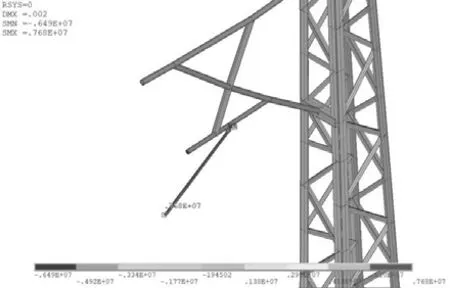
图4 格构钢支柱应力分布

由静力学仿真结果可知：Y方向最大位移出现在格构钢支柱的中部位置，其大小为0.003 91 mm；Y负方向最大位移出现在定位点处，其大小为1.848 mm。提取底部4个角肢柱的支反力及弯矩如表2所示。

表2 格构钢角肢柱支反力及弯矩

由表2可知：格构钢支柱前侧2个角肢柱受压力作用，左前角肢柱所受压力为7 226.82 N，右前角肢柱所受压力为7 221.10 N；后侧2个角肢柱受拉力作用，左后角肢柱所受拉力为573.10 N，右后角肢柱所受拉力为573.24 N；角肢柱的最大弯矩为28.22 N·m；应力最大位置出现在定位器连接的定位点处，应力为7.68 MPa；平腕臂所受最大水平拉力为814.178 N，最大应力为1.38 MPa。由静力学仿真可知，格构钢支柱模型整体处于低应力弹性状态。

3.2 格构钢支柱模态分析

格构钢支柱系统的固有频率取决于结构的刚度以及质量。模态分析可以预估结构在某频段内由外部或内部各种振源作用产生的实际振动响应，是谐波响应分析的基础。在静力学分析的基础上，为了解格构钢支柱的自振频率及振型，需要对其进行数值模态分析[8]。本文采用Block Lanczos法对格构钢支柱进行八阶模态分析并提取对应的频率（表3）及振型（图5）。

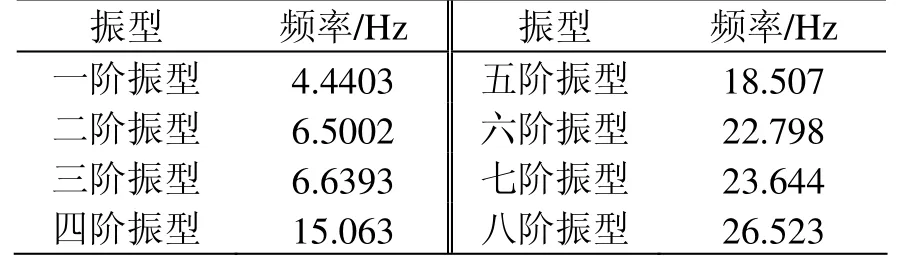
表3 格构钢支柱八阶模态振型频率

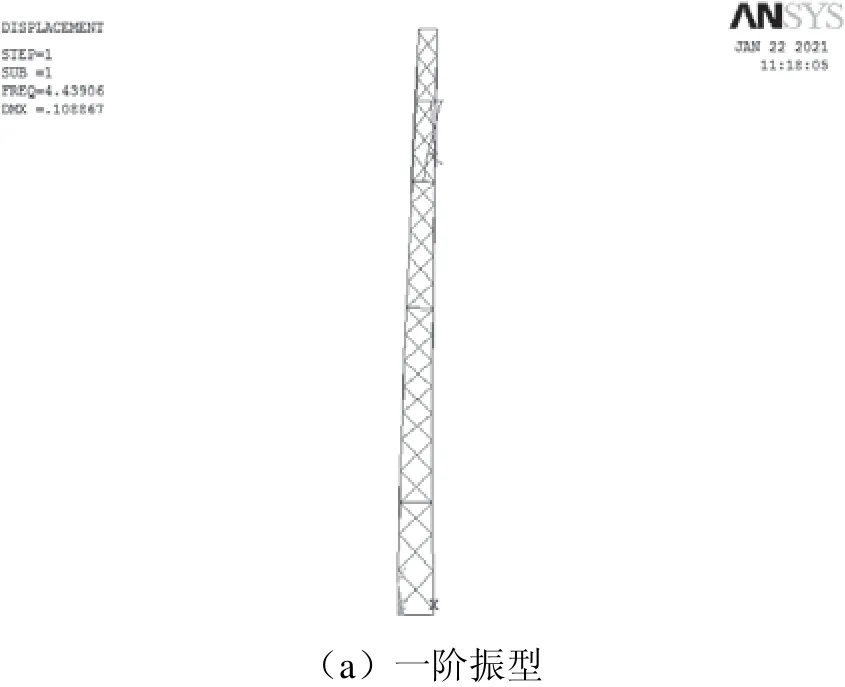
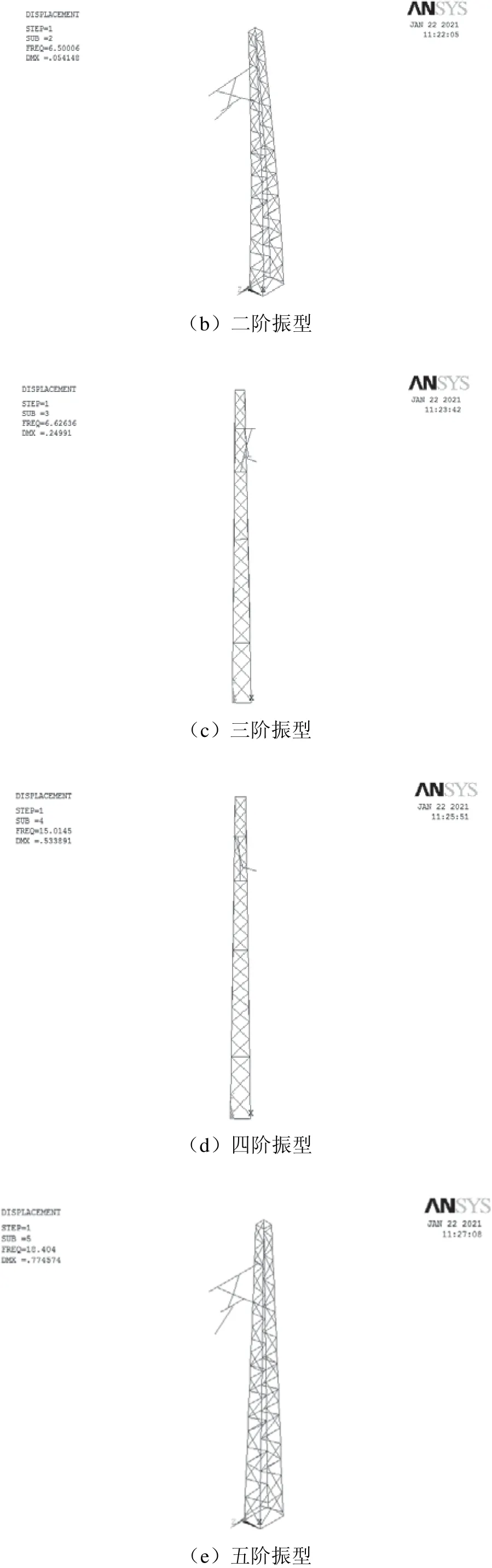
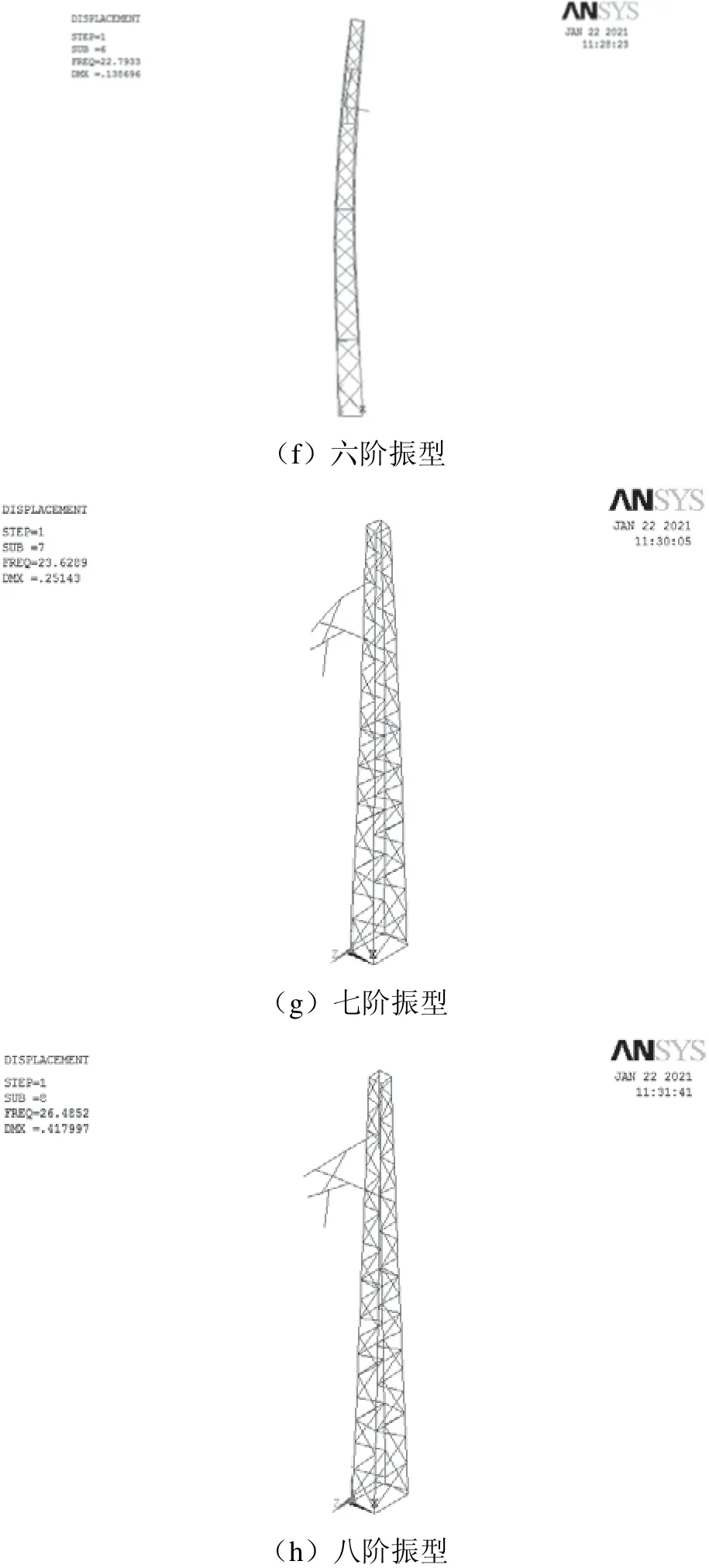
图5 格构钢支柱振型

第一阶振型时格构钢支柱上半部与腕臂系统在XY平面内顺线路方向摆动，对应频率为4.439 06 Hz；第二阶振型时格构钢支柱整体（包括腕臂系统）会在YZ平面内沿拉出值方向发生弯曲变形，对应频率为6.500 06 Hz；第三阶振型时格构钢支柱会在XY平面内逆线路方向摆动且腕臂系统会顺线路方向摆动，对应频率为6.626 36 Hz；第四阶振型时平腕臂会在XY平面内逆线路方向摆动而定位器顺线路方向摆动，对应频率为15.014 5Hz；第五阶振型时腕臂系统局部振动明显，定位器会在YZ平面内沿竖直方向摆动，对应频率为18.404 Hz；第六阶振型时格构钢支柱会在XY平面内顺线路方向弯曲变形且定位管逆线路方向摆动，定位器顺线路方向摆动，对应频率为22.793 3 Hz；第七阶振型时格构钢支柱会绕Y轴顺时针发生扭曲变形且平腕臂与定位器在XY平面内顺线路方向摆动，定位管、斜撑、斜腕臂逆线路方向摆动，对应频率为23.628 9 Hz；第八阶振型时格构钢支柱会绕Y轴逆时针发生扭曲变形且平腕臂与定位器在XY平面内顺线路方向摆动，定位管、斜撑、斜腕臂逆线路方向摆动，对应频率为26.485 2 Hz。为进一步探究格构钢支柱在外界作用力频率为4.439 06～26.485 2 Hz时对应的振动情况，需要对格构钢支柱进行谐波响应分析。

4 格构钢支柱谐波响应分析

由格构钢支柱基底微动造成的格构钢支柱振动，可看作格构钢支柱产生加速度时具有的惯性力。惯性力会使物体有保持原有运动状态的倾向，而此时若以该物体为参考系，并在该参考系上建立坐标系，此时就仿佛有一股方向相反的力作用在该物体上，使该物体在坐标系内发生位移[9]。本文以外加作用力模拟格构钢支柱基底微动产生的惯性力，采用完全法求解谐波响应，分析结构响应与载荷之间的传递特性，获取格构钢支柱在几种频率下的响应，并得到响应随频率变化的曲线，以预测格构钢支柱的持续动力特性。

4.1 理论分析

频域下线性系统动力学方程[10，11]为

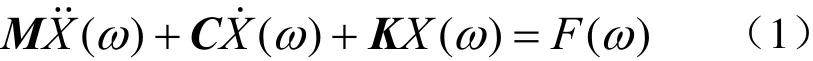
式中：M、C、K分别为格构钢支柱系统的质量矩阵、阻尼矩阵、刚度矩阵；分别为系统的绝对加速度响应、绝对速度响应和绝对位移响应；F(ω)为系统的外部作用载荷。

由于格构钢支柱系统中既存在约束节点又存在非约束节点，因此，可按照约束节点与非约束节点分块[12，13]，可将式（1）写为

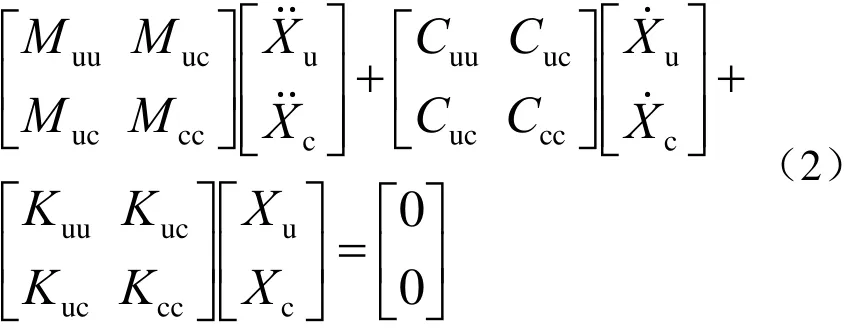
式中：用角标“u”表示非约束节点集合，用角标“c”表示约束节点集合；分别表示非约束节点集合的绝对加速度响应、绝对速度响应和绝对位移响应；分别表示约束节点集合的绝对加速度响应、绝对速度响应和绝对位移响应；Muc、Cuc、Kuc分别为单元耦合质量、耦合阻尼和耦合刚度。

从而可知非约束节点集合的动力学方程为

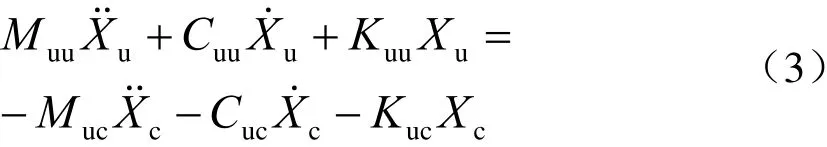
使用完全法即可按照式（3）对格构钢支柱的顶点、平腕臂安装点以及定位点的位移进行求解。

4.2 实例计算

为模拟格构钢支柱基底微动造成的格构钢支柱产生加速度时所具有的惯性力，在格构钢支柱基底角肢柱位置施加沿Z正方向的作用力，频率为2～30 Hz，大小分别为500 N（平均每个角肢柱施加125 N），1 000 N（平均每个角肢柱施加250 N）与1 500 N（平均每个角肢柱施加375 N），计算步数为50步，即步长频率为0.56 Hz，阻尼比为0.02。继而获取格构钢支柱顶点、平腕臂安装点在X、Y、Z3个方向的位移变化，如图6、图7所示。

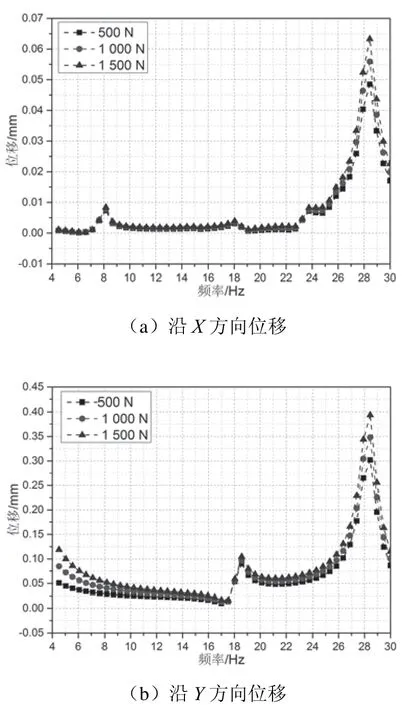
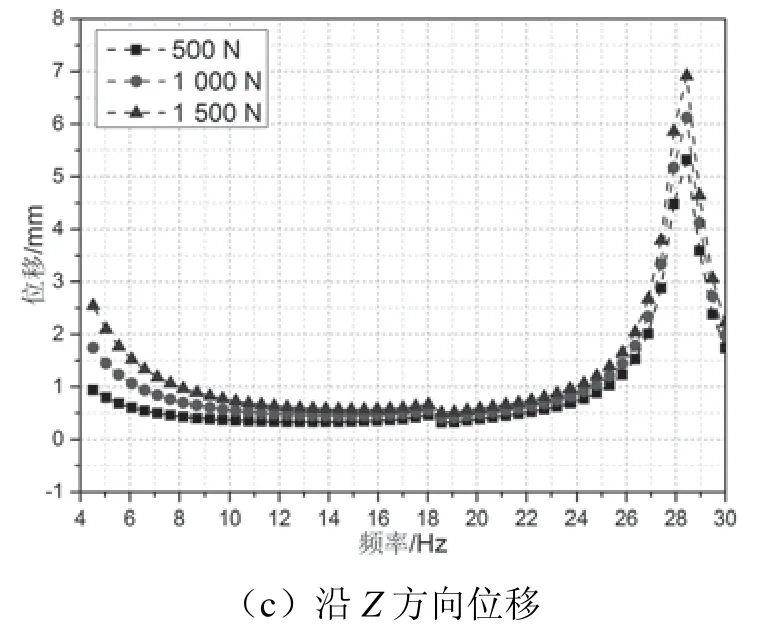
图6 支柱顶点位移变化

从格构钢支柱顶点位置来看，该位置随作用力的增加并不会产生较大的位移变化，在基底部位施加1 500 N作用力下该位置沿X方向的最大位移仅为0.063 mm，沿Y方向的最大位移仅为0.4 mm，沿Z方向的最大位移为7 mm，作用力的频率均为28.44 Hz，对应为格构钢支柱的第八阶固有频率。可知在基底部位施加28.44 Hz频率的作用力时，格构钢支柱顶点位置在X、Y、Z3个方向的位移最大，并且位移随着作用力大小的增加而逐渐增加，但由于格构钢支柱整体以焊接为主，整体刚度较大，且处于低应力弹性状态，故支柱顶点在X、Y方向位移基本可以忽略。虽然作用力沿Z正方向，支柱顶点在Z方向的最大位移为7 mm，远小于柱顶挠度极限值195 mm。

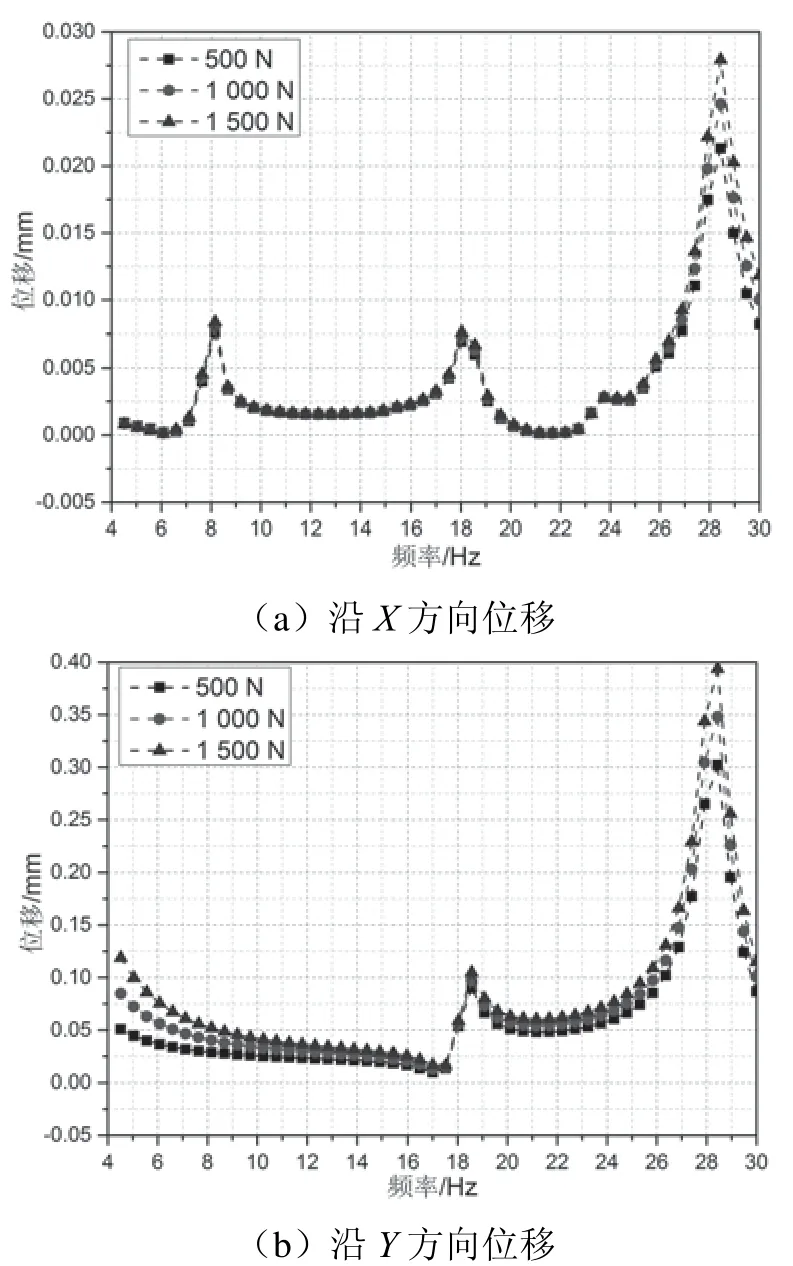
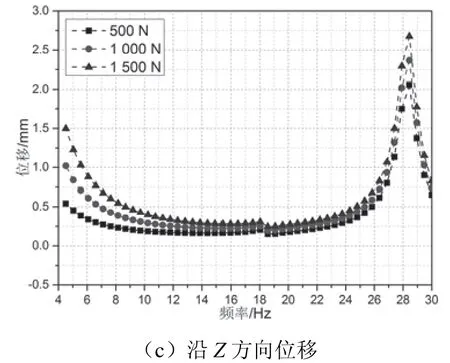
图7 平腕臂安装点位移变化

从平腕臂安装点位置来看，该位置随作用力的增加同样不会产生较大的位移变化，在基底部位施加1 500 N作用力下该位置沿X方向的最大位移仅为0.026 7 mm，沿Y方向的最大位移仅为0.393 7 mm，沿Z方向的最大位移为2.68 mm，作用力的频率均为28.44 Hz，对应为格构钢支柱的第八阶固有频率。但由于格构钢支柱整体刚度较大，处于低应力弹性状态，平腕臂安装点高度小于支柱顶点高度，斜腕臂以及斜撑会对平腕臂起到支撑的作用，缓解平腕臂安装点受到的由平腕臂自重引起的弯矩影响。正因如此，虽然作用力沿Z正方向，平腕臂安装点在Z方向的最大位移（2.68 mm）要小于支柱顶点在Z方向的最大位移（7 mm）。

格构钢支柱顶点以及平腕臂安装点在X、Y、Z3个方向的位移均在基底作用力频率为28.44 Hz时最大，但是位移量均较小，格构钢支柱较为稳定。进一步观察支柱振动对定位点处的影响，绘制定位点处在X、Y、Z3个方向的位移变化如图8所示。

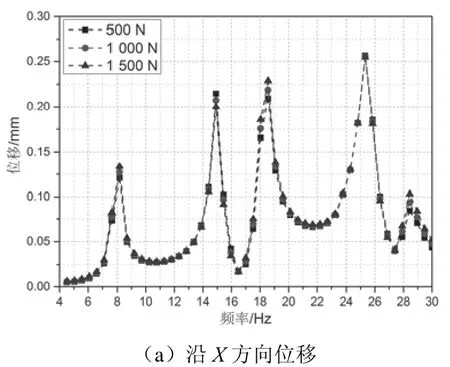
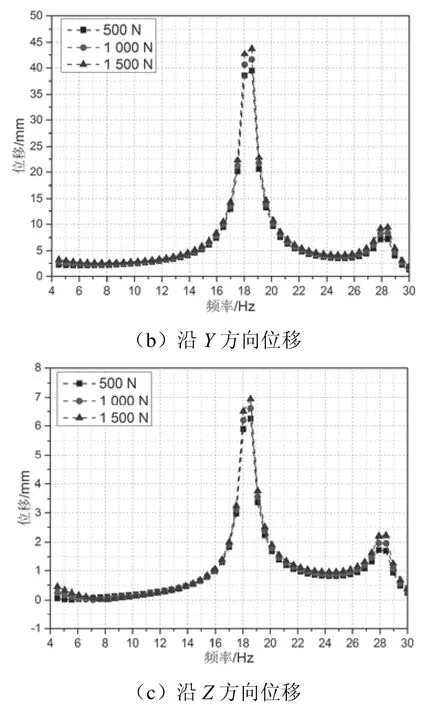
图8 定位点处位移变化

定位点处X方向位移基本不会随支柱基底Z正方向作用力的增大而增大，但是会随着作用力的频率达到系统整体四阶固有频率、五阶固有频率、七阶固有频率、八阶固有频率而形成多个峰值，但最大位移仅为0.255 mm，即定位点处沿X方向位移基本可以忽略；定位点处Y方向位移会随基底作用力的增大而增大，当作用力为1 500 N且频率为18.56 Hz时，对应第五阶固有频率，定位点的振动位移达到43.77 mm，振动较为显著，易造成弓网离线，对弓网相互作用稳定性造成影响；定位点处Z方向位移虽然会随作用力的增大而增大，但增量不明显，在基底Z正方向1 500 N作用力下最大位移为6.94 mm，小于拉出值误差上限30 mm[14]，不会对定位点处的拉出值造成太大影响。

进一步绘制定位点处应力与应变如图9所示。由图9可知：随作用力频率的增大，定位点处应力会在第五阶和第八阶固有频率附近出现峰值，并且随着作用力的增大，峰值逐渐增加；当作用力为1 500 N，频率为18.56 Hz时，定位点处最大应力为134.9 MPa，相比于静力状态下应力增大了127.22 MPa。由于钢结构焊件、铸钢及有色金属零件的安全系数不小于3.0[15]，则材质编号为Q235A型的定位器在定位点连接处的许用应力为78.33 MPa，因此当基底作用力频率为17～20 Hz时，定位点处的应力会超过其许用应力（但未超过屈服强度），产生应力集中，对其寿命造成影响。定位点处存在沿Z正方向的水平分力，会造成定位器末端产生轴向应变，当基底作用力为1 500 N、频率为27.6 Hz时，产生最大轴向应变响应为3.14×10-6mm/mm。定位器所连接的接触线在自重的作用下会对定位器末端产生弯曲应变，该应变会随着基底作用力频率的变化在第四阶、五阶、七阶、八阶固有频率处产生多个峰值，最大弯曲应变为10.1×10-6mm/mm。

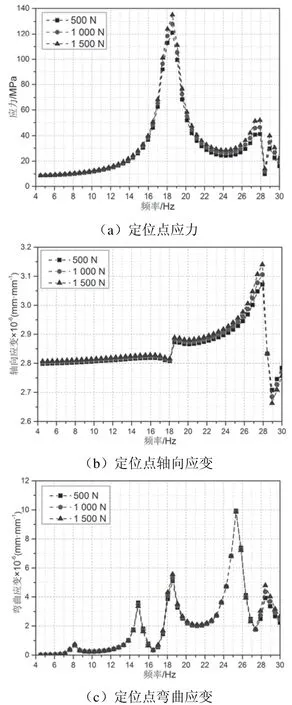
图9 定位点处应力与应变

5 结论

本文对接触网设施中常见的13 m格构钢支柱进行建模分析，得到以下结论：

（1）通过静力学分析可知，13 m格构钢支柱-腕臂系统最大Y方向位移出现在格构钢支柱的中部位置，为0.003 91 mm，应力最大位置为定位器连接的定位点处，支柱基本无变形，处于低应力弹性状态。

（2）对格构钢支柱-腕臂系统进行数值模态分析可知，其一阶固有频率为4.4403 Hz，二阶固有频率为6.500 2 Hz，三阶固有频率为6.639 3 Hz，四阶固有频率为15.063 Hz，五阶固有频率为18.507 Hz，六阶固有频率为22.798 Hz，七阶固有频率为23.644 Hz，八阶固有频率为26.523 Hz。

（3）在格构钢支柱基底角肢柱位置施加沿Z正方向的作用力，频率为2～30 Hz，大小分别为500 N（平均每个角肢柱施加125 N），1 000 N（平均每个角肢柱施加250 N）与1 500 N（平均每个角肢柱施加375 N）。经过谐波响应分析可知，由于格构钢支柱整体以焊接为主，整体刚度较大，斜腕臂以及斜撑会对平腕臂起到支撑作用，即使基底受到频率为28.44 Hz沿Z正方向1 500 N的作用力，支柱顶点与平腕臂安装点在X、Y2个方向的位移基本可以忽略，沿Z方向位移也均未超过7 mm，格构钢支柱整体较稳定。定位点处Y方向位移会随基底作用力增大而增大，当作用力为1 500 N且频率为18.56 Hz时，对应第五阶固有频率，定位点Y方向振动位移达43.77 mm，振动较为显著，易造成弓网离线，证明支柱振动会加剧接触网振动，不利于弓网作用稳定性。定位器末端应力为134.9 MPa，超过其许用应力（未超过屈服强度），对寿命造成一定影响。后续有必要对支柱振动状态下弓网动态作用进行深入研究。