置孔释压支护材料孔型排列方式研究

张 博，李彦斌,2，韦庆量，谷 攀

(1.太原理工大学 矿业工程学院，山西 太原 030024；2.中国矿业大学(北京) 深部岩土力学与地下工程国家重点实验室，北京 100083)

随着煤矿开采深度逐年增加，深部越来越多的巷道在高地应力、松散软弱的岩层中掘进[1-4]，传统刚性支护变形协调性差，支护强度低，难以适应深部高应力软岩巷道变形特点，极易出现锚杆(锚索)滑脱折断、锚网破网、U型钢支架扭曲变形等现象，迫使企业投入大量人力物力对巷道进行多次翻新维护[5-9]。为有效控制围岩变形，降低深部高应力软岩巷道返修率，李彦斌教授提出了置孔释压一次成巷支护技术[10-12]，孙雁新、吴智勇等又分别从孔形选择与材料布置形式等方面对置孔释压材料做了改进研究[13-14]。但目前置孔释压支护技术仍有不足之处，需要完善提升。

从巷道能量转化角度阐述了置孔释压支护原理，并基于孔距、孔径等置孔参数对置孔释压材料塑性区边界的影响，对不同孔型排列方式下的置孔释压材料进行力学实验，确定了置孔释压材料最佳孔型排列方式，进一步优化了置孔释压支护技术。

1 深部高应力软岩巷道能量转换

在高地应力、松散软弱的岩层中，岩体积聚了大量原始势能，巷道开挖扰动打破了能量初始平衡状态[15]，随着围岩内部能量释放，岩体在强度低、应力集中、能量聚积的地方发生形状和体积的改变，产生弹性或塑性变形甚至破裂崩解。M.D.G.Salamon将岩体视作均质连续介质，列出了地下岩体能量守恒表达式：

Wc+Um=Wr+Uc

(1)

式中：Wc为地下原岩应力因开挖扰动而做的功；Um为挖出岩体释放的应变能；Wr为开挖过程中损耗的弹性能；Uc为岩体重新积聚的应变能。

在对式(1)进一步分析后，陶振宇[16]认为在许多情况下，只要岩体性质和硐体形式确定，Wc、Um与Wr可被近似认为不变。同时，巷道等硐体在开挖过程中除损耗一部分弹性能外，还会损耗另一部分非弹性能Wn，构筑支护措施后，支护结构也要吸收一部分能量Wf。能量守恒公式改写如下：

(2)

(3)

(4)

Wf+Wx=const

(5)

式中Wx为诱发巷道围岩变形破坏的能量。

根据式(5)，增大Wf会降低能量Wx的积聚程度，从而保持围岩稳定。但传统刚性支护需要在增加支护成本前提下，通过提高支护强度才能使Wf增大[17]。因此，针对深部高应力软岩巷道，合理的支护方式应当能够有效提高支护结构能量吸收能力，而又不必付出巨额支护成本。置孔释压支护正是通过设置柔性置孔释压材料来达到这一目的的。

2 新型置孔释压支护技术

2.1 置孔释压支护方法

置孔释压支护体系构建方法如图1所示。

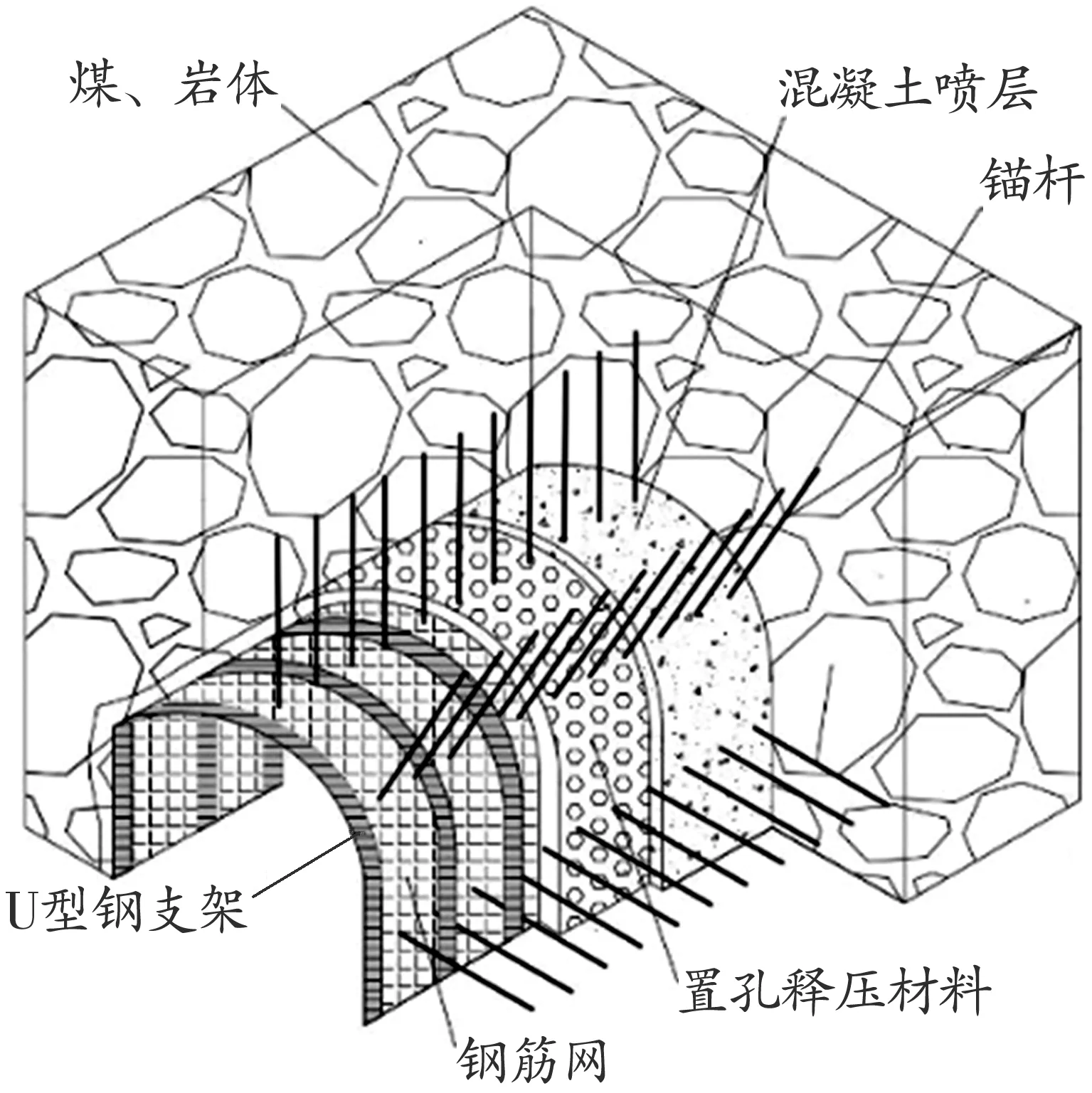
图1 置孔释压支护体系剖视图

1)巷道开挖后，立即进行锚喷支护，对围岩进行封堵。

2)根据围岩应力状况，留足释压空间层，在释压层中放置对应大小置孔释压材料。其中，置孔释压材料是一种新型可压缩支护材料，由粉煤灰、 煤矸石与不饱和聚酯树脂混合而成，在材料成型过程中通过预置一定样式的圆孔和添加剂，使材料具有抗压强度高﹑让压空间大﹑能量吸收性强等特点。

3)在释压层表面架设由U型钢支架与钢筋网相互连接构成的金属支架层，起到强力支撑作用。

该方法通过上述构架，将置孔释压材料紧密填充在围岩与金属支架之间，利用其特殊力学性能和结构特征实现与围岩的变形协调，体现了围岩—释压材料—支护体的协同作用原理。

2.2 置孔释压支护原理

在深部高应力软岩巷道中，当切向应力高于围岩应力时会在巷道周围形成一部分应力增高区，围岩受挤压影响而逐渐被压密甚至压碎，能量Wx正是在围岩挤压变形和破坏过程中得到积聚。置孔释压支护原理如图2所示。

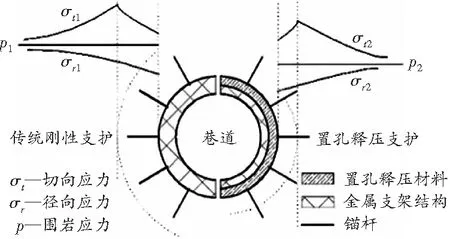
图2 置孔释压支护原理

相较于传统刚性支护，置孔释压支护通过合理架构使置孔释压材料与巷道围岩紧密接触，利用释压材料在高应力条件下主动受压变形代替部分围岩变形，从而减小能量Wx的积聚程度。同时随着围岩变形对释压材料做功，支护结构吸收的能量Wf得到增加，Wx进一步降低，置孔释压材料经被开始压缩至完全压密，可以释放掉大部分围岩应力，大幅改善切向应力、径向应力及整体围岩应力环境，使巷道围岩高应力状态转变为低应力状态，确保围岩与其他支护体的承载力得以有效发挥，进而实现巷道的长期稳定。

3 置孔释压材料孔型排列方式选择

3.1 置孔释压材料力学分析

在置孔释压支护系统中，置孔释压材料承担了系统吸收的大部分围岩能量，当高应力作用在置孔释压材料上时，材料发生塑性变形，吸收的能量又分为两部分[18]：

Wf=Wmf+Wsf+Wzf

(6)

Wsf=Wc+Wn

(7)

式中：Wmf、Wsf、Wzf分别为锚杆、置孔释压材料和金属支架层吸收的围岩能量；Wc、Wn分别为置孔释压材料塑性变形过程中储存和消耗的围岩能量。

根据式(7)，若置孔释压材料自身塑性区越大，则其变形吸收消耗的围岩能量就会越小。因此，置孔释压材料自身塑性区大小成为影响其支护效果的直接原因。为便于分析材料塑性边界特点，建立置孔释压材料力学模型，如图3所示。设其所受压力为p，测压系数为λ，所置圆孔半径均为r，相邻圆孔间距分别为d1、d2、d3。

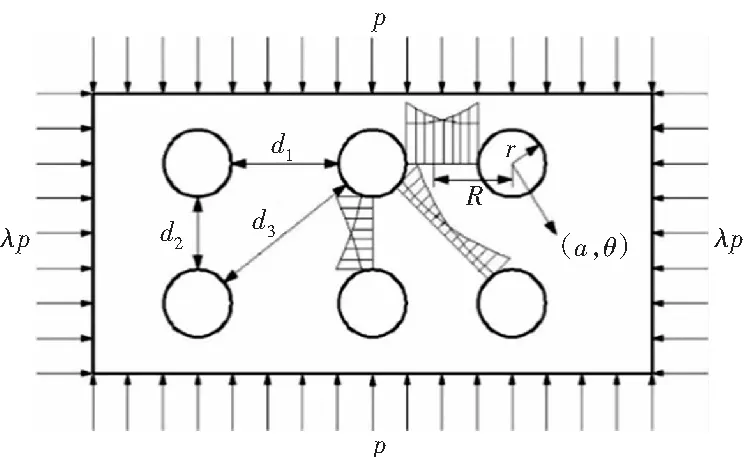
图3 置孔释压材料力学模型图

根据弹塑性力学理论，若相邻圆孔孔距d1、d2、d3均超过2倍影响半径R，则预置圆孔之间不会产生应力叠加效应。置孔影响半径计算公式如下：

(8)

则极坐标下置孔释压材料预置圆孔附近任意一点(a、θ)处的切向应力σt、径向应力σr、剪应力τtr为：

(9)

将式(9)代入Mohr-Coulomb屈服准则中，经过推导可得出无应力叠加状态下置孔释压材料自身塑性区边界隐性方程[19]：

(10)

式中C、φ分别为置孔释压材料的黏聚力和内摩擦角。

根据式(10)，当置孔释压材料所受压力及自身属性(黏聚力和内摩擦角)一定时，改变其孔型排列方式，材料塑性区边界会跟随所置圆孔的孔距、孔径等变化而发生改变，但塑性区边界计算过程过于繁琐，从力学角度无法直接推算究竟何种孔型排列方式的置孔释压材料塑性区分布范围最小，支护效果最佳。

3.2 不同孔型排列方式实验对比

结合实际应用，根据释压材料圆孔预置参数公式(11)的要求，按图4制作6种不同孔型排列方式的置孔释压材料，分组测定抗压强度及可连续变形量。

l1l2l3ω=nπr2li

(11)

式中：l1、l2与l3分别为置孔释压材料的3个边长，为降低尺寸效应干扰，本次实验材料边长均取100 mm；ω为置孔率，取0.35；n为孔数；li为置孔深度，取l1、l2或l3。

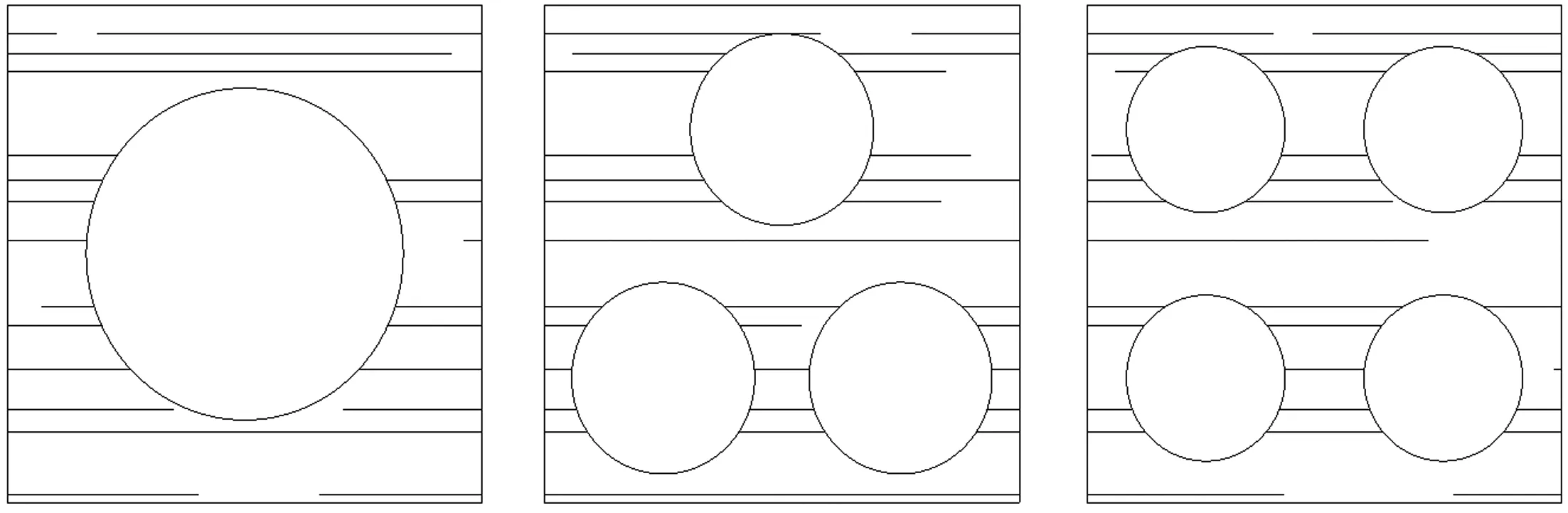
(a)单孔排列(b)三角形排列 (c)正方形排列

(d)菱形排列(e)梅花形排列 (f)长方形排列

每种孔型排列方式的试件3块为一组，依次用JL-WAW60伺服万能试验机进行压缩实验。其中正方形排列方式的置孔释压材料实验过程如图5所示。从图5(a)中可以看出，实验初期，圆孔饱满未发生明显改变，材料仅依靠自身强度就可抵抗压力作用；当压力加载至27 MPa时，圆孔出现变形，材料开始释压，此状态标志着材料已达自身强度极限，见图5(b)；随着加载范围不断扩大，材料承受压力越来越高，圆孔出现了明显变形,见图5(c)；当压力加载至 36 MPa 时，圆孔闭合程度接近一半，材料逐渐被压实，释压能力变弱,见图5(d)。

(a)22 MPa (b)27 MPa

(c)31 MPa (d)36 MPa

同理，对其他孔型排列方式的置孔释压材料进行压缩实验观察，6组材料的应力—应变曲线如图6所示。

图6 不同排列方式的置孔释压材料应力—应变曲线

由图6可知：无论采用何种孔型排列方式，置孔释压材料应力—应变曲线皆呈现出3个阶段的“阶梯状”特征。第一阶段：弹性阶段，压力作用前期，置孔释压材料近似呈线弹性变形；第二阶段：释压阶段，置孔释压材料自身强度小于围岩应力，材料压缩变形释放压力；第三阶段：释压材料被彻底压实、破坏后，剩余压力可通过支架承担。研究表明：当材料强度超过30 MPa时会使金属支架等支护体产生较大变形，达不到支护目的；当强度低于20 MPa时材料则不易产生连续释压，易出现冲击破坏现象[20]。因此，当可连续压缩量无明显区别时，在合理区间内按照抗压强度就高不就低的原则进行判断，正方形排列方式的置孔释压材料更满足支护要求。

4 置孔释压支护工程实践应用

山西介休青云煤矿埋深680 m，020202轨道平巷属于深部高应力软岩巷道，设计掘进断面宽4 000 mm，高3 850 mm，原支护方案如图7(a)所示。

(a)原支护方案

(b)置孔释压支护方案

顶板：锚杆采用ø20 mm×2 000 mm左旋螺纹钢锚杆，锚索采用ø18.8 mm×8 500 mm钢绞线；两帮：锚杆采用ø20 mm×1 800 mm圆钢锚杆，锚索采用ø17.8 mm×4 300 mm钢绞线；金属支架所用U型钢为29 U。目前巷道出现明显变形，锚杆、锚索及 U型钢支架等支护结构开始不同程度被损坏。

现采用正方形排列方式的置孔释压支护方案对巷道围岩重新进行控制，其中：顶部和两帮全部选择ø20 mm×2 000 mm左旋螺纹钢锚杆，金属支架选择U29型钢制作，围岩与金属支架间紧密充填单块规格为200 mm×200 mm×400 mm的置孔释压材料，具体布置如图7(b)所示。

两种支护方案的巷道围岩塑性区FLAC3D数值模拟结果如图8所示，从图8中可以看出，原支护方案下巷道塑性区在两帮与底板处厚度尤深，围岩承载力严重下降；采用正方形排列方式的置孔释压支护方案后塑性区范围缩小至围岩浅部位置，有利于巷道的长期稳定。

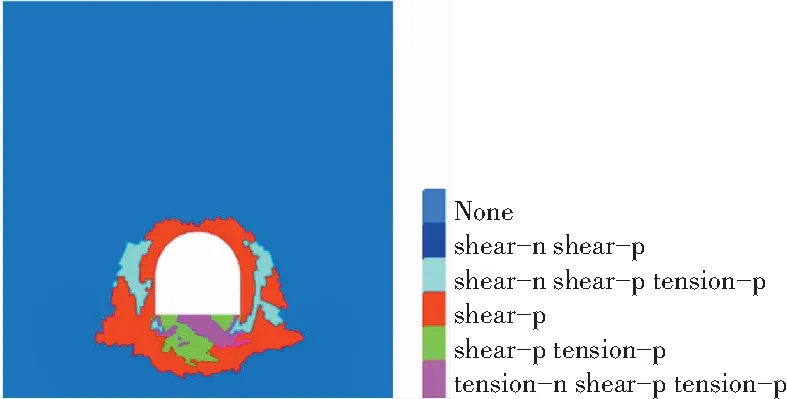
(a)原支护方案

(b)置孔释压支护方案

在020202轨道平巷中，对置孔释压支护方案下的巷道顶底板及两帮位移量进行监测，并与原支护方案进行比较，两种支护方案的位移收敛计的监测结果如图9所示。

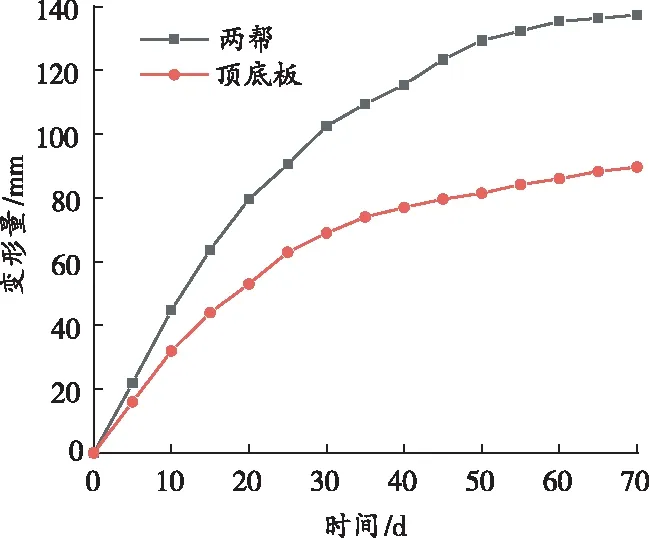
(a)原支护方案

(b)置孔释压支护方案

由图9可知：原支护方案下，巷道支护35 d后尽管围岩变形速率减小，但变形仍在持续增加，最终的巷道顶底板变形量达89 mm，两帮变形量达到 138 mm，变形严重需要及时返修；而采用正方形排列方式的置孔释压支护方案35 d后，围岩变形得到有效控制，巷道顶底板变形量为23 mm，两帮变形量也仅为 41 mm，两处变形量降幅均达到70%以上。因此，置孔释压支护能有效控制深部高应力围岩变形。

5 结论

1)针对深部高应力软岩巷道围岩控制问题，相较于传统刚性支护，置孔释压支护依靠置孔释压材料压缩变形吸收和消耗围岩能量，改善围岩应力状态，有效发挥出围岩和支护体承载力，体现了围岩—释压材料—支护体的协同作用原理，达到巷道长期稳定目的。

2)根据材料塑性区边界隐性方程的推导过程，孔距、孔径等置孔参数都会对置孔释压材料的支护性能造成影响，并基于对6种不同孔型排列方式的置孔释压材料抗压实验，分析得出正方形排列方式的释压材料抗压强度最符合高应力软岩巷道支护要求，正方形排列方式是置孔释压材料的最佳孔型排列方式。

3)通过实际应用得出，采用正方形排列方式的置孔释压支护方案比原刚性支护方案巷道顶底板及两帮收敛变形量减小70%，进一步验证了置孔释压支护的合理性。