长壁工作面沿空留巷充填墙体宽度模拟研究

2021-05-10高玉龙

矿业安全与环保 2021年2期

高玉龙

(晋能控股煤业集团马道头煤业有限公司，山西大同 037003)

根据相关统计研究发现，我国70%以上的国有煤矿为高瓦斯矿井，存在瓦斯治理难题[1-2]。近年来伴随着煤炭资源高产高效开采，瓦斯排放量也呈现出逐年增大的趋势。瓦斯在采掘空间内积聚易造成局部瓦斯浓度升高，进而易引发井下人员瓦斯中毒、矿井火灾甚至瓦斯爆炸等严重事故[3-5]。我国进行的煤矿瓦斯灾害防治，以煤层瓦斯预抽措施为主。虽然对煤层采取地面或者井下瓦斯预抽措施后能够在一定程度上减少煤层瓦斯涌出量，但受煤层透气性能及井下复杂开采系统布置的影响，容易在工作面上隅角等位置形成瓦斯积聚现象[6-7]。

仅采用传统的瓦斯预抽措施，已经很难适应现有煤矿安全高效的开采节奏。长壁工作面Y形通风采用“两进一回”的通风方式[8-9]，在提高煤炭资源采出率的同时，还能有效优化进回风路线，避免工作面上隅角出现瓦斯积聚现象，因此在有条件的矿井采用工作面Y形通风布局方式能够更好地解决工作面瓦斯积聚的难题。

1 工程地质概况

山西大同唐山沟煤矿主采8#煤层，煤层平均埋深超过430 m，煤层平均厚度和倾角分别为3.5 m和5°。8#煤层瓦斯含量为8.63～15.49 m3/t，大于我国规定的8 m3/t的瓦斯突出煤层临界含量，表明煤层开采期间会存在较大的瓦斯灾害问题。为解决工作面上隅角瓦斯积聚问题并提高煤炭资源回采率，在N8205工作面(N为北翼采区，8为煤层编号，205为工作面编号)实施了沿空留巷措施。N8205工作面走向长为1 351 m，倾向长为211 m。随着N8205工作面的推进，轨道平巷通过沿空侧时充填墙体被保留下来，形成沿空巷道。N8205工作面轨道平巷和胶带平巷均可用于进风，而沿空巷道用于回风。N8205工作面两进一回“Y”型通风系统布置方式如图1所示。

图1 工作面两进一回“Y”型通风系统

2 沿空巷道围岩物理力学特性

2.1 充填墙体材料物理力学特性

为了检验由膏体充填材料制成的充填墙体的完整力学性能，对标准试件进行单轴压缩试验。不同养护时间试件的单轴抗压强度如图2所示。

图2 不同养护时间试件的单轴抗压强度

由图2可知，养护时间为7 d时试件的单轴抗压强度已占最终强度的74.8%，强度增长速度较快，已满足现场需求。最终现场充填墙体的最佳养护时间确定为7 d。

2.2 岩体物理力学特性

岩体取芯后的力学性能测试参数不能直接应用于数值模型中，这是因为岩芯通常没有明显节理和缺陷，并不能客观描述岩体的力学特征。数值模型通常尺寸较大，因此需要代入岩体的力学参数进行模拟运算。笔者基于广义Hoek-Brown破坏准则，开发了RocLab 10.0软件[10]，利用岩芯的测试参数来确定对应岩体的力学特性。存在节理的岩体的广义Hoek-Brown准则为[11-12]：

(1)

式中：σ1、σ3分别为最大、最小有效主应力，MPa；σc为岩芯的单轴抗压强度，MPa；mb、s和a均为岩体常数。

岩体常数mb、s和a的计算公式如下：

(2)

(3)

(4)

式中：mi为岩芯的材料常数；D为取决于爆炸损伤和应力松弛引起的扰动程度的因子；I为估算存在节理的岩体力学性能常数。

变形模量E与常数I的关系如下：

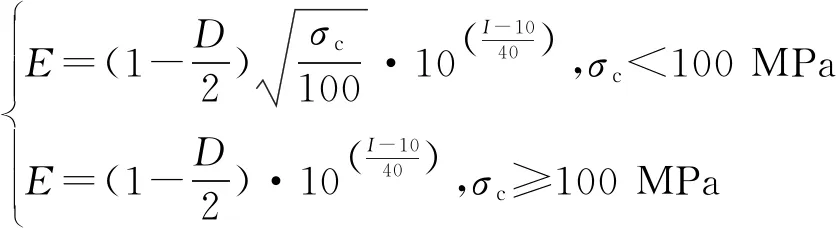
(5)

根据式(5)得到的变形模量，体积模量K和切变模量G可根据泊松比μ计算得到：

(6)

而抗拉强度σt可由下式计算得到：

(7)

本研究中，I和mi直接从表中查得；σc由单轴压缩试验获得；巷道在服务期内会受到工作面回采引起的严重动载扰动影响，因子D取值为0.7；选择应用方案为“隧道”，埋深为430.9 m。

岩体的物理力学特性参数如表1所示。

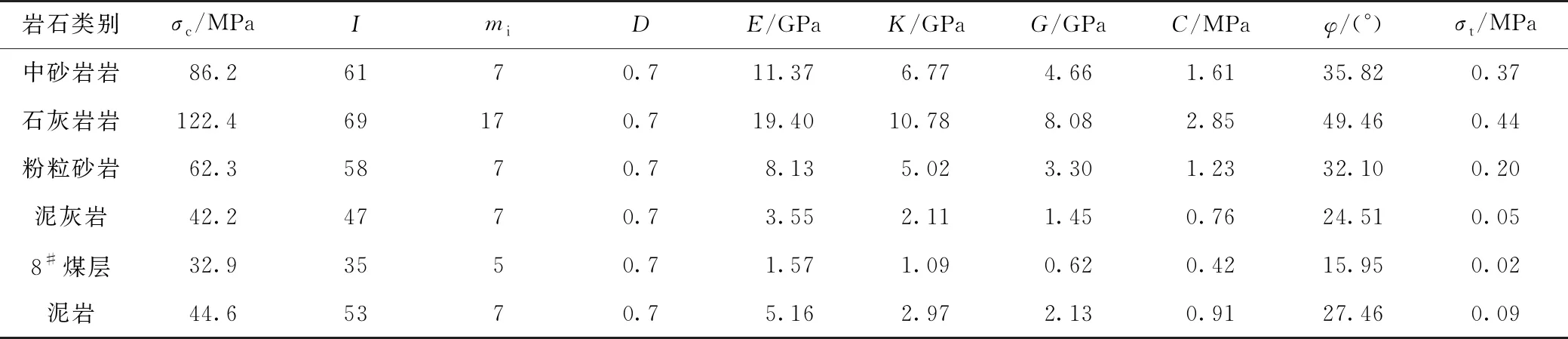
表1 岩体的物理力学特性参数

3 数值模型的建立

根据N8205工作面平面位置关系及对应的钻孔柱状图，采用FLAC3D软件[13-14]建立三维数值模型，如图3所示。模型沿倾向横截面的尺寸为200 m×80 m(长×高)，沿空巷道横截面的尺寸为4.8 m×3.5 m(宽×高)。

图3 三维数值模型沿倾向横截面模型图

由图3可知，模型中侧面采用水平位移约束，底面采用固定约束，顶面施加等效载荷9.6 MPa，侧压系数根据地应力测试结果取值1.6；模型中岩层采用Mohr-Coulomb本构模型，而充填墙体和N8205采空区矸石本构模型的确定，需通过进一步分析；选用FLAC3D软件自带的锚杆/索结构单元体进行沿空巷道内支护结构体的模拟。沿空巷道顶板和两帮采用ø20 mm×2 400 mm的高强度锚杆，顶板锚杆间排距为850 mm×800 mm，两帮锚杆间排距为750 mm×800 mm。在相邻两排锚杆中间位置安装有高强度锚索，对其采用ø20 mm×1 600 mm的高强度锚杆进行支护，锚杆间排距为900 mm×800 mm。锚杆/索结构单元的力学和几何参数如表2所示。

表2 锚杆/索结构单元参数

3.1 充填墙体本构模型及参数确定

养护时间为7 d的试件在实验室测试的应力—应变曲线如图4所示。

图4 试件模拟与实验室测试应力—应变曲线对比

由图4可以看出，当试件的单轴抗压强度达到11.06 MPa峰值应力时，其对应的应变仅为1.7%，随后试件抗压强度衰减，在应变为5.4%时峰后残余应力保持为4.73 MPa，为峰值应力的42.7%。这表明养护时间为7 d的充填墙体有良好的塑性，其具有强度增长速率快、残余强度高等优点，以及显著的应变软化特征。

如图4所示数值模型中对充填墙体采用应变—软化本构模型[15]，且为了获得模型的最优参数，建立标准试件模型，并在试件模型两端面施加相向的恒定速率v，以形成压缩载荷。试件模拟材料参数中体积模量、切变模量和密度分别设定为1.18 GPa、0.26 GPa、1 100 kg/m3，而黏聚力和内摩擦角通过试错法确定。最终校准后的试件模拟应力—应变曲线与实验室测得的结果匹配度较高(见图4)。校准后的黏聚力和内摩擦角数据如表3所示。

表3 黏聚力和内摩擦角随应变变化数据

3.2 N8205采空区矸石本构模型及参数确定

由于覆岩对采空区矸石的压实作用，其会在压实过程中表现出应变硬化的特性。在此用双屈服本构模型对采空区矸石进行建模，以模拟随着采空区体积的逐渐压缩，采空区矸石的支承能力逐渐增大的实际情况。覆岩对采空区矸石的压实过程可由Salamon提出的经验公式[16-17]计算得到：

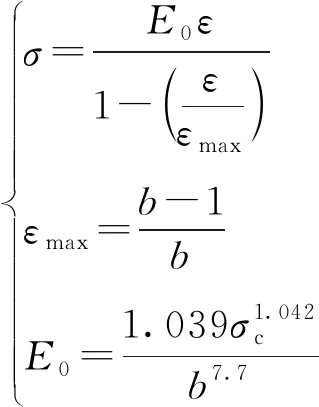
(8)

式中：σ为覆岩对采空区矸石施加的载荷，MPa；E0为初始切线模量，MPa；ε为采空区矸石体积应变；εmax为采空区矸石最大体积应变；b为采空区矸石碎胀系数。

对于N8205采空区，σc和b分别取值为27 MPa和1.23，代入式(8)可以计算得到εmax和E0分别为0.19和65.44 MPa，进而得到理论计算的载荷σ与应变ε之间的关系。采空区矸石数值模型参数的确定可通过建立尺寸为1 m×1 m×1 m的单元子模型，并在模型上表面施加恒定速率v来模拟覆岩加载效应。通过试错法使其应力—应变曲线与理论计算结果匹配度较高，单元子模型模拟与理论计算应力—应变曲线对比如图5所示。

校准后的双屈服本构模型赋值参数如表4 所示。

3.3 数值模型合理性验证

对赋值后的三维数值模型进行运算，并监测了侧向支承应力分布情况，得到N8205采空区侧向支承应力分布曲线如图6所示。

图5 单元子模型模拟与理论计算应力—应变对比曲线

表4 采空区矸石的物理力学特性参数

图6 N8205采空区侧向支承应力分布曲线

由图6可知，在距采空区边缘87 m处支承应力趋于稳定，约为9.54 MPa，即在工作面埋深(430 m)的20.2%位置恢复至原岩应力(10.5 MPa)的91%，该模拟结果与Wilson教授[18]基于大量现场调查和分析所得结论相吻合。

将数值模拟得到的轨道平巷围岩变形量与现场监测结果进行比较，得到的数值模拟与现场监测沿空巷道围岩变形量对比曲线如图7所示。

图7 数值模拟与现场监测沿空巷道围岩变形量对比曲线

由图7可知，数值模拟和现场监测的顶底板最大移近量分别为268、249 mm，数值模拟和现场监测的两帮最大移近量分别为235、225 mm，两者误差均较小，表明所建的三维数值模型较为合理。

4 数值模拟结果分析

4.1 锚杆/索轴向力分析

在不同充填墙体宽度条件下，1#～4#锚杆和5#～7#锚索的最大轴向力变化如表5所示。

表5 不同充填墙体宽度时锚杆/索轴向力变化

由表5可知，实体煤帮侧锚杆的最大轴向力基本保持不变，约为113.0 kN左右，小于其临界轴向力 130 kN。对于顶板中2#和3#锚杆，当充填墙体宽度在2.0 m及其以下时，其轴向力大于其临界轴向力130 kN；当充填墙体宽度大于2.0 m时，随着顶板自身承载能力提高，其轴向力逐渐减小；相反，充填墙体中的4#锚杆轴向力显著提高；对于5#～7#锚索，其轴向力基本随着充填墙体宽度增大而减小，且与5#锚索相比，6#和7#锚索的轴向力变化较大。

综上分析可知，当充填墙体宽度大于2.0 m时，沿空巷道围岩中支护体结构才能完全发挥支护功效；随着充填墙体宽度的继续增大，充填墙体中锚杆的支护轴向力也相应增大。

4.2 沿空巷道围岩变形分析

不同充填墙体宽度条件下沿空巷道围岩变形量曲线如图8所示。

图8 不同充填墙体宽度条件下围岩变形量曲线

由图8可知，顶板岩层变形量最大，充填墙体变形量次之，底板和实体煤帮变形量最小。随着充填墙体宽度增大，围岩变形量均有不同程度下降。当充填墙体宽度从1.0 m增加到2.0 m时，围岩变形较大，此时由于出现严重的顶板下沉和帮部凸出，巷道剩余横截面面积仅为7.8～8.9 m2，小于试验现场有效瓦斯排放临界横截面面积9.0 m2；当充填墙体宽度超过2.0 m时，围岩变形量较小，巷道剩余横截面面积满足试验现场有效瓦斯排放需求[19-20]。

4.3 沿空巷道围岩塑性区分析

不同充填墙体宽度条件下沿空巷道围岩塑性区分布云图如图9所示。

图9 不同充填墙体宽度条件下围岩塑性区分布云图

由图9可知，当充填墙体宽度在2.0 m及其以下时，随着充填墙体宽度的增大，围岩塑性区减小的幅度较大。这是因为随着充填墙体宽度增大，充填墙体承载能力也相应增大，进而显著减小顶板的下沉量，从而使塑性区范围发生明显变化；当充填墙体宽度大于2.5 m时，围岩变形量基本趋于稳定，充填墙体宽度的增大对减小顶板下沉量的影响不明显，因此围岩塑性区发育程度基本不变。

综上分析可知，为了获得一个围岩控制较好的沿空巷道，充填墙体应具有一定的承载能力，同时大部分顶板载荷应由实体煤帮承载。显然，当充填墙体宽度为2.5 m时，其具有一定的承载能力，可以承受部分顶板载荷，而大部分顶板载荷转移至实体煤帮侧，此时沿空巷道处于相对较低的应力环境中。因此，最佳充填墙体设计宽度为2.5 m。

5 现场矿压观测

为了评价留设宽度2.5 m充填墙体时沿空巷道围岩的稳定性，特设置3个间距为20 m的测站(见图1中1#～3#测站)对沿空巷道围岩变形量和承载力进行监测，沿空巷道围岩矿压观测曲线如图10 所示。

图10 沿空巷道围岩矿压观测曲线

由图10可知，在测站超前回采工作面约30 m处，巷道表面移近量开始迅速增加，直至测站滞后工作面60 m处；当测站滞后回采工作面 80 m 时，巷道表面移近量趋于稳定。最终顶底板和两帮移近量分别为636、545 mm，剩余横截断面面积约为10 m2，此断面能够满足试验现场的瓦斯抽放和回风要求；在回采工作面后方20 m范围内，充填墙体的承载力以平均每天0.25 MPa的速度缓慢增加；在回采工作面后方20～35 m内，充填墙体的承载力以平均每天1.10 MPa的速度显著增加；在回采工作面后方35 m范围外，充填墙体的承载力缓慢下降，并稳定保持在8.60 MPa左右，小于其峰值强度11.06 MPa。