基于熵值赋权-改进多层次模糊风险评价在深基坑的应用*

2021-05-10张世民朱小军

佳木斯大学学报（自然科学版） 2021年2期

张世民，付开 , 刘丹，郭帅，朱小军

(1.浙大城市学院土木工程系，浙江杭州 310015；2.绍兴文理学院土木工程学院，浙江绍兴 312000；3.杭州华蕴基础工程有限公司，浙江杭州 310015;4.杭州萧山经济技术开发区建设发展有限公司, 浙江杭州 310015)

0 引言

由于地下空间和高层建筑的发展，基坑发展走向“高、大、深”[1]。同时，基坑工程安全储备小，影响因素多、风险高，尤其是城市基坑，稍有不慎就会引起事故造成重大损失，因此如何对基坑工程进行风险预防和控制，日益成为人们关注的焦点[2]。然而，风险评价是一个多因素、多指标、多层次的过程，数据资料偏差、评价指标不科学、影响因素只可定性描述等使得基坑风险评价具有极大的模糊性和不确定性[3]。吴荣良[4]等人利用模糊评价分析了基坑开挖对周边环境的风险影响；李立云[5,6]、刘政[7]成功运用改进的层次分析对某基坑进行安全风险评价；刘建华[8]等人针对船闸引航道基坑施工的复杂性，结合了层次分析和模糊评价并成功运用在风险评估中。上述评价研究均取得了不错的效果，但都存在着指标权重的确定受主观因素影响大等缺陷，采用对传统的AHP改进，形成IAHP，并和EVM组合赋权确定指标的权重，然后结合多层次Fuzzy理论，对粘土地层深基坑施工风险进行模糊评价，依据结果指导实际工程。

1 风险评价模型指标体系构建

1.1 工程案例背景

铁路北站单元GS1104-18地块中学及社会停车库工程位于杭州市拱墅区，拟建场地地貌单元属于湖沼相沉积地带平原区，地势平缓，地形起伏不大。东侧为新建小区，南侧为新建安置房，西侧为SOHO创意园，北侧为社区服务中心及居民楼。

项目总用地面积42300m2，地上建筑8幢；地下室1层(最大挖深约6m)，均为框架结构。工程围护体系采用PC工法桩+砼支撑的形式，工程桩采用钻孔灌注桩。

根据地勘报告，基坑开挖时主要涉及：①层杂填土,②层粉质粘土、夹粘质粉土，④层淤泥质粘土,局部⑤-1 层粉质粘土和局部⑤-2 层粉质粘土夹粘质粉土。基坑开挖深度较大，同时周边有市政设施，地下管线较多，地下水丰富，埋深在地表下0.60～5.70m 左右，受附近地表径流影响大。

1.2 评价体系的构成及其隶属度

建立评价指标体系是进行风险评价的基础，评价结果的准确性受体系中定量化、定性化的因素影响、制约[9]。考虑所有的影响因素显然不现实，指标过多则计算复杂，过少则会造成较大误差，遵循可测性、代表性和可比性三原则，选择最能表征基坑施工风险的4类16项指标进行分析。

数据来源于问卷调查。调查对象为深基坑专业相关人员，调查周期为2019年11月到12月，发放问卷230份，回收213份，有效问卷196份，有效率为85.22%。通过问卷整理计算各指标评价构成比，如表1所示。

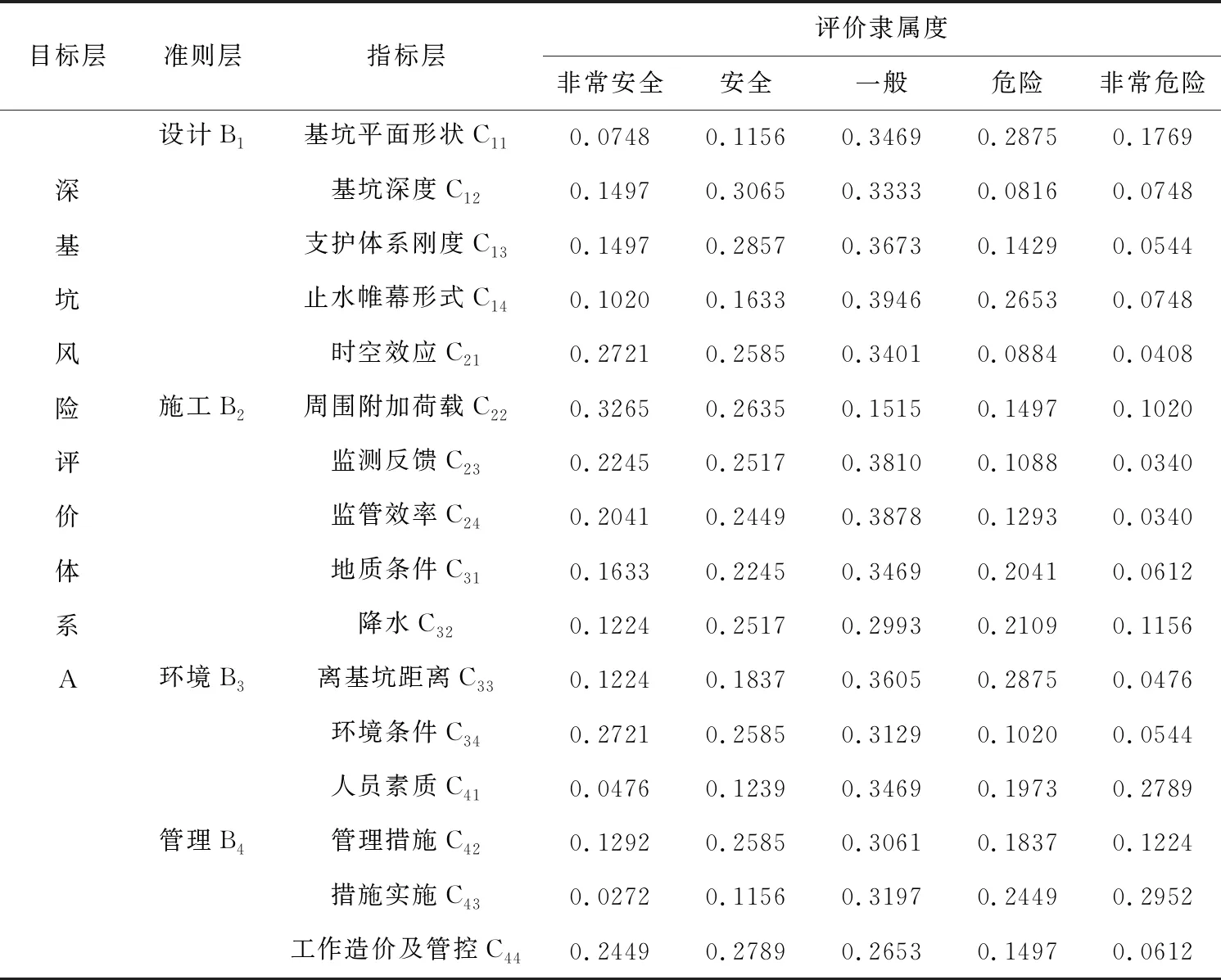
表1 评价指标构成及专家对各指标评价构成比(隶属矩阵)

2 评价指标权重确定

由于模糊数学理论无法确定复杂的指标权重；需计算各指标的权重，当评价指标样本较多时计算量极大[10]。为了保证权重确定的科学性，简化计算，提高风险评价的准确性，结合IAHP和EVM，将主客观赋值法结合起来，通过组合赋权确定指标权重。

2.1 改进的AHP法

AHP[11]是一种定性兼定量的多目标分析方法，能够条理化和层次化复杂系统的各因素，定量表示每一层次的相对重要性，并用数学方法确定表达各因素相对重要次序的权值[12]。由于其内部矛盾可通过一致性检验来避免，进而保障群体决策的一致性，因此在土木工程领域广泛应用[13-14]。采用三标度改进AHP，并对指标赋权，步骤如下[15]：

(1)构造各层次比较矩阵P和判断矩阵A

比较矩阵的建立是通过该级指标两两比较其上一层级的重要程度而来，公式如下：

(1)

根据三标度法，其中：

(2)

生成比较矩阵P之后可构造出相应的判断矩阵A=[aij]m×n，其中：

(3)

(2)评价指标权重计算

首先利用公式(4)计算各指标的权重，再由公式(5)对权重作归一化处理：

(4)

(5)

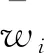
根据评分结果，采用三标度法计算得到各层次指标的判断矩阵，并计算最终指标权重,结果见表2。

表2 评价体系各指标IAHP权重

该表标度采用三标度法，在指标两两比较时只能在0-2三个数字中选择，选择更为可靠和简便，克服了传统标度法对指标标度刻划过多，导致专家评价存在片面性和差异性从而影响指标权重不够准确的缺陷。

2.2 EVM法

随着评价要求的提高，AHP的缺陷逐渐凸显，权重的确定依赖主观评价影响评价的科学性[17-19]。熵值法赋权客观，可以修正AHP主观赋权的不足，提高赋权的科学性。EVM赋权步骤如下：

(1)计算指标比重

依据评价隶属度，构成m指标n个对象的初始数据矩阵X=[xij]m×n，依照公式(6)得到指标值xij在第j项指标值所占的比重：

(6)

(2)计算第j项指标的熵值、效用值

熵值：

(7)

效用值：

(8)

(3)计算第j项指标的权重

通过公式(6)至(8)，可以得到评价指标体系各指标的权重，见表3。

表3 评价体系各指标EVM权重

通过EVM获得的指标权重是一种客观权重，不受人为主观因素的影响，但另一方面无法有效利用专家评判信息，导致权重构成机械化。

2.3 IAHP+EVM组合赋权

为了充分利用主观赋权的有效信息和客观赋权的公正性，结合 IAHP+EVM进行组合赋权，确定综合指标权重W：

(9)

其中：t根据经验一般取0.5。

通过组合赋权，最终形成深基坑风险评价的指标体系综合权重值，见表4。

通过IAHP+EVM的组合赋权，既有效利用专家的判断结果，又发挥了技术评价的客观性，使得到的指标权重更加合理。

3 基坑风险的模糊综合评价

Fuzzy是模糊性问题评价研究的常用数学工具，它的应用为基坑风险评价中那些只能定性描述的模糊概念、判断的数字化、定量化提供了理论依据[20]，不仅考虑了基坑施工过程的渐变性和模糊性，也考虑了影响因素的多面性。由于复杂事物的评判要涉及的因素很多且为不同层次，一级Fuzzy评价会泯灭大量单因素判断信息，使得评价丧失意义。因此采用二级Fuzzy评价。