断续结构面岩质边坡的应力敏感性分析
2021-05-09张志勇宋之恒余化彪胡朝赟聂正一
张志勇,宋之恒,余化彪,胡朝赟,聂正一
(云南省建设投资控股集团有限公司,云南 大理 671000)
0 引言
我国公路、铁路、水利等基础设施建设不可避免开挖大量的岩质边坡,岩质边坡中结构面的存在极大削弱其稳定性,使边坡的破坏更具有突发性。为了边坡的防灾、减灾及治灾,避免不必要的损失,有必要开展结构面岩质边坡监测预警研究。
断续结构面岩体以块体移动方式失稳时,首先是原有结构面扩展,生成新裂面,进而使原有结构面相互连通,构成统一的失稳分离面。近年来,诸多学者[1-11]开展了结构面岩质边坡监测的理论分析、模型试验及数值模拟研究。其中,尤春安[3]采用明德林解推导出全长黏结锚杆在拉拔力作用下锚杆轴力和剪应力的数学解析解,证实全长黏结锚杆能够准确的传递出边坡内部应力场的变化,是应力监测的良好载体;朱训国[5]基于Boussinesq位移解,推导出与尤春安教授相同的锚杆应力解析解数学表达式。在离心模型试验研究中,姚裕春等[6]进行离心模型试验,采用在小钢片贴应变计的方法监测边坡内部应力变化,来反应不同开挖支护时机对边坡稳定性的影响;杨明等[7]对斜坡堆积体的抗震防护措施进行研究,发现锚杆可以改善坡体内部的应力调整规律,能极大地减小地震作用下边坡坡面变形以及改善抗滑桩受力状态;郭永建[8]提出运用全长黏结锚杆作为“媒介”来反应坡体内应力调整,从而对岩质边坡的稳定状况进行预警;采用全长黏结锚杆对岩质边坡破坏过程中内部应力场的变化进行研究,得出岩质边坡应力敏感部位;晏长根等[9]开展均质岩质边坡离心模型试验,研究了锚杆的应力响应规律。在数值模拟分析中,廖小平等[10]对全长黏结式预应力锚杆进行数值模拟和现场实验,得出全长黏结式预应力锚杆能够在预应力损失的前提下,能保持较高的预应力水平;何忠明[11]采用FLAC3D进行加锚情况下顺倾向岩质边坡的数值分析,结果表明:全长黏结锚杆的轴力分布函数是一条多峰值曲线,且锚杆轴力最大值均位于结构面处,证实锚杆轴力最敏感部位处于滑动面位置。学者们对于均质岩的边坡研究较多,而在实际应用和生活中,由于自然界的不确定因素,非均质岩的边坡研究就显得尤为重要。
本文在总结前人研究成果的基础上,以锚杆为测力媒介进行了三组结构面分布形式不同的断续结构面岩质边坡离心模型试验,并用 FLAC3D软件进行数值模拟,以探讨三种断续结构面应力敏感部位,研究成果可为断续结构面岩质边坡锚杆应力监测的推广应用提供参考。
1 边坡离心模型试验方案
1.1 材料选择及制作
模型试验采用TLJ-3土工离心试验机,最大容量为 60 g-t,最大离心加速度为200 g,有效半径为 2.0 m,模型箱长×宽×高为500 mm×360 mm×400 mm。该试验是将土工模型置于高速旋转的离心机中,让模型承受离心加速度(大于重力加速度),补偿因模型缩尺带来的自重损失,更接近于实际。边坡模型材料按照石英砂∶重晶石粉∶石膏粉∶水=1∶1∶0.3∶0.42 的比例配制模拟软岩[12-14],通过试验确定边坡模型材料的物理力学参数见表1。模型采用填筑法制作,在模型箱内侧均匀涂抹凡士林以尽量消除边界摩阻效应,填筑至结构面时铺设裁好的塑料纸模拟结构面,经直剪试验测得厚塑料纸内摩擦角为29°,黏聚力为5 kPa。采用熟铁片模拟全长黏接锚杆,横截面积为 8 mm(宽)×1 mm(厚),长10 cm,弹性模量约为200 GPa,上部贴设120-3AA无端子免焊接电阻应变计进行应力监测,模型加工时预留锚杆注浆孔道,采用超细水泥浆作为锚杆黏接剂[12]。
1.2 试验设计
本文共设计三种不同断续结构面岩质边坡应力监测模型(图1),三种模型中断续结构面贯通率均为50%,结构面倾角为49°。模型A设有2组沿在同一条直线分布的结构面,模型B设有3组沿同一条直线分布的结构面,模型C设有2组平行分布结构面。沿模型坡面自上而下依次布置1号、2号、3号锚杆,锚杆间距为90 mm。1号锚杆布设监测点1、2、3,2号锚杆布设监测点4、5、6,3号锚杆布设监测点7、8、9。各监测点布设原则:1、4、7监测点距离锚杆端头20 mm,2、5、8监测点距离锚杆端头50 mm,3、6、9监测点距离锚杆端头80 mm,同时适当调整位置以保证监测点布置在结构面处。

图1 三种断续结构面边坡模型

图2 三种断续结构面边坡模型实物图
1.3 试验加载
试验中采用分级加速方法,离心加速度按每级提升20 g,模型A、B、C离心加速时间见表2。

表 2 三种模型(A,B,C)的离心加速时间
1.4 数据收集
离心机可实时监控并传输试验过程中锚杆的应变数据,根据胡克定律可计算锚杆的应力值。由于工程上主要以轴力描述锚杆的受拉状态,通过公式F=n2EζA模(F为轴力,n为离心加速度,E为锚杆弹性模量,ζ为锚杆应变,A模为锚杆截面积)将应力值换算为轴力值。
2 试验结果分析
2.1 试验现象
试验加载至约120 g时,各边坡模型发生破坏,试验破坏侧视图见图3。由图3a可知,边坡模型A破坏时滑动面为直线型,开挖边坡发现监测锚杆均被压弯,上部锚杆弯折幅度较小,中下部锚杆弯折幅度较大。由图3b可知,边坡模型B产生近似圆弧型滑动,开挖边坡发现上部监测锚杆被拔出且有小幅弯折,中下部锚杆被压弯。由图3c可知,边坡模型C破坏时滑动面近似“S”型,开挖边坡发现,中上部锚杆大幅度弯折,下部锚杆弯折幅度较小。

图3 三种模型的边坡破坏侧视图
2.2 锚杆监测结果分析
模型A各监测点轴力历时曲线见图4。由图4可知,在660 s之前,监测点1、2、3轴力值为负,锚杆1为受压状态,监测点4、5、6、7、8、9轴力值为正,锚杆2、3为受拉状态。监测点7约480 s时产生明显应力响应,其他监测点在700~900 s时产生明显应力响应。在900~1620 s,监测点3、5、7分别相对于锚杆1、2、3上的其他监测点响应量值及增速更大,则模型A应力敏感区域位于结构面贯通区,且监测点3、5、7位于边坡破坏直线型滑面上,验证模型A试验现象。监测点1~9轴力终值趋于收敛,分别为 41 kN、60 kN、78 kN、52 kN、96 kN、35 kN、103 kN、42 kN、14 kN。监测点5、7的轴力增长速率及轴力终值均大于监测点3,说明模型A中下部比上部更为敏感,但监测点5、7的轴力增长速率较为相近,下文采用数值模拟分析模型A最敏感部位。

图4 模型A监测点轴力-时间变化曲线
模型B各监测点轴力历时曲线见图5。由图5可知,在360 s之前,锚杆1、2、3为受压状态,边坡相对稳定。监测点7约在540 s时产生明显应力响应,其他监测点在800~900 s时产生明显应力响应。在900~1610 s时,监测点2、5、7分别相对于锚杆1、2、3上的其他监测点响应量值及增速更大,证明模型B应力敏感区域位于潜在滑动面处,且监测点2、5、7位于边坡破坏圆弧滑面上,验证模型B试验现象。监测点1~9轴力终值趋于收敛,分别为42 kN、78 kN、45 kN、54 kN、97 kN、80 kN、106 kN、88 kN、31 kN。监测点5/7的轴力增长速率及轴力终值均大于监测点2,同时监测点8监测量值及变化速率也较大,综合分析模型B应力最敏感位置在靠近边坡下部坡脚剪出口。
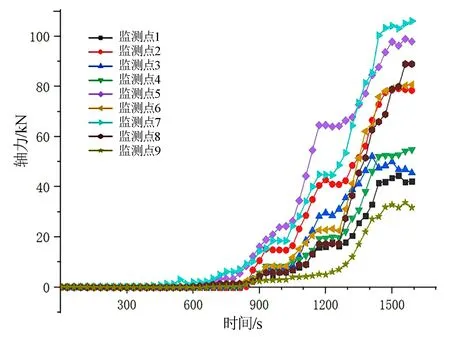
图5 模型B监测点轴力-时间变化曲线
模型C各监测点轴力历时曲线见图6。由图6可知,在加速之后,各监测点轴力值均为正值,锚杆1、2、3为受拉状态,边坡产生相对滑动趋势。监测点2、4、5、7约500 s产生明显应力响应,其他监测点在600~800s时产生明显应力响应。在800~1640 s时,监测点2、7分别相对于锚杆1、3上的其他监测点响应量值及增速更大;监测点4、5对边坡内部应力调整均较为敏感,可推测2号锚杆轴力最大值位于监测点4、5之间。综合监测点2、4、5、7监测数据,模型C应力敏感区域位于结构面贯通区,同时可验证模型C试验现象。监测点1~9轴力终值趋于收敛,分别为45 kN、105 kN、33 kN、65 kN、85 kN、35 kN、96 kN、47 kN、18 kN。监测点2轴力增长速率及轴力终值均大于其他监测点,则模型C应力最敏感部位位于结构面贯通区上部。

图6 模型C监测点轴力-时间变化曲线
3 FLAC3D数值模拟
3.1 模型建立与参数选取
岩体本构关系采用莫尔-库伦模型,边界条件采用将构造应力作为安全储备的位移边界条件,模型网格划分主要采用六面体单元,局部采用四面体单元;单元划分时主要在潜在滑体以及全长黏结锚杆位置处加密,其他位置相对较大[15-16]。
根据模拟相似材料物理力学参数,参照我国相关规范[17]附录D对工程岩体物理力学参数的建议,选取泊松比为0.3。采用弹性求解法生成数值模型初始地应力,然后采用莫尔-库伦本构模型进行计算,可得出摩尔库伦模型中的
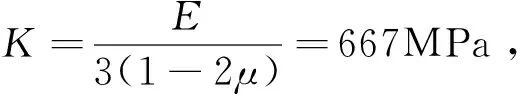

结构面采用 FLAC3D中的 interface 接触面单元进行模拟,interface参数见表3。锚杆入射角为18°,直径为22 mm,长度取10 m,钻孔直径取75 mm,采用cable单元模拟,取cable单元物理力学参数表见表4。

表3 Interface 参数

表4 Cable 单元参数
3.2 数值模拟结果分析
提取各模型锚杆监测点在不同重力加速度下锚杆轴力数据并绘制监测点-轴力加速度曲线图,在重力加速度为1.2 g的情况下边坡的剪应变增量云图(对应于边坡在120 g离心加速度情况边坡发生失稳破坏的状态)见图7b、图8b、图9b,锚杆各监测点在不同重力加速度下锚杆轴力数据并绘制监测点-轴力加速度曲线,见图7a、图8a、图9a。
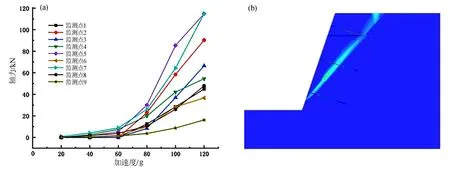
图7 模型A监测点轴力-加速度曲线(a)与模型A应变增量云图和锚杆轴力分布云图(b)

图8 模型B监测点轴力-加速度曲线(a)与模型B应变增量云图和锚杆轴力分布云图(b)
由图7a可知,3、5、7号监测点曲线增长速度和变化量值均远大于同锚杆其他监测点,且由图7b可知,模型A边坡最大剪应变增量位于潜在的结构面贯通区,证实离心试验中模型A敏感区域位于潜在的结构面贯通区。5、7号监测点的轴力最大值相近,但在离心加速度为80 g~100 g 时,5号监测点轴力值比7号监测点变化速率快,应力响应更为敏感,故模型A的应力最敏感部位位于潜在结构面贯通区的中部。
由图8a可知,2、5、7号监测点曲线增长速度和变化量值均远大于同锚杆其他监测点,且由图8b可知,模型B边坡最大剪应变增量呈现圆弧形,证实模型B离心试验产生类似的圆弧形滑动,敏感区域位于2、5、7号监测点构成的潜在圆弧滑面。在离心加速度为80 g~100 g时,7号监测点轴力值比5号监测点变化速率快,应力响应更为敏感,故模型B的应力最敏感部位位于坡脚部位。
由图9a可知,2、7号监测点曲线增长速度和变化量值均远大于同锚杆其他监测点,且由图9b可知,模型C边坡最大剪应变增量位于潜在的结构面贯通区,证实模型试验中模型C敏感区域位于潜在的结构面贯通区。4、5号监测点数据均比较大,侧面反映边坡在锚杆2的4、5监测点之间产生贯通区。在离心加速度为80 g~100 g时,2号监测点轴力值比7号监测点变化速率快,应力响应更为敏感,故模型C的应力最敏感部位位于潜在结构面贯通区的上部。
4 结论
本文利用离心模型试验和数值方法对岩质边坡三种断续结构面的分布形式进行模拟,通过两种不同的方法得到的结果能互相印证综合对比得出以下结论:
1)在贯通率都为50%的情况下,断续结构面的不同分布形式对边坡的稳定性及边坡破坏模式产生较大影响。边坡模型A破坏时滑动面为直线型,边坡模型B破坏时产生近似圆弧型滑动,边坡模型C破坏时滑动面近似“S”型。
2)随着离心加速度的增大,大部分监测点轴力值呈现阶梯式增长趋势。模型A的7号监测点在1620 s时产生轴力最大值为103.34 kN,模型B的7号监测点在1560 s时产生轴力最大值为106.09 kN,模型C的2号监测点在1620 s时产生轴力最大值为105.63 kN。
3)断续结构面的不同分布形式影响边坡内部应力场调整,边坡模型A应力敏感区域位于结构面贯通区,且结构面贯通区中部的应力最敏感;边坡模型B应力敏感区域位于潜在滑动面处,且滑动面坡脚剪出口处应力最敏感;边坡模型C应力敏感区域位于结构面贯通区,且结构面贯通区上部的应力最敏感。
