非赫兹型滚滑接触荷载作用下钢轨体内应力状态模拟分析

王攀杰 周佳仪 孙耀亮 李粮余 安博洋 王平

（1.西南交通大学高速铁路线路工程教育部重点实验室，成都 610031；2.西南交通大学土木工程学院，成都 610031；3.中铁二院工程集团有限责任公司，成都 610031）

铁路运营过程中，轮轨滚动接触疲劳损伤现象十分普遍，可以分为三类［1]：由表面伤损直接形成；在钢轨次表层形成；由于踏面以下深处存在材料缺陷而形成。其中由钢轨次表层形成的滚动接触疲劳是由于轮轨匹配时过高的应力水平和蠕滑程度联合局部较低的抗疲劳性能，在钢轨次表层产生应力集中，形成高周滚动接触疲劳［2]。

以往钢轨体内应力状态模拟研究中大多采用赫兹接触理论对轮轨荷载进行简化处理，并假定轮轨处于全滑动状态，著名的安定理论正是基于该假设提出的［3]。文献［4]考虑轮轨接触全滑动状态建立了赫兹椭圆接触模型，发现当摩擦因数小于0.33 时最大von Mises 应力的位置不会出现在钢轨表层。文献［5]进行了赫兹载荷轮轨接触全滑动状态作用下von Mises半无限空间的安定性研究，发现当摩擦因数较小时最大von Mises 应力发生在钢轨表面以下，随着摩擦因数逐渐增大到0.3，其位置逐渐上移到表面。文献［6]基于赫兹椭圆接触模型分析了三种蠕滑状态下钢轨体内的残余应力和变形。文献［7]采用赫兹椭圆接触荷载在不同蠕滑状态下进行了摩擦因数的参数化分析。文献［8]基于半空间求解方法，对Love［9]的方法进行了改进，求解赫兹椭圆接触荷载下的次表层应力。

实际的轮轨滚动接触往往处于非赫兹型接触荷载+部分滑动状态。文献［10]对比了S1002，S1002CN踏面与UIC60 轨面匹配时的接触斑，发现非赫兹接触斑与赫兹接触斑具有较大的差异。因此，采用赫兹型接触荷载+全滑动状态进行疲劳预测会引起一定的计算误差，且其影响尚不明确。因此，有必要采用更接近真实轮轨接触状态的模型模拟钢轨体内表层的应力状态，并探究接触载荷状态对疲劳预测的影响。

本文基于半空间求解方法，考虑摩擦因数和蠕滑状态两个影响因素，综合研究赫兹型和非赫兹型两种接触荷载作用下轮轨滚动接触模型中钢轨体内应力分布特性，并对比赫兹型接触荷载+全滑动状态（简称赫兹型全滑状态）和非赫兹型接触荷载+部分滑动状态（简称非赫兹型部分滑状态）这两种轮轨滚动接触状态的钢轨体内应力和塑性变形累积情况。

1 计算方法

模拟钢轨体内应力状态时，先求解钢轨表层接触应力作为钢轨体内应力计算的输入量，然后基于半空间求解的计算原理完成钢轨体内应力的计算。

1.1 求解表层接触应力

首先计算目标工况的接触几何参数，参照迹线法原理［11]，自编程序求得轮轨匹配的接触点、轮轨接触几何参数等；再借助基于Kalker 的三维非赫兹滚动接触理论中的CONTACT 程序求解钢轨接触区域的表层接触应力，作为求解钢轨体内应力的输入量。

1.2 求解钢轨体内应力

参照Love 的半空间假设计算模型［9]，建立压力作用在半空间表面的固体模型（图1），再通过弹性力学中的经典势函数理论解对物体内任一点的位移解与应力解进行表达。图1中，Oxyz为规定空间坐标系；x，y，z分别为纵向（沿轨道方向）、横向（沿轮轴方向）、垂向（向下为正）；Px，Py，Pz分别为三个方向的表面荷载。

图1 表面载荷作用于半空间表面模型

钢轨内任一点E（x，y，z）到激励点E′（x′，y′，0）的距离r为

为了表示钢轨体内任一点位移场和应力场的一般解析解，定义势函数Q(i)j(i= 0，1，2；j=x，y，z)和辅助势函数ψ(k)(k= 0，1)，其具体表达式参见文献［8]。

E（x，y，z）的弹性位移场δx，δy，δz可以表示为

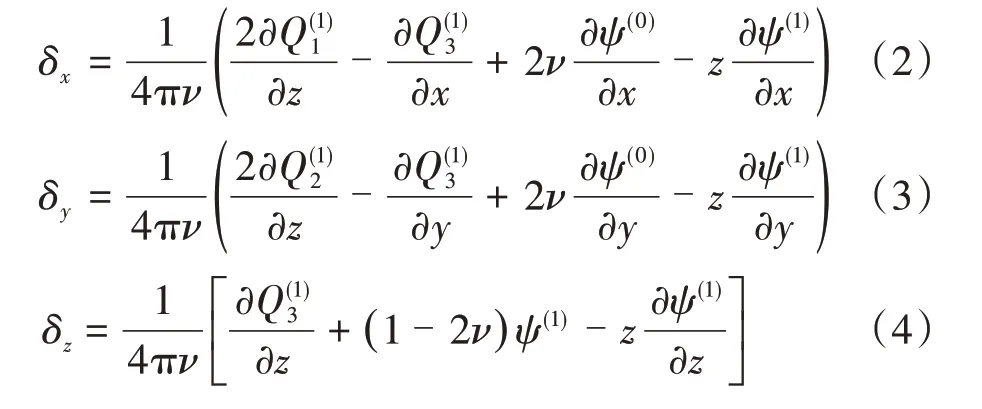
式中：ν为泊松比。

应力场的解σmn(m=x，y，z；n=x，y，z)可以由位移场通过胡克定理求得，其结果可以表示为

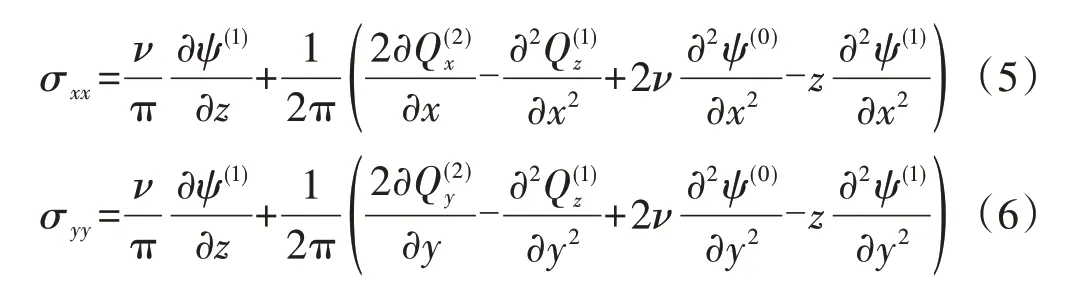
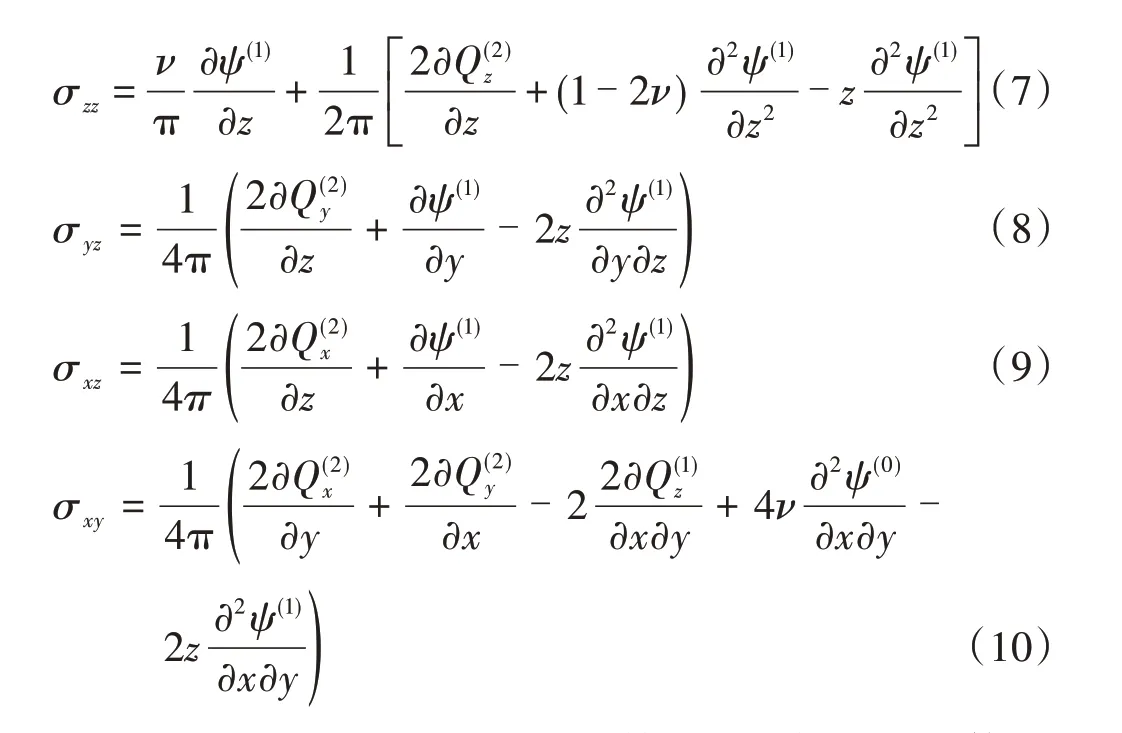
根据式（5）—式（10）的计算结果，求解钢轨体内任一点的von Mises等效应力σvm，即

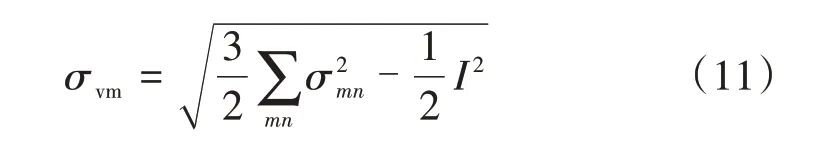
式中：I为应力张量第一不变量，I=σxx+σyy+σzz。

2 表层接触应力分析

选用我国高速铁路典型的S1002CN 车轮踏面［10]和CHN60 钢轨型面［12]，设置1/40 的轨底坡；轮对轴重14 t；轮轨材料的弹性模量为209.92 GPa，剪切模量为82 GPa，泊松比ν= 0.28。

2.1 不同轮对横移量下法向接触应力的求解

针对高速铁路运营时常见的轮轨滚动接触状态，选择轮对横移量w=-3 ～6 mm进行接触计算，其中w的正负分别表示向轮对外侧、内侧横移。利用CONTACT程序求解得到轮对横移量不同时非赫兹型和赫兹型两种接触荷载作用下的接触斑形状和法向应力，结果见图2和表1。图2中自左向右依次对应w=-3，-2，-1，0，1，2，3，4，5，6 mm，图2（a）中黑线表示相同参数下赫兹型接触斑形状。

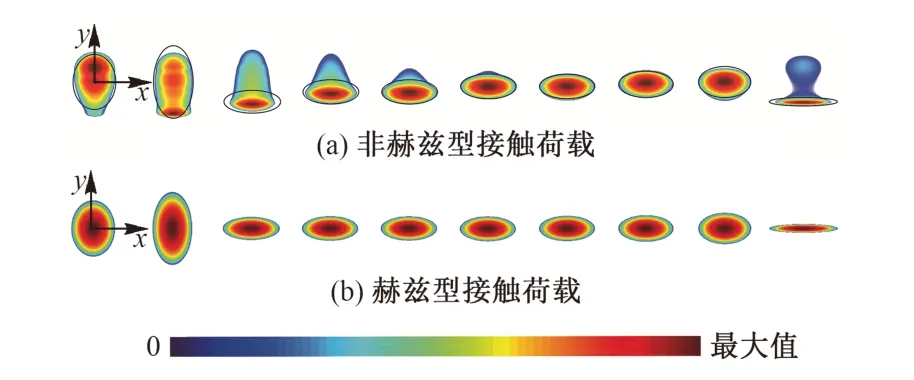
图2 不同轮对横移量时的接触斑形状和法向应力分布

表1 轮对横移量对最大法向应力的影响

从图2 和表1 可知：①w= -3，-2，1，2，3，4，5 mm时，两种接触荷载作用下接触斑外形比较接近，最大法向应力差异不大。②w=-1，0，6 mm时，两种接触荷载作用下接触斑纵向尺寸相近，但非赫兹型的接触斑横向尺寸大于赫兹型，故接触面积大于赫兹型，而最大法向应力小于赫兹型。在w =6 mm 这种恶劣接触工况下，非赫兹型的最大法向应力比赫兹型小25%。

由于接触荷载的不同直接影响接触斑的几何形状，在钢轨体内应力状态模拟分析时，选择两种接触荷载作用下接触斑纵向尺寸相近的w=0 和横向尺寸相近的w=-2 mm这两种轮对横移量工况。

2.2 纵向蠕滑状态对轮轨接触的影响

轮对沿钢轨滚动发生横移或偏转时，轮轨之间在垂直于接触平面的横向、纵向和垂向产生相对位移，这种相对位移被称为蠕滑［13]。蠕滑达到一定程度时，轮轨间接触为全滑动状态，即达到蠕滑饱和［14]。本文只研究纵向蠕滑率ξx对轮轨接触的影响，将横向蠕滑率ξy和自旋蠕滑率ξn都设为0。通过ξx来改变纵向蠕滑力，控制轮轨接触的蠕滑程度。定义同一坐标下纵向牵引系数与摩擦因数的比值为饱和度。饱和度μ取值为0 ～1，μ= 1时即蠕滑饱和状态。μ的表达式为

式中：Fx为纵向力；f为摩擦因数；FN为法向力。

取μ=0.2，0.4，0.6，0.8四种蠕滑状态进行分析。w= 0，-2 mm 时，赫兹型和非赫兹型两种接触荷载作用下接触斑的黏滑分布见图3。图中：自左向右依次为μ= 0.2，0.4，0.6，0.8；红线包裹的是黏着区，其余部分是滑动区。不同饱和度下最大纵向应力见表2。

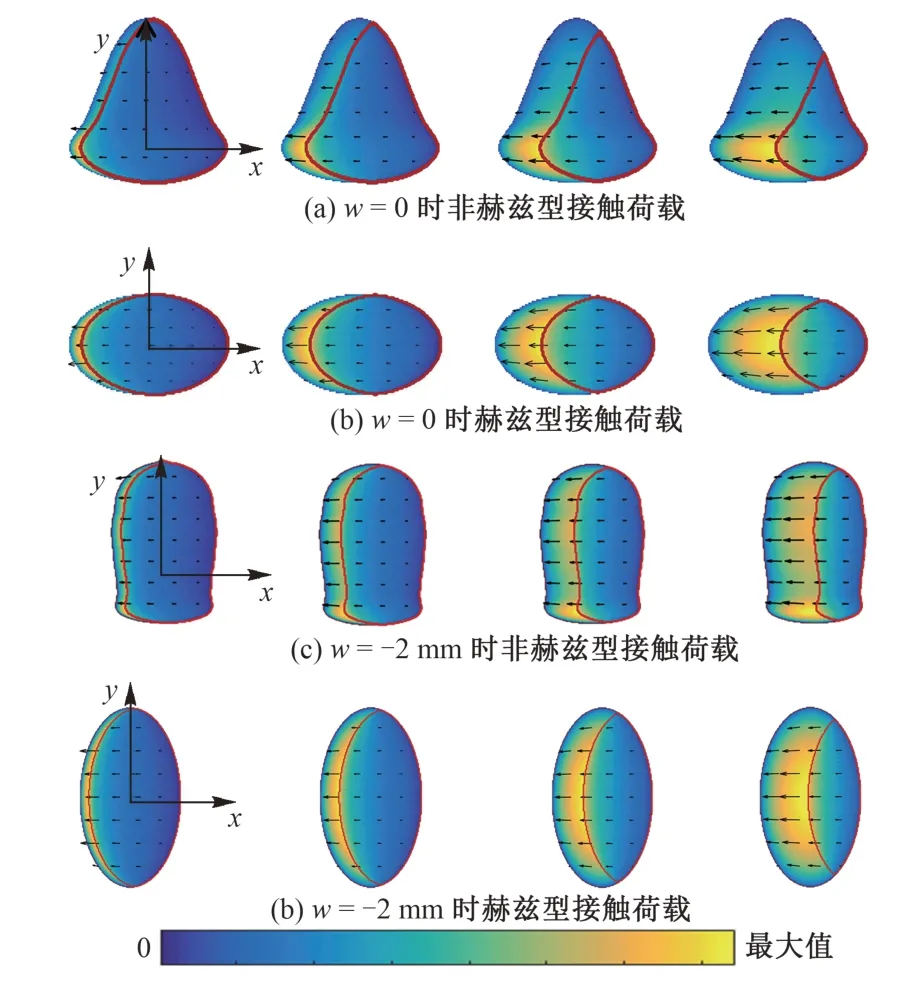
图3 蠕滑状态对接触斑黏滑分布的影响

表2 饱和度对最大纵向应力的影响

由图3 和表2 可知：两种轮对横移量工况下，随着饱和度增大，接触斑滑动区的占比和接触区域中的纵向应力逐渐增大；赫兹型和非赫兹型两种接触荷载作用下的接触斑黏滑分布具有相似的变化规律。

综上，接触斑内黏滑分布和纵向应力整体分布情况主要由饱和度控制，而接触斑的形状不同主要影响着接触斑内的应力水平。

3 钢轨体内应力状态模拟分析

3.1 典型工况下的等效应力分布

以轮轨匹配时典型工况w=0为例，探讨钢轨体内等效应力分布。μ=0.8，f=0.3，0.5时，赫兹型接触荷载作用下钢轨体内von Mises等效应力σvm分布见图4。

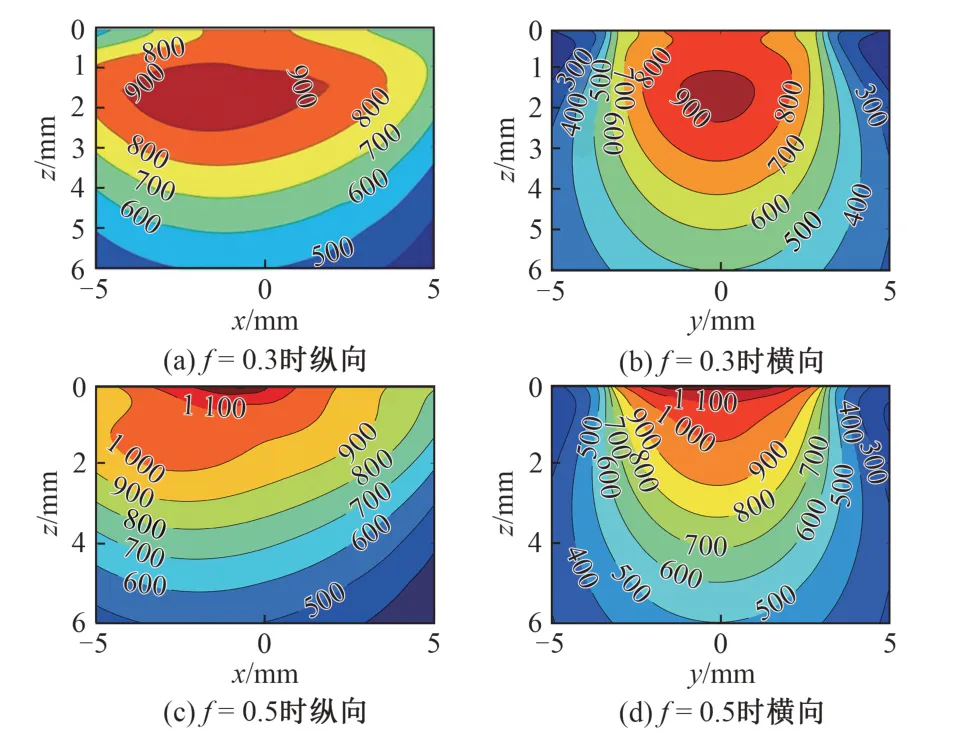
图4 典型工况下钢轨体内等效应力分布（单位：MPa）

由图4可知：f=0.3时，随着深度的增加，σvm先逐渐增大后急剧减小，最大von Mises 等效应力σvm，max发生在次表层；f =0.5 时，σvm随深度增加而线性减小，σvm，max发生在次表层；f=0.5时的σvm，max比f=0.3时增加了30%。

3.2 钢轨体内应力状态参数化分析

从典型工况的研究结果来看，饱和度与摩擦因数的大小都是影响钢轨体内等效应力分布的重要因素，须对钢轨体内等效应力分布做详细的参数化分析，模拟不同蠕滑状态和接触荷载下的钢轨轨体内应力状态，探讨最大von Mises等效应力的分布规律。

3.2.1 蠕滑状态对钢轨体内应力的影响

w=0和w=-2 mm这两种轮对横移量工况下钢轨体内应力的变化规律一致，本文只分析w =0 工况。摩擦因数取f=0.1 ～0.6，在赫兹型接触荷载作用下，计算得到钢轨体内最大von Mises等效应力σvm，max及其出现的垂向位置随饱和度的变化曲线，结果见图5。

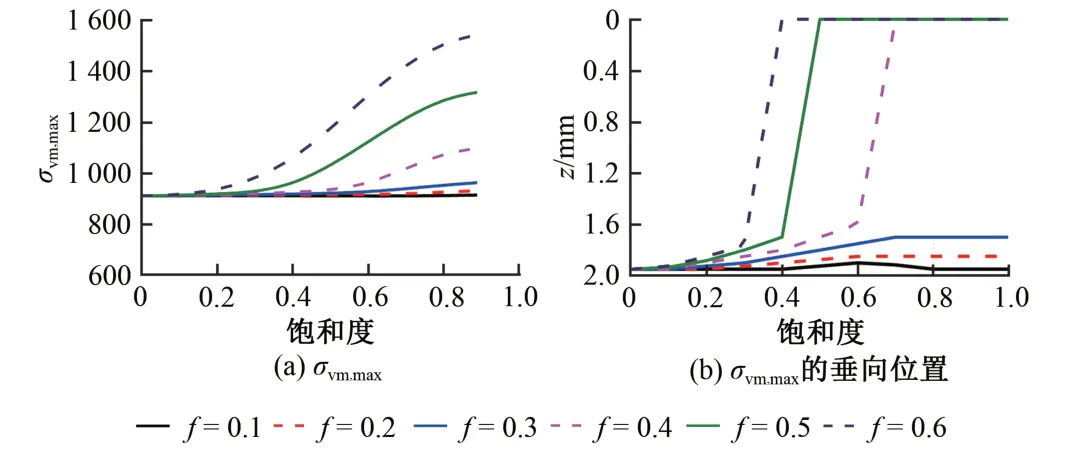
图5 蠕滑状态对钢轨体内应力的影响

由图5 可知，随着饱和度的增大：①对于f=0.1 ～0.6，σvm，max逐渐增大且位置逐渐接近表层。②f≤0.3时σvm，max缓慢增大，与没有蠕滑的状态相比，蠕滑饱和状态的σvm，max增幅在5%以内；f ＞0.3 时σvm，max增幅明显加大，f =0.4，0.5，0.6 时增幅分别为22%，46%，71%。因此，摩擦因数越大，蠕滑饱和时最大von Mises等效应力越大。③f≤0.3时，σvm，max的垂向位置从次表层缓慢向表层移动，至蠕滑饱和时稳定于钢轨下1.6 ～2.0 mm 处；f ＞0.3 时，当饱和度增大到一定程度，σvm，max的垂向位置突升至表层，且摩擦因数越大，跃升至表层所需的饱和度越小。因此，摩擦因数越大，最大von Mises等效应力越容易发生在表层。

3.2.2 接触荷载类型对钢轨体内应力的影响

取w=-3 ～6 mm，轮轨接触状态考虑为全滑动状态即μ=1，计算得到赫兹型和非赫兹这两种接触荷载作用下钢轨体内最大von Mises等效应力σvm，max及其出现的垂向位置随饱和度的变化曲线，见图6。

图6 接触荷载类型对钢轨体内应力的影响

由图6 可知：①对于不同的摩擦因数和轮对横移量，赫兹型接触荷载作用下的最大von Mises 等效应力都略大于非赫兹型，其中w =-1，0，6 mm 时差异较大，这与图2 中两种接触荷载类型的法向应力差异较大相对应。说明同一参数的接触状态下，接触荷载类型对钢轨体内应力水平起着主要影响。②在轮轨接触为全滑动情况下，f=0.3 时所有工况的σvm，max都发生在次表层，而f=0.5 时所有工况的σvm，max都发生在表层。这表明进行轮轨滚动接触计算时，接触荷载类型对钢轨内最大von Mises 等效应力的垂向位置没有影响。

3.3 接触假设的适用性

3.3.1 轮轨滚动接触状态对钢轨体内应力的影响

不考虑摇头角时横向蠕滑率ξy=0。根据文献［15]算得不同横移量下不考虑摇头角的纵向和自旋蠕滑率ξx，ξn（表3），进而算得赫兹型全滑状态和非赫兹型部分滑状态两种轮轨滚动接触状态下钢轨体内最大von Mises 等效应力σvm，max及其出现的垂向位置随轮对横移量的变化曲线，结果见图7。

表3 不同轮对横移量下的纵向和自旋蠕滑率

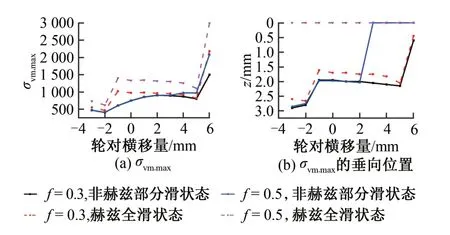
图7 轮轨滚动接触状态对钢轨体内应力的影响

由图7 可知：①对于不同的摩擦因数和轮对横移量，赫兹型全滑状态的最大von Mises 等效应力都大于非赫兹型部分滑状态。其中w=-1 mm 时二者相差最大，在f=0.3，0.5条件下，赫兹型全滑状态的σvm，max分别是非赫兹型部分滑状态的1.7，2.3倍。轮轨滚动接触状态对钢轨体内应力影响较大。②f=0.3条件下，两种轮轨滚动接触状态下σvm，max都发生在次表层，其中赫兹型全滑状态下更接近表面；f=0.5 条件下，赫兹型全滑状态的σvm，max均发生在表层，非赫兹型部分滑状态的σvm，max在w=-3 ～2 mm 时发生在次表层，w=3 ～6 mm时发生在表层。赫兹型全滑动状态时钢轨体内最大von Mises等效应力更易发生在表层。

3.3.2 轮轨滚动接触状态对钢轨体内塑性变形的影响

钢轨体内等效应力大于材料屈服应力时，钢轨体内会产生塑性应变。根据文献［16]计算经过N次荷载冲击累积后两种轮轨滚动接触状态下钢轨体内的塑性变形。计算时取钢轨材料屈服应力为450 MPa，w=0，N=10，20，计算得到沿深度方向的塑性变形曲线，见图8。塑性变形取该深度的最大塑性变形。

图8 轮轨滚动接触状态对钢轨体内塑性变形的影响

由图8可知：对于不同的摩擦因数，随着加载次数的增加，两种轮轨滚动接触状态下钢轨沿深度的塑性变形均显著增加；f=0.3 条件下，两种轮轨滚动接触状态下的最大塑性变形都发生在次表层；f=0.5条件下，非赫兹型部分滑状态的最大塑性变形都发生在次表层，而赫兹型全滑状态的发生在表层，与最大von Mises等效应力位置分布规律相同。

综上，以赫兹型接触荷载+全滑动状态为前提的简化轮轨接触疲劳预测模型（如安定图）在进行轮轨接触疲劳分析时，得到的疲劳预测结果偏于保守。

4 结论

1）接触荷载类型、饱和度、摩擦因数都是影响钢轨体内等效应力分布的重要因素。

2）接触荷载类型直接影响接触斑的几何形状。接触斑内黏滑分布和纵向应力整体分布主要由饱和度控制，接触斑形状主要影响接触斑内的应力水平。

3）摩擦因数越大，蠕滑饱和时最大von Mises 等效应力越大，且越容易发生在表层。

4）接触荷载的类型主要影响钢轨体内的应力水平，对最大von Mises 等效应力发生的位置处于表层还是次表层没有影响。

5）赫兹型接触荷载+全滑动状态的最大von Mises等效应力都大于非赫兹型接触荷载+部分滑动状态，且更易发生在表层。相同加载次数下赫兹型接触荷载+全滑动状态下钢轨会产生更大的塑性变形。因此，以赫兹型接触荷载+全滑动状态为前提的简化轮轨接触疲劳预测模型（如安定图）在进行轮轨接触疲劳分析时，得到的疲劳预测结果偏于保守。