基于最优遍历的巡回采茶问题研究

陈明新　刘嘉旺　戴厚平

摘  要：针对茶农采茶路线最优化的实际问题，本文首先应用奇偶作业点法将抽象出来的茶田区域图（非欧拉图）转化成欧拉图，再以Fleury算法为基础来寻找该欧拉图的最优巡回路线。最后以湖南省湘西自治州保靖县的一片茶田区域为例，对该方法的可行性和有效性進行了说明。通过对比分析，表明利用Fleury算法制定出的采茶路线，可以节约时间及人力，提高茶农采茶的效率，为茶农采茶提供了一些参考和依据。

关键词：采茶路线最优化;奇偶点作业法;Fleury算法

中图分类号：O212                  文献标识码：A文章编号：2096-4706（2021）20-0091-04

Research on Itinerant Tea Picking Problem Based on Optimal Traversal

CHEN Mingxin， LIU Jiawang， DAI Houping

（School of Mathematics and Statistics， Jishou University， Jishou  416000， China）

Abstract： Aiming at the actual problem of optimizing the tea picking route of tea farmers， this paper first applies the odd-even operation point method to convert the abstracted tea field area map （non-Euler diagram） into an Euler diagram. Then， based on the Fleury algorithm， the optimal itinerant route of the Euler graph is found. Finally， a tea field area in Baojing County， Xiangxi Autonomous Prefecture， Hunan Province is taken as an example to illustrate the feasibility and effectiveness of this method. Through comparative analysis， it is shown that the tea picking route developed by the Fleury algorithm can save time and manpower， improve the efficiency of tea picking of tea farmers， and provide some reference and basis for tea farmers to pick tea.

Keywords： optimum tea picking route; odd-even point operation method; Fleury algorithm

0  引  言

自2020年以来黄金茶的生产总量及生产总值都在稳固上升，产业项目建设力度也在不断加大，基地的规模也在不断扩展。政府通过强扶优茶叶新型经营主体，建立贫困户与经营主体的利益联结，充分发挥企业、合作社的示范带动作用，助推产业脱贫攻坚和实现产业持续健康发展.同时为了着力打造优势明显、布局合理、配套完备、品质优异的黄金茶的特色产业集群，各地的人们也都一直在做出不懈的努力。但2020年爆发的新冠疫情导致交通运输严重受阻，消费者活动受限，致使消费行为的发生困难，直接导致黄金茶价格降低，严重滞销。因此，设计有效的采茶路线，可以降低茶农在采茶方面的成本，从而提高茶农的经济收入。茶农采茶问题实质上就是路径规划的问题，目前国内很多学者在路径规划方面做了研究，彭永昆等[1]提出了一种基于回溯的双向完全遍历路径规划算法，实现了工作环境的全覆盖;应沈静[2]等介绍了二叉树的四种遍历方法，实现了四种条件下求解二叉树的程序;陈镜宇[3]研究了智能割草机器人路径规划问题;熊亿民[4]提出了基于改进蚁群算法的全向移动机器人全遍历路径规划方法。这些研究成果开展了最优边遍历的理论探索和实证研究，提供了较好的有益参考。

但是对于茶农采茶路线规划的实际问题，目前鲜有相关参考文献。本文将结合实际的茶农采茶问题，通过实地采集茶田相关数据，利用Fleury算法对茶农的采茶路线进行合理规划，提高茶农采茶的效率，节约人力、物力。

1  采茶问题

采茶一直都是茶农的一项关键工作，采茶过程进行的好与否与茶农经济收入高低有着直接的关系。在采茶期，如果茶农对成熟茶田的采茶路径进行有效规划，可以使得采茶的经济成本明显降低。采茶的目标路径一般为全部成熟或者大部分都成熟了的茶田。在实际的采茶过程中，茶农需将每条目标茶田路径至少走过一遍。茶农从采茶的起点出发，按照预先制定好的采茶路线进行采茶工作，完成所有目标茶田路径的采茶任务后返回起点。在茶农的采茶工作中，采茶路径的设计是关键一环，好的采茶路径可以提高茶农的采茶效率，使得采茶成本最小化，提高茶农的经济收入。当前，茶农主要是依据个人的经验来制定采茶路径，以这样的方式设计出的采茶路线往往不是最优的。茶农采茶问题的关键是优化采茶路线，设计出最短的采茶路线，从而提高茶农的采茶效率。本文基于单茶农和单出发点研究茶农采茶路线优化问题。茶农采茶路线设计的问题类似于图论中的邮递员问题;邮递员以邮局为起点进行邮件分送工作，区域内所有道路都有邮件需要分送，要求沿着道路完成邮件的分送，最后回到邮局，并且保证这个过程中走过的路径总长度最短。通过分析，可以发现茶农采茶路线优化问题与邮递员问题的相似之处。

茶农采茶路线优化问题的模型为：茶农从起点出发去遍历所有目标茶田，最后返回起点。他必须经过每条目标茶田至少一次，要求为茶农设计一条采茶路线，使得整个采茶过程中的路程最短。本文中茶农的起点与邮递员问题中邮递员的起点相似，位于目标茶田道路上。茶农采茶路线优化问题可以抽象为图论的问题，该问题的实际图论模型为：把茶农所遍历的茶田区域网看作是一个带权的连通图G（V，E），E表示茶农遍历区域内的所有茶田，V表示该区域内茶田的交叉点和采茶起点，目标茶田用P表示且有P?E，非目标茶田用P＼E表示，边上的权值代表对应茶田道路的长度，茶农最优采茶路线为求图G的一个包含P中所有边（至少一次）且经过起点的回路，并使得这条回路的所有权值之和最小。

2  算法设计

2.1  奇偶作业法

首先介绍奇偶点作业法[6]以及使用奇偶作业点法使得非欧拉图变成欧拉图的具体步骤。

奇偶作业法实行的依据为：

设C是一条能经过带权连通图G的任意一条边至少一次的回路。C是该带权连通图G的最优回路的充分必要条件是C对应的欧拉图G^*能够满足以下条件：

（1）带权连通图G的每条边在欧拉图G^*中能够重复出现的次数不超过1。

（2）带权连通图G的每个包含重复出现边的圈在欧拉图G^*中的重复出现边的权重之和不超过这个圈的权重之和的一半。

奇偶点作业法实施的具体步骤：第一步：通过任意一个方案找出图中所有奇数点（所连接的边的数量为奇数条），以加边的方式将奇数点进行配对，直至新图中不再出现奇数点为止;第二步：按照路径规划[7]的方法反复计算，直到图中重复的边总长度变短。第三步：按照上述的条件（2）重复执行第二步。

2.2  Fleury算法

当茶田图形可以抽象为欧拉回路时，应用Fleury算法对该茶田图形进行路径搜索，可得到欧拉回路。Fleury算法的基本步骤为：

Step1：任取v₀属于V（G），令P₀=v₀。

Step2：设P_i=v₀e₁v₁e₂…eivi如果EG-{e₁，e₂，…，e_i}中沒有与v_i关联的边，则计算停止，否则从EG-{e₁，e₂，…，e_i}中任取一条边e_i+1。

（i）e_i+1与v_i相关联;

（ii）除非没有别的边可以选择，否则e_i+1不应该是G_i=G-{e₁，e₂，…，e_i}的割边。

Step3：设e_i+1=（v_i，v_i+1），把e_i+1，v_i+1加入P_i。

令i=i+1，返回Step3。

茶农采茶问题路径优化问题的主要逻辑与Fleury算法步骤相对应[8]，首先，判断该图是否为欧拉图，如果不是，则通过奇偶点作业法将其化成欧拉图;其次，确定欧拉回路的采茶起点和起始茶田道路：再次，寻找接下来需要经过的茶田道路和茶田交叉点，直到完成采茶任务;最后，得出采茶路径以及对应的权重，完成茶农采茶路径的优化;

在选择目标茶田道路时，要判断这条茶田道路的终点是否符合Fleury原理的判定，若符合则可以更新采茶路径，以便于进行下一次的采茶过程，若找不到下一个茶田交叉点，则返回之前的步骤重新搜索可以实现的茶田道路。

在选择下一个茶田交叉点时，要进行多次判断：

3  数值算例

3.1  茶田平面图形

本文根据图论理论，将整个茶田区域抽象成一个无向图，并将每个茶田看作一条边，通过Fleury算法搜索出走完整个茶田区域并回到原点的最短路径。在得出最后结果之前，本文对所计算的结果进行了检验，以确保模型的合理性以及算法的可行性。

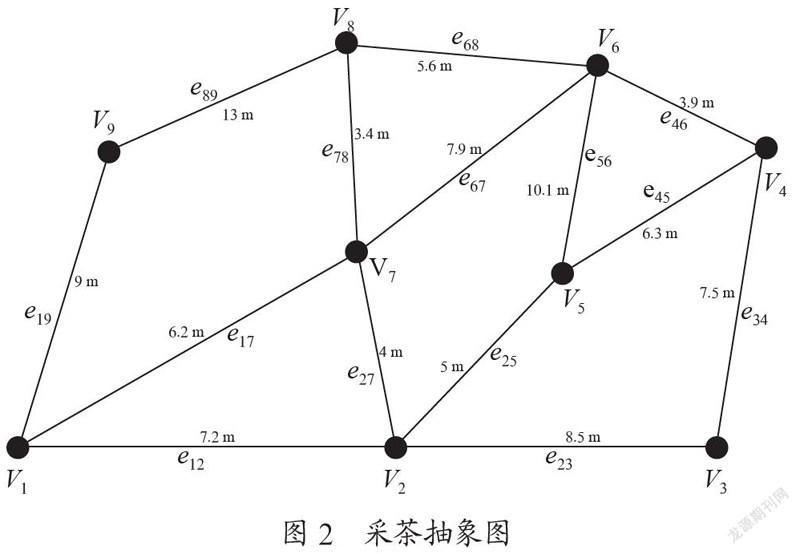
根据图论理论，设茶田区域内各个茶田的交叉点为图G中的顶点，记为V（G）各茶田为图G的边，记为E（G）。本文通过走进茶田进行实地测量，得出了各茶田之间边的权重，具体如下图所示。

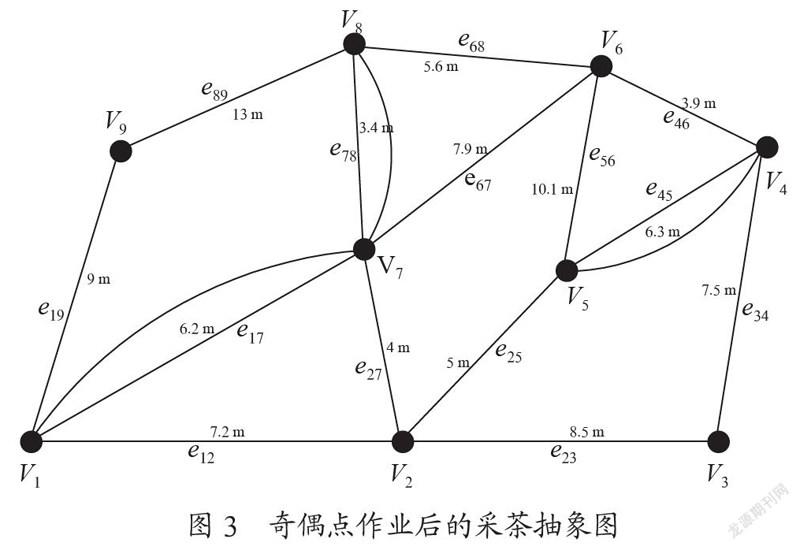
按照奇偶作业法的假设条件，第一步先是判断图G是否是欧拉图。通过条件，我们可以看出在图2中，顶点v₁、v₄、v₅、v₇、v₈是奇数点，所以图2非欧拉图。将非欧拉图转化成欧拉图就需要添加重复边。给v₁、v₇的边增加一条重复的边;给v₄、v₅的边增加一条重复边，给v₇、v₈的边增加一条重复边，且使得增加的重复边权值之最小。据上述分析，可通过奇偶点作业法得到图3，此时图3中无奇数顶点，即为欧拉图。

3.2  检验过程

对图3进行检验，计算已添加重复的边的每个圈的权数和与每个圈所含重复的边的权数之和。如表1所示。

根据表1可知，包含重复边的所有圈所含重复的边的权数之和没有超过该圈的权数总和的一半。因此可以判定此方案为最优方案。

3.3  求解流程

根据Fleury的算法的思想，从起点v₁出发，最终回到v₁。其中求解的部分过程流程如图4所示。

在求解过程中，每一个点选择的边都是与该点相关联的边。特别，如果与该点关联的边为桥且唯一的话，那么仍选择这一条边。上述行进路线可由图5来表示。

将图5所示的茶农采茶的行进路线连接起来，最终我们可以得到茶农在茶田采茶的最优化采茶路线为C={v₁e₁₂v₂e₂₃v₃e₃₄v₄e₄₅v₅e₂₅v₂e₂₇v₇e₆₇v₆e₄₆v₄e₄₅v₅e₅₆v₆e₆₈v₈e₇₈v₇e₁₇v₁e₁₉v₉e₈₉v₈e₇₈v₈e₇₈v₇e₁₇v₁}，由此可以得出边e₁₇、e₄₅、e₇₈各进行了两次，该回路重复走过15.9米。

3.4  对比分析

通过Fleury算法，得出了新的茶农采茶路线。为了评估该采茶路线的合理性和可行性，我们进行了两次采茶工作。第一次按照茶农根据实际经验制定好的采茶路线进行采茶工作，第二次按照新的采茶路线进行采茶工作。最后对比两次采茶工作中茶农的行走距离与所需时间，对比结果如表2所示。

通过分析表2可知，按照Fleury算法制定的采茶路线进行采茶工作，可减少73.5米的行走距离，节约采茶时间16.5分钟。按照一人采茶，一天十次采茶来计算，可节约时间165分钟。因此，依据Fleury算法制定的采茶路线能够节约时间，提高茶农采茶的效率。

4  结  论

本文首先对黄金茶产业现状进行了分析，概括了在疫情条件下茶农在采茶过程中所面临的问题，再介绍了奇偶作业法以及Fleury算法。最后以湖南省湘西土家族苗族自治州保靖縣某一茶田区域为例，对茶农采茶路线进行了研究，验证了Fleury算法在茶农采茶路线问题中的应用，节约效果明显。本文通过运筹学等数学学科知识，寻找茶农采茶最佳遍历路线，希望在茶农采茶实现高质量的同时，能够对提高农民的采茶效率提供一些帮助。

参考文献：

[1] 彭永昆，徐胜，陈元电，等.基于回溯的室内机器人完全遍历路径规划 [J].工业控制计算机，2021，34（6）：33-36.

[2] 应沈静，袁仁斌，陶骏，等.基于遍历求二叉树的程序设计与探讨 [J].科技风，2021（14）：83-87.

[3] 陈镜宇，郭志军，尹亚昆.基于混合算法的智能割草机全遍历路径规划及其系统设计 [J].计算机科学，2021，48（S1）：633-637.

[4] 熊亿民.基于改进蚁群算法的全向移动机器人全遍历路径规划 [J].计算机系统应用，2021，30（6）：209-214.

[5] 李玲玉.基于开源GIS和乡村邮递员问题的交警巡逻路线优化研究与应用开发 [D].上海：华东师范大学，2020.

[6] 管梅谷.奇偶点图上作业法 [J].数学学报，1960（3）：263-266.

[7] 彭光超.基于邮递员问题的深圳供电局变电站巡视路线研究 [D].天津：天津大学，2016.

[8] 侯茂盛，孙明利，杨帆，等.基于改进Fleury算法的激光扫描投影路径规划方法 [J].应用光学，2019，40（3）：493-499.

作者简介：陈明新（2002—），男，侗族，湖南怀化人，本科在读，研究方向：数学与应用数学;

通讯作者：戴厚平（1979—），男，汉族，湖南隆回人，副教授，博士，主要研究方向：微分方程数值解和数学建模。