基于理想点-可拓云模型的隧道围岩稳定性评价
2021-05-08何乐平罗舒月胡启军蔡其杰李浴辉
何乐平,罗舒月,胡启军,蔡其杰,李浴辉
(1.西南石油大学土木工程与测绘学院,四川 成都 610500;2.西南交通大学交通运输与物流学院,四川 成都 610031)
0 引言
随着国家现代化发展的不断加快以及交通基础设施建设的不断推进,人们越发重视地下空间的利用。隧道工程作为地下空间建设的重点工程,尤其受到关注。在隧道工程中,隧道失稳围岩是一系列灾害事故发生的危险源,且隧道围岩的稳定性关系到后续工程设计的合理与否以及施工的安全与否,是隧道工程建设的基础。所以我们有必要提前预警,对隧道围岩进行稳定性评价,预防灾害事故的发生。
对隧道围岩稳定性的研究经历了多个过程,包括定性评估向定量评估的发展以及定性和定量相结合、单指标评估向多指标综合评估的过渡等。专家学者已经研究发现近百种关于隧道围岩稳定性的评价方法[1]。目前,在隧道围岩稳定性评价研究中应用最多是智能多指标评价方法。因为隧道围岩的稳定性受到多种风险因素的共同影响和作用,智能多指标评价方法能够克服早期单一指标评价方法的不足,考虑多种风险因素的综合作用。隧道围岩的稳定性是一个比较复杂的非线性问题,传统的多指标评价方法一般选取几个评价指标,以统一的线性公式或者固定模式进行计算,不符合实际工程特点。所以有必要选择智能多指标评价方法对其进行评判。智能多指标评价方法包括:模糊综合评价法[2]、人工神经网络法[3]、灰色聚类评价法[4]、支持向量机法[5]、集对分析方法[6]等。这些方法都有其各自的特点和优势,为围岩的稳定性评价作出了贡献,但也存在部分问题,比如:人工神经网络法不用人为确定评价指标的权重,但学习样本的数量对其应用有一定限制。支持向量机可以提高机器学习中对于新数据的适应性,但知识获取的瓶颈问题会阻碍其运用[7]。集对分析方法难以确定评估中的差异度系数,不利于工程应用[8]。所以需要我们做进一步的研究,以期为隧道围岩稳定性问题探索更多的可能性。
近年来,许多专家、学者也针对围岩稳定性问题进行了大量深入的研究。周麟[9]将可拓学应用于隧道围岩的稳定性评价中,建立了隧道围岩稳定性评价的物元模型,对围岩稳定性进行了评判。梁桂兰等[10]将熵权法与可拓理论结合,应用于岩体质量评价中。陈丹等[11]建立了基于AHP——可拓学理论的隧道围岩稳定性预测模型,并从多层次多指标的角度出发,对隧道围岩进行等级划分。但其中也存有不足:(1)可拓学中,事物特征对应值通常被视为一个确定的数值,这样就无法充分考虑到隧道围岩稳定性评价研究过程中所存在的模糊性和随机性问题,比如:参数计算过程中的随机性、围岩等级划分存在的模糊性和随机性等。(2)评价指标的权重计算大多采用单一赋权法,而单一赋权法所存在的弊端:主观赋权法过于依赖人的主观经验,主观随意性较强的问题以及客观赋权法完全依赖客观数据,可能会存在较大误差的问题都会影响最终结果的正确性。因此本文考虑利用云模型的优势对可拓理论进行改进,并结合理想点组合赋权法对隧道围岩稳定性进行研究。
1 可拓云理论
1.1 可拓学理论
可拓学[12]是为解决客观世界中所存在的矛盾问题而创立。可拓学应用的范围较广,利用它可以实现不相容的评价指标到融合问题的转化。可拓学中用物元模型R=(N,C,V)作为描述事物的基本元。通常物元模型如式(1)所示:
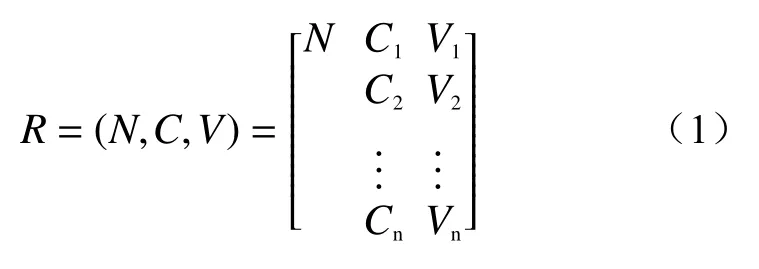
式中:R——事物的基本元;
N——事物名称;
C——事物特征;
V——事物关于特征的量值。
1.2 云模型
云模型[13-14]是由中国科学院院士李德毅在1995年基于模糊、随机理论所提出的。云模型的实质是一种不确定转化模型,通过云模型的基本工具云发生器可以实现事物定量与定性之间的互相转化。云模型能够解决事物中存在的模糊性和随机性等不确定性问题。期望Ex、熵En、超熵He三个数字特征,共同反映其基本特性。期望Ex是隶属云的中心值,也是最能代表等级概念的点值。熵En是对定性概念不确定性大小的度量。超熵He是对熵的不确定性度量,反映熵的离散程度,可通过下式计算:


式中:Xmax——代表评价指标关于评价等级的上限边界;
Xmin——代表评价指标关于评价等级的下限边界,对于存在单边界限的评价指标,可以根据其最小下限或最大上限确定缺省边界参数。
k——常数,可根据经验或实际情况自行确定,本文中k取值0.01。
1.3 可拓云模型
可拓云模型就是将可拓理论与云模型相结合,综合利用二者各自的优势对事物进行评价研究。在实际工程或者客观事物中,不确定性的存在会影响风险评价的结果。传统的物元可拓模型中,V值通常被看作表示指标测量值或界限值的确定数值,忽略了客观事物具有的模糊性和随机性。所以利用云模型具有处理事物双重不确定性的优势对其进行改进,将期望Ex、熵En和超熵He代替V值表示关于事物特征的量值,由此得到可拓云模型如式(5)所示:
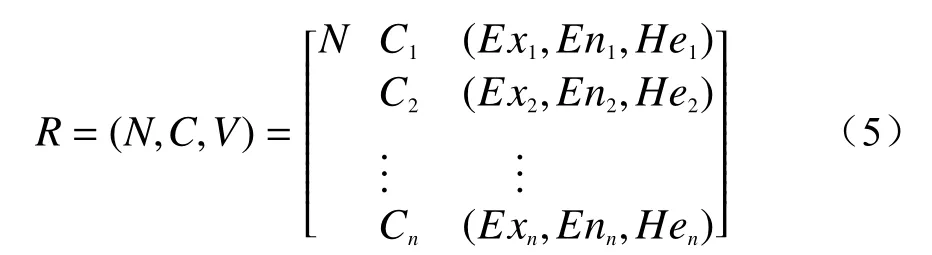
式中:R-评价等级;
Cn-第n个评价指标;
(Exn,Enn,Hen)-表示指标关于该等级的云描述。
本文选择基于正态云模型,通过正向云发生器实现定量与定性之间的转化生成云模型图,求取云关联度。将样本的评价指标数值x看作一个云滴,运用MATLAB 2019a 编程软件,产生一个以En为期望值、He为标准差的随机数En′,且此随机数服从正态分布。再由公式计算出x与可拓云模型之间的关联度u[15]:

通过可拓云模型获得的云关联度具有随机性,相较于以往的物元可拓模型用固定的线性关联函数求得的关联度,将确定的数值由一个不确定的随机数代替,更满足各类实际工程的特性。
2 理想点组合赋权法
2.1 改进的层次分析法计算主观权重
层次分析法常用于计算指标主观权重,它是通过行业专家用1~9 之间的数字来表示各评价指标间的重要性关系,构造比较判断矩阵,再计算评价指标的权重。但有时存在部分重要度相差不大的指标求出权重相差过大的问题。所以,为了减小误差,提升精度,本文对层次分析法进行了改进,将原有用于标度指标重要性的数字差距缩小,选择用1、1.5、2、2.5、···、9 来标度指标间的重要度,再根据基本计算步骤[16]对评价指标的主观权重进行计算。
2.2 熵权法计算客观权重
本文选用熵权法计算评价指标的客观权重。熵权法是一种用于求取客观权重的赋权方法,它是利用收集或测量得到关于事物的客观数据本身来求取评价指标的权重,具体计算方法参见文献[17]。
2.3 理想点法计算组合权重
理想点组合赋权法的基本思想[18]是使向量目标函数与所考虑问题的理想点偏差最小,即使求得的主观权重和客观权重与理想点的差异最小,然后通过构造数学规划模型求解各评价指标的组合权重。
假设求出的评价指标主观权重为p=(p1,p2,···,pn),客观权重为q=(q1,q2,···,qn),待求组合权重为w=(w1,w2,···,wn),定义各个指标属性的理想值为ri*(i=1,2,···,n),进而定义理想方案A*=(y1,y2,···,yn)=(w1r1*,w2r2*,···,wnrn*)。计算方案g到理想点的距离为:

dg越小,则方案g与理想方案越接近。
为计算简便, 对向量进行单位化, 令
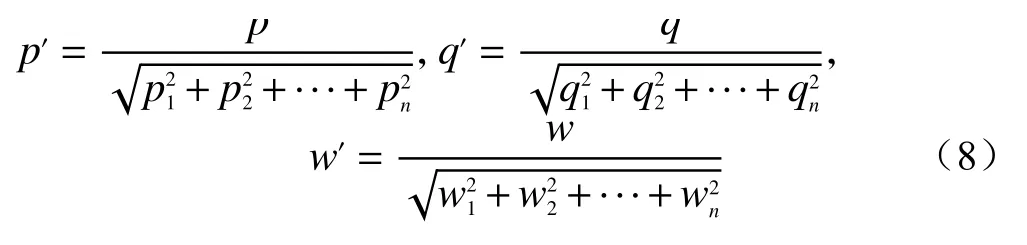
对应于p、q、w各方案Ag到理想点的距离的平方和为:
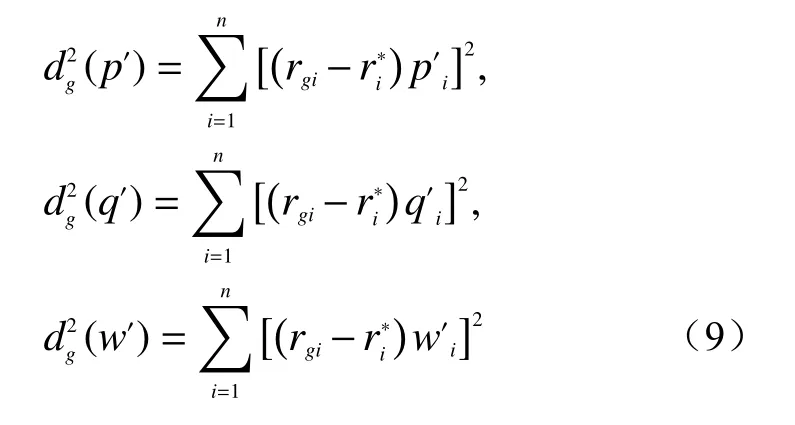
为了减少使用单一的主、客观赋权法所产生的误差,且兼顾二者,所以选择组合赋权。建立非线性规划模型如下所示:
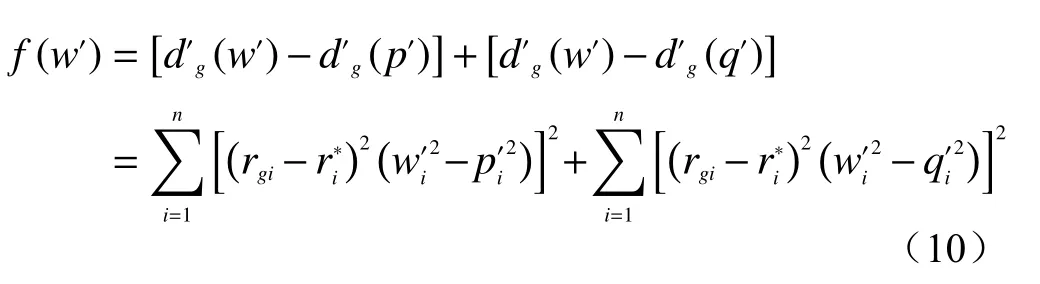
通过构造拉格朗日函数解得:
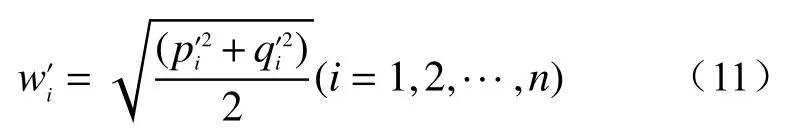
组合权重为:
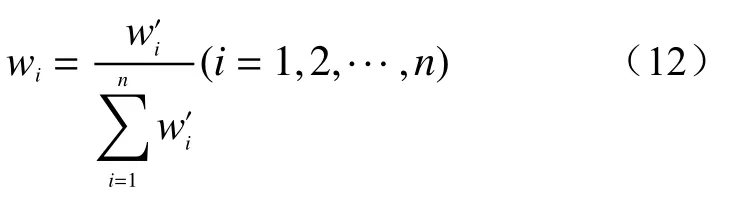
式中:p——评价指标主观权重;
q——评价指标客观权重;
w——评价指标组合权重;
n——评价指标总数;
i——第i个评价指标;
ri*——指标属性的理想值;
A*——理想方案;
y——指标加权值;
g——任意方案;
d——任意方案与理想方案的距离;
f——非线性规划模型。
3 基于理想点——可拓云模型的隧道围岩稳定性评价研究方法
3.1 隧道围岩稳定性评价研究流程
(1)选取隧道围岩稳定性评价指标,并根据相关规范以及已有文献对隧道围岩等级进行划分。
影响隧道围岩等级的风险因素种类较多,且这些因素之间会互相影响,共同作用。评价指标的选取会关系到隧道围岩评价指标体系的合理构建以及最终围岩等级划分的正确性,所以本文通过文献调研、数据统计的方式,选取风险评价指标建立隧道围岩稳定性评价指标体系。对从中国知网查阅收集的50 篇围岩相关文献进行统计分析,总共出现83 种共310 个有关围岩的评价指标。利用柱状图对出现频数较高的部分评价指标进行了统计(图1)。其余指标均出现1~3 次不等。
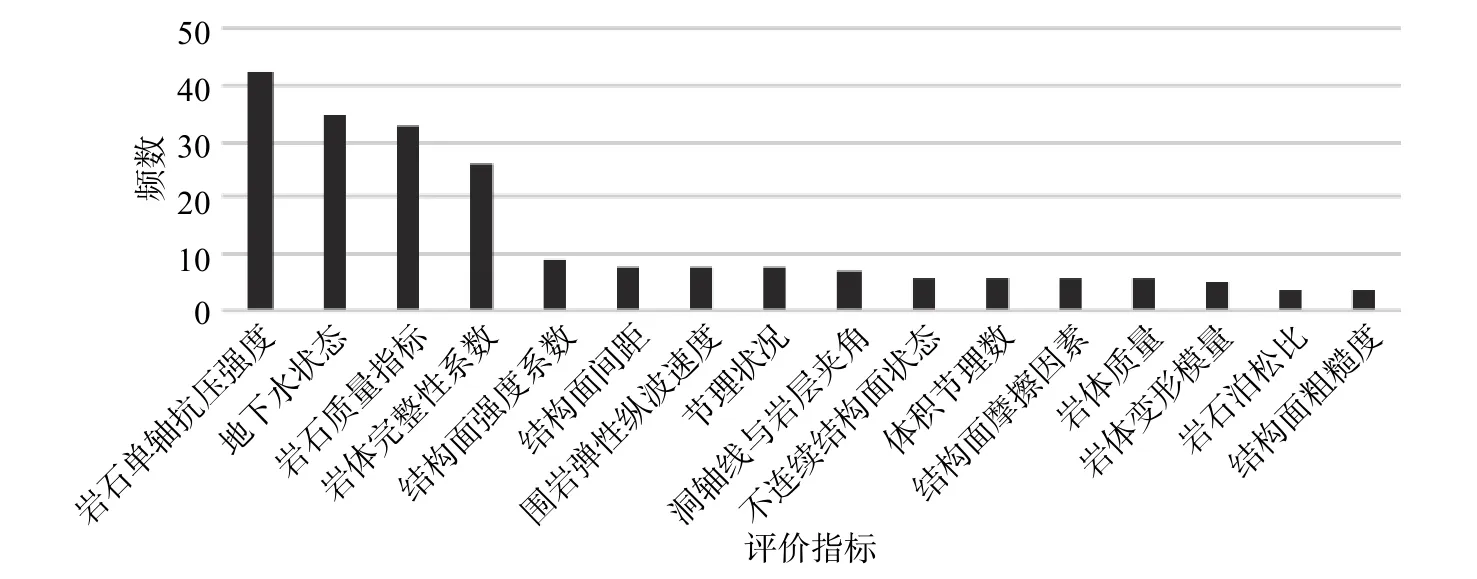
图1 评价指标频数统计Fig.1 Evaluation index frequency statistics
由图1可知,出现的指标种类众多,若将所有指标都作为隧道围岩稳定性的评价指标是暂无法实现的,需要根据隧道围岩的岩性特点、岩体结构以及对隧道围岩等级的影响程度选择。根据《工程岩体分级标准》[19]可知,岩石坚硬程度和岩体完整程度共同决定岩体基本质量,首先从这两方面选取具有代表性且易于测得的评价指标。岩石单轴抗压强度是出现频率最高的一个评价指标,它是从定量的角度反映岩石的坚硬程度,应用最广泛,具有较强的代表性。岩体完整性系数,是一个较为重要的指标,从定量的角度反映岩体完整程度。岩石质量指标,在文献中出现的频率较高,它是从侧面体现岩体的完整性,可以与岩体完整性系数结合,共同反映岩体的完整程度。在地下空间工程中,总是受到地下水环境影响,地下水会软化岩土,使其强度降低,很大程度上不利于隧道围岩稳定性,所以考虑地下水状态作为评价隧道围岩稳定性的指标。再从整体性、相关性和反映岩体本质特点出发,选择出现频率较高的围岩弹性纵波速度和体积节理数二者作为评价指标。
通过对隧道围岩的特点进行分析以及查阅相关标准[19],将其划分为5 个等级,分别是:Ⅰ类(稳定)、Ⅱ类(基本稳定)、Ⅲ类(稳定性差)、Ⅳ类(不稳定)、Ⅴ类(极不稳定)。再根据文献[20 - 22],将选取的6 个评价指标的连续属性值离散为5 个等级,分别对应划分的Ⅰ-Ⅴ评价等级(表1)。

表1 隧道围岩稳定性评价指标分类标准Table 1 Classification criteria of tunnel surrounding rock stability evaluation index
(2)确定待评物元
(3)利用改进AHP 和熵权法分别计算评价指标的主、客观权重,再由理想点赋权法求取组合权重。
(4)通过评价指标的云关联度和权重得到对应各评价等级的综合确定度,根据式(13)计算。
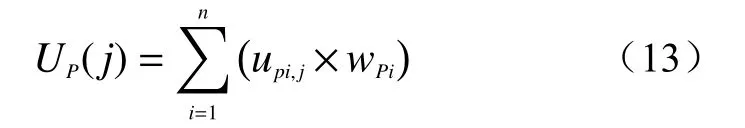
式中:P——待评价样本;
j——第j个评价等级;
Up(j)——待评价样本P关于评价等级j的综合确定度;
upi,j——相应的关联度;
wpi——相应的组合权重。
(5)通过综合确定度最大的原则来确定待评价样本所属的评价等级。设待评价样本所属等级为R,则:
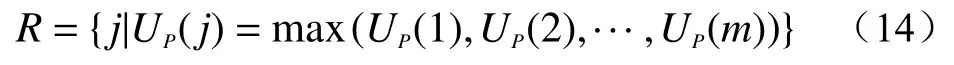
式中:R——待评价样本等级;
m——评价等级总数。
流程图如图2所示:
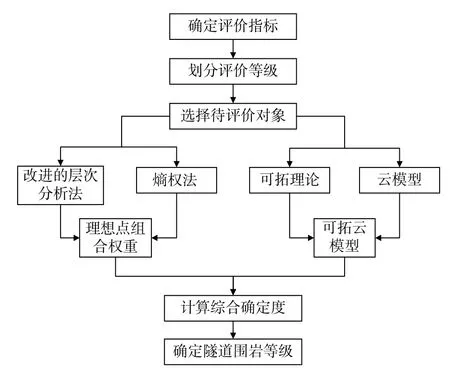
图2 隧道围岩稳定性评价流程图Fig.2 Flow chart of tunnel surrounding rock stability evaluation
3.2 隧道围岩稳定性评价研究公式整合
假设某待评价样本P关于某个风险评价指标i的数据值为a,则该指标i关于某个等级j的关联度为
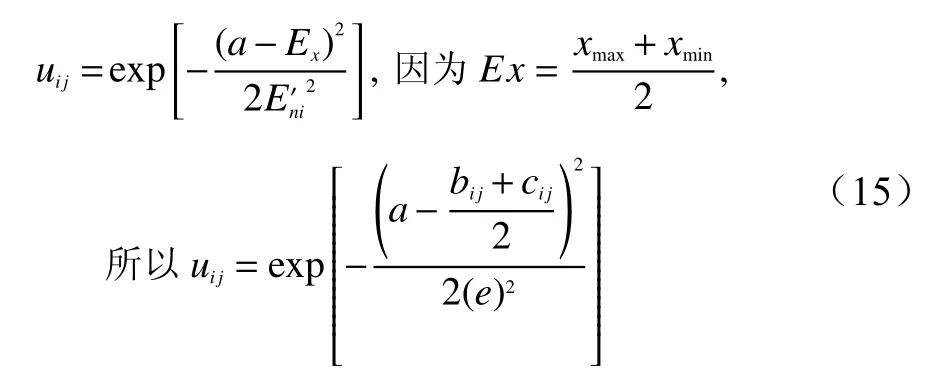
假设已经求得的主观权重为p=(p1,p2,···,pn),客观权重为q=(q1,q2,···,qn),待求组合权重为w=(w1,w2,···,wn),则
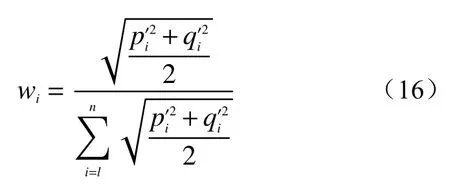

式中:a——待评价样本关于评价指标的数值;
b——评价指标关于某个评价等级的上限数值;
c——评价指标关于某个评价等级的下限数值;
e——En′。
根据综合确定度最大的原则,待评价样本等级为R={j|UP(j)=max(UP(1),UP(2),···,UP(m))}。
4 工程实例
本文选用文献[22]中的广大铁路祥和隧道的5 个代表性洞段为例(表2)。采用理想点——可拓云模型的方法对实例中隧道围岩稳定性进行评价研究,以验证此方法的可行性和有效性。

表2 样本指标实测值Table 2 Sample index measured value
4.1 隧道围岩稳定性评价标准云模型
根据式(2)(3)以及表2中的数据,可求得各评价指标关于各个评价等级云模型的三个数字特征,得到关于隧道围岩等级的标准云模型(表3)。

表3 隧道围岩等级标准云模型Table 3 Standard cloud model of tunnel surrounding rock grade
利用MATLAB 2019a 软件编写程序并输入表3中数据,通过正向云生成器就可得到图3所示的云图。图3(a)——图3(f)是分别对应于6 个评价指标的云模型图。在云模型图中,横、纵坐标分别表示评价指标的取值和与之对应的云关联度。图3(a)(b)(c)(e)是从左到右依次表示等级Ⅴ~Ⅰ的云图,图3(d)(f)是从左到右依次表示等级Ⅰ~Ⅴ的云图。
4.2 隧道围岩稳定性评价指标权重计算
改进层次分析法计算出各个评价指标的主观权重为:(0.359,0.082,0.160,0.225,0.115,0.059),用熵权法计算的评价指标的客观权重为:(0.159,0.179,0.150,0.171,0.169,0.172),通过理想点组合赋权法求得的组合权重为:(0.252,0.140,0.148,0.187,0.142,0.131)。
4.3 综合确定度计算及围岩等级确定
现在以样本4 为例,先根据式(6)计算出样本4 的6 个评价指标的云关联度,且云关联度分别对应于划分的5 个评价等级。再通过式(13)计算出样本关于各评价等级的综合确定度:U4(Ⅰ)=0.000 000,U4(Ⅱ)=0.000 000,U4(Ⅲ) = 0.000 038,U4(Ⅳ) = 0.597 523,U4(Ⅴ)=0.000 004。因为U4(Ⅰ)=U4(Ⅱ)<U4(Ⅴ)<U4(Ⅲ)<U4(Ⅳ),根据综合确定度最大的原则,所以样本4 属于等级Ⅳ。同样,可用此方法获得其余待评价样本的围岩等级。如表4所示,样本1 属于等级Ⅳ,样本2 属于等级Ⅲ,样本3 属于等级Ⅴ,样本5 属于等级Ⅴ。为了验证理想点——可拓云模型在隧道围岩稳定性评价研究中结果的正确性,将获得的结果与熵权——云模型、可拓理论等方法所得结果进行对比分析(表4)。
4.4 对比结果及分析
由以上对评价指标的权重计算结果可知,影响隧道围岩稳定性的指标按重要性和影响程度排序是:Rc、W、RQD、Kv、Vmp、Jv。所以,在对隧道围岩稳定性进行评判时,要着重考虑前两个因素。将所得评价结果与通过熵权-云模型、可拓理论等方法所得结果进行对比分析,样本1、样本2、样本4、样本5 评价结果一致,而对于样本3,可拓理论所得结果为等级Ⅳ,本文评价结果为等级Ⅴ与其余方法结果相同,说明将理想点-可拓云模型应用于隧道围岩稳定性评价是可行的。且本文获得结果属于安全,避免了评价结果偏风险,有利于保证日后隧道工程建设的安全性。实例中5 个样本稳定性都处于等级Ⅲ及以下,说明该隧道围岩稳定性较差,有必要采取相关技术措施对该隧道围岩进行加固、支护等处理,降低风险,提高隧道围岩的安全性和稳定性,预防地质灾害和工程事故的发生[23-25]。
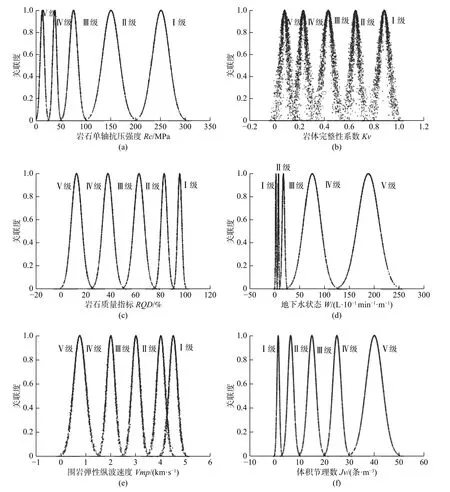
图3 评价指标云图Fig.3 Evaluation indicator cloud diagram

表4 样本评价结果及对比Table 4 Sample evaluation results and comparison
5 结论
通过文献调研、数据统计的方式,选取6 个相关风险因素建立评价指标体系,再针对隧道围岩稳定性评价中存在的不确定性问题和权重求取合理性问题,建立理想点-可拓云模型对其进行稳定性评价,得到如下结论:
(1)将云模型融入可拓理论中,能考虑并解决隧道围岩稳定性评价中存在的模糊性和随机性问题,综合利用二者的优势进行评价,可直接用原始数据进行计算求解,不需对数据进行无量纲化或者规范化等进一步处理,降低了数据计算错误、丢失的可能性,提高了结果的正确性,最终不仅能得到隧道围岩所属等级,还能获得围岩属于各个等级的确定度,有利于工程后期的设计、施工工作。
(2)选用理想点组合赋权法,克服了单一方法计算指标权重过于主观或客观的问题,同时兼顾主观权重即专家经验、专业知识和客观数据在权重求取中的作用,提高了权重及最终评估结果的准确性。
(3)将理想点-可拓云模型运用于工程实例进行检验,所得评价结果与熵权-云模型、可拓理论所得结果基本一致,表明基于理想点-可拓云模型的方法在隧道围岩稳定性评价中是可行且适用的,具有实际操作性。
(4)由于地质条件和环境不同,隧道围岩具有多种类型。本文所收集的工程实例数量有限,是否对于各种地质类型的隧道围岩都适用于本方法,还需通过收集各类隧道工程数据,建立数据库,进行进一步的分析与验证,以证明本方法的普遍适用性。
