基于增量加载法的泥石流拦挡坝抗冲击力数值模拟——以甘肃舟曲三眼峪沟泥石流拦挡坝为例

刘兴荣，魏新平，陈豫津，王翔宇

（1.甘肃省科学院 地质自然灾害防治研究所，甘肃 兰州 730000；2.甘肃省地质环境监测院，甘肃 兰州 730050；3.中国石油西南管道贵阳输油气分公司，贵州 贵阳 550000）

2010年8月8日凌晨，舟曲县城北侧三眼峪沟和罗家峪沟同时暴发特大山洪泥石流，城区三分之一被淹，共造成1 435 人死亡，330 人失踪，直接经济损失超过10 亿元[1-2]，给舟曲县城居民生命财产造成了巨大损失，也给当地生产生活带来严重困难。灾害引起了党中央、国务院、中央军委及全国人民的高度关注，启动国家二级救灾应急响应，同时批复专项资金进行治理。其中，重力式拦挡坝是舟曲泥石流治理中的最主要工程之一。

周龙茂等[3]认为拦挡坝在泥石流治理中发挥着重要作用，但同时拦挡坝也是最易遭受破坏、失去防灾功能的泥石流防治构筑物，因此，在泥石流设计中，为了拦挡坝不被破坏，往往设计得很保守，王念秦等[4]提出这种设计容易造成两个极端现象：保守，造成资金浪费；冒进，防治工程失败。要做到既能保证拦挡坝安全，又能将投资最小化，就要求对泥石流拦挡坝抗冲击力验算方法提出新要求。传统的泥石流冲击力计算经验公式[5]只能通过大量试算表述结果，不能表述过程。而将三维有限元数值分析方法应用到泥石流拦挡坝稳定性验算中[6-7]，能将过程和结果同时呈现，即通过分步加载的方法，逐步呈现拦挡坝的位移情况和抗冲击力过程中的破损情况。

关于拦挡坝的数值模拟研究还比较少，本文将考虑损伤的混凝土本构模型与有限元计算方法相结合，对舟曲泥石流混凝土拦挡结构进行力学分析，最终确定了拦挡坝的抗冲击力合理区间，以期为泥石流治理工程的设计提供借鉴。

1 模型建立及相关参数的设定

杨东旭等[8]、许海亮等[9]、张睿骁等[10]认为冲击力是破坏防治工程构筑物的主要作用力之一，其大小与泥石流流量、流速、容重等有关。泥石流冲击力是泥石流防治工程设计的重要参数，分为流体整体冲击力和个别石块的冲击力两种，在设计中取两种计算结果较高者为设计依据。文章采用《泥石流灾害防治工程设计规范》(DZT 0239——2004)中的经验公式[5]作为数值计算结果的参考和验证。

流体整体冲击力计算公式：

式（1）中：f-冲击力/Pa；

K-系数，取2.5；

γC-泥石流重度/（t·m-3）；

g-重力加速度，取9.8 m·s-2；

vc-断面处泥石流流速（m·s-1）。

个别石块的冲击力计算公式：

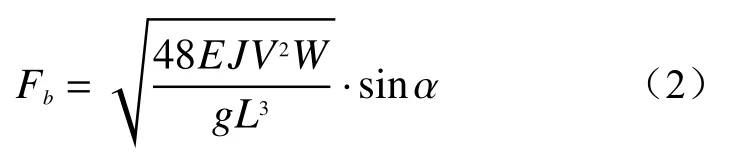
式（2）中：Fb-泥石流大石块冲击力/（t·m-2）；

E-工程构件弹性模量/（t·m-2）；

J-工程构件界面中心轴的惯性矩/m4；

V-石块运动速度（m·s-1）；

W-石块重量/t；

L-构件长度/m；

α-石块运动方向与构件受力面的夹角/（°）。

泥石流具体参数和计算结果见表1，编号和《甘肃省舟曲县三眼峪沟泥石流灾害设计报告》[1]中保持一致。

表1 泥石流冲击力计算参数及结果Table 1 Debris flow impact calculation parameters and results

计算区域按地质资料分高程、分区域模拟。模型向上游及下游分别延伸至坝体厚度的2 倍，模型高度方向自坝基向下延伸坝体垂直部分的2 倍。以大2 号坝为例进行数值模拟，砼坝体和地基土数值分析具体参数见表2。

表2 混凝土坝和地基碎石土参数Table 2 Concrete dam and gravel soil parameter

分析中将泥石流流体的冲击力P简化为静力加载到坝体侧面，计算坝体的极限抗冲击能力，简化计算力学模型如图1所示。

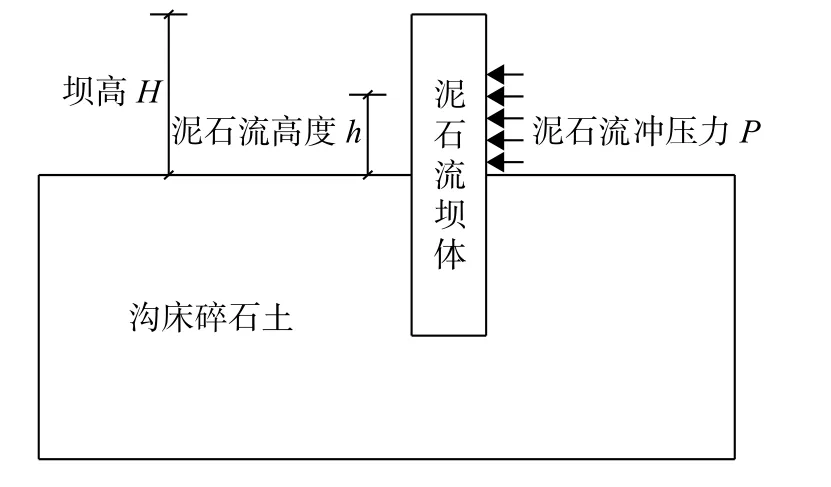
图1 简化力学模型示意图Fig.1 Mechanical model of concrete dam

2 重力式拦挡坝抗冲击力数值分析

数值模拟使用有限元软件ABAQUS 进行计算分析。冯帅等[11]认为数值计算出的泥石流的极限抗冲压力大于经验公式计算出的泥石流整体冲击压力。因此，本文分别按泥石流流体高度h=H/2 坝高（工况1）及h=H（工况2）两种工况进行分析，将数值计算出的抗冲击力限定在一合理区间。计算中加载每一荷载增量后均计算至收敛，并记录坝体的最大位移。加载至破坏时（计算不收敛，坝体位移不断增大）的压力P与坝体最大位移曲线由倾斜直线变为水平线，坝体所能承受的最大冲击力Pu可由压力P与坝体最大位移曲线水平段的和坐标求出。应力以拉为正，以压为负，应力的单位为Pa，长度单位为m，位移单位为mm，其他单位均采用国际单位制。具体模型边界和网格划分图2所示。

图2 模型边界和网格划分Fig.2 Model boundary and meshing

2.1 工况1 条件下重力式拦挡坝抗冲击力数值分析

大坝按泥石流冲击高度h=H/2 坝高计算，在拦挡坝的一侧施加泥石流冲击力，荷载增量取值100 kPa，每加一次荷载，计算至收敛，并且记录一次坝体的最大位移；一直持续加载至破坏时，即计算不收敛且坝体位移不断增大时停止计算。

周勇等[12]采用结构动力学的方法，建立了泥石流冲击荷载与拦挡坝的动力方程，提出拦挡坝的坝顶处有最大的位移，为本次工程力学计算提供了一种思路。将泥石流冲击力与相应荷载下坝体位移进行统计，形成图3所示冲击力与坝体最大位移关系曲线，会发现坝体水平位移随着拦挡坝冲击力增大呈对数曲线递增，泥石流流体高度h=H/2 工况条件下施加的最大冲击力Pu=3 500 kPa（357.14 t/m2）。

图3 冲击力与坝体最大位移曲线（h=H/2）Fig.3 Pressure and the maximum dam displacement curve（h=H/2）

坝体损毁过程如图4所示，冲击力达到800 kPa（水平位移1 mm）时坝体开始出现初始损伤；冲击力达到1 100 kPa（水平位移1.4 mm）时两侧坝肩和基础局部都出现较明显损伤；冲击力达到1 400 kPa 时（水平位移2 mm），泄水孔和泄水涵洞边缘出现局部损伤；冲击力达到2 700 kPa（水平位移4.8 mm）时，基础出现大面积损伤，沿正面泄水涵洞和泄水孔形成纵向损伤；冲击力达到3 200 kPa（水平位移7.2 mm）时，坝肩、基础及坝体正中损伤贯通，损伤区呈“W”型，坝体已基本失去功能，在工程实际应用中已达到破坏极限；冲击力达到3 500 kPa 时，坝体大面积损伤，超过坝体总面积的2/3，水平位移高达14 mm，整体性降低或消失，这只是一种模拟现象，在工程实际应用中泥石流物质沿坝体破坏处流通，坝体已不存在整体位移现象。

图4 不同泥石流冲击力下拦挡坝的损伤情况（h=H/2）Fig.4 Damage of piles under different impact force of debris flow（h=H/2）

2.2 工况2 条件下重力式拦挡坝极限抗冲压数值分析

大坝按泥石流冲击高度h=H坝高计算，荷载增量取值125 kPa，每加一次荷载，计算至收敛，同时记录一次坝体的最大位移，将泥石流冲击力与相应荷载下坝体位移进行统计，形成图5所示冲击力与坝体最大位移关系曲线，会发现坝体水平位移随着拦挡坝冲击力增大也呈对数曲线递增，泥石流流体高度h=H工况条件下施加的最大冲击力Pu=2 490 kPa（254.08 t/m2）。

图5 冲击力与坝体最大位移曲线（h=H）Fig.5 Pressure and the maximum dam displacement curve（h=H）

坝体损毁过程如图6所示，冲击力达到375 kPa（水平位移1.7 mm）时坝体开始出现初始损伤；冲击力达到500 kPa（水平位移2.3 mm）时两侧坝肩和基础局部都出现较明显损伤；冲击力达到1 250 kPa（水平位移6.6 mm）时，泄水孔和泄水涵洞边缘出现局部损伤；冲击力达到1 500 kPa（水平位移8.4 mm）时，基础出现局部损伤，沿正面泄水涵洞和泄水孔形成纵向损伤，两侧坝肩损伤较严重；冲击力达到2 000 kPa（水平位移14.8 mm）时，严重损伤区呈“W”型，坝肩、基础和坝体中心部位损伤基本贯通，坝体已基本失去功能，在工程实际应用中已达到破坏极限；冲击力达到2 490 kPa 时，坝体大面积损伤，超过坝体总量的2/3，水平位移高达40.4 mm，整体性降低或消失，这也只是一种模拟现象，在工程实际应用中泥石流物质沿坝体破坏处流通，坝体已不存在整体位移。

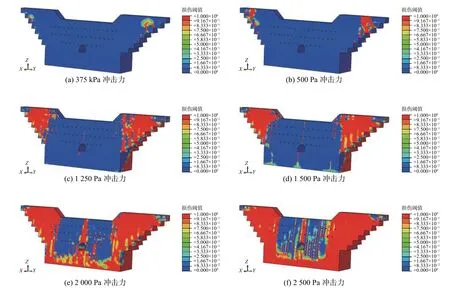
图6 不同泥石流冲击力下拦挡坝的损伤情况（h=H）Fig.6 Damage of piles under different impact force of debris flow（h=H）

3 坝体冲击力安全验算

同样方法计算三眼峪及各支沟泥石流重力式拦挡工程冲击力，得到表3，结合表1可以看出，泥石流经验公式计算的单宽冲击力均小于工况1 数值模拟验算结果，均大于工况2 数值模拟验算结果，与工况1 和2 的平均值接近。2012年建成至今，大部分坝体库容淤积过半，部分甚至已淤满，说明拦挡坝经受住了各种泥石流冲击破坏的考验。

4 讨论

4.1 泥石流冲击高度对坝体影响

将2 种工况进行比较，工况1 的冲击力达到800 kPa时坝体开始出现初始损伤，最大冲击力为3 500 kPa，而工况2 的冲击力达到375 kPa 时桩体开始出现初始损伤，最大冲击力为2 490 kPa。说明冲击高度对坝体的影响较大，随高度增加，达到初损的冲击力荷载几乎成倍数减少，而最大冲击力也减少1 000 kPa。这说明在拦挡坝设计中泄水涵洞和泄水孔的预留很重要，为减少拦挡坝的冲击破坏，应尽量选择低坝，同时在不影响坝体安全和停淤功能的基础上，应多布设泄水涵洞和泄水孔，降低坝前壅水位，最大可能避免或减少高水位过流。

4.2 拦挡坝损伤过程对拦挡坝设计的指导意义

拦挡坝的损伤从两侧坝肩开始，再到拦挡坝中间部位的泄水涵洞及泄水孔边缘，然后到基础，最后坝肩、中间部位和基础形成“W”型的贯通破坏，其破损部位按先后顺序依次为“坝肩——泄水涵洞及泄水孔——基础——“W”型贯通”4 个过程。设计时应重点考虑这几处薄弱环节，要相应的进行专门的加固处理。

4.3 拦挡坝冲击力设计的合理范围

从安全和经济方面考虑，在拦挡坝设计中冲击力的考虑应该取工况1 和工况2 之间值较合理，工况1 存在风险，工况2 偏保守，而工况1 和2 的中间值接近经验公式计算冲击力。从表3中可知，三眼峪设计中的冲击力选择也是工况1 和2 的平均值，从而保障了拦挡坝的安全运行。

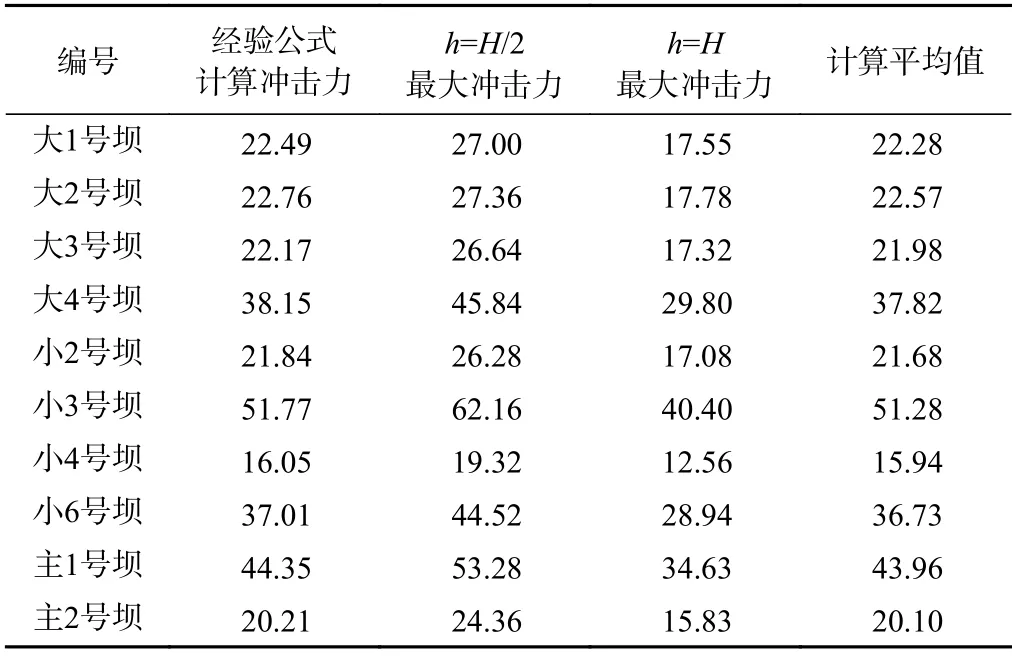
表3 重力坝冲击力数值模拟验算结果对比表（单位：t/m2）Table 3 Comparison of results of numerical simulation of impact of gravity dam (unit: t/m2)

4.4 可作为现有泥石流设计理论的有效补充

由于真实模拟泥石流重力式拦挡坝的室内大型实验难度比较大，野外测定随机性太大，故本文采用数值模拟的方式来分析三眼峪沟拦挡坝的受力情况。结果表明数值模拟对分析问题有一定的指导意义，可以和现有的泥石流设计理论结合，为以后工程设计提供安全对比，但是不能代替物理实验和理论计算。

5 结论

（1）本文通过有限元软件ABAQUS 进行拦挡坝数值模拟计算和分析，比较2 种工况条件发现：随着泥石流冲击高度增加，达到初损的冲击力荷载成倍数减少，而最大冲击力也减少1 000 kPa；拦挡坝的损伤从两侧坝肩开始，再到拦挡坝中间部位的泄水涵洞及泄水孔边缘，形成“W”型的贯通破坏。

（2）通过与经验公式计算冲击力比较，发现拦挡坝设计中冲击力选择工况1 和2 的平均值较合理，可以为工程设计提供安全对比。