一种基于射频指纹的电网无线设备入侵检测算法
2021-05-08陈子骁周小明刘晓凯许方敏
陈子骁,周小明,李 钊,刘晓凯,许方敏
(1.北京邮电大学 信息与通信工程学院,北京 100876;2.国家电网辽宁省电力有限公司,辽宁 沈阳 110004;3.北京物联智通科技有限公司,北京100000)
0 引言
泛在电力物联网的广泛建设,开启了电网企业新一阶段的信息化浪潮。泛在电力物联网是与原有智能电网共生的系统,它可以实时地连接能源生产、传输、消费等各个环节的设备、数据和客户,具有无线设备广泛联接、平台开放共享、计算边云协同、数据分析挖掘、应用可以客制化等特征。随着智能电表等无线终端设备的普及,泛在电力物联网需要管理的无线终端设备日益增多,这对泛在电力物联网提出了大规模无线终端设备管理和数据采集的急迫需求。随之而来的是诸多安全风险,如数据安全管理、终端入侵检测、网络环境安全性等。因此,泛在电力物联网对于轻量级的无线终端入侵检测识别有着非常强烈的需求。
1 射频指纹识别研究现状
近年来,射频指纹识别取得很大的进展,越来越多的学者和研究机构着眼于用射频指纹识别无线设备这个领域。射频指纹的最大优势在于它使用了发射机固有的硬件差异进行识别,却无法用任何其他设备进行复制,因为复制设备会在复制的发射信号上添加自己的特征,因此射频指纹是很难完全复制的。关于射频指纹的研究始于1995年,到目前为止,射频指纹技术有2种类型:基于瞬态和基于稳态。Hall等人[1-2]利用频率和幅度信息从10种不同的瞬态特征创建射频指纹,以识别无线局域网和蓝牙发射机。Afolabi等人[3]使用了一个仿真模型,并通过使用振幅、相位和频率曲线从预处理的瞬态信号中提取了6个特征来形成射频指纹。Ellis等人[4]用基于幅度和相位信息创建的射频指纹识别。近期研究中基于瞬态的射频指纹主要是从瞬时特性(幅度、相位和频率)[5]和时间频率分布[6-7]中提取的。尽管基于瞬态的方法表现出了很好的性能,但仍然存在一些挑战[8]。这主要是因为瞬态信号持续时间太短,对信号采集设备提出了很高的要求。与基于瞬态的射频指纹相比,基于稳态的方法更适合工程实施。基于稳态的射频指纹方法于2008年首次提出,Rehman等人[9]提出了利用通用移动电信系统(UMTS)的前同步码信号频谱识别8个相同的发射机,该方法运行良好,在30 dB信噪比(SNR)时能够达到97%的分类率。继这项研究之后,近年来不断提出有关基于稳态的射频指纹的新方法,例如调制信号[10-11]的独特信号特性、前同步信号[12-13]的功率谱密度和RF-DNA指纹[14-15]等。虽然现在射频指纹识别的研究取得了一定进展,但在泛在电力物联网的应用场景中,射频指纹识别的稳定性和准确率还是表现不佳。射频指纹特征的选择和提取以及射频设备的识别分类仍是一个难题。
本文设计了一种基于射频指纹的电网无线设备入侵检测系统和算法。本文的创新点和工作量如下:
① 基于信号局部双谱积分提取的射频指纹特征的识别分类方案,将这5种分类方案仿真并相互对比,分析5种信号局部双谱积分的优劣势,并通过仿真得出结论,矩形积分双谱(Square Integral Bispectra,SIB)和选择双谱对于射频信号的区分度最优。
② 基于射频信号的双谱特征可以抑制加性高斯白噪声的特点,提出了基于SIB和选择双谱的融合特征。对比使用传统信号特征的支持向量机(Support Vector Machine,SVM)模型和使用基于SIB和选择双谱的融合特征的SVM模型,经过实验论证,本文提出的基于SIB和选择双谱的融合特征的SVM模型在电网无线设备入侵检测中具有更高的准确率。
本文的其余部分安排如下,第2节论述了射频指纹特征产生的原理,详细分析了射频信号的双谱特征和局部积分双谱,并设计了一种新的射频指纹特征——基于SIB和选择双谱的融合特征。第3节分析了SVM分类算法,第4节提供了实验系统的设置和评估,第5节对本文的研究工作进行了总结。
2 双谱特征分析与提取
在电网的生产环境中,无线终端发射的射频信号经过编码与调制后一般是非线性非平稳的非高斯信号,表示为:
x(n)=z(n)+A×exp[j(ω0nT+θ)],n=0,1,…,N,
(1)
式中,z(n)为一段均值为0,方差为σ2的复高斯信号;A为信号幅度;ω0为信号载频;θ为射频信号的初始相位;T为采样间隔。如果用信号的一阶矩或二阶矩去分析这些信号,效果较差。为了提取与射频信号分类相关性更强的特征,使无线终端设备可以更好地被分类识别,本文选择从信号的高阶统计量入手。大量研究表明,信号的高阶统计量中,高阶谱参量在抑制高斯色噪声方面表现卓越,是分析非平稳信号的良好特征。
2.1 高阶谱定义与计算
信号的高阶谱是功率谱的推导和发展,由维纳-辛钦定理可以得出信号的自相关函数,对其做傅里叶变换,即可得信号的功率谱。所以,信号高阶累积量的傅里叶变换,可求得信号的高阶谱。对一个平稳过程的m阶累积量做m-1维傅里叶变换,即可求得该平稳过程的m阶谱,其中二阶谱就是功率谱。
假设随机变量x的概率密度函数p(x),共特征函数可以表示为:

(2)
对式(2)取对数,可以得到随机变量x的第二特征函数:
Ψ(ω)=ln[Φ(ω)]=ln{exp(jωx)}。
(3)
根据定义,k维随机向量x=(x1,x2,…,xk)T的特征函数与第二特征函数可以表示为:
Φ(ω)=E{exp(jωTx)}=E{exp(j(ω1x1+…+ωkxk))},
(4)
Ψ(ω)=lnΦ(ω)=lnΦ(ω1,…,ωk)=lnE{exp(jωx)},
(5)
式中,ω=(ω1,ω2,…,ωk)T。
将随机向量x的第二特征函数定义为随机向量x的k阶累积量,即为随机向量x的累积量生成函数[16]。随机向量x的第二特征函数Ψ(ω)在原点处的k阶导数:
(6)
如果高阶累积量ckx(τ1,τ2,…,τk-1) 是绝对可和的,则k阶累积量谱为:
(7)
式中,信号的三阶谱一般被称为信号的双谱,典型特征之一是它的阶数是高阶谱中最低的。在信号的双谱中,有比较丰富的相位信息,目前,信号双谱是常用的、性能较好的信号处理特征之一。
2.2 信号双谱特征的估计方法
射频信号的双谱特征分析方法可以分为参数化估计法和非参数化估计法。参数化估计法的优势是具有较高的分辨率,但是在泛在电力物联网的通信环境和实际生产环境中,无线设备终端通信过程中的信号模型比较复杂。非参数化估计法的条件比较宽松,只要能够获得一段符合信号长度要求的信号,就可以进行快速傅里叶变换,使非参数化估计法的性能较好,双谱值估计更准确。
非参数化双谱估计法的步骤为:
① 把接收机接收的信号设为x(1),x(2),…,x(N),接收信号的采样率为fs,在双谱区域沿水平方向与垂直方向上的频率采样间隔为:
Δ0=fs/N。
② 将接收机接收的信号平均分,数量为K段,每一段都有M个值,并对每段接收信号的数据集去均值。
③ 计算每段接收信号的样本的离散傅里叶变换系数为:
(8)
式中,λ=0,1,…,M/2;i=1,2,…,K;{y(i)(n),n=1,2,…,M-1}含义是K段接收信号的第i段信号。
④ 对式(8)计算得到的结果进一步处理,对离散傅里叶变换的系数进一步计算,获得它的三阶自相关值为:
Y(i)(-λ1-λ2-k1-k2),
(9)
式中,i=1,2,…,K;0≤λ2≤λ1,λ1+λ2≤fs/2。
⑤ 取K段观测样本的双谱估计值的均值,即为观测样本的双谱:
(10)
式中,ω1=2πλ1fs/N0;ω2=2πλ2fs/N0。
2.3 个体射频信号双谱实验分析
在做个体射频信号双谱实验时,选用nrf24le1作为发射设备,它的工作频段为2.4~2.525 GHz,共126个信道,GFSK调制,传输距离可达150 m。当SNR=10 dB时,采集2个nrf24le1设备发射的射频信号,按上述双谱估计法计算得到信号双谱,其幅值等高线如图1所示。从图中可以分析得出,2个信号双谱幅值等高线图含有丰富的信息,并且有明显的不同,这2幅图的对比可以从实验仿真角度论证,只要无线设备终端不同,即使它们的型号相同、厂家相同,它们的发射信号双谱特征也不相同。所以,不同无线设备终端信号的双谱图在理论上能够成为射频指纹特征,并应用于电网无线设备的识别和分类。同时,双谱特征具有时移不变性,可以保持信号的幅度和相位不变,并能降低加性高斯噪声的干扰。但从图中也可以看出,双谱特征存在一定的问题,第一是双谱值存在大量的冗余,影响分类的时间复杂度和准确率;第二是二维数据直接匹配的工作量比较大,在电网无线设备入侵检测应用场景中,需要尽可能减少检测所需的时间。所以,直接将无线设备终端的射频信号双谱特征作为射频指纹特征是不可行的,必须做进一步的降维处理才能实现电网无线设备的分类识别。

(a) SNR=10 dB第1组设备信号双谱图

(b) SNR=10 dB第2组设备信号双谱图图1 SNR=10 dB 信号双谱图Fig.1 Signal bispectrum diagram when SNR is 10 dB
2.4 基于局部积分双谱的射频指纹特征提取
理论上,射频信号的双谱特征可以对加性高斯白噪声起到抑制作用,目前,主要采用局部积分双谱的方法来提取射频信号的指纹特征。通过积分函数将二维双谱转换为一维双谱,然后再提取相关特征。常见的方法有径向积分双谱、轴向积分双谱、圆周积分双谱、矩形积分双谱和选择双谱等方法[17]
2.4.1 径向积分双谱
RIB的积分路径是双谱平面上任意一条通过原点的直线,通过该积分路径进行离散求和得到的一组数据即为RIB。PRIB(a)是积分双谱的相位,Chandran在文献[18]中第一次提出将它用作射频信号的指纹特征:
PRIB(a)=arctan(Ii(a)/Ir(a)),
(11)

(12)
式中,B(f1,af1)是信号的普通双谱;PRIB(a)的含义是双谱的相位信息,其最典型也是最常用的性质之一是平移伸缩不变性,这使PRIB(a)具有一定的优势,直观表现了信号双谱特征中的变换。但是,它有一个较为严重的不足,即在运算过程中只用了径向积分双谱的相位。一旦相位信息难以区分,比如应用场景中的信号双谱形状相似、大小不同时,基于PRIB(a)的射频指纹识别方案的性能较差。RIB为了解决这些问题,定义为:

(13)
径向积分双谱典型的特点是时移不变性和相位保持性,所以,在实际应用场景中,它能够将双谱分析数据中包含的信号特征信息表达出来,且效果不错。但是,RIB在积分求和时,会遇到均匀采样的困难,从而使RIB一部分值被遗漏或者重复利用,导致设备分类识别准确度降低。
2.4.2 轴向积分双谱
轴向积分双谱(AIB)是通过将双谱平面上任意一条平行于ω1或ω2轴的直线作为积分路径进行离散求和得到的一组数据,定义为:
(14)
(15)
2.4.3 圆周积分双谱
圆周积分双谱是在双谱平面上以原点为圆心的一组同心圆的积分,表示为:
(16)
式中,Bp(a,θ)是B(ω1,ω2)的极坐标形式,当θ的值取为kπ/2时,Bp(a,θ)的相位信息非常少。因此,需要引入加权圆周积分双谱来解决上述不足,定义为:
(17)
式中,θ的值为kπ/2时,圆周积分双谱的加权系数w(θ)的值比较小,从而使射频信号在计算圆周双谱时具有尺度变化性,并可以在多方向计算积分双谱,提高了双谱信息含量。
2.4.4 选择双谱
颜森(1986)指出,吉安方言属于赣语吉莲片,吉莲片的主要特点是没有入声,而全省其他地区一般都有入声,吉莲片古入声清声母字归阴平,浊声母字归去声。而油田镇地处新余市与吉安市交界之处,而新余话属于赣语宜萍片,宜萍片有入声,且入声不分阴阳,声母送气影响调类分化。油田话发音方式沾有新余话些许特征,较为特殊。因此,在选择发音字表上,单字调分为五类,阴平,阳平,上声,去声和入声。每一个调类选取13个单字,所有的单字都为日常常用字。

i≠j,
(18)

选择双谱的性能较好,它比上文所述的3种局部积分双谱都有优势,轴向积分双谱的缺点是相位信息缺失,径向积分双谱的缺点是尺度变化性缺失,圆周积分双谱的缺点是,在积分的过程中丢失部分特征频点,同时,有一些频点还被重复使用。
2.4.5 矩形积分双谱
矩形积分双谱是采用以双谱原点为中心的一组正矩形为积分路径进行离散求和的数据,定义为:
SIB(ω)=∮S1B(ω1,ω2)dω1dω2,
(19)
式中,S1为矩形积分路径。矩形积分双谱就规避了圆周积分双谱的缺点,同时还具有时移不变性,保持了信号的相位信息和尺度信息,从而可以保证在目标识别中获取重要的特征。
对2个nrf24le1设备分别采集20个样本,信噪比为10 dB,分别使用5种局部积分双谱分析方法从nrf24le1设备发射的信号中提取了特征矢量,它们在最优鉴别子空间投影如图2所示。
图2(a)是RIB投影,图2(b)是AIB投影,图2(c)是CIB投影,图2(d)是选择双谱投影,图2(e)是SIB投影,红色和蓝色分别代表2个不同的nrf24le1设备。从图2中可以看出,当有高斯噪声存在时,由SIB和选择双谱特征提取方法所提取的射频指纹特征矢量比RIB,AIB,CIB提取的射频指纹特征矢量具有更良好的类别区分能力。

(a) RIB投影

(b) AIB投影
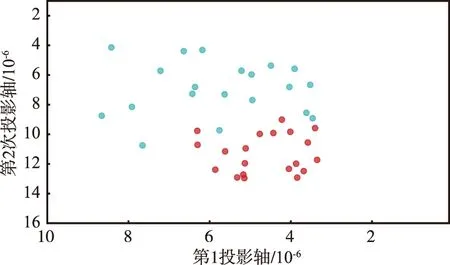
(c) CIB投影

(d) 选择双谱投影

(e) SIB投影图2 RIB,AIB,CIB,选择双谱,SIB投影Fig.2 RIB,AIB,CIB,selected bispectrum,SIB projections
2.5 SIB和选择双谱的融合特征
通过对上述5种射频信号的双谱特征分析,RIB,AIB,CIB和SIB的共同点是在信号的双谱平面中提取特征,不同点是它们在计算时采用了不同的积分路径,而选择双谱采用了信号双谱间的可分离度作为特征参数。综合上述分析,本文设计了一种新的射频指纹特征——SIB和选择双谱的融合特征,该特征直接利用信号的双谱数据保证了时移不变性、相位保持性和尺度变化性。该融合特征充分合理利用了双谱各个频点的值,保证了信息的提取,因此,能够较为准确地提取设备的指纹特征,提高电网无线设备的识别准确率。
3 支持向量机分类算法
SVM是一种常见的分类器[19]。它在解决小样本和非线性识别的问题上性能较好。许多研究资料表明,SVM可以获得全局最优点,解决了神经网络分类算法中局部极值的问题。SVM在应对样本有限的问题时,其目的是得到已有数据样本下的最优解,而不是样本量接近无限大的最优解。
3.1 间隔与支持向量
当给定训练样本集D={(x1,y1),(x2,y2),…,(xm,ym)},yi∈{-1,+1},下一步的目标是在整个样本空间中寻找一个划分超平面,可以通过这个划分超平面区分所有的类别,这是分类识别的原则。
在一个样本空间中,超平面可以描述划分为:
wTx+b=0,
(20)
式中,w=(w1,w2,…,wd)含义是法向量,它是超平面划分的方向;b含义是位移项,几何意义是指原点和划分超平面的距离。
假设超平面(w,b)可以正确区分所有不同类别的训练样本,令:
(21)
支持向量定义为距离超平面最短且可以使式(21)中的等号成立的训练样本。2个不同类别的支持向量到超平面的距离之和是:
(22)
式中,γ即为间隔,寻找满足式(22)中的约束参数w和b,使γ最大,即为最鲁棒的划分超平面:
s.t.yi(wTxi+b)>1,i=1,2,…,m。
(23)
3.2 核函数
间隔与支持向量只能解决训练样本线性可分的情况,在实际的分类应用场景中,原始样本空间一般不存在一个可以正确划分样本的超平面。为了解决该问题,就需要特征空间升维,在更高维特征空间来解决问题。如果直接将样本集的特征映射到高维特征空间,计算量会非常繁琐,极大影响分类的效率。因此,需要使用核函数做转换。核函数的目的是用β(x)代替转换之后高维空间里的特征向量。在高维的特征空间中,划分超平面的表达式为:
f(x)=wTβ(x)+b,
(24)
式中,w和b是模型参数。可以将寻找最佳超平面的问题转化为:
s.t.yi(wTxi+b)>1,i=1,2,…,m。
(25)
核函数的引入,解决了原本特征空间中训练样本线性不可分的问题,同时使算法的复杂度与样本维数二者相互独立,解决了特征维数的问题。
4 实验系统设置和评估
4.1 实验系统设置
本文的实验环境主要包括:Tektronix RSA6114、nRF24LE1和计算机。频谱仪采用Tektronix公司的RSA6114,工作频率为9 kHz~14 GHz。nRF24LE1工作在2.4~2.525 GHz的ISM频段,带有金属屏蔽罩,抗干扰性能强。计算机主机采用Intel(R) Core(TM)i7-4710MQ CPU,装有MATLAB和开源的软件无线电开发工具GNURADIO。
为了检验本文提出的将SIB和选择双谱的融合特征作为射频指纹特征的可靠性和准确率,首先,将10个nRF24LE1设备作为发送端,通过SMA线与频谱仪Tektronix RSA6114连接,这样能保证较为纯净的通信环境,发送端的发射频率和接收端的接收频率均为2.46 GHz,发送端和接收端的采样率均为125 000点每秒。其次,将在这种环境下接收到的信号作为基础信号,如图3所示,左侧是该设备采集的全部样本,右侧是该设备样本集中其中一个样本,通过MATLAB中的AWGN函数叠加噪声,进一步提取SIB和选择双谱的融合特征作为射频指纹特征。最后,使用SVM分类器,在信噪比不同的情况下和信号采样长度不同的情况下分别讨论分类识别准确率。

图3 射频信号采样Fig.3 RF signal sampling
4.2 实验结果和模型评估
对于每个发送端设备均采集了相同数量、相同时长的信号样本,完成信号采集后,分别加入2,4,6,8,10,12,14,16,18,20 dB的白噪声。首先针对每个信噪比下,采样点数为200 000的信号,使用SVM分类算法进行分类,记录不同信噪比下的分类准确率,如图4所示。

图4 不同信噪比条件下的识别准确率Fig.4 Recognition accuracy rate under different SNR conditions
由图4可以看出,本文提出的SIB和选择双谱融合特征作为射频指纹的方案显著优于以稳态信号常规参数作为射频指纹的方案,单独使用SIB和选择双谱作为射频指纹也优于其他局部双谱积分。在信噪比为20 dB时,准确率高达97.1%。
当信噪比为20 dB时,信号采样点个数5 000~200 000的准确率对比,如图5所示。当训练样本为采样点数40 000的信号时,基于SIB和选择双谱融合特征的射频信号识别方案的准确率已经达到90%以上,随着训练样本的采样点数增加,准确率越来越高,说明训练样本集的构成也对无线设备终端的分类识别准确率有较大影响。在与其他各类射频指纹的识别方案比较中,本文提出的基于SIB和选择双谱融合特征的射频信号识别方案仍然保持了优异的性能,进一步证明了方案的有效性。

图5 SNR=20 dB时,不同采样点数情况下的识别准确率Fig.5 Recognition accuracy rate under different sampling points when SNR is 20 dB
5 结束语
在电网无线设备入侵检测的应用场景中,提出了一种基于SIB和选择双谱融合特征的射频指纹识别算法,设计了无线设备检测的方案。本文算法采用了局部积分的双谱特征,避免了大量冗余的运算。实验结果显示,SIB和选择双谱对于信号的区分度最好,在不同信噪比环境下,提出的基于SIB和选择双谱融合特征的射频指纹识别算法都比使用传统稳态信号特征的算法识别准确率更高,同时也优于使用单个局部双谱积分特征的算法。同时,本文算法在信号采样点数偏少的情况下,性能良好,能够有效应对实际环境中复杂多变的情况。
由于现在使用SVM作为分类模型,数据处理阶段需要计算信号双谱特征,运算时间较长。后续考虑使用边云协同的处理流程,通过边缘端与云端的分离和协同,减少计算量,降低本地边缘端的算力要求,进一步优化电网无线设备入侵检测的处理流程和提升识别准确率,更好地服务于泛在电力物联网场景。
