一种战时医学装备维修任务优化调度的方法

舒子芳，向 逾，黄 飞，徐太祥

（1.重庆市巴南区人民医院普外科，重庆401320；2.重庆市巴南区人民医院总务科，重庆401320；3.重庆市巴南区人民医院医学工程科，重庆401320；4.陆军军医大学大坪医院医学工程科，重庆400042）

0 引言

现代化战争中高、精、尖武器的应用使得战斗人员的伤亡数量比以往高出很多，在很大程度上要求战地医疗救治必须快速而高效，因而提供后勤保障的医学装备维修成为伤员得到紧急救治的重要条件之一。面对或将出现的大面积救治群体及不确定因素，不可能按照平时后方医院的条件大量配发医学装备或足量附件，只能依靠维修小组在战场需要的地方进行应急维修与装备更迭。在分布较广的战斗区域，因战损直接导致维修工作呈现多样化特征[1]，其维修时间与效率成为关注焦点，可以说一个正确的维修支援调度决策直接关乎伤员的伤情，这就对维修保障的调度能力提出了严峻的挑战。

在战斗过程中，各类各级装备的维修力量非常有限[2-3]，而维修任务可能远远超过其数量，同时维修任务的开展由后勤决策部门统一研究决定。因此，有必要针对战时医学装备维修的主要特点和现实需求对维修小组的科学调度进行研究，确保调度决策的正确和高效，避免出现资源配置过剩或不足的问题，以期提升我军对战时医疗救治的保障能力。

1 战时医学装备的维修特点及排队调度模型

1.1 维修工作特点及研究现状

战时医学装备的维修具有时空分布广、难易程度不一、支援路线复杂等特点，其范围涉及一线战地医院、后送运输载体（救援方舱、卫生列车、卫生飞机等分类集中救治单元）及后方医院。从列装装备的复杂度来看，战地医院的维修难度最低，后方医院最高；从紧急程度来看，一线战地医院最为迫切。故维修调度系统整体上应体现以需求和保障效能的匹配度为核心的任务调度模式。目前，部队暂未对医学装备维修提出相关调度方案，仅能参考“先来先修、重要装备优先”[4]的武器装备维修调度纲领，但这难以实现缩短等待时间、按需优先保障、以最小时间成本满足战场总体医疗救治的目的。

在理论研究方面，王强等[5]提出阈值连续变化条件下的军事装备预防性维修判断法，但该方法无法应用于任务调度。张守玉等[6]基于占线排序理论研究装备维修策略，这仅属于多选一的策略优选研究。张宏铭[7]提出了粒子群优化算法，提高了调度的效率，但该方法对离散问题的优化处理不佳，容易陷入局部最优。高建军等[4]重点利用静动态调度模型对武器装备的各项参数进行加权分析以确定维修紧迫度，但只假设了单个维修队且未讨论优先级规则。

1.2 排队模型描述

战时的维修机构、待修故障设备、配件保障供应等要素之间均具有离散的随机属性。面对有限的服务资源，可能存在任务量与服务资源不匹配的情况，当需要维修的任务量超出了维修部门的容量，就可能出现排队待修的问题[8]，而这样的排队并非简单的先进先出模式。上述服务机构和服务对象形成了一个排队（又称随机服务）系统，如图1 所示。

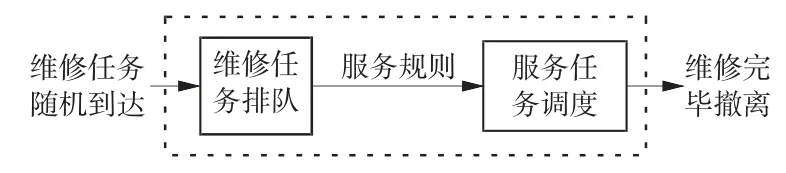
图1 维修任务排队模型框图

图1 中战时维修任务的到达过程可能有以下不同情况：（1）任务到达可以是批量的，也可以是单独的；（2）任务的数量可以无限，也可以有限；（3）任务相继到达的间隔时间分布及其数学期望、方差等数字特征都可能与时间存在相关性或不相关性[9]。任务排队是指到达排队系统的任务按怎样的方式排队等待，主要有损失制和等待制。损失制：当任务到达时，若所有的服务均被占用，任务随即取消。等待制：若任务到达时所有的服务均被占用，任务就排队等待，直到接受完服务才离开，医学装备的排队待修就属于这种情况。

图1 中服务规则有4 种：（1）先到先服务（firstcome first-served，FCFS），不分轻重缓急，按任务到达的先后顺序实施调度；（2）后到先服务（last-come firstserved，LCFS），类似于货物出库的后进先出，这不适用于维修调度；（3）随机服务（random service，RAND），不考虑维修任务的难度或者重要性，随机指派维修力量，但易出现对象与服务不匹配的问题；（4）优先权服务（priority right，PR），将高优先级赋予等待成本较高的任务，又分为非强占优先服务和强占优先服务。

1.3 调度模型描述

维修任务调度作业包含以下过程：任务到达维修部门—根据故障情况做好维修评估与计划—维修小组进驻维修—撤离，调度过程中任务不能临时取消，最终结果只有修复与未修复。撤离后重新空闲的维修队伍再次参与调度，如此循环往复，形成一个闭环的维修任务处置网络。

根据实战模拟分析，调度模型可定义为：

（1）战斗中装备可能反复出现故障，故维修任务数量可认为是无限的，任务之间以及任务的到达时间是基本相互独立的，任务到达的数量只与某时间区间的长短有关，因此维修任务的到达属于泊松分布。

（2）维修任务到达时间随机，其相邻任务的时间间隔属于随机变量，且服从负指数分布。

（3）同等优先级的故障装备采用先到先修的规则。

（4）任务调度的规则选用非强占优先，即一旦维修小组派出，本次调度就不能被打断直至维修结束。

（5）派出维修小组的能力与维修任务的实际需求基本匹配，各组平均维修率可视为相等。

综上所述，假设维修部门实施多路维修小组调配、非强占优先的调度规则，则排队模型可记为M1/M2/c/∞/m/PR，其中，M1表明维修任务相继到达的间隔时间为指数分布；M2表明维修力量的服务时间为指数分布；c指战区内部署维修服务小组的数量，c∈N；∞指可接纳维修任务的数量为无穷大；m指战区内服务对象的数目，m∈N；PR 指模型采用的服务规则。

2 优化调度模型建立

2.1 基本参数计算

在实际业务调度中，各维修小组的任务基本上是互相独立的。若各组的平均维修率μ1=μ2=…=μ，则所有小组的出勤概率共同决定总体维修任务的调度运行状态。设n为待修队列长度，任务平均到达率为λ，战场服务对象m为有限量，且m＞c。若n≤c，表明所有的医学装备都在被维修，则有c-n个维修小组空闲；若c＜n≤m，则有n-c个维修任务排队。排队系统的状态转移如图2 所示。

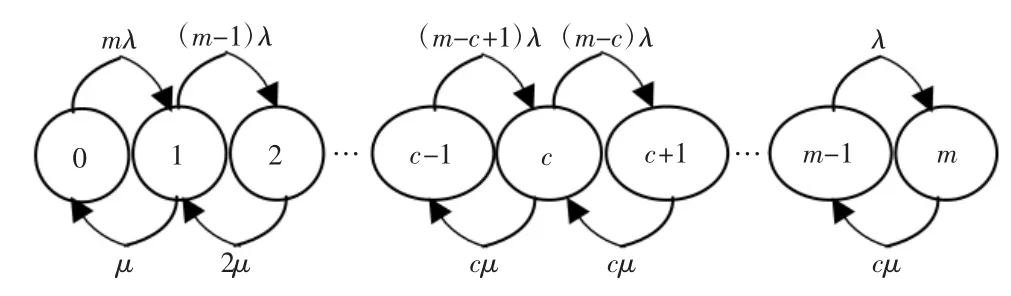
图2 排队系统的状态转移图

按前述设定，状态概率P0为

平均逗留时间Ws为

2.2 排队模型确定

多数情况下，维修小组的数量是少于待修装备任务数的，因此必须提高任务调度效率，降低队列中的等待时间Wq。但首先需要确定任务调度执行的基本模式：单队列并行处理或是多队列并行处理。2 种模式的模型分别为：（1）固定数量c的维修小组，只设定1 个维修任务待修队列，只要有空闲的小组就实施调度，如图3 所示；（2）维修任务划分为若干组并同时分配给所有维修小组，各个小组并行接收不同的维修任务，只要某个维修小组空闲，其对应的任务就能被处理，如图4 所示。

图3 单队列并行处理模型(c＜m)

图4 多队列并行处理模型(y＜t≤m，c＜m)

若维修部门有c=5 个维修小组，战损医学装备有m=10 个任务并服从λ=0.4 的泊松分布，各个小组的平均维修率μ=0.6。下面分别对5 组每组2 个任务的多队列模式和1 组每组10 个任务的单队列模式的参数进行计算，结果详见表1。

表1 不同模型的参数计算结果

由表1 数据可知，只有1 个队列的M/M/5/∞/10模型的平均等待时间较短，系统综合效率较高，空闲率较低，等量任务下完好率较高，具有较明显优势，因此在战时任务调度时可选用图3 所示模型。

2.3 优先权规则下的排队模型

基本排队模型选定后，需要进一步检验M/M/c/∞/m/PR 模型优先级规则的可行性。当具有优先权的任务到达时，若未出现服务空闲，由于是非强占规则，它不能强占在用服务资源，且只能排在比它优先权级别更低的任务前面排队等待服务。可以认为：同级优先权任务中，只有缩短平均等待时间能使其他任务在队列中的等待成本最小，同时使较高优先级任务的平均等待时间更低，且调度系统对每一类任务的平均维修率是确定的和相同的，这样才能缩短优先级更高或者需求更紧迫任务的等待时间，从而为总体调度工作节约时间成本。维修任务的优先级（不考虑路途和敌对危险因素）划分详见表2。

表2 优先等级的示值及含义

若到达排队系统的是第1 级任务，它具有的平均等待时间包括2 个部分：队列中等待的全部第1级任务平均服务时间之和以及等待服务空闲的平均时间。该级等待维修的医学装备平均数为Lq1，S为系统的服务时间，则系统平均服务时间S¯=E（S），E（S）表示对S的期望。首先，本级所有待修装备占用的平均服务时间总和[11]S¯1Lq1可表示为

式中，μ1为第1 级任务的平均维修率，ρ1为第1 级任务的工作强度，Wq1是第1 级任务的平均排队等待时间。Wq1计算公式如下：

其次，设新到任务具有第z级优先权，则其等待服务空闲的平均时间由3 个部分构成：

（1）正在排队的第1～z级任务的平均服务时间之和T1，计算公式如下：

（2）等待正在维修的维修小组空闲出来的平均时间T2，计算公式如下：

式中，为平均剩余服务时间。

（3）在第z级任务排队等待期间，后续到达的第1～z-1 级任务优先调度形成的平均耽误时间之和T3，计算公式如下：

3 案例分析与结论

边境某战场，共有m=50 处固定式或移动式救援医疗点，按照装备战损程度分为3 类任务（一般任务27 处，比较紧急任务15 处，非常紧急维修任务8 处），均为泊松到达，到达的任务均接受初始化排队，且已知平均到达率λ=0.4 处/h，平均维修率μ=0.6 处/h，要求保证平均完好率η≥90%。由公式（8）可知，无故障的医疗点至少有45 处，平均故障数量队长Ls的最大值为5，其余结果详见表3。

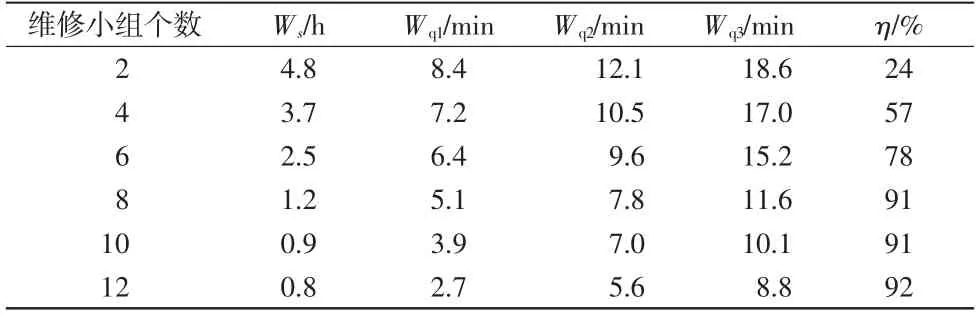
表3 维修任务调度案例的计算结果

由表3 数据可以得出：（1）一定区域内的维修小组并非越多越好，完好率在达到91%后基本处于稳定，说明8 个维修小组即可满足预定要求，空闲服务已趋于饱和，这为后勤部门准确计算或配备合理维修力量提供了定量参考。（2）在横向比较上，越高优先级任务的等待时间Wqi呈现出越小的特征，说明享有较高优先级的任务能越快被响应，同时随着维修小组数量的增多，其值也纵向减少，因此实现了优先级调度决策。（3）维修小组在数量较少的情况下，完好率只有不到1/3，服务机构严重不足导致等待时间差别较大，而每递增2 个小组均能有效缩短相同优先级任务的平均等待时间，同时还能提升完好率，因此维修小组的数量在调度决策中具有重要影响。（4）该优化调度决策方案能减少不增值的资源浪费与维修小组负荷过重之间的不匹配，以非强占优先级规则降低了等待时间过久带来的伤亡损失，以兼顾效率的方式缩短了任务的平均逗留时间，用较少的排队时间赢取了关键的医治时间，具有一定的现实可行性和积极意义。（5）排队论可以解决类似任务调度的随机离散性问题，同时利用优先权规则实现对目标函数的数学期望最优。

4 结语

卫勤保障中的医学装备维修调度如何满足战时医学救治需求是一个影响我军综合战斗力的重要课题。对我军维修部门而言，总是希望以有限的维修力量、较短的排队等待时间或者等待队长来满足战场循环不断的医治需要。因此，本文利用排队论的函数分布规律对离散随机的维修调度系统进行数学建模，分析了维修任务的战时数字特征，模拟符合实情的假设条件，比选了更为合理的排队模型，提出适合战场环境的服务规则，并围绕排队理论中的主要评价指标建立优化调度模型，解决了离散信息的动态优化问题，从缩短等待时间的角度达成需求与维修力量的动态平衡，为部队保持最佳的维修调度效率理清了思路。

战场装备维修任务本身可以认为存在稳态情形，其保障效能可以按平均等待时间来衡量。有的武器装备可以暂缓维修，但伤员不能暂时不救，重要战地更需要优先支援[12]，因此医学装备的维修任务调度具有更强的时效性、针对性和实用性。只有通过实现优先级调度才能加大维修任务的有效执行密度，提高整体运转效率，弥补无差异化“先到先修”方案带来的决策弊端。医学装备维修任务的调度应当按照一定的规律灵活、合理地配置才能使有限的维修力量发挥更大的作用。综上，排队论有利于降低平均等待时间和提高总体维修效能，可为战时医疗救治争取宝贵时间。