引信参数变化对装定性能的影响

魏亚伟，李豪杰，余春华，原红伟，黄 虎

(1.南京理工大学机械工程学院，江苏 南京 210094; 2.陆军装备部驻北京地区军代局驻长治地区军代室,北京 102202)

0 引言

新形势下战争不再是单一的某一个作战单元发挥作用去攻击敌方，而是与其他的作战平台交联成一个整体，实现信息交互[1-3]。引信装定技术是实现信息交互的基础，其中引信有线装定因其制造工艺简单、结构能够合理安排、功耗小、具有较高的稳定性等优点，是目前国内外引信装定的主要手段之一。在有线装定过程中，装定快速性包括两个部分：信息装定的快速性和能量装定的快速性。文献[4]提出了身管炮膛内有线装定构想；文献[5]对有线装定系统进行了高精度和安全性设计。以上文献仅仅在有线装定功能上提出了构想和完成了实现，并没有对装定快速性的影响因素进行分析研究。目前，对传输线间分布电容计算模型[6-7]以及电缆之间的电阻、电容对系统的影响进行了不少研究[8-9]。文献[10]研究了共线式底火装定电缆对信号传输的影响，得出了影响装定信号传输的两个主要因素是电缆长度和工作环境；但是并未对装定能量的快速性进行分析。

本文主要针对不同的有线装定平台，电缆长度的不同对能量装定快速性造成影响的问题，建立有线装定回路模型，通过Cadence进行仿真，分析不同长度电缆线对装定性能的影响，给定模型及参数条件下，得到储能电容两端电压达到某个压值时，装定性能最优。

1 有线装定技术原理

引信的有线装定是指通过装定电缆线将引信所需的能量，引信的作用时间、作用方式以及技术参数等信息进行传递，以满足引信的作战要求及作战指标。有线装定系统主要由装定器模块、有线装定回路、引信电路模块三部分组成，如图1所示。火控系统将装定信息通过武器系统平台接口传递给装定器，装定器将接收的信息进行调制解调后，通过装定电缆线传递给引信，同时也进行能量的传输。引信接收到装定信息后，根据装定的信息要求，完成自己的任务使命。

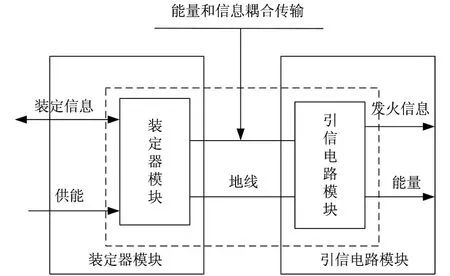
图1 有线装定系统原理框图Fig.1 Schematic diagram of wired installation system

2 有线装定回路的模型构建

有线装定回路电路模型的构建如图2所示。其中Vi是装定器的输出电压，也是信号的输入端；Vo是引信的输入电压；电阻Ri是装定输出回路上的电阻；R1和R2是装定回路中电缆线的阻值，两者的阻值相等；R3为引信模块中的等效电阻；C1为电缆间分布电容与电缆与金属环境之间的感应电容值的和；C2是引信模块内的储能电容，炮弹发射后为引信模块提供能量；Ro为接收电压间的电阻。当装定器和引信电路确定后，Vi、Ri、R3、C2、Ro的值可以确定，而R1、R2、C1的值与电缆的长度以及环境因素等有关。

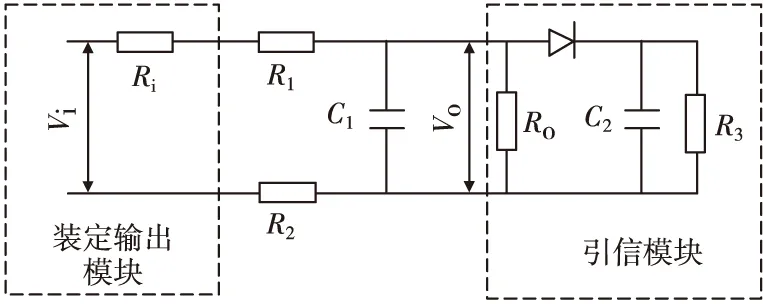
图2 有线装定回路电路模型Fig.2 Circuit model of wired fixed circuit

2.1 有线装定回路中电阻与电容的计算

1) 有线装定回路中电阻的计算

导体的电阻是由其自身条件决定的，选定某种材质的金属作为导体时，其电阻率就是确定值。当横截面积一定时，其阻值仅与长度有关。假设所选电缆导线的横截面积为S，导线长度为L，所选材料的电导率为ρ，则电缆线的阻值为：

(1)

2) 有线装定回路中电容的计算

有线装定系统应用在各种武器平台上时，其上面的金属材料可以看成一块无限大的金属板，此时，不仅两根电缆线之间存在分布电容，电缆线与金属材料之间也会存在分布电容。电力线模型如图3所示，电缆线1和2在金属板3上。电缆线的直径为d，两根电缆线之间的距离用Si来代表，距离为Si的两根导线的长度为Li。当系统工作时，其中一根导线为激励源，这样就会存在两个电容器，分别计算两个电容器的电容。

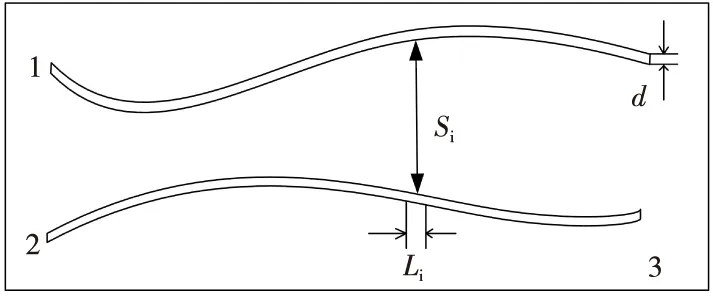
图3 电力线模型Fig.3 Power line model

对于电缆线1和2之间的电容的计算，可以使用平行圆柱形电容器公式进行解决，两根平行导线的直径为d，且相互平行，S为两者之间的距离，且S≫d/2,ε为两个平行导线之间的介质常数，ε0为自由空间的介电常数，通过计算两个导线单位长度的电容值为：

(2)

则导线距离为Si，长度为Li的分布电容值为：

(3)

所以逐步累加可得电缆线1和2之间的分为电容为：

(4)

式(4)中，n=1,2,3，…。

因为电缆间的距离Si是一个随机变量，可以假设服从正态分布Si～N(u,σ2)，电缆线之间的距离的数学期望u为距离的平均值。假设电缆线之间的最大距离和最小距离分别为Smax，Smin。则u=(Smax+Smin)/2。所以两根电缆线之间的分布电容为：

(5)

对于导线与金属板之间的电容，如图4所示，可以把导线看成横截面积很小的极板，则两个极板之间的电容计算方法如下：

(6)

式(6)中，L，d1为电缆线的长度和直径；S1为电缆线到金属板的距离。

图4 导线与金属板之间的电容示意图Fig.4 Capacitance diagram between conductor and metal plate

式(5)和式(6)中均含有相对介电常数ε和自由空间的介电常数ε0。不同的导体介质对应了不同的介电常数，介电常数对电容的大小也会产生影响。当工作的环境确定下来时，介电常数就是一个定值，此时，电缆之间的分布电容主要受电缆长度影响。表1中是一些常见的物质介电常数。

表1 常见的物质相对介电常数Tab.1 Relative permittivity of common substances

2.2 有线装定回路参数对储能电容的充电特性的影响

1) 根据图2模型的构建，当充电完成时，储能电容两端的电压为Vo，则：

(7)

2) 充电电路的总电容和总电阻分别为：

C=C1+C2

R=Ri+R1+R2

根据RC电路的充电公式：

Uc=Uoexp(-t/RC)

储能电容两端电压随时间的变化公式为：

(8)

式(8)中，τ为充电电路的时间常数：

3 仿真分析

有线装定系统一般的工作环境是在空气中，所以相对介电常数ε=1；真空介电常数ε0=0.089 pF/cm；装定电缆线的半径d=1.38 mm；电缆线到金属极板的距离为S=0.69 mm,所选电缆线为铜材料；电阻率ρ=1.75×10-8Ω·m；装定电缆线1和2之间的最大距离dmax=10.5 cm,最小距离dmin=0 cm。其中Ri=16 Ω，C2=200 μF。所以得到：

τ=(3.17×10-9L2+0.032 8L+3.2) ms

(9)

由图5可知，二次项系数过小，基本可以忽略不计，时间常数τ与电缆线长度L成正比关系。

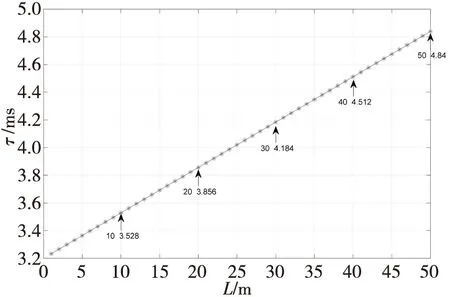
图5 储能电容时间常数随电缆长度变化示意图Fig.5 Schematic diagram ofenergy storage capacitance time constant changing with cable length

利用Cadence中Pspice仿真工具进行电路仿真，如图6所示。

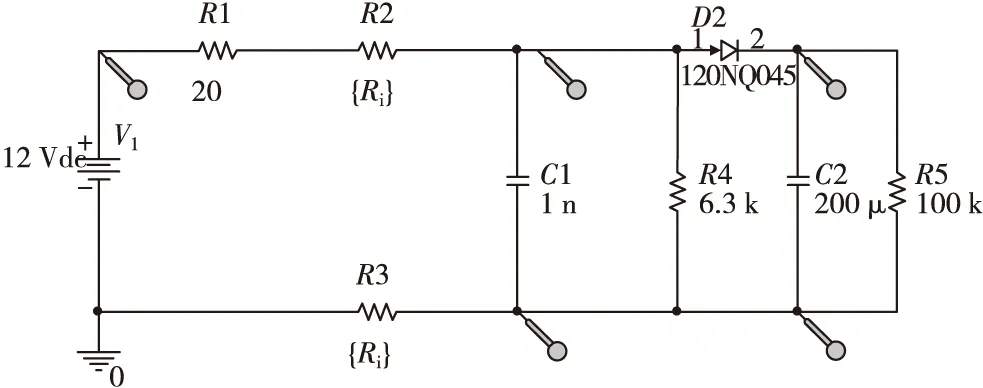
图6 电路仿真示意图Fig.6 Circuit simulation diagram

如图7所示，从左到右有5条储能电容充电的曲线，依次取电缆线长度为10、20、30、40、50 m。从图像可以看出电缆线长度越长，充电曲线变得越缓慢，充电速率变慢。由式(9)可知，电缆每增加10 m，增加的时间常数Δτ=0.328 ms，根据电容充电规律，充电量为98%时，所增加的时间为4Δτ=1.312 ms。

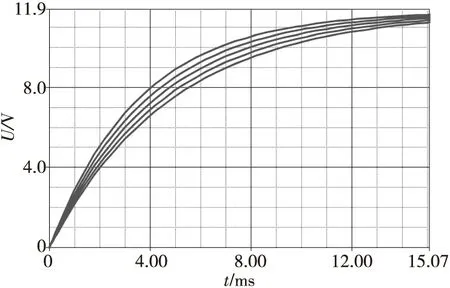
图7 不同电缆长度的储能电容充电曲线Fig.7 Capacitance charging curve of different cable lengths

在实际的工作电路中，当储能电容两端电压充到10 V左右，装定系统进行信息装定。对于一般的TTL和CMOS电路芯片，工作电压一般在5 V左右，如果电容两端电压达到负载模块可以稳定工作时的电压，装定系统开始装定，可以明显提高装定速度。不同电缆线长度时储能电容两端电压分别达到6、10 V所需要的时间如表2所示。

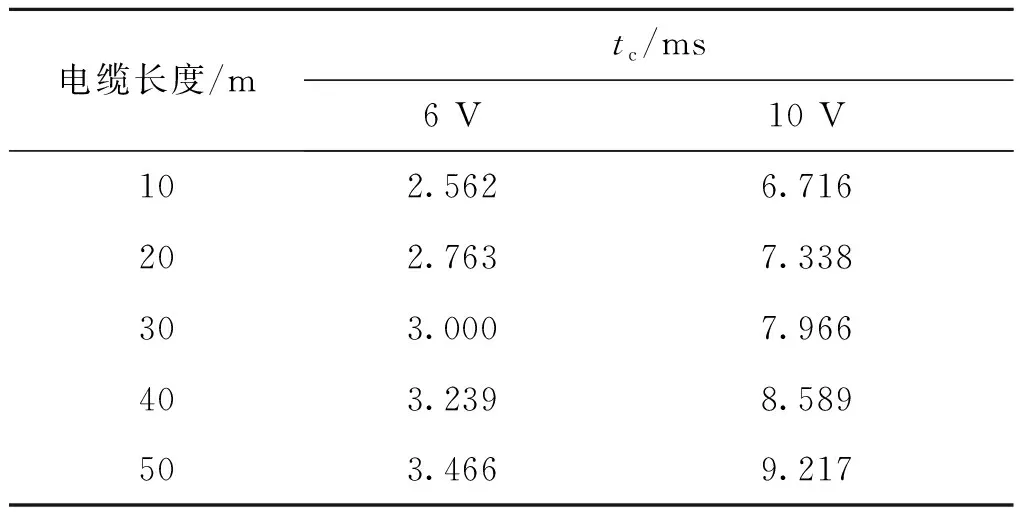
表2 储能电容充到特定电压所需时间Tab.2 Time required for capacitor charging to specific voltage

通过Matlab对表2数据进行拟合，拟合的结果如图8所示，储能电容两端电压从6 V到10 V所用的时间与电缆线长度成正相关，当电容两端电压达到6 V时，装定系统开始装定，10 m电缆时缩短的时间为4.154 ms，50 m电缆时缩短的时间为5.75 ms。

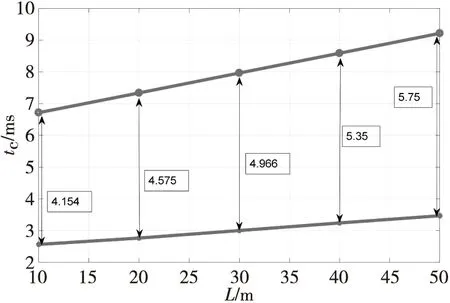
图8 不同电缆长度时储能电容充到特定电压所需时间的拟合曲线Fig.8 Fitting curve of the time required for the charging capacitor to be charged to a specific voltage at different cable lengths

根据式(7)和电容充放电规律可知：

(10)

式(10)中，Ct为储能电容当前充电量占充满时电量的百分比。当充电时间t=τ时，Ct=63%；当t=2τ时，Ct=86%；当t=3τ时，Ct=95%；当t=4τ时，Ct=98%。

图9是30 m电缆线时的储能电容充电曲线图，由图5可知，该电容的时间常数τ=4.184。

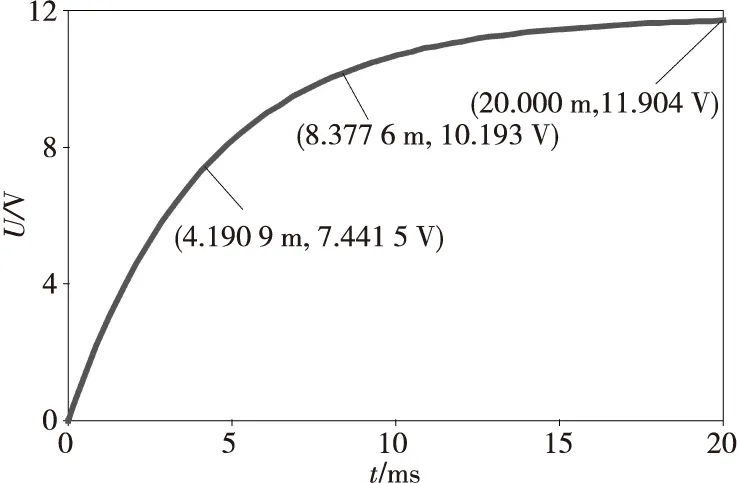
图9 30 m电缆线时储能电容充电曲线Fig.9 Charging curve of energy storage capacity in 30 m cable

由图9标记处知当t=τ时，电压为7.441 5 V，当t=2τ时，电压为10.193 V，充满时的电压为11.904 V。所以当t=τ时，7.441 5/11.904=0.625=62.5%；当t=2τ时，10.193/11.904=0.856=85.6%。

通过仿真计算，不同时间下储能电容的充电量和理论值基本相等，仿真的数据真实可靠。

4 结论

本文对引信有线装定过程中装定参数变化对装定快速性影响的问题进行了研究，推导了不平行电缆间以及电缆与坦克车金属板间分布电容的表达式。通过理论计算和模拟仿真，影响装定能量快速性的主要因素是电缆长度。相同环境下，储能电容充电到额定电压的98%时，电缆长度每增加10 m，所需的时间增加1.312 ms。给定模型及参数条件下，给出不同装定电缆时储能电容充电到10 V与6 V的时间，与充电到10 V相比，充电到6 V时10 m电缆时缩短的时间为4.154 ms,50 m电缆时缩短的时间为5.75 ms,对提高装定快速性具有重要意义。最后通过30 m电缆线时电容充电特征值与理论值进行比对，两者数值基本相等，仿真的数据真实有效。