基于OFDM的多载波相位定距算法
2021-05-08范兵兵徐立新杨佳捷
范兵兵,徐立新,杨佳捷
(北京理工大学机电学院,北京 100081)
0 引言
无线电引信是一种利用目标对发射电磁波的反射特征求解目标距离信息的引爆装置,作为精确制导武器系统末端的组成部分,决定了引信系统整体的作战效能。导引一体化与智能弹药的发展趋势要求未来引信不仅要具备基本的探测能力,还需有一定的通信能力,这些传统意义上的探测体制难以满足这一要求。基于软件无线电(SDR)平台的引信系统以算法通用性强、抗干扰能力强、易于升级维护等特点得到了越来越多的关注[1]。在无线通信领域,基于正交频分复用(OFDM)的无线电通信系统已经广泛应用到了数字广播、无线局域网以及第五代移动通信系统中,其在软件无线电引信上的应用满足了引信智能化、网络化的发展需求,具有重要的研究意义。
OFDM是多载波信号传输方案中的一种, OFDM定距是无线传输系统中的一种无线定位技术,其相邻子载波的频率间隔较小,具有较高的频谱利用率[2]。文献[3]首先提出了多载波探测系统设计方案,从多频角度精确计算了信号的到达时间进行距离估算。文献[4]在基于OFDM技术的基础上提出了伪码定距和相位定距相结合的定距算法,通过相关处理获得最大不模糊范围,通过相位测量获得更小的距离分辨率。文献[5]研究了基于OFDM的多载波雷达在测量高速目标时的性能仿真。文献[6]设计了基于OFDM的应答式雷达的硬件平台,它通过联合多个载波相位差信息进行距离估算。OFDM相位定距技术在雷达定距方面日趋成熟,本文在上述论文的基础上,针对相位定距过程中最大不模糊距离和定距精度这一矛盾,研究了基于OFDM的多载波相位定距算法在软件无线电引信上的应用。
1 软件无线电引信探测系统
软件无线电引信以通用硬件平台作为引信的基础,通过不同的软件编程重新配置硬件参数实现各种不同体制引信所需要的功能,其硬件结构决定了引信系统的兼容性、开放性和可升级性。
1.1 软件无线电系统硬件平台
本文系统硬件平台采用了一次下变频的宽带中频带通采样软件无线电结构,该结构框图如图1所示。这种架构硬件和超外差式无线电平台类似,硬件平台根据功能分为两个模块:FPGA信号处理模块和AD9361射频模块。AD9361射频电路的硬件参数可以通过FPGA进行软件重配置,采用此方案的系统可以灵活选择射频工作频段、发射信号带宽,对接收信号能进行实时数字化信号处理。
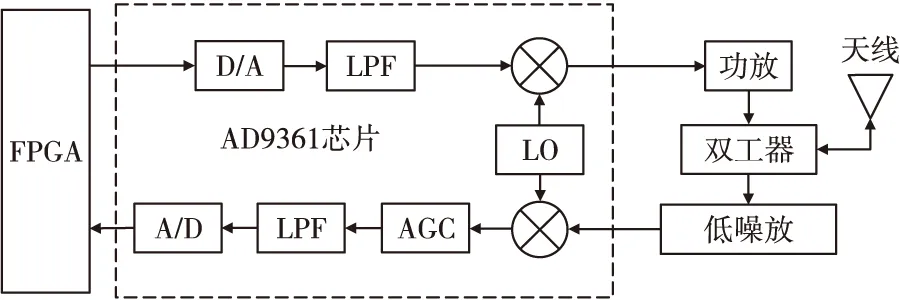
图1 软件无线电硬件平台结构图Fig.1 Structure of software radio hardware platform
FPGA数字信号处理模块的功能包含三个方面:产生多条载波复合的发射信号、进行AD9361芯片的配置和回波信号处理。射频模块主要的工作是完成信号的收发,其硬件组成包含了收发天线、低噪声放大器、功放、SMA接口、巴伦和AD9361芯片。AD9361是一款射频捷变收发芯片,主要的工作是完成接收与发送的中频信号处理,数字信号与射频信号的转换,芯片内部功能如图虚线框所示,其信号处理完成了混频、滤波、抽取、放大、A/D和D/A转换等。
相比于传统相位定距引信,该硬件平台在射频端多了信号上下变频的过程,回波信号多了两项由射频本振引起的相位变化。受制于AD采样的限制,数字端信号最大传输速率为61 MHz,信号最大带宽为30 MHz。
1.2 多载波相位定距算法原理
多载波相位定距算法与传统相位定距算法相比,能够同时利用多个频率的相位差,在提高定距范围的同时,又保证了定距精度。OFDM是目前最典型的多载波技术,它通过多个相互正交的子载波能够同时发射多个信号并且准确解调,丰富了收发信号的信息量。系统的发射信号为N个相互正交不重叠的子载波的叠加,本次发射信号以子载波基频为相邻子载波之间频率间隔,数字端发射信号St的函数表达式为:
(1)
式(1)中,N为子载波个数;Bk为第k个子载波的幅度;fb为子载波的基频;φk为各个子载波的初始相位。发射信号经过射频电路上变频发射到自由空间,经过目标反射后的数字端回波信号Sr表达式为[4]:
2π(fc+kfb)τ)
(2)
式(2)中,α为信号的幅度衰减;φt为射频端发射信号由于上变频造成的相位变化;φr为射频端回波信号由于下变频引起的相位变化;fc为射频端载波频率;τ为距离引起的发射信号和回波信号时间差,它和距离的关系为τ=2R/c。
多载波相位差定距算法需要对回波信号进行两次混频处理提取不同频率下的相位差信息。一次混频需要将回波信号与发射信号的子载波进行IQ双通道乘运算,之后经过低通滤波后就能提取出各个子载波的相位信息,一次混频后各子载波Sk为:
Sk_cos(t)=cos(-2π(fc+kfb)τ+φt-φr)
(3)
Sk_sin(t)=sin(-2π(fc+kfb)τ+φt-φr)
(4)
从式中可以看出不同频率的子载波具有不同的相位,不同频率间子载波的相位差只与2πkfbτ有关,相位差和频率差成线性比例关系。通过二次混频完成不同频率下的相位差信息的提取,其运算分为三项:
1) 二次混频和运算:它分别对两个子载波I通道混频(见式(5))和Q通道混频(见式(6)),将两式相加就能获得相位差信息的余弦值(见式(7))。
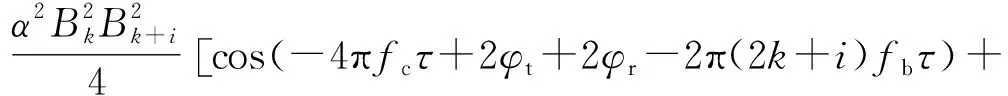
(5)
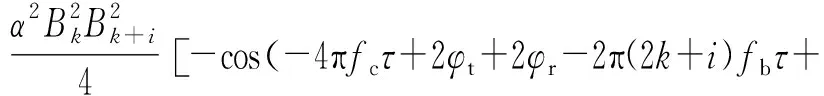
(6)
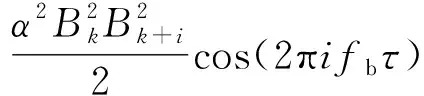
(7)
2) 二次混频差运算:它对两个子载波I通道和Q通道交叉混频,再对两式差运算就能获得相位差信息的正弦值。
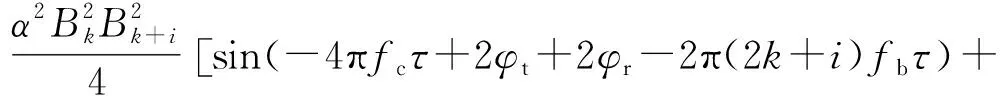
(8)
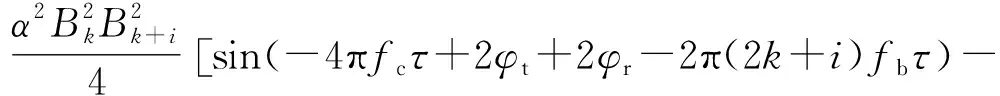
(9)
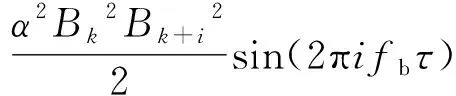
(10)
3) 对相位差信息正弦值和余弦值除运算处理获得正切值(式11),通过反正切计算即可获得相位差信息。
(11)
不同频率下的距离和相位差关系为:
(12)
式(12)中,Δθi为频率为i倍基频时的解算相位差,由于正切函数周期为π,其相位差范围为0~π;m表示相位差的整周期个数,当目标距离大于子载波的最大不模糊距离c/(4ifb)时,就会产生距离模糊现象。在基频为1.25 MHz时,不同频率下的相位差与距离的关系如图2所示,图中分别描述了1倍、2倍、4倍、8倍和15倍基频下相位差与距离的关系。
图2(a)、(b)对应的最大不迷糊距离分别为60 m和30 m,该系统最大探测距离为30 m,此时相位和距离为一一对应的关系。而图2(c)—(e)频率在定距范围内存在多个周期,同一相位对应了多个距离,相位差和距离在周期性范围内具有线性比例关系,直接通过单个相位差定距存在距离模糊的现象。同时对于相同的距离差,在高倍频率时相位变化量大,距离分辨能力强,定距精度高。多载波相位定距信号处理算法利用低频率进行距离解模糊,同时利用高频率进行精确距离计算,有效利用了两者之间的优势。
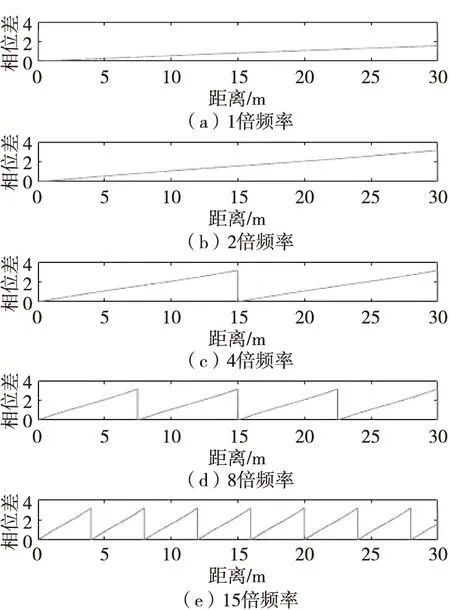
图2 不同频率下相位差和距离的关系Fig.2 Relationship between phase difference and distance at different frequencies
2 信号处理流程与仿真
根据硬件系统参数,发射信号带宽选择为20 MHz,考虑到数字平台信号处理的能力,子载波数量选择为16个,系统基础频率差fb为1.15 MHz。仿真环境下数据处理时钟频率为50 MHz,目标起始距离为30 m,弹目相对速度为1 000 m/s,模拟回波信号的信噪比为15 dB。此时多载波相位定距算法可以同时计算15个不同频率差的相位值,其信号处理流程如图3所示。
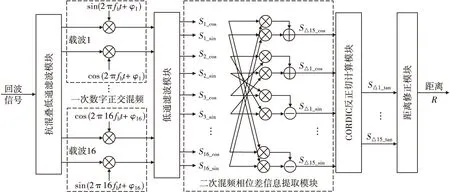
图3 信号处理算法流程图Fig.3 Flow chart of signal processing algorithm
数字端信号处理主要由6个部分组成:首先是抗混叠低通滤波模块,该模块对信号进行抗混叠处理,有效滤除了传输过程中耦合的高频干扰杂波;其次是一次数字正交混频和低通滤波模块,这两个模块从回波信号中提取出各子载波相位信息;之后是二次混频相位差信息提取模块,此模块通过积化和差运算获得多个频率的相位差信息的正弦值和余弦值;然后是CORDIC反正切计算模块,该模块通过移位运算和加运算完成了硬件电路的反正切计算;最后是距离修正模块,该模块利用多个频率的定距值进行距离解模糊和修正以获得精确的距离。
图4为多个频率的定距值,可以看出15倍频率的定距精度要远大于2倍频率的定距精度。同时由于相位差的周期性,其定距结果也存在周期性,并且在各个整数倍最大不模糊距离处存在距离突变的现象,直接采用此定距结果与实际距离相比存在很大的误差。
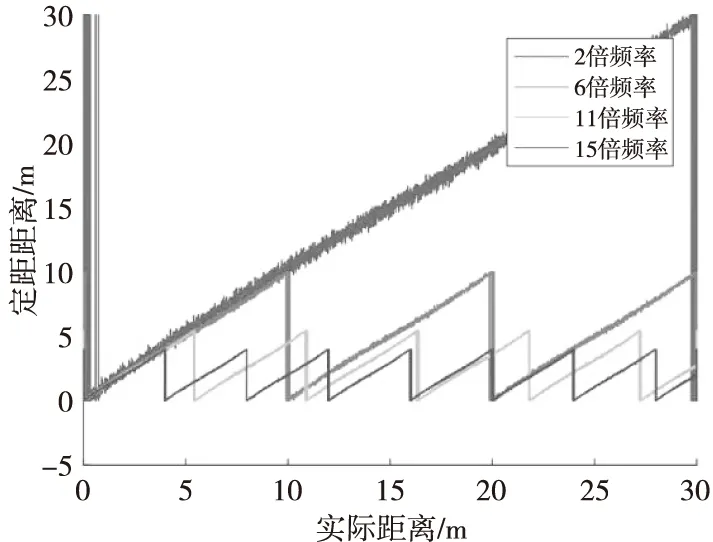
图4 多个频率的定距结果图Fig.4 Ranging results of multiple frequencies
距离修正将利用低频率的定距值估算高频率定距值的距离周期m用来消除距离模糊,同时利用多个高频差定距值互相补偿以消除距离突变处的定距结果的不稳定。该模块处理流程图如图5所示,它对初始定距值进行了三次修正。RΔi为15个频率下的定距值,R1为初始定距结果,R2、R3和R4分别是一次修正、二次修正和三次修正后更精确的定距值。
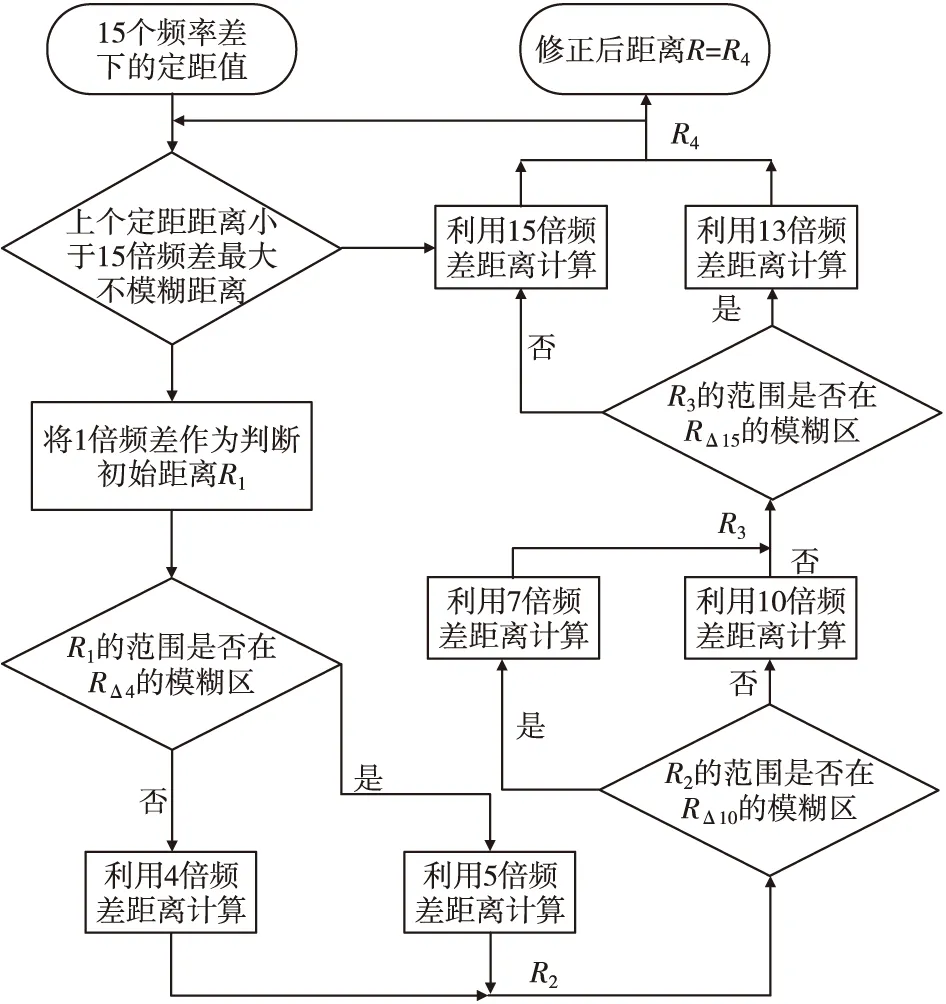
图5 距离修正模块流程图Fig.5 Flow chart of distance correction module
距离修正模块将1倍频率定距值作为初始结果进行距离解模糊。该模块首先判断R1的定距值是否在4倍频率定距值RΔ4的模糊范围内,如果不是则根据R1计算出距离周期,并将15 m+RΔ4作为一次距离的修正值;否则将20 m+RΔ3作为一次距离修正值。同理可得二次修正距离R3为8.6 m+RΔ7或6 m+RΔ10,三次修正距离R4为4.6 m+RΔ13或4 m+RΔ15。当上一时刻的定距结果小于4 m时,则直接将RΔ15作为近距离下的最终定距结果。
图6是距离修正模块R1、R2、R3和R4的各级定距误差仿真结果。仿真结果表明:不进行修正的初始定距结果R1的误差在±1.5 m的范围内,在利用了高频差定距结果后,其一次距离修正后误差在±0.5 m的范围内,二次修正和三次修正后定距误差能控制在0.2 m的范围内。距离修正模块在有效解决距离模糊的前提下,极大提高了定距精度。
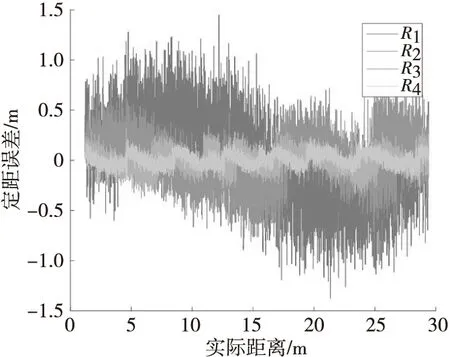
图6 距离修正模块各级修正误差图Fig.6 Ranging error chart of each level distance correction module
为检验该算法抗噪声性能,对不同信噪比条件下的系统定距精度进行了仿真,其结果如图7所示。在SNR=15 dB时,定距误差在0.2 m的范围内,当SNR=0 dB的情况下误差能控制在2 m的范围内。即使在信噪比为-5 dB的情况下,系统定距误差也能保持4 m范围以内。
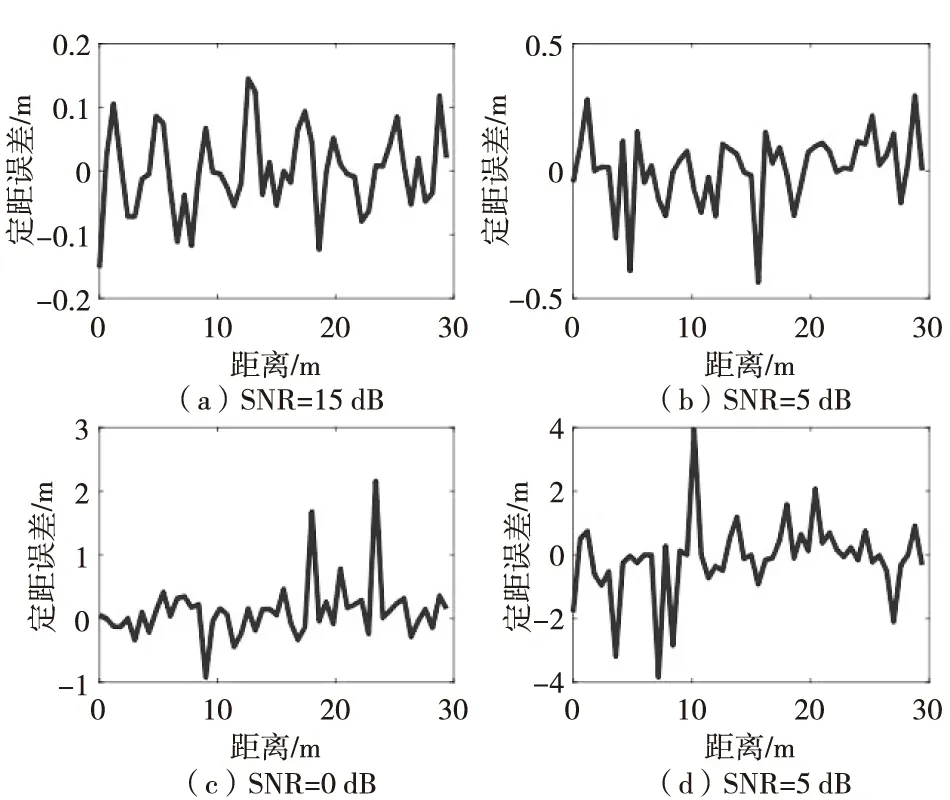
图7 不同信噪比下算法定距误差Fig.7 The ranging error of the algorithm under different SNR
3 算法板级测试
算法测试实验通过单端口ROM模拟了产生不同距离下的回波信号,利用Quartus软件的在线调试工具SignalTap读取FPGA内部数字信号处理状态,通过JTAG接口对5 m时的回波信号、各个子载波和定距结果进行了实时采样,采样结果如图8所示。
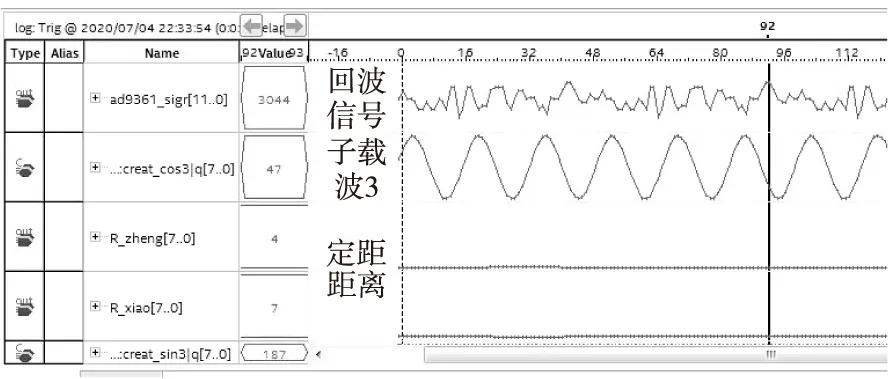
图8 信号处理过程实时采样结果图Fig.8 Real-time sampling results of signal processing
在信噪比为15 dB时,经输入不同距离回波信号的多载波相位定距算法定距结果如表1所示。系统在多个距离下的定距误差均保持在在0.5 m的范围内,相比Matlab仿真硬件电路信号处理具有较少的数据位数,因此其定距误差相对较大,但该系统的定距精度仍远大于传统相位定距单个载波的定距精度。
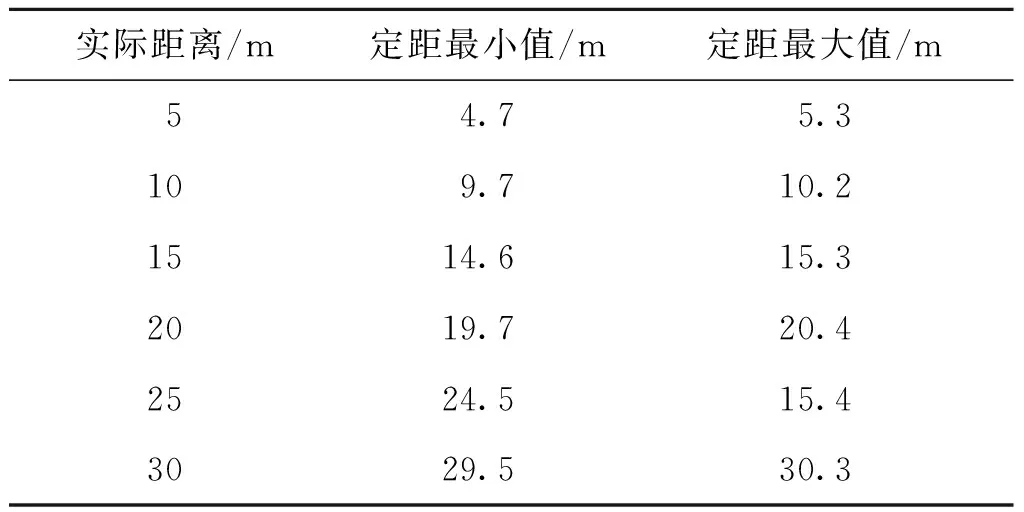
表1 不同距离下算法的测试结果Tab.1 Test results of the algorithm at different distances
当调制频偏为20 MHz时,系统采用调频定距算法在此软件无线电的固定误差为3.75 m,多载波相位定距算法定距误差明显小于调频定距算法。板级测试验证了算法在软件无线电平台上的可行性,同时有效提高了系统的定距精度,改善了系统的性能。
4 结论
本文提出了基于OFDM的多载波相位定距算法,算法通过多次距离修正利用多个频率的定距值有效解决了相位定距过程中定距精度和最大不模糊距离之间的矛盾。Matlab仿真证明了算法具有出色的抗噪声性能,算法板级测试表明系统定距误差在0.5 m的范围内,具有较高的定距精度,有效提高了软件无线电引信系统的定距性能。
