环状刻槽钻铤中随钻方位电磁波响应的混合算法
2021-05-07汪宏年于蕾王浩森杨守文殷长春
汪宏年 , 于蕾, 王浩森, 杨守文, 殷长春
1 吉林大学计算方法与软件国际中心, 长春 130012 2 河北建筑工程学院, 河北 张家口 075000 3 吉林大学地球探测科学与技术学院, 长春 130026
0 引言
随钻电磁波测井技术已成为地质导向和地层评价的重要工具,用于实时确定钻铤周围的地层电导率、地层界面或油水接触面的位置,实现井眼轨迹优化.常规随钻电磁波仪器通常由两对不同源距的共轴发射线圈与一对共轴接收线圈组成,进行补偿式测量,提供长短源距与不同频率的共轴电磁响应(Clark et al., 1990).这种单一共轴电磁响应不仅难以准确地提供地层电导率以及各向异性信息,也无法直接确定层界面两边电导率的相对大小与变化情况,从而给复杂地层条件下(断块、裂缝地层、起伏地形等)地质导向造成困难(Omeragic et al., 2005).因此,多分量随钻电磁波测井技术已经成为当前主要的研究发展方向(Bell et al., 2006;Fang, 2011).此外,需要指出的是,随钻电磁波测井仪器的探头安装在钻头附近,对传感器的抗震性有非常高的要求.因此,实际随钻测井仪器中所有发射与接收线圈均安装在钻铤表面的环状刻槽中,槽中充填着铁氧体等磁性材料来提高线圈的发射和接收效率,同时在铁氧体外部再充填一层玻璃钢等高阻耐磨材料(Shumpert and Butler, 1998;Park and Eom, 1999;Wang et al., 2007).由于真实随钻电磁测井仪器的钻铤表面不再光滑且发射与接收线圈均镶嵌在环状刻槽中,使得其电磁响应的数值模拟变得更加复杂,但目前与其相关的完整数值模拟方法与数值结果的报道非常少.
目前,应用于随钻电磁波测井的正演模拟方法主要包括:忽略钻铤与井眼影响的解析法 (Wang et al., 2008;姚东华等, 2010;汪建勋等, 2013;Yang et al., 2014;王磊等, 2018, 2020;康庄庄等, 2020),2维和2.5维模式匹配算法(Tamarchenko and Druskin, 1993;Wang and Yang, 2001; Wang et al., 2012;谭茂金等, 2007;邢光龙等, 2008;朱天竹等, 2017;林蔺等, 2017),3维有限差分法(Wang and Signorelli, 2004;Lee et al., 2012;Zeng et al., 2018)、3维有限体积法 (张烨等, 2012;王浩森等, 2016;Wang et al., 2020)以及3维有限元法(Pardo et al., 2006;俞燕明等, 2013).忽略钻铤与井眼效应的解析算法由于计算速度快且计算结果能够清楚地反映出井眼周围地层电导率的变化情况,往往被应用于随钻电磁波测井探边能力考察(Li et al., 2018)以及视电导率提取等(白彦等, 2018);2维模式匹配算法由于其计算速度快且计算精度高,在侧向测井和感应测井正反演中得到了广泛应用.这些2维或3维正演模拟算法往往用光滑圆柱形导体来代替光滑钻铤,并假设发射与接收线圈缠绕在光滑钻铤的外表面,使数值模拟过程大大简化(王浩森等, 2016;Wang et al., 2020).然而,实际钻铤表面包含着多个环状刻槽且充填着高磁导率的铁氧体和高阻玻璃钢外罩,各个线圈安装在环状刻槽内部(Park and Eom, 1999;Wang and Signorelli, 2004;于蕾等, 2020).由于环状刻槽以及槽中的充填物对随钻电磁测井响应存在影响,建立含有刻槽钻铤的随钻电磁测井响应正演模拟方法,并研究考察其相关的仪器响应有十分重要的意义.
本文将针对中国科学院地质与地球物理研究所自主研发的随钻方位电磁波测井仪器(LWD Azimuthal Electromagnetic Tool, LWD-AEMT),利用混合算法研究建立一套完整的数值模拟方法.首先根据环状刻槽的位置,将整个非光滑钻铤划分成多个具有不同层厚、不同电导率和磁导率分布的轴对称非均质层状模型,进而应用混合法给出每个层状非均质地层中电场和磁场的半解析解.然后,选取多个不同磁导率的铁氧体和不同电导率的地层,系统地分析发射线圈的自感电动势和接收线圈上感应电动势的变化特征,考察发射线圈的发射功率以及阻抗随铁氧体磁导率和地层电导率的变化关系,以便为仪器设计过程中铁氧体磁导率的选取提供理论依据.同时,通过计算各接收线圈上感应电动势的大小,定量地给出各个接收器上接收信号的动态范围.最后,利用摄动理论建立各个接收器上感应电动势的微小变化与地层电导率的微小变化之间的关系,给出随钻电磁波测井空间灵敏度的计算方法,并通过数值模拟结果分析不同源距的振幅比与相位差空间灵敏度的变化特征.
1 理论
1.1 随钻方位电磁波测井仪器结构与测量原理
图1a是随钻方位电磁波传感器结构示意图.整个传感器由一对长源距共轴发射线圈Tz1/Tz2、一对短源距共轴发射线圈Tz3/Tz4、一对共轴接收线圈Rz1/Rz2与一对共面接收线圈Rx1/Rx2组成(Fang, 2011;刘乃震等, 2015;Wang et al., 2020).每对线圈均对称地分布在仪器中心位置的两边,能够提供补偿测量,降低层边界的影响.为便于进行数值模拟,长、短源距发射线圈到仪器中心的距离分别用LTz12和LTz34表示,共轴接收线圈和共面接收线圈到仪器中心的距离分别为LRz12和LRx12.钻铤外半径bmandrel、环状刻槽径向深度dgroov、纵向长度Lgroov以及环状刻糟部分的钻铤内半径bgroov=bmandrel-dgroov等参数见表1.钻铤电导率σmandrel、铁氧体电导率σferrite和相对磁导率μr,ferrite以及玻璃钢电导率σglass和相对磁导率μr,glass等相关参数见表2,其中铁氧体的相对磁导率μr,ferrite可以取不同的值.所有共轴线圈均缠绕在铁氧体与玻璃钢之间,位于环状刻槽的中心位置,半径为ρT=ρR=bmandrel-dgroov/2.与共轴接收线圈不同,共面接收线圈的法线方向垂直于钻铤表面,贴附在铁氧体与玻璃钢之间,由两个大小、形状相同的柱面线圈组成且对称地安装在刻槽钻铤轴线两侧,到井轴距离为ρR,法方向对应的方位角分别为φR和π+φR.此外,井眼半径为a、泥浆电导率为σmd.为简单起见,假定钻铤居于井眼中心,井眼外地层电导率σ是均匀的.为了能够利用混合法对随钻方位电磁波测井响应进行数值模拟,在每个环状刻槽的上下边界添加水平虚拟层边界,使其成为一个水平层状模型,dn(n=1,2,…,N+1)为虚拟层边界的位置,且d1=-∞,dN+1=+∞,N=17是总层数(见图1b).

表1 刻槽钻铤和环状刻槽的尺寸Table 1 Dimensions of grooved mandrel and annular grooves
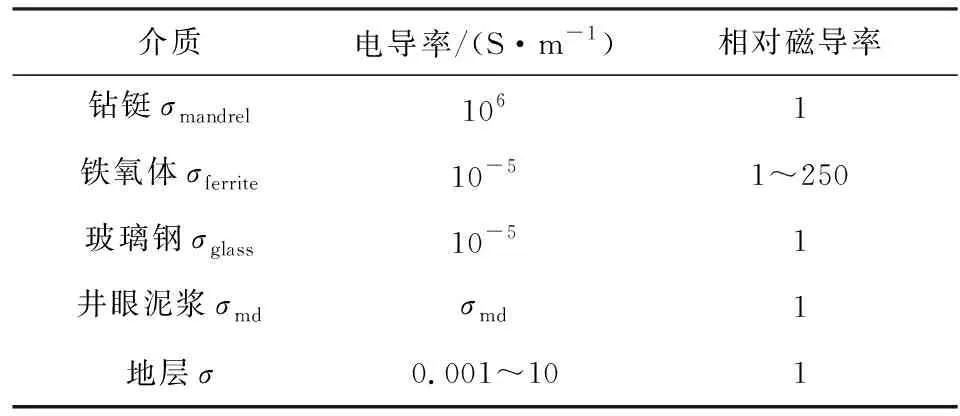
表2 介质的电导率和相对磁导率Table 2 Conductivity and relative permeability of mediums
由于金属钻铤、井眼以及地层电导率的空间分布是柱对称的,并且仅存在共轴发射线圈,因此,各个线圈产生的电磁场可通过混合法加以求解.为方便起见,我们将环状刻槽所在层的电导率和相对磁导率的径向分布分别表示为
(1)
和
(2)
而不含环状刻槽的层的相对磁导率等于1,其电导率的径向分布可表示为
(3)
1.2 随钻方位电磁波测井响应混合算法
对于图1b的层状非均质模型,位于zT处、半径为ρT的共轴发射线圈产生的电磁场满足如下Maxwell方程 (时间因子为e-iω t):
(4)
其中,σ*(r)=-iωε(r)+σ(r)为空间复电导率;为简单起见,介电常数等于真空中的介电常数,即ε(r)=ε0;I为发射电流振幅.
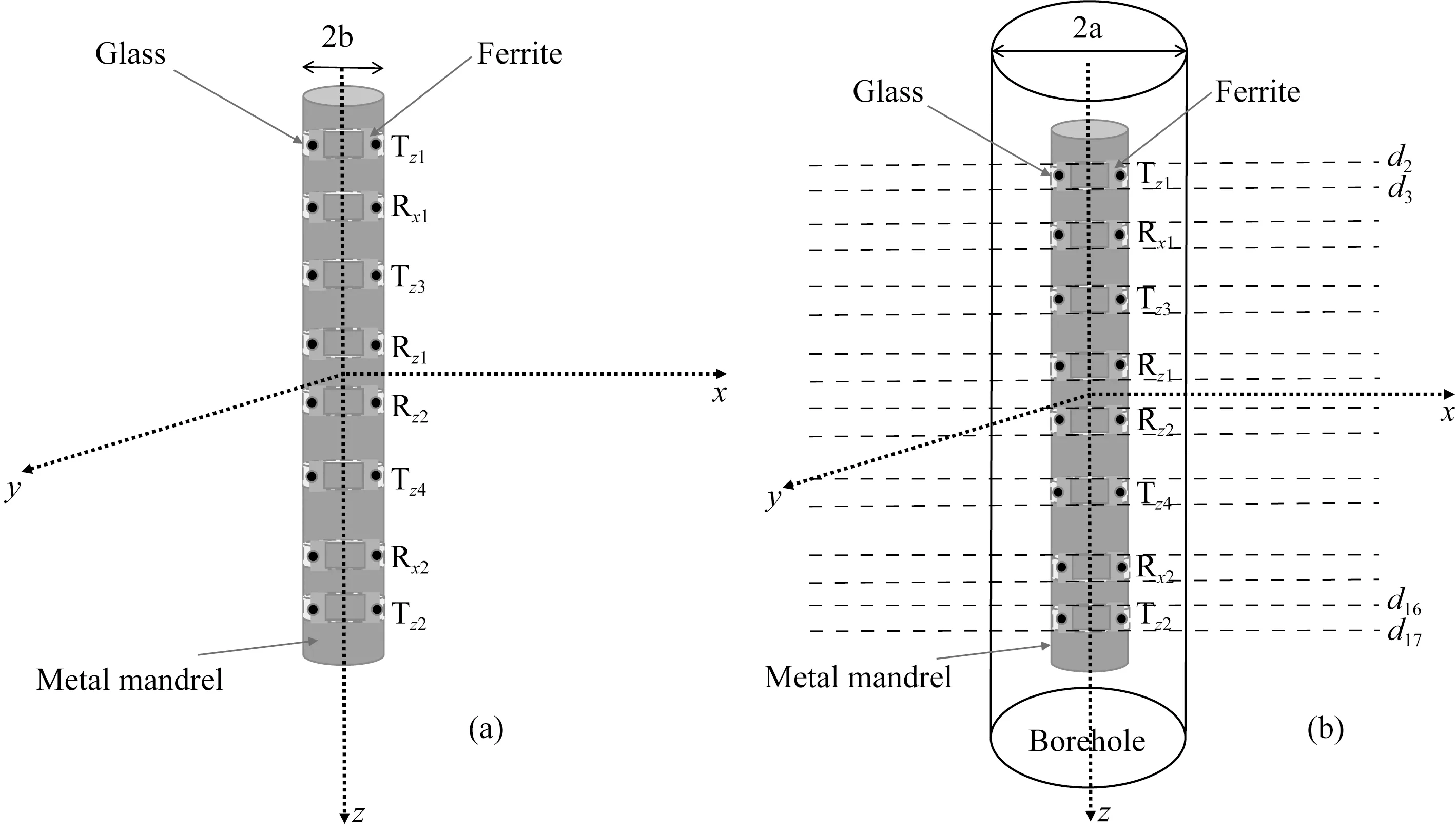
图1 随钻方位电磁波测井井下环状刻槽钻铤上传感器结构示意图(a) 环状刻槽钻铤上发射和接收线圈系; (b) 用于数值模拟的层状地层模型.Fig.1 The downhole sensor of the LWD-AEMT mounted on annular grooved mandrel(a) Transmitting and receiving coils on annular grooved mandrel; (b) Horizontal layered model for numerical simulation.
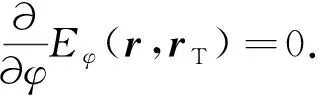
=iωμ0Iδ(ρ-ρT)δ(z-zT),ρ>bgroov,
(5)
其中,
(6)
为二阶微分算子(Wang and Yang, 2001; Wang et al., 2012).且Eφ分量在各个水平界面上满足如下条件:
(7a)
而在环状刻槽表面对应的柱状界面ρ=bgroov上,满足齐次边界条件:
Eφ(ρ,z;ρT,zT)|ρ=bgroov=0.
(7b)
为获得方程(5)在边界条件(7)下的解,假定接收点位于第n层地层且位置为(ξ,η),引入方程(5)在第n层地层中的对偶函数gn(ρ,z;ξ,η)(Tamarchenko and Druskin, 1993;Wang and Yang, 2001):
δ(ρ-ξ)δ(z-η),ρ>bgroov,
(8)
其中,
(9)
则利用混合法可得到方程(8)的半解析解(见附录A):
(10)
其中,ST(ρ)=(φ1(ρ),φ2(ρ),…,φ2k(ρ),…,φ2K(ρ))是在足够长的径向区间[bgroov,ρMX]内的不均匀离散节点ρk(k=0,1,2,…,2K+1)上的插值基函数组成的行向量(Wang and Yang, 2001; Wang et al., 2012).选用如下Newton基函数,即在偶数节点上:
k=1,2,…,K
(11)
而在奇数节点上:
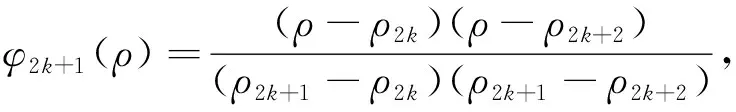
ρ2k≤ρ≤ρ2k+2,
k=0,1,…,K
(12)
并且假定径向最小节点和最大节点分别为ρ0=bgroov和ρ2K+1=ρMX,通常选取ρMX=30m.
利用Green第二积分公式将方程(5)和(8)结合,可以得到空间电场的积分解:
(13)
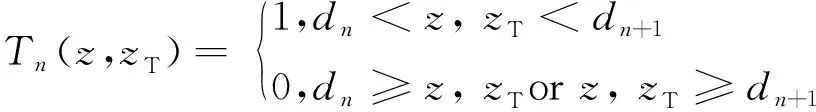
为快速计算各个水平界面上的电场,将水平边界上各个径向离散节点ρk(k=1,2,…,2K)上的电场组合成2K阶列向量的形式:
(14)
同时,结合方程(11)和(12),每个水平界面上的电场可以表示成如下紧凑形式:
(15)
将方程(10)和(15)代入到 (13)中,得到如下矩阵形式的空间电场:
Eφ,n(ρ,z;ρT,zT)=
(16)
此外,为了确定各个水平界面上的电场,将边界条件(7a)和方程(16)结合,得到关于未知向量Un(ρT,zT)的代数方程:
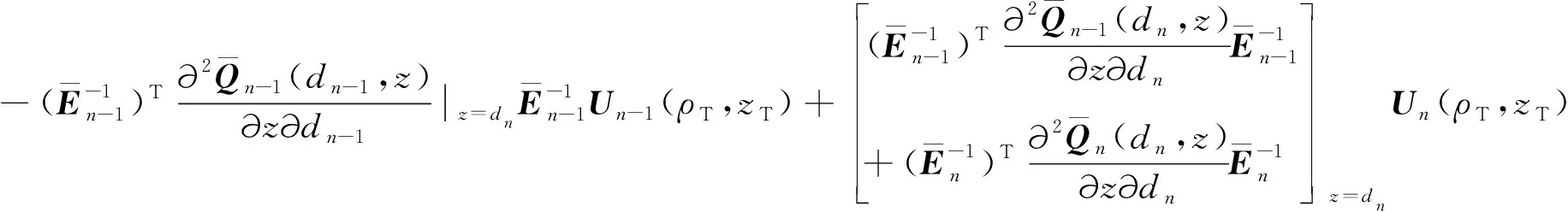
(17)
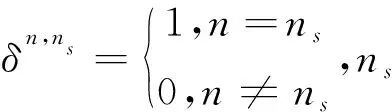
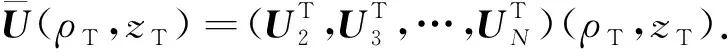
H(ρ,z;ρT,zT)=
(18)
1.3 随钻方位电磁波测井响应的空间灵敏度
当电导率存在微小摄动时,zT处共轴发射线圈在zR处接收器上的感应电动势V(zR;zT)=2πρREφ(ρR,zR;ρT,zT)会产生相应的变化δV(zR;zT).利用摄动原理与Green积分公式,可以得到感应电动势微小变化δV(zR;zT)与电导率摄动量δσ(ρ,z)间的关系为(Wang et al., 2012):
×σ-1(ρ,z)δσ(ρ,z)dρ,
(19)
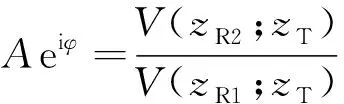
(20)
将(19)代入(20)中,并整理可得:
(21)
其中,
(22)
分别是电场振幅比与相位差的空间灵敏度函数.其物理含义是半径为ρ、厚度为dρ和高度为dz的小圆环上,当电导率的相对变化量为σ-1(ρ,z)δσ(ρ,z)时,振幅与相位的相对微小变化.
2 数值结果
本节将通过数值模拟结果研究考察铁氧体的相对磁导率变化对随钻方位电磁测井响应的影响,以便为铁氧体磁导率的选择提供理论依据.在此基础上,通过对刻槽钻铤、光滑钻铤与无钻铤情况的测井响应进行对比分析,研究分析刻槽钻铤对随钻方位电磁波测井响应的影响.
2.1 算法验证
首先将前面的混合法(Hybrid method)与三维有限体积法(3D FVM)的数值结果进行对比,以验证混合法的有效性.为简单起见,假定钻铤中铁氧体充填物的相对磁导率为150,并选取29个不同的地层电导率:0.001、0.01、0.02、0.05、0.06、0.07、0.085、0.1、0.125、0.2、0.275、0.35、0.4、0.5、0.6、0.7、0.8、0.9、1.0、1.25、2.0、2.75、3.50、4.0、5.0、6.0、7.0、8.0和10.0 S·m-1.图2是400 kHz和2 MHz两个工作频率情况下,分别由本文的混合法与三维有限体积法(于蕾等, 2020)得到的共轴电磁响应对比图.其中,图2a和2c分别是长短源距振幅比响应,图2b和2d分别是长短源距相位差响应.由图可以看出,无论是振幅比还是相位差,两种方法的计算结果几乎完全重合,其相对误差小于1%.
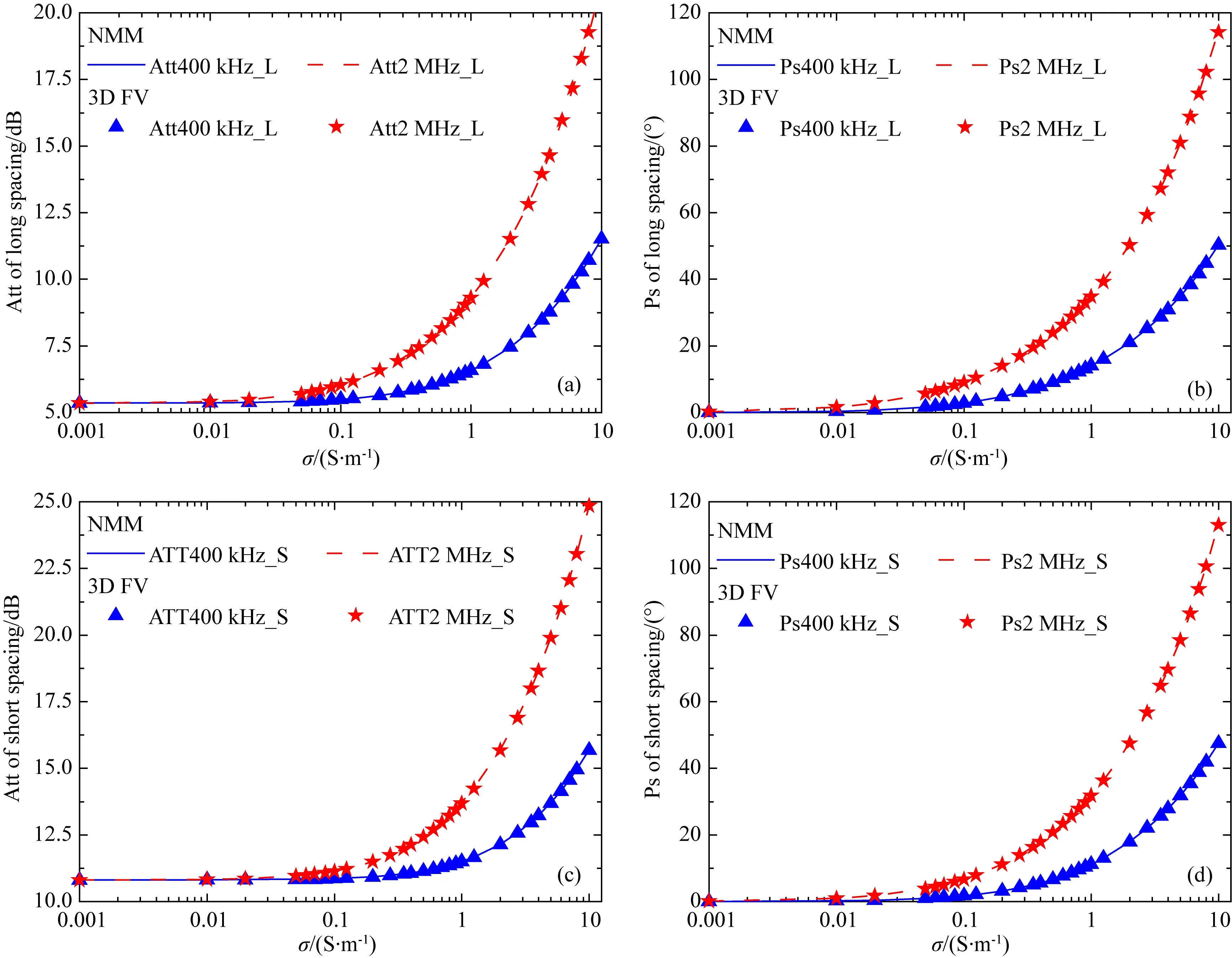
图2 均匀各向同性地层中由混合法与三维有限体积法得到的随钻共轴电磁响应对比(a) 长源距振幅比; (b) 长源距相位差; (c) 短源距振幅比; (d) 短源距相位差. 蓝色实线和红色虚线是混合法数值结果,蓝色▲和红色★离散符号是三维有限体积法数值结果.Fig.2 Comparison of LWD coaxial EM responses computed by Hybrid method with that by 3D FV method in homogenous formation with the conductivity ranging from 0.001 to 10S/m(a) Attenuation of long spacing; (b) Phase shift of long spacing; (c) Attenuation of short spacing; (d) Phase shift of short spacing.
2.2 刻槽钻铤、光滑钻铤与无钻铤随钻电磁波测井响应的对比
采用与图2相同的地层模型,分别利用混合法(Hybrid method)和传输线法(TLM)计算出光滑钻铤和无钻铤情况下的随钻电磁波测井响应,并与图2中刻槽钻铤情况下的共轴电磁响应进行对比,考察刻槽钻铤、光滑钻铤和无钻铤三种不同情况下随钻电磁波测井响应的差异.对于光滑钻铤情况,假定所有发射与接收线圈均安装在柱状钻铤外、距离钻铤表面0.005 m处;而无钻铤情况则将发射与接收线圈看作磁偶极子.图3同时给出了三种不同情况下高频与低频共轴响应的数值模拟结果.其中,图3a和3c分别是长短源距振幅比,而图3b和3d是长短源距相位差.从图3a和图3c的数值结果不难看出,无钻铤情况的振幅比与刻槽钻铤和光滑钻铤情况的振幅比相差很大,特别是短源距振幅比的最大差值超过了50%.因此,利用不考虑钻铤影响的仪器模型研究随钻方位电磁波测井响应会产生很大的误差.然而,与振幅比的响应特征不同,图3b和图3d的数值结果显示刻槽钻铤、光滑钻铤与无钻铤三种情况下计算得到的相位差差异较小,即相位差响应受钻铤和刻槽的环状影响非常小.
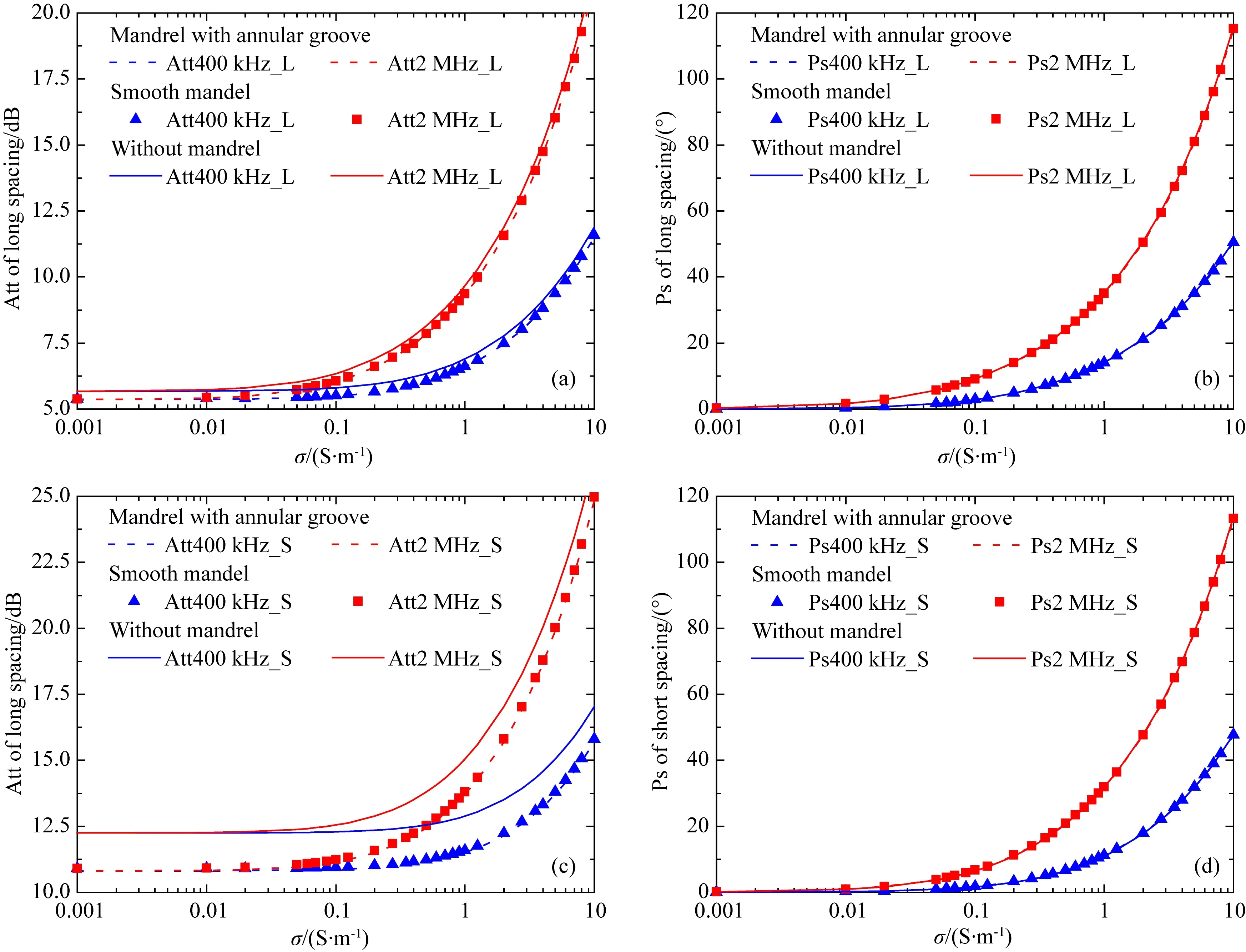
图3 均匀各向同性地层中刻槽钻铤、光滑钻铤与无钻铤情况下随钻共轴电磁响应对比(a) 长源距振幅比; (b) 长源距相位差; (c) 短源距振幅比; (d) 短源距相位差. 蓝色与红色虚线以及离散符号▲和■分别是刻槽钻铤与光滑钻铤的测井响应(混合法求得),蓝色与红色实线是无钻铤情况下的测井响应(由传输线法得到).Fig.3 Comparison of LWD coaxial EM responses for three different mandrels: with annular groove, smooth mandrel and without mandrel in homogenous formation(a) Attenuation of long spacing; (b) Phase shift of long spacing; (c) Attenuation of short spacing; (d) Phase shift of short spacing.
2.3 铁氧体磁导率对随钻方位电磁波测井仪器的发射功率和接收线圈上感应电动势的影响
由于随钻方位电磁波测井仪器主要采用蓄电池或泥浆发电机供电,在仪器设计中需要了解仪器功耗、发射线圈阻抗、接收线圈信号动态范围等信息,以便合理分配有限的电力资源.为此,我们选择22个不同的地层电导率σ:0.001、0.01、0.02、0.05、0.08、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0、1.5、2.0、3.0、4.0、5.0、8.0和10.0 S/m,以及22个不同的铁氧体相对磁导率μr:1、1.3、1.7、2.2、2.8、3.7、4.8、6.3、8.1、10.6、13.7、17.9、23.3、30.3、39.4、51.2、66.5、86.5、112.5、146.2、190和240,利用混合法计算四个发射线圈(Tz1、Tz2、 Tz3和Tz4)上的自感电动势以及两个共轴接收线圈(Rz1和Rz2)和单边共面接收线圈(Rx1和Rx2)上的感应电动势,进而利用计算结果研究分析不同地层电导率和不同铁氧体磁导率情况下仪器发射功率、发射阻抗以及接收线圈上感应电动势的动态变化范围,为选择合适的铁氧体磁导率提供理论依据.
2.3.1 仪器发射功率与发射阻抗的变化特征
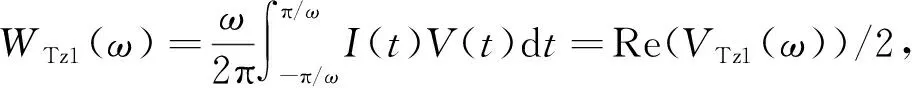
图4是工作频率为400 kHz和2 MHz情况下发射线圈Tz1上的自感电动势的正演模拟结果.其中,图4a和图4b是400 kHz情况下自感电动势的实部和虚部,而图4c和图4d是2 MHz情况下自感电动势的实部和虚部.由于自感电动势的虚部大小主要反映线圈的直耦电动势,其受地层电导率的影响较小,但受铁氧体磁导率变化的影响却非常大(见图4b和4d),且随着铁氧体磁导率的增加而单调变化.而自感电动势的实部对地层电导率和铁氧体磁导率变化均较为敏感(见图4a和图4c).此外,在μr<20的范围内,自感电动势的实部(即波阻抗值与发射功率)受铁氧体磁导率的影响最明显,随后铁氧体磁导率的增加对波阻抗值与发射功率的影响逐渐减弱,且当μr增加到150后,波阻抗值与发射功率似乎进入饱和状态.由此不难推断:选择μr=200的铁氧体磁导率作为环状刻槽的充填物较为合适.此外,当μr=200固定不变时,由图4a和4c的数值结果可以看出,在整个电导率变化范围内,低频和高频发射功率大约为2.3 W和6 W,相差2倍以上,而波阻抗大约为4.6+620i和12+3100i.
图4 发射线圈Tz1上的自感电动势随地层电导率和铁氧体磁导率的变化关系(a) 低频、实部; (b) 低频、虚部; (c) 高频、实部; (d) 高频、虚部.Fig.4 Self-induced voltage on the transmitting antenna Tz1 for different formation conductivity and ferrite relative permeability(a) Real part for 400 kHz; (b) Imaginary part for 400 kHz; (c) Real part for 2 MHz; (d) Imaginary part for 2 MHz.
2.3.2 共轴接收线圈上的感应电动势以及振幅比和相位差的变化特征
为考察地层电导率和铁氧体磁导率变化对共轴接收线圈上的感应电动势的影响及其动态变化范围,图5和图6分别给出400 kHz和2 MHz工作频率下长源距发射线圈Tz1在共轴接收线圈Rz1和Rz2上对应的感应电动势Vz1和Vz2.结果显示:感应电动势的实部和虚部对地层电导率和铁氧体相对磁导率的变化均较为敏感,且几乎是相对磁导率的单调增函数;与发射线圈上自感电动势的特征不同,地层电导率变化对两个接收线圈上感应电动势的影响更为明显.根据图5和图6的计算结果可以清楚地看到不同地层电导率和铁氧体相对磁导率情况下两个共轴接收线圈上感应电动势的动态变化范围,为接收电路设计提供重要参数.
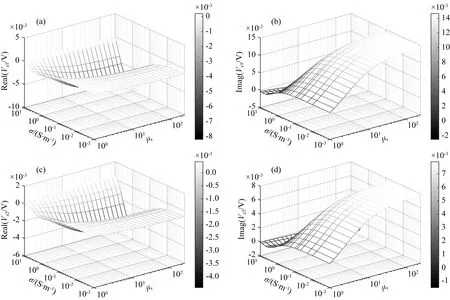
图5 发射线圈Tz1在共轴接收线圈Rz1和Rz2上的感应电动势(Vz1和Vz2)随地层电导率和铁氧体相对磁导率的变化关系(400 kHz)(a) Vz1实部; (b) Vz1虚部; (c) Vz2实部; (d) Vz2虚部.Fig.5 The induced voltage (Vz1 and Vz2) of transmitter coil Tz1 on coaxial receiving coils Rz1 and Rz2 for different formation conductivity and ferrite relative permeability (400 kHz)(a) Real part of Vz1; (b) Imaginary part of Vz1; (c) Real part of Vz2; (d) Imaginary part of Vz2.
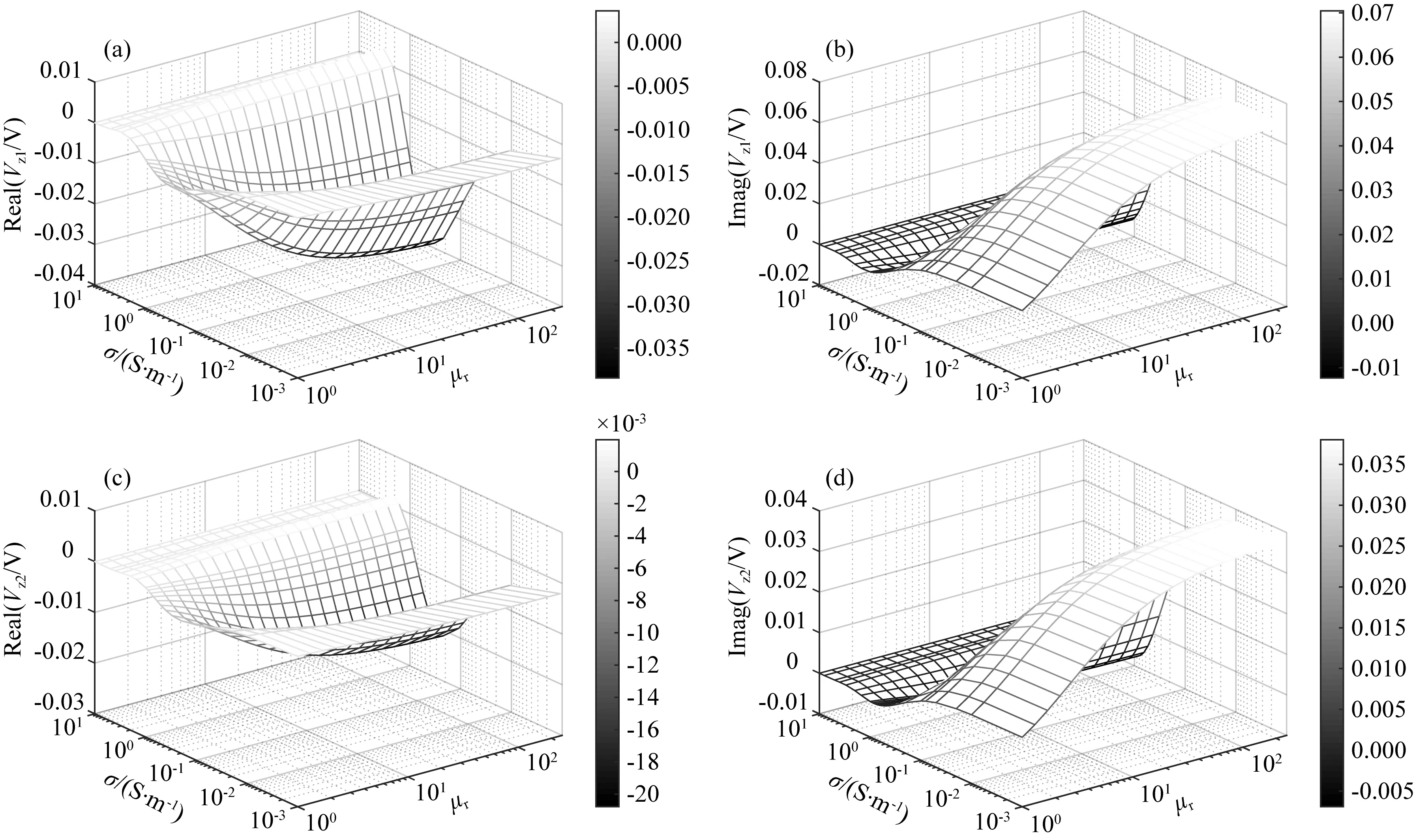
图6 发射线圈Tz1在共轴接收线圈Rz1和Rz2上的感应电动势(Vz1和Vz2)随地层电导率和铁氧体相对磁导率的变化关系(2 MHz)(a) Vz1实部; (b) Vz1虚部; (c) Vz2实部; (d) Vz2虚部.Fig.6 The induced voltage (Vz1 and Vz2) of transmitter coil Tz1 on coaxial receiving coils Rz1 and Rz2 for different formation conductivity and ferrite relative permeability (2 MHz)(a) Real part of Vz1; (b) Imaginary part of Vz1; (c) Real part of Vz2; (d) Imaginary part of Vz2.
由于随钻方位电磁波测井的输出资料是轴向感应电动势的振幅比和相位差,为此,图7和图8分别给出了400 kHz和2 MHz工作频率下,长短源距发射线圈在共轴接收线圈Rz1和Rz2上感应电动势的振幅比(Att)与相位差(Ps).从图可以看出,振幅比与相位差几乎不受环状刻槽中磁导率的影响,产生这一现象的原因是环状刻槽中铁氧体的体积相对较小,仅仅影响了其周围较小范围内的电磁场空间分布,而对远离铁氧体的钻铤外部地层中的电磁场影响非常小.这也说明充填的铁氧体有效地提高了发射线圈的发射功率、增加了波阻抗、同时也提高了接收线圈上感应电动势的强度,但对钻铤外的电磁场空间分布影响不明显,因此,共轴接收线圈上感应电动势的振幅比(Att)与相位差(Ps)主要反映地层电导率的变化特征.

图7 共轴接收线圈Rz1和Rz2上感应电动势的振幅比(Att)与相位差(Ps)随地层电导率和铁氧体相对磁导率的变化关系(400 kHz)(a) 长源距振幅比; (b) 长源距相位差; (c) 短源距振幅比; (d) 短源距相位差.Fig.7 Attenuation and Phase shift of induced voltage on coaxial receiving coils Rz1 and Rz2 for different formation conductivity and ferrite relative permeability (400 kHz)(a) Attenuation of long spacing; (b) Phase shift of long spacing; (c) Attenuation of short spacing; (d) Phase shift of short spacing.

图8 共轴接收线圈Rz1和Rz2上感应电动势的振幅比(Att)与相位差(Ps)随地层电导率和铁氧体相对磁导率的变化关系(2 MHz)(a) 长源距振幅比; (b) 长源距相位差; (c) 短源距振幅比; (d) 短源距相位差.Fig.8 Attenuation and Phase shift of induced voltage on coaxial receiving coils Rz1 and Rz2 for different formation conductivity and ferrite relative permeability (2 MHz)(a) Attenuation of long spacing; (b) Phase shift of long spacing; (c) Attenuation of short spacing; (d) Phase shift of short spacing.
2.3.3 共面接收线圈上感应电动势的变化特征
与常规随钻电磁波仪器相比,随钻方位电磁波仪器在钻铤上增加了两个共面接收线圈Rx1和Rx2,用于测量电磁场横向分量,提高探边能力和各向异性识别能力.由于每个共面接收线圈有两个大小相同的小线圈对称地贴附在钻铤两边(Wang et al., 2020),其角度正好相差180°,在直井情况下,对于单个的小线圈,由于其不在钻铤的轴线上,感应电动势不等于零,且对称分布的两个小线圈上的感应电动势大小相同、符号相反,因此,直井中Rx1和Rx2上的感应电动势等于零.所以,这里我们考察共面接收线圈中单个小线圈上的感应电动势随地层电导率和铁氧体相对磁导率的变化情况.图9和图10分别是400 kHz和2 MHz工作频率下,在不同地层电导率和铁氧体相对磁导率的情况下由发射线圈Tz2和Tz4在共面接收线圈Rx1的单边小线圈上产生的感应电动势.结果显示:地层电导率和铁氧体相对磁导率变化对横向感应电动势影响非常大.图11给出了不同地层电导率和铁氧体相对磁导率情况下共面接收线圈Rx1的单边小线圈上的合成感应电动势Vzx1(刘乃震等, 2015;Wang et al., 2020),合成后的横向感应电动势受铁氧体磁导率的影响仍然很大.从数值结果不难推断,由于横向感应电动势本身很小,加入高磁导率的铁氧体后可以大大增加横向感应电动势的强度,有利于提高横向分量的测量精度.
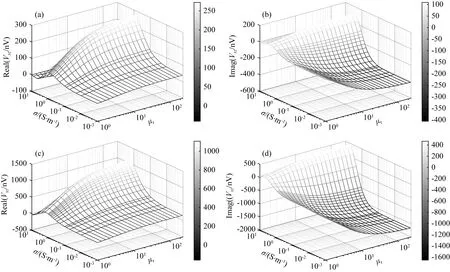
图9 发射线圈Tz2和Tz4在共面接收线圈Rx1的单边小线圈上产生的感应电动势Vxz随地层电导率和铁氧体相对磁导率的变化关系(400 kHz)(a) Tz2产生的Vxz实部; (b) Tz2产生的Vxz虚部; (c) Tz4产生的Vxz实部; (d) Tz4产生的Vxz虚部.Fig.9 The induced voltage Vxz on the single-side coil of the coplanar coil Rx1 by the transmitter coils Tz2 and Tz4 for different formation conductivity and ferrite relative permeability (400 kHz)(a) Real part of Vxz by Tz2; (b) Imaginary part of Vxz by Tz2; (c) Real part of Vxz by Tz4; (d) Imaginary part of Vxz by Tz4.
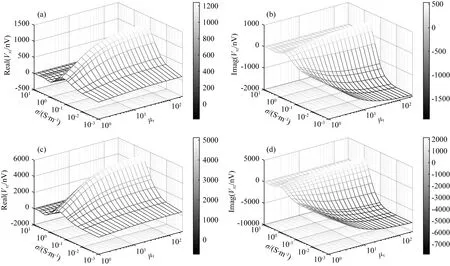
图10 发射线圈Tz2和Tz4在共面接收线圈Rx1的单边小线圈上产生的感应电动势Vxz随地层电导率和铁氧体相对磁导率的变化关系(2 MHz)(a) Tz2产生的Vxz实部; (b) Tz2产生的Vxz虚部; (c) Tz4产生的Vxz实部; (d) Tz4产生的Vxz虚部.Fig.10 The induced voltage Vxz on the single-side coil of the coplanar coil Rx1 by the transmitter coils Tz2 and Tz4 for different formation conductivity and ferrite relative permeability (2 MHz)(a) Real part of Vxz by Tz2; (b) Imaginary part of Vxz by Tz2; (c) Real part of Vxz by Tz4; (d) Imaginary part of Vxz by Tz4.
2.3.4 共轴接收线圈上的直耦电动势及其对仪器响应的影响
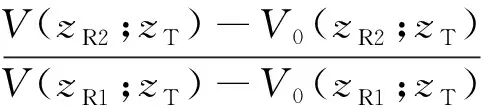
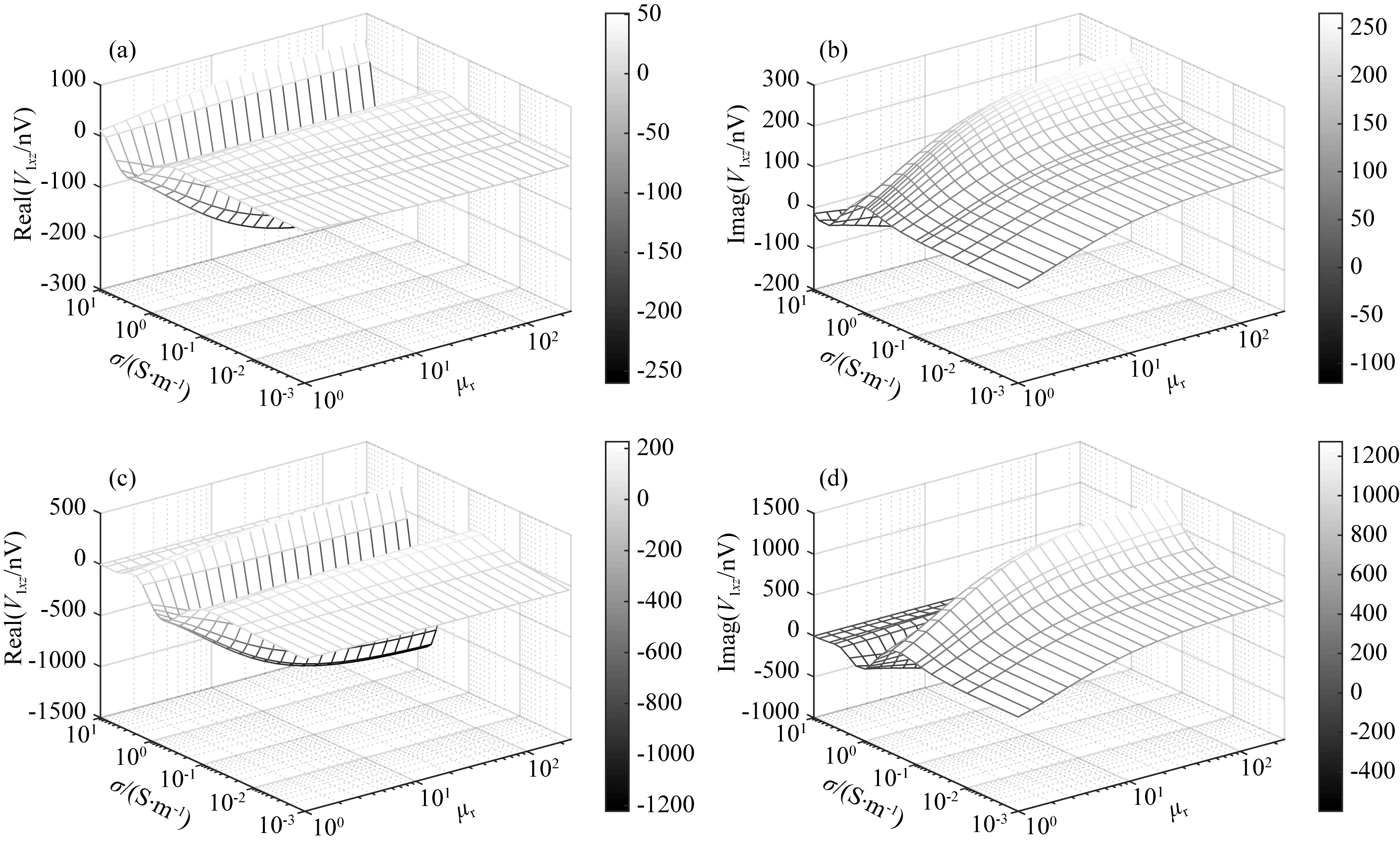
图11 共面接收线圈Rx1的单边小线圈上的合成感应电动势V1xz随地层电导率和铁氧体相对磁导率的变化关系(a) 低频、实部; (b) 低频、虚部; (c) 高频、实部; (d) 高频、虚部.Fig.11 The synthetic induced voltage V1xz on the single-side coil of the coplanar coil Rx1 by both transmitter coils Tz2 and Tz4 for different formation conductivity and ferrite relative permeability(a) Real part for 400 kHz; (b) Imaginary part for 400 kHz; (c) Real part for 2 MHz; (d) Imaginary part for 2 MHz.
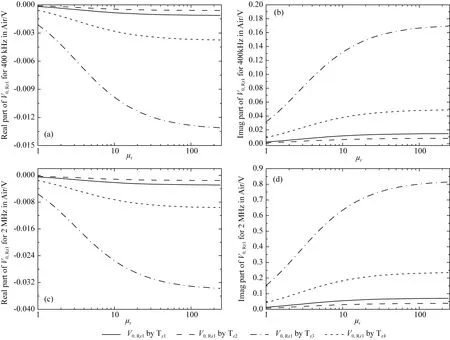
图12 四个发射线圈分别在共轴接收线圈Rz1上的直耦电动势随铁氧体磁导率的变化关系(a) 低频、实部; (b) 低频、虚部; (c) 高频、实部; (d) 高频、虚部.Fig.12 Direct coupling voltage on the coaxial receiver Rz1 by the four transmitters in air for different ferrite relative permeability(a) Real part for 400 kHz; (b) Imaginary part for 400 kHz; (c) Real part for 2 MHz; (d) Imaginary part for 2 MHz.

图13 消除直耦信号影响后的共轴接收线圈上感应电动势的振幅比和相位差随地层电导率和铁氧体相对磁导率的变化关系(400 kHz)(a) 长源距振幅比; (b) 长源距相位差; (c) 短源距振幅比; (d) 短源距相位差.Fig.13 Attenuation and Phase shift of induced voltage on coaxial receivers for different formation conductivity and ferrite relative permeability after removing direct coupling signal (400 kHz)(a) Attenuation of long spacing; (b) Phase shift of long spacing; (c) Attenuation of short spacing; (d) Phase shift of short spacing.

图14 消除直耦信号影响后的共轴接收线圈上感应电动势的振幅比和相位差随地层电导率和铁氧体相对磁导率的变化关系(2 MHz)(a) 长源距振幅比; (b) 长源距相位差; (c) 短源距振幅比; (d) 短源距相位差.Fig.14 Attenuation and phase shift of induced voltage on coaxial receivers for different formation conductivity and ferrite relative permeability after removing direct coupling signal (2 MHz)(a) Attenuation of long spacing; (b) Phase shift of long spacing; (c) Attenuation of short spacing; (d) Phase shift of short spacing.
2.4 空间灵敏度
利用空间灵敏度计算公式(22),可以确定随钻方位电磁波测井共轴响应的振幅比与相位差的空间灵敏度分布.图15和图16是在地层电导率为0.1 S·m-1的情况下,2 MHz工作频率时短源距与长源距的振幅比与相位差空间灵敏度分布情况.首先,从图中可以看出,钻铤中的环状刻槽影响的方位非常小,对钻铤外部的地层几乎没有影响.对比图15和图16可以看出,短源距的探测范围与探测深度明显比长源距小.此外,振幅比空间灵敏度分布与相位差空间灵敏度分布之间存在着明显差异,振幅比空间灵敏度的分布范围更大,其探测深度更大.
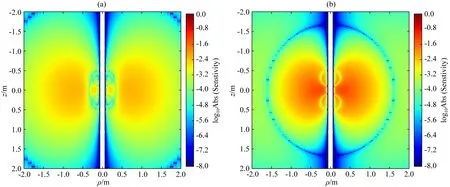
图15 短源距轴向感应电动势的振幅比与相位差空间灵敏度分布图(2 MHz)(a) 振幅比空间灵敏度; (b) 相位差空间灵敏度.Fig.15 Spatial sensitivity distribution of attenuation and phase shift of coaxial induced electromotive force in high frequency of 2 MHz for the short spacing(a) Spatial sensitivity of attenuation; (b) Spatial sensitivity of phase shift.
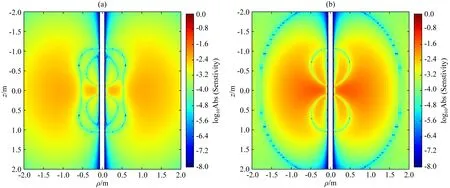
图16 长源距轴向感应电动势的振幅比与相位差空间灵敏度分布图(2 MHz)(a) 振幅比空间灵敏度; (b) 相位差空间灵敏度.Fig.16 Spatial sensitivity distribution of attenuation and phase shift of coaxial induced electromotive force in high frequency of 2 MHz for the long spacing(a) Spatial sensitivity of attenuation; (b) Spatial sensitivity of phase shift.
3 结论
本文利用混合法研究建立了环状刻槽钻铤情况下随钻方位电磁波测井响应的数值模拟方法,对环状刻槽中铁氧体磁导率以及地层电导率变化对各个线圈上感应电动势的影响特征进行了系统分析.数值结果显示,铁氧体磁导率的增大明显提高了发射线圈的发射功率,选择相对磁导率等于200的铁氧体已能够显著地提高发射效率以及各个接收器上感应电动势的强度.而在改进仪器发射效率的同时,铁氧体对周围的电磁场空间分布以及探测能力无明显影响,因此,在对共轴电磁响应进行处理时不需要考虑钻铤环状刻槽的影响.然而,对于共面电磁响应,环状刻槽以及铁氧体磁导率会对其产生较大影响,如何定量解释横向电磁有待更进一步的研究.
附录A
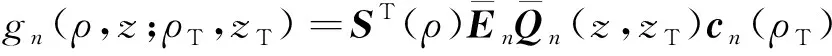
(A1)
(A2)
(A3)
其中,
(A4)
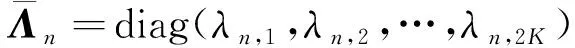
(A5)
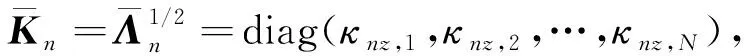
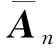
(A6)
附录B
将方程(17)简化成如下带状方程(Tamarchenko and Druskin, 1993;Wang and Yang, 2001):
(B1)
其中,
(B2)
(B3)
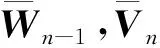
a)传播矩阵的递推运算
首先不考虑右端项的影响.利用条件U1=0和UN+1=0,可以得到地层界面n+1与地层界面n上的电场递推公式:
(B4)
其中,
(B5)
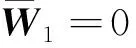
(B6)
其中,
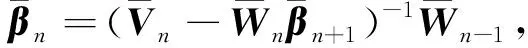
(B7)
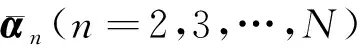
b)匹配矩阵递推算法
将(B4)和(B6)代入到方程(B1)中得到:
(B8)
其中,
(B9)
称为界面匹配矩阵.