基于电磁卫星的闪电哨声波智能检测算法的研究进展
2021-05-07袁静王桥张学民杨德贺王志国张乐申旭辉泽仁志玛
袁静, 王桥, 张学民, 杨德贺* , 王志国, 张乐, 申旭辉, 泽仁志玛
1 防灾科技学院, 河北 廊坊 062541 2 应急管理部国家自然灾害防治研究院, 北京 100085 3 中国地震局地震预测研究所, 北京 100036 4 清华大学, 北京 100084 5 中国电信股份有限公司研究院, 北京 102209
0 引言
高空闪电发生时产生宽频带电磁波,电磁波中含有高频成分和低频成分.由于频率高的群速度大,故高频成分比低频成分先到达,导致接收喇叭中出现下降的声调,像哨声一样,故称其为哨声波.有的哨声波,到达电离层后,沿着地磁力线传播(如图1所示)到达地球另一端共轭点,称之为短哨声波.还有一部分被电离层反射回到闪电发生地,称之为长哨声波(Chen et al., 1996).目前观测闪电哨声波主要有两种方式:地面甚低频(Very low frequency, VLF)观测站和空中飞行器.最著名的地面VLF观测站是电离层闪电全息成像阵列(张义军和张阳, 2016; Johnson, 2000),该阵列覆盖了美国中西部闪电影响的绝大部分区域,通过观测VLF信号,对闪电伴随的电离层的扰动进行深入研究,其研究主要涉及到闪电引起的电离层变化特征、观测方法、相互作用模式以及引起的中高层空间放电现象等方面(Johnson, 2000; Kucherov and Nikolaenko, 1979; Lay and Shao, 2011; Marshall et al., 2008a,b; Inan et al., 1991).因此,地面VLF观测站能够通过闪电哨声波现象研究闪电引起的电离层扰动,其缺点是地面观测站具有空间的局限性,且观测信号容易受到地面干扰,比如地铁、工地建设等人类活动的影响.卫星捕获的闪电哨声波避免了空间位置的限制且不容易受地面干扰影响,因此,基于电磁卫星的闪电哨声波更适合开展电离层方面的研究和探索.

图1 闪电哨声波传播路径Fig.1 Propagation path of a lightning whistler
1993年,地震电离层扰动理论的出现推动了地震电磁卫星的发展(Parrot et al., 1993).法国2001年正式对外公布 DEMETER卫星计划,2004年成功发射,2010年底停止运行.DEMETER卫星特定的轨道设计方案,使其成为全球第一颗专门用于地震和火山引起的电离层扰动监测的电磁卫星,是国际上地震电磁空间探测一个里程碑式的发展标志.随后,在经历了长期的科研论证后,中国于2013年正式启动电磁卫星计划,2018年2月2日,ZH-1卫星成功发射,2018年11月完成在轨测试,是国内首个地球物理场探测卫星,主要用于获取全球空间电磁场、电磁波、电离层等离子体、高能粒子沉降等科学数据,是提取与地震前兆相关的空间环境信息的重要观测手段.所获取的探测资料有利于地震电离层及空间物理相关现象研究的开展,成为世界同行关注的热点(申旭辉等, 2018; 张学民等, 2020).
ZH-1卫星的感应磁力仪(Wang et al., 2018)和电场探测仪(Huang et al., 2018a,b)均能捕获到闪电哨声波现象,其在VLF波段的电磁场数据的时频图中呈现的是色散状,如图2和图3所示.产生该形态特征的物理机制是:高频的电磁波传播的速度快,先到达;低频的电磁波的速度慢,后到达,反映在时频图上是频率随着时间逐渐减少,称之为“色散谱”.当路径长度较长或沿传输路径的电子密度较密集时,色散谱变大.由此说明,色散形态与传播路径的长度和传播路径中的等离子体的电子密度分布有关.除此之外,闪电哨声波在传播的过程中携带了其他大量的地球空间物理的相关信息,因此,电磁卫星的闪电哨声波是开展空间物理研究的重要媒介和手段.例如:Záhlava等(2018a)分析了DEMETER和RBSP对地球内部磁层哨声模式波的纵向依赖性的测量结果,结果表明等离子体层内部的哨声模式波的纵向依赖性很强.Bayupati等(2012)分析AKEBONO卫星观测到的闪电哨声波的色散形态,讨论了闪电哨声波沿轨道传播的时间与电子密度分布的关系,表明了闪电哨声波的色散趋势是确定等离子体层中整体电子密度分布的有力方法.Oike等(2014)分析了AKEBONO卫星探测到的闪电哨声波发生频率与地面观测到的闪电活动的空间分布和时间变化,表明了在电离层中闪电哨声波的出现与闪电活动以及地球周围的电子密度分布密切相关.Clilverd等(2002)使用全球闪电定位网(World-Wide Lightning Location Network, WWLLN)来确定闪电的来源位置,然后根据闪电哨声波的传播时间,远程感测电子密度分布频率,借助传播理论导出电子密度沿传播路径的函数.Parrot等(2019)通过闪电哨声波发现:全球温度变化1°,闪电发生频率变化5%~6%.Záhlava等(2018b)通过观测闪电哨声波色散形态的衰减程度发现晚上衰减慢,并得到晚间的空间电离层的浓度低的结论.此外,由于空中飞行的卫星的电子元件容易受高能电子的总剂量效应和单粒子效应影响而受损,借助哨声波数据构造哨声波参数统计模型,开展基于哨声波模型的高能电子通量预测,对卫星设计和防护具有重要的意义(Horne et al., 2013; 罗旭东等, 2017).

图2 张衡一号卫星闪电哨声波形态图例Fig.2 The time-frequency spectrogram of the lightning whistler observed by ZH-1 satellite
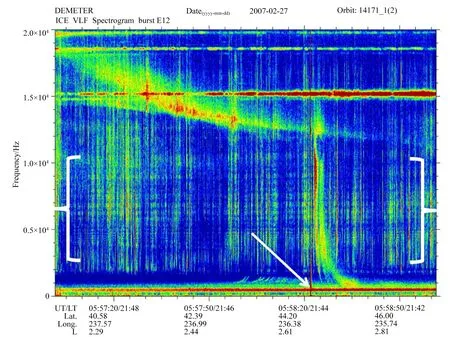
图3 DEMETER卫星闪电形态图例(Parrot et al., 2015)Fig.3 The time-frequency spectrogram of the lightning whistler observed by DEMETER (Parrot et al., 2015)
综上,电磁卫星能够捕获到大量的闪电哨声波,为借鉴闪电哨声波的形状特征和色散程度等开展地震电离层和空间物理研究提供了可靠的数据支撑.然而,目前通过人工识别闪电哨声波现象的方式阻碍了相关研究的进展(Ferencz et al., 2001;Lichtenberger et al., 2008),其主要原因是:
(1)电磁卫星高精度和全天候的工作模式导致电磁卫星存档的数据体量很大,比如ZH-1卫星日产的数据量高达20 G.
(2)闪电频发使得电磁卫星捕获的闪电哨声波现象的数量很大.闪电是在地球空间发生最为频繁的一种自然现象,1925年,Brooks等(1925)使用雷暴日资料,估计全球在任一时刻存在1800个闪电.2003年Christian指出全球闪电每秒钟45次.此外,据WWLLN(http:∥www.wwlln.com/)记载:仅2017年闪电发生了2.08亿次.2019年7月28日,全球闪电分布如图4所示,发生雷电约64万个.
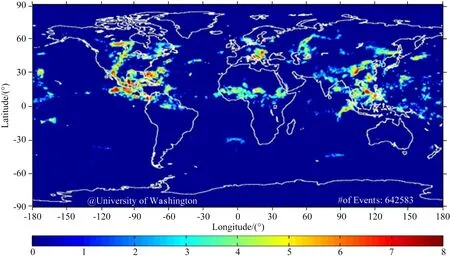
图4 2019年7月28日全球闪电密度分布图 (http:∥dudwlln.otago.ac.nz/)Fig.4 A global lightning density map on July 28, 2019 (http:∥dudwlln.otago.ac.nz/)
面临数据层面的挑战,近年来,随着计算机视觉和深度学习等技术的发展,国内外学者借助人工智能技术开始了从电磁卫星数据中自动检测闪电哨声波的研究,闪电哨声波传播的物理机制决定了其在时频图中特征是具有明显的色散形态,闪电哨声波智能检测的目标是从时频图中识别色散形态并进行定位.该问题的本质属于计算机视觉中的目标检测问题.目前发表的基于闪电哨声波智能检测算法涉及到空间物理、信号处理、图像处理、模式识别和机器学习等多学科交叉,并取得了一定的效果.
本文将对闪电哨声波智能检测算法进行整理和对比分析,创新点主要体现在:首次综述基于电磁卫星数据的闪电哨声波智能检测算法,对不同的算法进行分类整理和分析,为开展基于人工智能技术的海量电磁卫星数据处理提供参考.全文的内容组织安排如下:第一节介绍闪电哨声波的时频特征和类型;第二节介绍智能检测算法的基本内容,分别从特征提取、分类(识别)和定位三个方面对不同的算法进行整理和对比分析;第三节介绍智能检测算法的评价标准;第四节对部分算法进行复现;第五节总结当前闪电哨声波智能检测算法的现状,展望闪电哨声波智能检测研究的发展趋势和应用前景.
1 闪电哨声波的时频特征和类型
目前,人工识别电磁数据中的闪电哨声波的过程通常包含三个环节:对电场数据/磁场数据进行预处理;采用重叠的快速傅里叶变换将预处理后的数据转化成时频图;在时频图中,寻找色散形态区域.以此为依据,在DEMETER卫星中发现了大量的闪电哨声波的降调形态(Helliwell, 1965; 胡云鹏等, 2020; Santolík et al., 2009),如图3所示.Helliwell(1965)根据色散程度将地面VLF观测站观测到的闪电哨声波分为8种不同的类型,如表1所示.Santolík等(2009)指出地面VLF观测站记录的闪电形态与卫星观测到的闪电形态极其相似且均具有频散特性.不同类型的闪电哨声波均与闪电源、传播路径的长短、电子密度等物理空间环境有关,是探测等离子层及辐射带的重要媒介.值得注意的是目前的闪电哨声波识别算法均适用于识别单条线的闪电哨声波类型.
2 闪电哨声波智能检测算法
闪电哨声波自动识别最早可追溯到2008年,Lichtenberger等(2008)指出通过哨声波监测等离子体层电子密度变化遇到的瓶颈问题是需要大量人力从观测数据中去提取和辨识哨声波并分析哨声波的轨迹.因此,作者在蒂豪尼15个地面观测站的数据的基础上,提出了一个自动检测哨声波的算法(Automatic whistler detector and analyzer system, AWD).该方法开辟了闪电哨声波智能检测算法的先例,并比较成功的应用到从地面VLF观测站中自动识别闪电哨声波,该方法对于识别分数跳(表1中的第8个类型)的闪电哨声波效果较佳.
闪电哨声波智能检测算法的本质是属于计算机视觉中的目标检测,旨在从图像中寻找感兴趣的区域,提取该区域的特征,准确判断该特征的类别,并进行定位.因此,完整的闪电哨声波智能检测算法的流程如图5所示:(1)收集电磁场数据,通常是VLF波段的电场或磁场波形数据,如图6所示;(2)对数据进行滤波等预处理;(3)采用快速傅里叶变换处理电磁场数据得到时频图,如图7所示;(4)采用特征提取方法从时频图中提取能够表示闪电哨声波的特征;(5)对提取到的特征进行分类(识别);(6)用边界框对识别的目标进行定位.
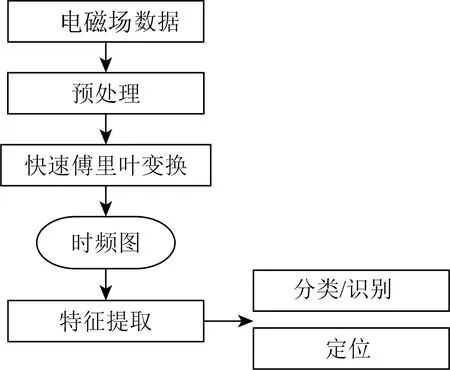
图5 闪电哨声波智能检测的流程Fig.5 The overall flow chart of the lightning whistlers detection

图6 张衡一号感应式磁力仪测得的快速变化磁场数据Fig.6 The fast variation data of geomagnetic field obtained by Search Coil Magnetometer onboard ZH-1 satellite
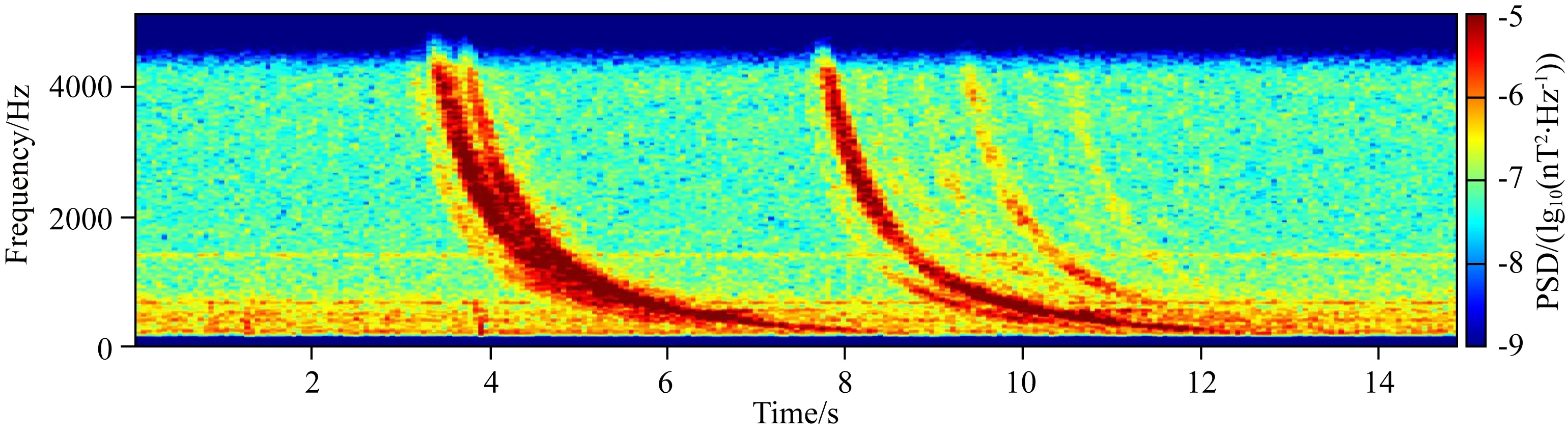
图7 张衡一号感应式磁力仪快速变化磁场数据的时频图Fig.7 The time-frequency spectrogram of the Search Coil Magnetometer data in Fig.6
在上述流程中,闪电哨声波的特征提取、分类(识别)和定位是算法的核心环节.接下来分别从特征提取、分类(识别)和定位三个方面对现存的智能检测识别算法进行梳理和对比.
2.1 特征提取
特征提取是计算机视觉智能识别过程中的关键环节.其主要作用是将智能模型不能识别的原始数据转化为智能模型可以识别的数值特征的过程.比如说,图像是由一系列像素点 (原始数据) 构成的,这些像素点本身无法被智能模型直接使用,需要将这些像素点转化成角点、纹理等形式(数值特征),供智能模型使用.特征的好坏对泛化性能有至关重要的影响(周志华, 2016).对闪电哨声波进行特征提取旨在数值化闪电哨声波的色散形态特征.本小节分别从人工提取特征和自动提取特征两个方面进行整理和对比分析.
2.1.1 人工提取特征
所谓人工提取特征是根据人工分析并结合相关的处理手段提取特征的过程.由于闪电哨声波具有明显的色散形态,The Stanford VLF Group(2018),Fiser等(2010),Oike等(2014),Ali Ahmad等(2019)和Dharma等(2014)采用图像处理技术来提取闪电哨声波的形态特征.The Stanford VLF Group(2018)针对DEMETER卫星的闪电哨声波,提出的特征提取方法是:对时频图(如图8所示)进行去噪处理和网格划分,如图9所示,然后计算每个网格中的平均幅度值,得到如图10所示的特征表示.

图8 时频图(The Stanford VLF Group, 2018)Fig.8 The time-frequency spectrogram (The Stanford VLF Group, 2018)
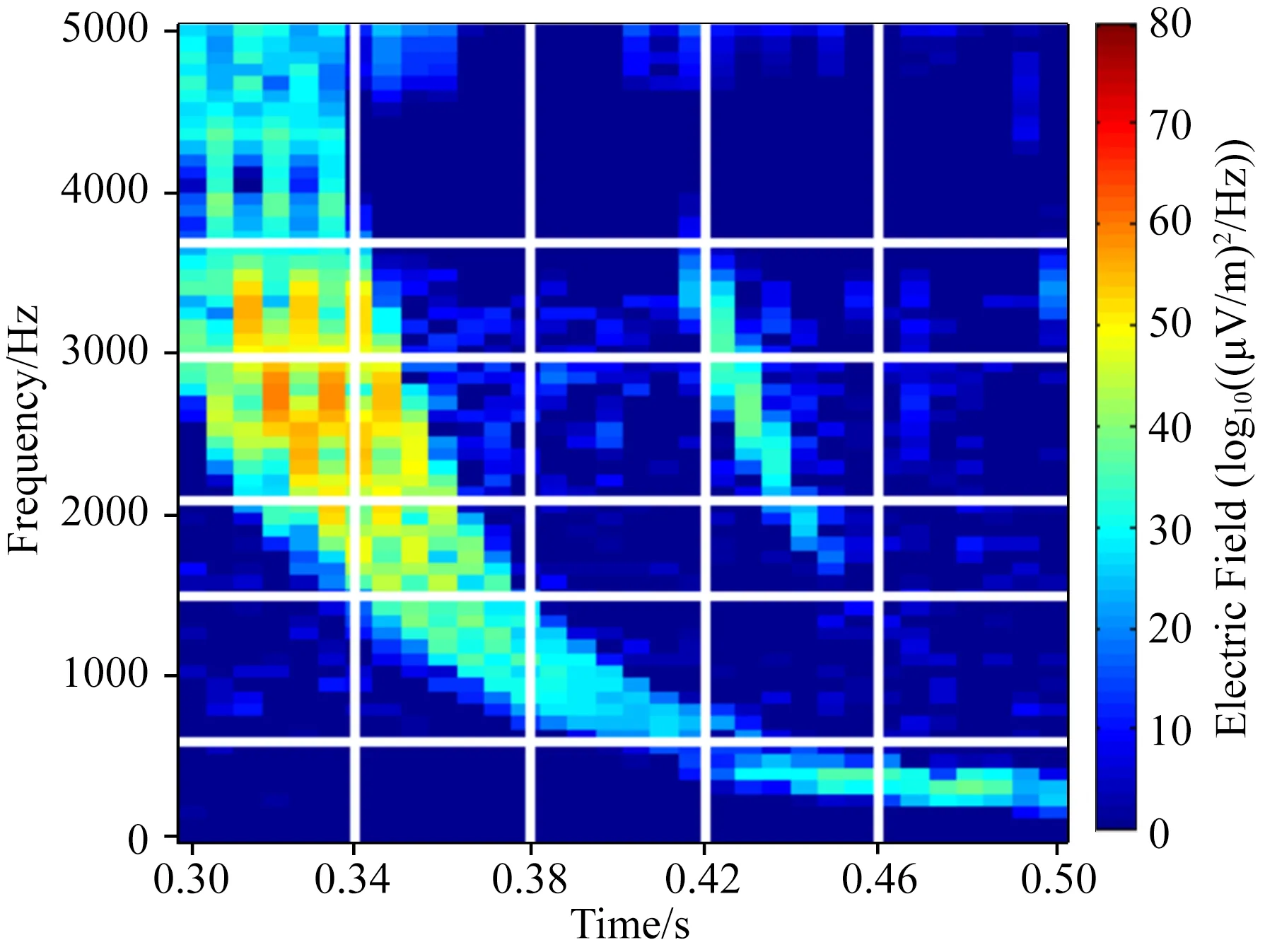
图9 去噪和网格化(The Stanford VLF Group, 2018)Fig.9 Denoising and meshing (The Stanford VLF Group, 2018)
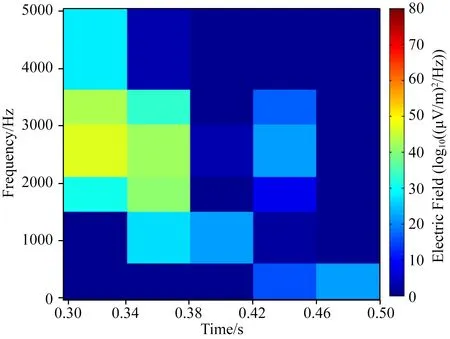
图10 合并(The Stanford VLF Group, 2018)Fig.10 Binning (The Stanford VLF Group, 2018)

图11 灰度化的时频图(Dharma et al., 2014)Fig.11 Grayscale image of the time-frequency spectrogram (Dharma et al., 2014)

图12 二值化处理后的时频图(Dharma et al., 2014)Fig.12 Binary image of the time-frequency spectrogram (Dharma et al., 2014)

图13 中值滤波和开运算处理后的时频图(Dharma et al., 2014)Fig.13 The results by median filter and open operation (Dharma et al., 2014)

图14 连通域标记(Dharma et al., 2014)Fig.14 Labeling the connected domain (Dharma et al., 2014)
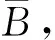
R=(x0,y0,w,h),
(2)
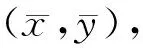
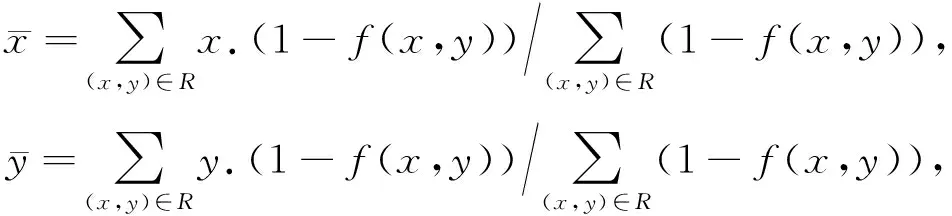
(3)
其中f(x,y)表示位置(x,y)的像素值,在本实例中其有两种取值0和1.其目标区域是0,背景区域是1.(5)本方法检测的是单条谱线的闪电哨声波.当找到所有的连通区域后,发现不含闪电哨声波的连通区域具有非常少的连通像素,因此,用下列筛选方法删除非闪电哨声波的连通区域.筛选方法是:统计每个连通区域的目标像素的数量,该值小于某阈值时,相应的连通区域和矩形框被删除,剩下的矩形框标记的连通区域即为检测到的闪电哨声波区域.此时,若依然存在两个重叠的矩形框,则意味着存在两个连通区域,这两个区域相互之间不连通且两个连通区域的重心不同,表示是两个不同的单条谱线的闪电哨声波.
该方法适合检测单条谱线的闪电哨声波,其缺陷是容易将相近的两个闪电哨声波识别为一个闪电哨声波.
上述闪电哨声波智能检测算法的特征提取依赖人工定义.这些方法与传统的计算机视觉的目标检测算法类似.在传统的计算机视觉的目标检测中,通常人工提取的特征包括尺度不变特征(Scale Invariant Feature Transform)(Lowe, 2004; Cai et al., 2015),哈尔特征(Viola and Jones, 2001)等,针对提取的特征,再采用AdaBoost(Adaptive Boosting)(Zhang et al., 2016)和DPM(Deformable Parts Model)(Felzenszwalb et al., 2008)等方法对特征进行分类(识别),其识别结果受特征的影响较大(Pei et al., 2016).因此,基于人工定义特征提取的闪电哨声波智能检测算法,最大的局限性是难以获得鲁棒性强的特征,对时频噪声十分敏感.
2.1.2 自动提取特征
自动提取特征旨在采用机器学习的方式由计算机自动从数据集中获取特征.LeCun等(2015)在利用深度神经网络自动提取图像特征方面取得了一系列的突破.从此,基于深度卷积神经网络的目标检测越来越引起业界的重视(Liu et al., 2018).鉴于深度神经网络具有强大的自动提取特征的能力,Konan等(2020)提出了两种基于深度卷积神经网络的闪电哨声波的特征提取方法:基于滑动深度卷积神经网络的闪电哨声波算法(Sliding Deep Neural Convolutional Neural Network, SDNN)(Konan et al., 2020)和基于YOLOV3 (You Only Look Once and Version 3rd, YOLOV3)目标检测网络的闪电哨声波算法(Konan et al., 2020),并公开了其源码(https:∥github.com/Kojey/MSc-whistler-waves-detector).
滑动深度卷积神经网络的闪电哨声波特征提取:主要的优势是其卷积层具有强大的特征学习能力.由于闪电哨声波具有简单的形状,提出了三个卷积层的卷积神经网络对其进行特征提取.该网络有两个主要组成部分:卷积层和分类层,如图15第1~3层所示为卷积层:第1层和第2层的卷积层具有卷积单元和池化单元:卷积单元负责提取图像中的局部特征,第一层卷积单元有2个卷积核,第二层的卷积单元有4个卷积核;池化单元用来大幅降低参数量级(降维)防止过拟合;第3层的卷积层有8个卷积核,无池化层.全网络结构共14个卷积核,主要作用是提取图像的局部特征.
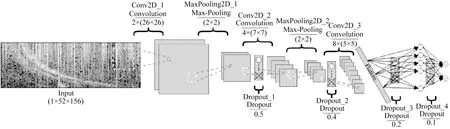
图15 滑动的深度卷积神经网络(Konan et al., 2020)Fig.15 Sliding deep convolutional neural networks (Konan et al., 2020)
图16为卷积神经网络模型学习到的卷积核及其相关的特征图:图16a是训练得到卷积神经网络模型后,显示了该模型的第一层的两个卷积核、第二层的四个卷积核以及第三层的8个卷积核;卷积核提取的特征都具有相同的功能(梯度递减的线),但在卷积核中的位置不同;此外,卷积核提取的特征具有明显的特征相似性,其原因是哨声波的形态特征除了色散状没有明显的其他形状特征;第三层的卷积核提取的特征的分辨率低,其主要原因是随着网络的深入,学习到的特征更加复杂且不容易理解.图16b显示的是应用卷积神经网络模型提取闪电哨声波特征,可以清楚地观察到原始哨声波的形状.图16c显示的是应用卷积神经网络模型提取非闪电哨声波的特征,没有观察到明显的形状.

图16 卷积层的输出(Konan et al., 2020)(a) 训练得到的卷积核; (b) 卷积核提取的闪电形态特征; (c) 卷积核提取的非闪电形态的特征.Fig.16 Output of convolutional layer (Konan et al., 2020)(a) Filters of the trained neural network; (b) Feature maps when detecting whistlers; (c) Feature Maps when detecting noise.
基于YOLOV3深度神经网络的闪电哨声波特征提取:借鉴YOLOV3深度神经网络的特征学习能力,Konan等(2020)直接利用YOLOV3网络训练闪电哨声波数据集,其过程包括:将闪电哨声波波形数据预处理后转化为时频图,对时频图进行图像标注,在标注的数据上训练神经网络YOLOV3.YOLOV3的特征提取是目前最优的特征提取方式,由Redmon等(Redmon et al., 2016; Redmon and Farhadi, 2017, 2018)提出.网络模型结构图如图17所示:此结构主要由75个卷积层构成,卷积层对于分析物体特征最为有效.由于没有使用全连接层,该网络可以适应任意大小的输入图像.此外,在YOLOV3中没有出现池化层,取而代之的是将卷积层的步长设为2来达到下采样的效果,同时将尺度不变特征传送到下一层.其自动提取特征的优势体现在YOLOV3中使用了残差结构(对应着在上面的YOLOV3结构图中的Residual Block).残差结构是由一系列卷积层和一条短路径组成,如图18所示.随着网络越来越深,学习特征的难度也就越来越大,之前的卷积神经网络是直接学习特征x,加入短路径后变成在之前学习的特征的基础上添加某些特征F(x),以此获得更为鲁棒的特征H(x)=F(x)+x(Redmon and Farhadi, 2018).该策略使得机器学习的目标从学习完整的特征变成学习残差特征,极大地降低了学习鲁棒特征的难度.

图17 YOLOV3的网络结构(Redmon and Farhadi, 2018)Fig.17 The network structure of YOLOV3 (Redmon and Farhadi, 2018)

图18 YOLOV3的残差网络(Redmon and Farhadi, 2018)Fig.18 The residual network in the network structure of YOLOV3 (Redmon and Farhadi, 2018)
基于SDNN网络的闪电哨声波检测模型和基于YOLOV3网络的闪电哨声波检测模型的调参过程将在第4.2.2小节进行阐述,模型的训练过程将在第4.3小节进行介绍.
2.2 分类/识别
分类旨在通过设计算法为提取的特征分配类别标签,通常也叫识别.闪电哨声波分类算法的目标是对上节提取的特征进一步判断其是闪电哨声波或不是闪电哨声波.本小节将现有的闪电哨声波的分类算法分为两类:基于模板匹配的分类算法和基于神经网络的分类算法.分别从这两个方面进行整理和对比分析.
2.2.1 基于模板匹配的分类
由于闪电哨声波具有明显的色散形态,The Stanford VLF Group(2018),Fiser等(2010),Ali Ahmad等(2019)和Oike等(2014)在提取的闪电哨声波形态特征的基础上,采用模板匹配的方式对闪电哨声波的特征进行分类识别.首先:根据闪电哨声波的色散形态制作模板,计算待识别区域与模板之间的相似度,当其达到某个阈值时,认为该区域是闪电哨声波,否则视为没有闪电哨声波.
The Stanford VLF Group(2018)制作的闪电哨声波的模板,是采用格子化的手段对图像进行降采样处理,得到如图10相似的模板.用模板与待检测的区域进行卷积计算得到相似度度量的值,以此阈值作为分类标准,高于该阈值,判断待测区域为闪电哨声波.
Fiser等(2010)提出闪电哨声波的色散符合Eckersley公式(Gurnett et al., 1990),t=Df-0.5,其中D是色散率,t是频率f的波到达的时间.同时指出白天和晚上的色散状态存在差异,则其制作两个哨声波模板.如图19所示的是白天的哨声波模板,时间宽度0.4 s,再按照同样的方法得到晚上的哨声波模板,模板记为b.然后,从电场波形数据中提取0.4 s的波形数据,做重叠短时傅里叶变换得到频谱图,用a表示,接着按照下列公式(4)计算互相关函数得到互相关值.最后采用阈值判断互相关值最大的地方,即为检测到的闪电哨声波,如图20所示.
(4)
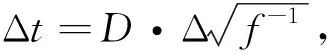
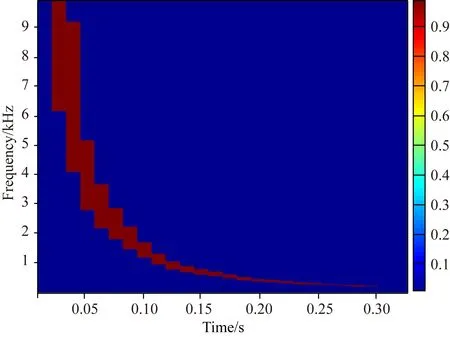
图19 闪电哨声波模板(Fiser et al., 2010)Fig.19 Lightning whistler template (Fiser et al., 2010)
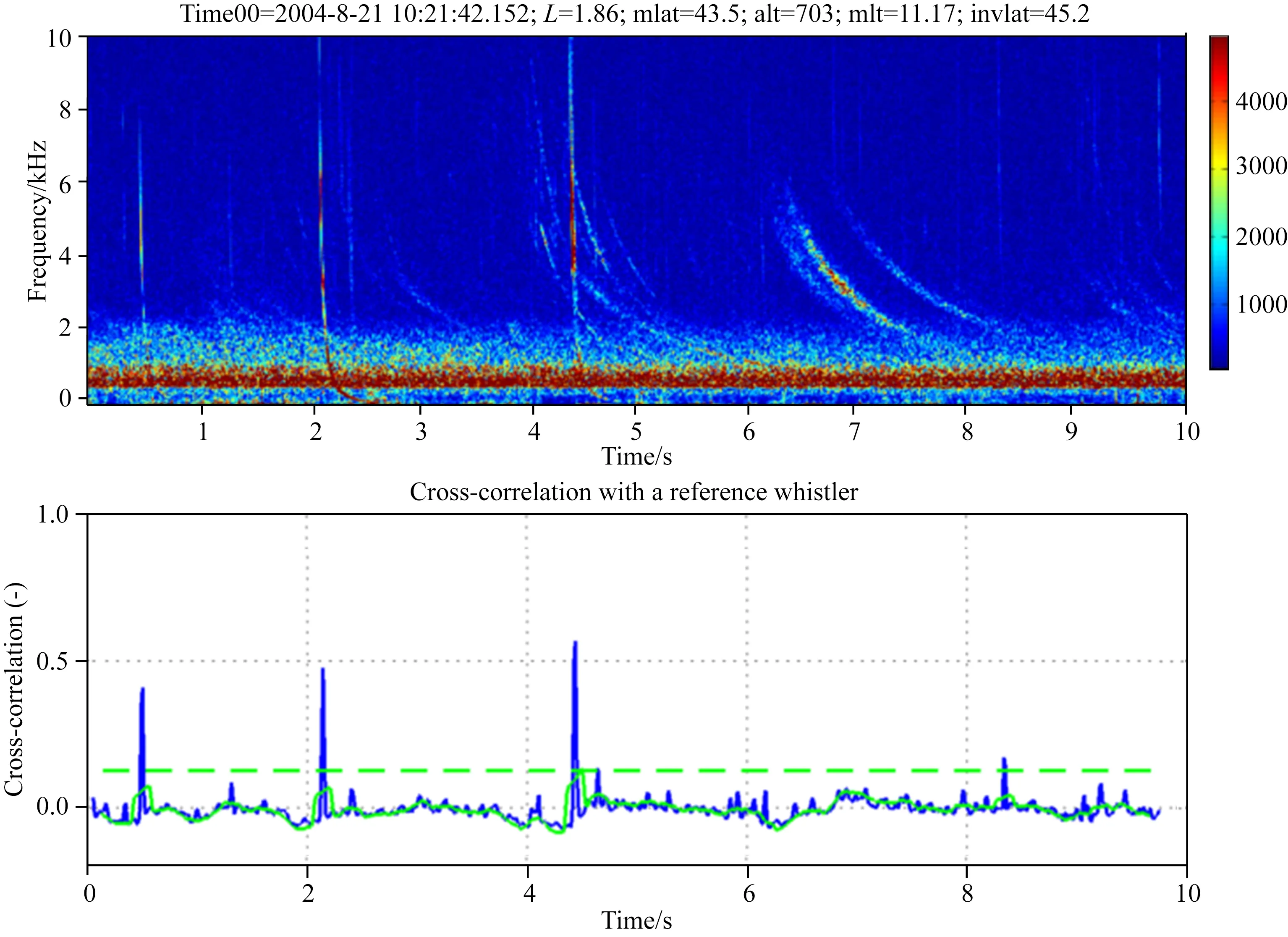
图20 基于互相关熵的闪电哨声波自动检测(Fiser et al., 2010)Fig.20 Automatic detection of lightning whistler with cross-correlation entropy (Fiser et al., 2010)
当上述30个频带中的6个频带与其中一个直线匹配时,被判定为潜在的闪电哨声波;当同时检测到多个潜在哨声波重叠时,从潜在哨声中选出最匹配的一个,其结果如图22所示.

图21 时间变化与频率之间的关系图(Oike et al., 2014)Fig.21 Relationship between time and frequency (Oike et al., 2014)

图22 检测闪电哨声波的结果(Oike et al., 2014)Fig.22 Detection results of lightning whistler (Oike et al., 2014)
Ali Ahmad等(2019)认为根据Eckersley公式制作的模板,能够识别近似直线的闪电哨声波,无法识别诸如鼻型、长型等类型的哨声波,则提出了利用曲线检测和模式规则结合的哨声波识别方法.再用Bresenham线检测算法检测线(Bresenham, 1977),利用如图23所示的决策方案识别6种不同类型的闪电哨声波.
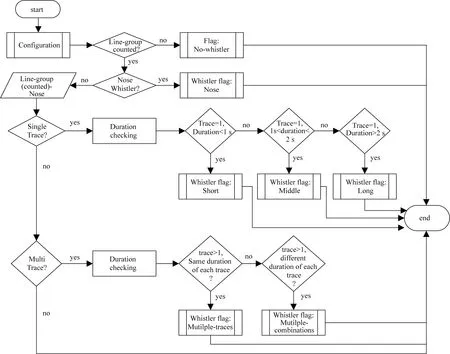
图23 决策规则(Ali Ahmad et al., 2019)Fig.23 Decision Rules (Ali Ahmad et al., 2019)
2.2.2 基于神经网络的分类
基于SDNN的分类器(Konan et al., 2020):如图24所示,其分类环节是由最后两层完成,包含128个神经元的全连接层和2个神经元的输出层.为防止过度拟合,在分类环节增加了2个Dropout层,联合前面的3个卷积层和2个池化层,整个网络共有522112个可训练参数.

图24 滑动的三层深度卷积神经网络 (Konan et al., 2020)Fig.24 Sliding three-layer deep convolutional neural network (Konan et al., 2020)
基于YOLOV3深度卷积神经网络的分类方法:在传统的深度卷积网络中利用不同深度的特征直接分类,小的物体会在相对较大的特征图中被识别出来,而大的物体会在相对较小的特征中被识别出来,从而达到对应不同尺度的物体的目的.然而在实际应用中,不同深度所对应的特征图包含的信息不同,导致在不同级别的特征中进行目标检测的精度不够.为了克服该问题,YOLOV3采用了多尺度融合(Feature Pyramid Networks, FPN)技术,如图25所示:采用上采样(Upsample)和融合做法,融合了3个尺度(13×13、26×26和52×52),在多个尺度的融合特征图上分别独立做检测,使得对小目标的检测效果得到明显提升.此外,其输出层的激活函数用逻辑回归替换了传统的softmax,输出结果由类别标签变为类别的概率.
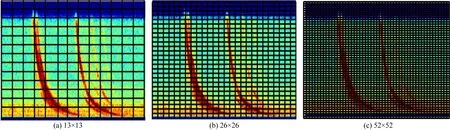
图25 FPN特征融合: (a) 13×13; (b) 26×26; (c) 52×52.Fig.25 FPN fusion
基于SDNN网络的闪电哨声波检测模型和基于YOLOV3网络的闪电哨声波检测模型的调参过程将在第4.2.2小节进行阐述,其训练过程将在4.3小节进行介绍.
2.3 定位
闪电哨声波智能检测算法中的定位方法主要有两种:滑动窗方法和智能判断方法.The Stanford VLF Group(2018),Fiser等(2010),Ali Ahmad等(2019)和Oike等(2014)提出的定位方法与Konan等(2020)提出的滑动卷积神经网络的闪电哨声波检测的定位方法均采用的是在时频图中滑动固定时间长度的窗,然后对窗内的区域进行特征提取和分类,该定位策略主要针对单条频谱曲线的闪电哨声波类型,且这些闪电哨声波图像区域的宽度相差不大,该方案无法检测多个闪电源的闪电哨声波和单个闪电源的多条频谱曲线构成的闪电哨声波的类型.通常,多个闪电源的闪电哨声波类型包含多条频谱曲线,若多条频谱曲线均由每个闪电源的第一跳的哨声波频谱曲线组成,则每条频谱曲线的强度都较大,反映在图像上的特点是多条频谱曲线的颜色/亮度差别不大;若多条频谱曲线是由每个闪电源的多跳的哨声波频谱曲线组成,则频谱曲线的频谱强度存在差异和变化,这种差异会周期性出现,反映在图像上的特点是颜色/亮度差异随着时间的变化而周期性出现.而单个事件的多条频谱曲线的闪电哨声波类型也包括多条频谱曲线,但频谱曲线的频谱强度随着时间发生变化,时间滞后的频谱曲线其频谱强度逐渐变小,反映在图像上的特点是其颜色/亮度逐渐变淡.针对频谱曲线的强度随时间变化的特点,可采用计算机视觉处理技术提取上述频谱强度等信息,并进一步探索新方法,使其适用于检测多闪电源的多频谱曲线的闪电哨声波和单闪电源的多频谱曲线的闪电哨声波.
基于YOLOV3深度神经网络闪电哨声波智能检测算法 (Konan et al., 2020)采用的定位方法:其数学模型中融合了定位、特征提取和分类.位置的数学模型,如图26所示.其中tx,ty,tw,th表示模型的预测输出,cx和cy表示网格单元的坐标,pw和ph表示预测前边界框的尺寸,bx,by,bw,bh就是预测得到的边界框的中心坐标和尺寸,坐标的损失函数采用平方误差.δ(tx)和δ(ty)表示在x轴和y轴上预测得到的边界框的中心坐标相对于网络单元坐标的距离.
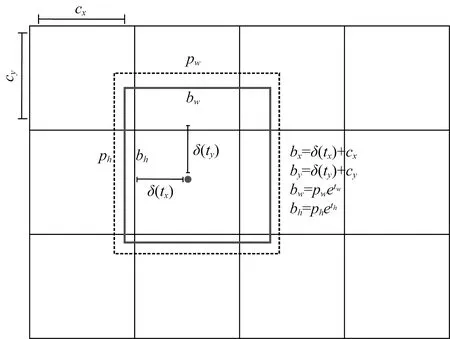
图26 YOLOV3 坐标模型 (Redmon and Farhadi, 2018)Fig.26 Coordinate representation in mathematical model of the YOLOV3 (Redmon and Farhadi, 2018)
3 评价指标
评估闪电哨声波智能检测算法通常需要用到基准数据,目前采用的基准数据主要是欧洲闪电探测网(http:∥www.euclid.org)和全球闪电定位网络(http:∥www.wwlln.com/)的数据.在基准数据的基础上,其评价指标主要有四种:错分率、虚警率、漏检率和F1值.四种指标从不同的角度评价了智能检测模型的性能(杨德贺等, 2018).
设闪电哨声波是正类样本(Positive,P),非闪电哨声波是负类样本(Negative,N),接下来将阐述四种指标的定义.首先,符号定义如表2的混淆矩阵.
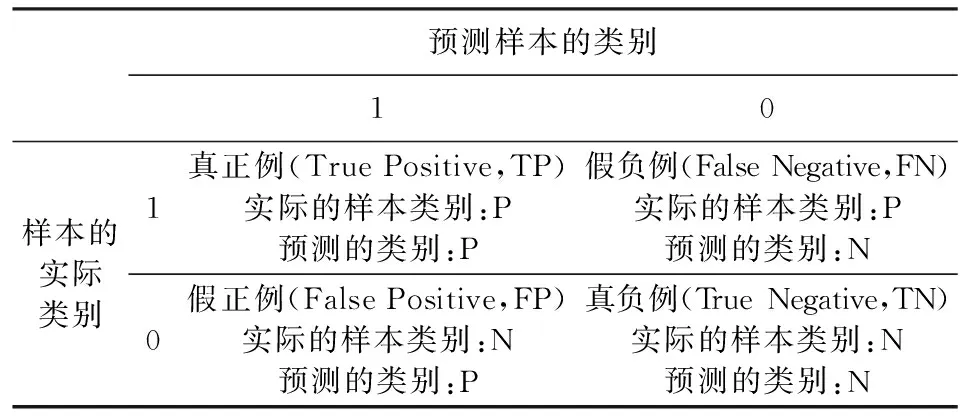
表2 矩阵Table 2 Matrix
NTP表示真正例的样本的数量;NFN表示假负例的样本的数量;NFP表示假正例的样本的数量;NTN表示真负例的样本的数量;四种评价指标的定义如下:
(1)错分率=(NFP+NFN)/(NTN+NTP+NFP
+NFN) .
(5)
含义:在所有待检测的数据中,误识别的数据量所占的比例,通常该指标越小越好.
(2)虚警率=NFP/(NFP+NTP),
(6)
含义:在所有检测到的闪电哨声波的数据中,将非闪电哨声波误判为闪电哨声波的数据所占的比例.
(3)漏检率=NFN/(NTP+NFN),
(7)
含义:在所有已知的闪电哨声波的样本中,将闪电哨声波误判为非闪电哨声波所占的比例.
(4)F1值(F1-Score)
=2/(1/Precision+1/Recall),
(8)
其中:Precision表示准确率,准确率=NTP/(NTP+NFP):其含义是预测正确的图片个数占总的正类预测个数的比例,该指标越大越好;Recall表示召回率,召回率=NTP/(NTP+NFN):其含义是确定正类被预测为正类图片占所有标注图片的个数,该指标越大越好.通常情况下,准确率高,召回率就低,召回率高,准确率就低.指标F1-Score综合考虑准确率和召回率的调和值.
目前评价闪电哨声波智能检测效果的定量指标如表3所示.通过表3发现,在闪电哨声波智能检测性能的评价指标方面,更注重的是错分率和虚警率.同时,本文认为漏检率亦重要.
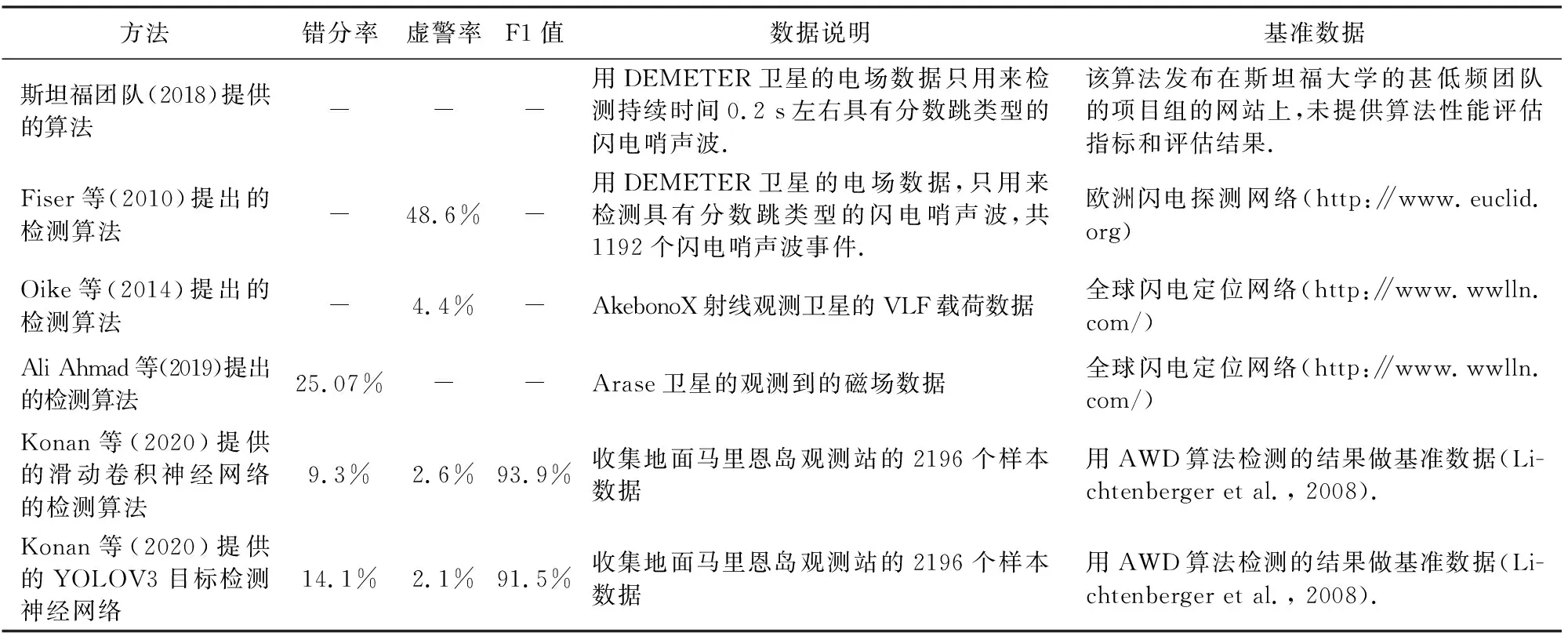
表3 闪电哨声波检测算法的性能指标比较Table 3 Performance indexes for lightning whistler detection algorithm
虚警率:基于神经网络学习到的闪电哨声波的特征具有抽象和强鲁棒的特点,强鲁棒通常意味着学习到的特征具有旋转不变性.比如,将图27a分别旋转了90°、180°和270°后则得到图27(b—d),再将图27(a—d)分别输入到YOLOV3网络后获取的特征是相同的.因此,若时频图中的非闪电哨声波的空间现象呈现的形状特征与闪电哨声波呈现的形状特征具有旋转相似性,如图28a所示:其矩形框内的图像不是闪电哨声波,但其色散状特征旋转180°后与闪电哨声波色散状极其相似,因此容易被误识别为闪电哨声波,致其虚警率升高,同时错分率增加.
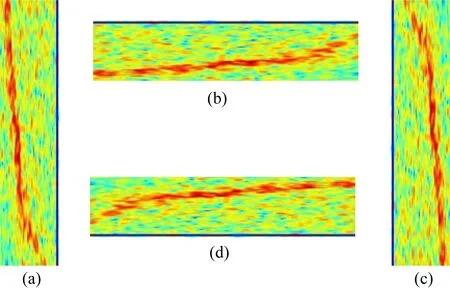
图27 旋转不变性(a) 原图; (b) 逆时针旋转90°; (c) 逆时针旋转180°; (d) 逆时针旋转270°.Fig.27 Rotation invariance(a) Original image; (b) 90° anticlockwise rotation; (c) 180° anticlockwise rotation; (d) 270° anticlockwise rotation.
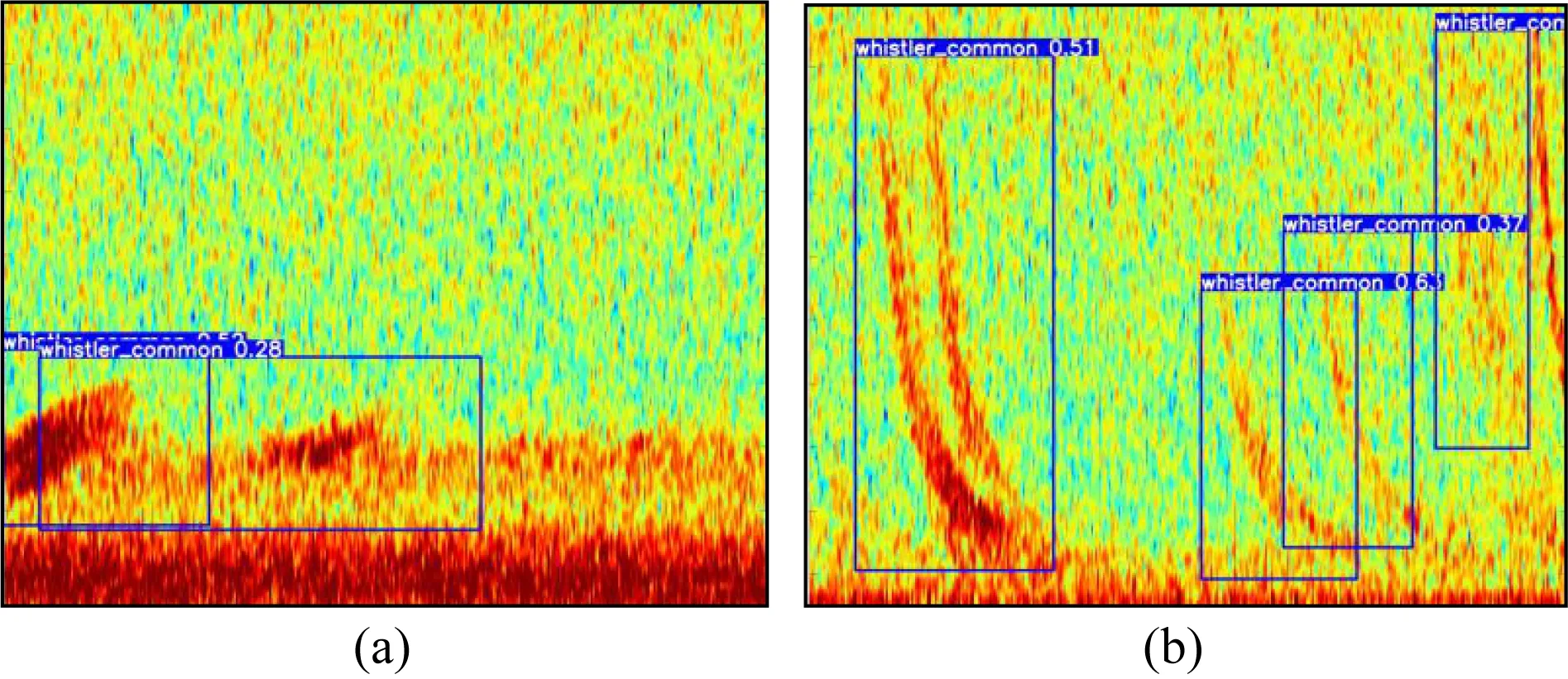
图28 实例(a) 虚警实例; (b) 漏检实例.Fig.28 An example(a) False alarm; (b) Undetected.
漏检率:若时频图中的闪电哨声波比较密集,如图28b所示最左边的矩形框内有两条闪电哨声波,但由于密集,导致只识别出一条闪电哨声波,致使漏检率增加,同时错分率增加.
除此之外,错分率、虚警率和漏检率具有以下意义:闪电哨声波的检测结果通常被用来做进一步的研究.闪电哨声波智能检测模型的错分率综合评价了采用该模型自动检测闪电哨声波的可靠性.错分率低意味着模型检测的效果比较可靠,即采用该模型检测出电磁卫星数据中的闪电哨声波后,可以直接使用检测出的结果开展下一步研究.而若错分率高,则意味着需要人工对识别结果进行复检,以纠正错分的数据,但错分率难以指明复检的方向.而虚警率和漏检率恰恰可以指出复检的方向.若虚警率高则意味着需要人工进一步从检测到的闪电哨声波的样本中进行复检以剔除将非闪电哨声波识别为闪电哨声波的数据.若漏检率高意味需要人工进一步从原始数据中复检被遗漏的闪电哨声波.这些复检工作对于进一步做闪电哨声波的研究具有十分重要的作用.
4 现有的闪电哨声波检测算法在张衡卫星数据上的效果
闪电哨声波智能检测方法通过特征提取、分类和定位等过程实现了自动检测闪电哨声波的功能.由于特征提取是闪电哨声波分类和定位的前提,本节将现有的闪电哨声波智能检测算法按照特征的提取方式分为两类:基于人工定义特征的智能检测算法和基于神经网络自动提取特征的智能检测算法.并从中选择了三种具有代表性的算法在张衡一号卫星的数据上进行了复现.如图29所示.在基于人工定义特征的智能检测算法中,选择基于形态学处理的智能检测算法(Dharma et al., 2014);在基于神经网络自动提取特征的智能检测算法中,分别选择SDNN网络(Konan et al., 2020)和YOLOV3网络的智能检测算法(Konan et al., 2020).接下来,将分别从数据介绍,代表性算法的参数设置,代表性算法的模型训练和代表性算法的效果四个方面进行阐述.

图29 三种代表性的算法Fig.29 Three typical algorithms
4.1 数据介绍
利用2018年8月份张衡卫星感应磁力仪VLF频段Z分量的波形数据.以每2 s窗口且重叠90%的方式进行傅里叶变换生成时频图,用这些时频图创建数据集,仅关注时频图中的单个色散形态的闪电哨声波.使用深度神经网络常用的策略是构建较小的超参数训练集,在其上尽量进行过拟合训练寻找最佳的参数组合,当超参数选择确定后再在模型训练集上训练模型,最后再在测试集上对该模型进行评价.因此,将张衡卫星的数据分为三类:超参数训练集含有1000条闪电哨声波数据(用来选择模型的超参数);模型训练集含有2098条闪电哨声波数据(超参数选定后用来训练模型);模型测试集含25834条闪电哨声波(用来测试模型的效果),均为单个频谱线的闪电哨声波.
4.2 代表性算法的参数设置
4.2.1 基于人工定义特征的智能检测算法
本小节主要介绍基于形态学处理的闪电哨声波检测算法中每个环节中的参数设置情况.首先将原始时频图进行灰度化处理;再采用阈值分割进行二值化处理,该过程中的阈值分割算法采用自适应阈值分割算法(Otsu, 2007);然后,进行中值滤波处理,该过程中采用的窗口大小是5×5;接着,进行开运算处理,该环节采用的结构算子是5×5的圆形结构算子;再提取连通域,用矩形框对其进行标记,用星号标记其重心位置;最后,统计连通域中的目标像素,当目标像素总量大于某阈值时,保留该连通域的矩形框,否则将删除该连通区域的矩形框,该环节中的阈值是40.
4.2.2 基于神经网络自动提取特征的智能检测算法
目前,神经网络具有自动地学习鲁棒特征的能力且效果最优,但其检测效果依赖于神经网络模型的性能,该性能与训练过程中的超参数的设置有关.其涉及的超参数主要有5种:学习率(learning rate或作lr),批次大小(batch_size),激活函数(activation),轮次(epoch)和优化器(optimizer).在深度神经网络中,上述5种超参数之间存在比较强的耦合性,使得寻找最优的超参数组合更困难.常用的方法是在超参数训练集上进行训练进而获取最佳的超参数组合,当超参数选择确定后再在模型训练集上训练模型,最后在测试集上对训练好的模型性能进行评估.本小节将以基于SDNN网络的闪电哨声波检测模型为例介绍超参数调整的过程.
学习率(lr):指在优化算法中沿损失梯度的反方向更新网络权重的幅度大小.学习率过大导致模型(在最优点附近)震荡抑或不收敛;学习率过小则导致模型收敛速度偏慢,需要更长的时间训练.学习率参数的调整需要结合优化器等参数.
轮次(epoch):1轮次指的是完整的数据集通过了一次神经网络的前向传播和一次反向传播.轮次数量过少容易导致神经网络欠拟合,轮次过多容易导致神经网络过拟合.因此,训练轮次需要选择合适的值.
批次大小(batch_size):指的是每次送入神经网络的样本的数量.自2012年以来,其默认的策略是最大限度增大batch_size,直到“吃满”内存为止.其原因是:batch_size太小导致训练过程不容易收敛,而大的batch_size使得训练过程中的振动幅度减小,且容易收敛.但是,2018年,Masters和Luschi (2018)通过开展大量的实验指出过大的batch_size对测试集不利,即泛化能力较差.并指出最佳的实验表现都是在batch_size处于2~32之间.因此,其选择策略是:当有足够算力时,选取batch_size为32或更小一些;算力不够时,在效率和泛化性之间做折衷,尽量选择更小的batch_size(Masters and Luschi, 2018).
优化器:深度神经网络中的目标函数比较复杂且一般为自定义的损失函数,而神经网络的优化目标是求得损失结果最小条件下的网络参数状态,这种优化问题一般不存在解析解,通常需要使用数值计算的理论和技术更新网络参数,逼近最优解.将这种迭代更新求解网络参数的工具称为优化器.目前深度学习中有多种优化器可供选择,其中最基本的优化器是随机梯度下降法(Stochastic gradient descent, SGD),SGD虽然能达到极小值,但是其他用的时间长,而且可能会被困在鞍点.类似这种的传统优化器通常将学习率设置为常数或者根据训练次数调节学习率,从而极大地忽略了学习率其他变化的可能性,进而严重影响了模型的性能.而自适应性学习率优化器通过采取一些策略更新学习率提高模型的训练速度和模型性能,使得其广泛应用于深度学习中.常用的自适应优化器包括Adadelta(Zeiler, 2012),RMSprop(Root Mean Square Prop)(Graves et al., 2013)和Adam(Adaptive Moment Estimation)(Kingma and Ba, 2014)等.这些优化器均采用历史梯度信息调整学习率.
激活函数:在神经网络中用激活函数给神经网络加入一些非线性因素,使得网络可以更好地拟合复杂函数表达式.在深度神经网络中,常用的激活函数是:Sigmoid,tanh,Relu和Softmax函数.激活函数的选择通常按照下列规则:Softmax 常常是作为多分类神经网络的输出;Sigmoid函数常用于二分类,且适合浅层神经网络且需要配备较小的初始化权重(防止输入到激活函数的数值落入饱和区间);tanh函数具有中心对称性,适合于有对称性的二分类;在深度学神经网络中,ReLU函数被广泛应用.其主要原因是:ReLU不仅仅使得梯度的计算变快,而且能够缓解Sigmoid和tanh引起的梯度弥散和爆炸问题.
本文在复现SDNN网络的闪电哨声波智能检测模型时,其调参过程如表4所示,详细过程如下:
(1)学习率:设初始的参数组合(lr=0.1,optimizer=Adam,batch_size=64,activation=Relu,momentum=0.9,epoch=40).其loss曲线的变化如图30所示,观察前10个epoch的loss值在快速下降,从第10个轮次开始,loss值基本不再变化,因此,其最终的loss值是1.087.这说明初始的学习率太大,且从第10个轮次开始神经网络几乎停止“学习”.此时,继续按照下列方式调整学习率:保持其他参数不变,将学习率减少到lr=0.01,得到如图31所示的loss曲线,其中每个epoch的loss值均低于图30的loss值,且从第10个epoch开始,loss值具有持续变化的趋势,最终的loss值是1.051;继续向下调整lr=0.001,得到如图32所示的loss曲线:发现整个训练过程中的loss值不仅仅下降速度快,而且随着训练轮次的增加,loss变化的趋势也比较明显,说明随着训练轮次的增加,神经网络依然在“学习”,其最终的loss值是0.157.继续调整lr=0.0001得到如图33所示的loss曲线,此时发现其loss值下降速度快,神经网络的”学习“趋势依然存在,最终的loss值是0.384,将其与图32进行比较发现:图33所示的loss曲线整体明显高于图32所示的loss曲线,说明图32所代表的神经网络的性能优于图33所代表的神经网络的性能.此时,停止参数调整,将图32对应的学习率设为SDNN网络的初始学习率,即lr=0.001.

图30 初始学习率0.1,轮次40Fig.30 Learning Rate=0.1 and epoch=40
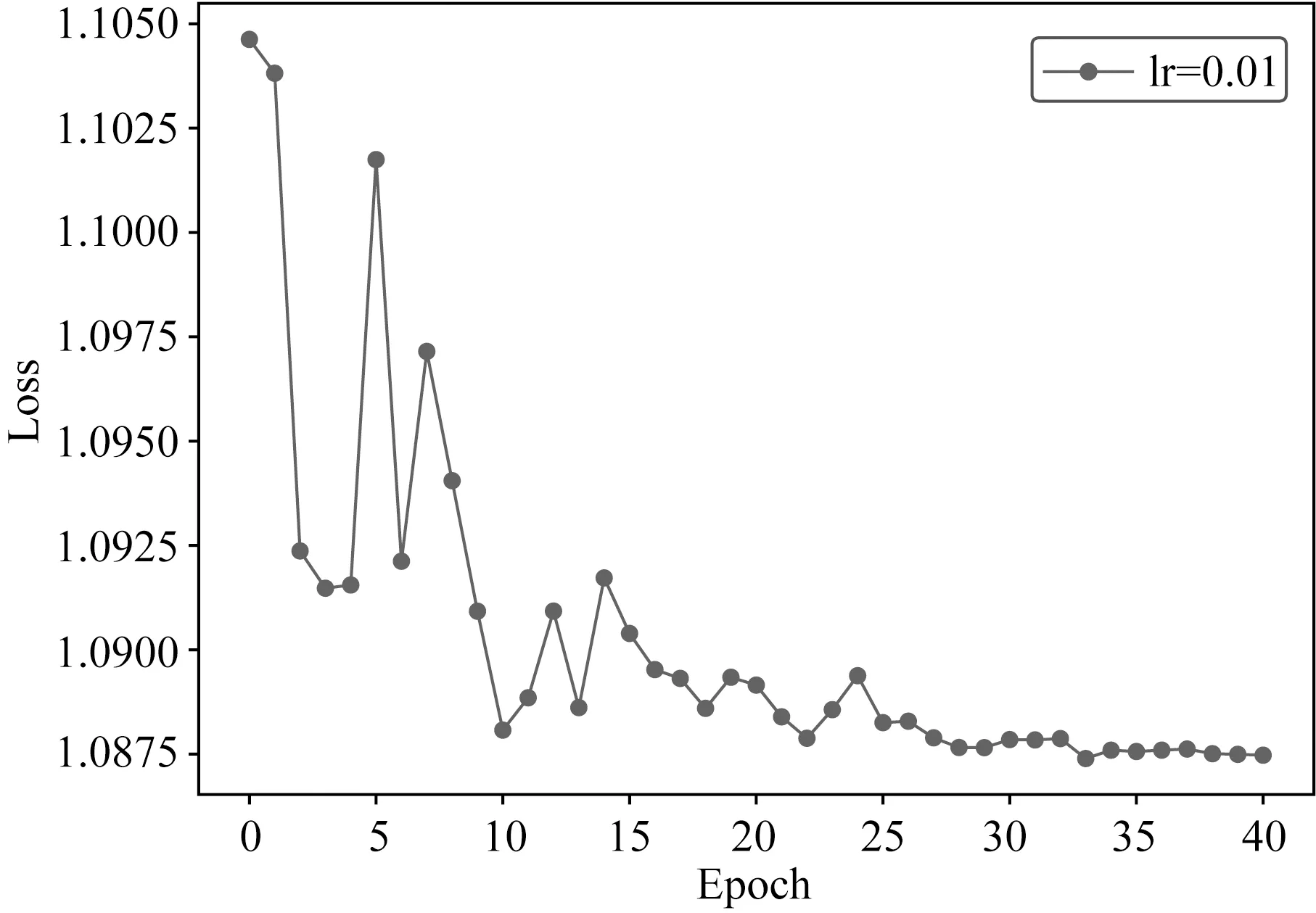
图31 初始学习率0.01,轮次40Fig.31 Learning Rate=0.01 and epoch=40

图32 初始学习率0.001,轮次40Fig.32 Learning Rate=0.001 and epoch=40
(2)轮次:目前最优的超参数是图32代表的参数组合(lr=0.001,optimizer=Adam,batch_size=64,activation=Relu,momentum=0.9,epoch=40),其最终的loss值是0.157.继续观察图32所示的loss曲线:发现在epoch=40的地方,loss依旧呈现下降趋势,此时的参数调整策略如下:继续增大epoch到70,得到图34所示的loss曲线,其最终的loss值是0.0603,而且在epoch=70的附近,loss的变化趋势已经逐渐平稳,说明此时的神经网络已经停止了学习.因此,参数epoch的值无需再继续增加,停止对该参数进行调整,设置SDNN网络的epoch为70.
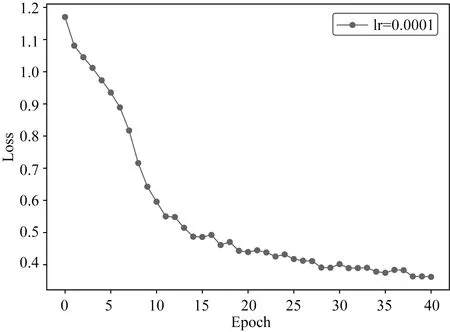
图33 初始学习率0.0001,轮次40Fig.33 Learning Rate=0.0001 and epoch=40
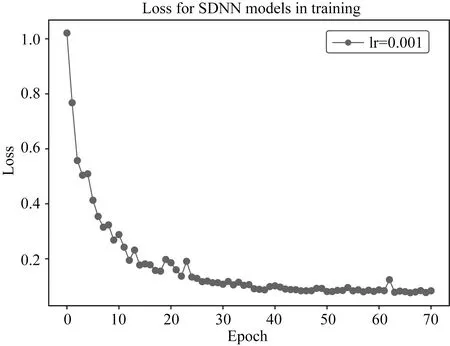
图34 初始学习率0.001,轮次70Fig.34 The learning rate=0.001 and epoch=70
(3)批次大小:在参数组合(lr=0.001,optimizer=Adam,batch_size=64,activation=Relu,momentum=0.9,epoch=70)的基础上,为了得到最佳的batch_size,尝试对其进行调整:如表4所示,保持其他参数不变,适当增大batch_size到128,发现其最终的loss值是0.0714;继续增加batch_size到256,发现最终的loss值变为0.0742;此时意味着大的batch_size导致其loss变差,则尝试batch_size=32,发现其最终的loss值变为0.0089;持续减少batch_size到16,发现其loss值较0.0089变大,为0.0187,此时,停止参数调整,选择最低的loss值对应的批次大小为SDNN网络的batch_size的值,即batch_size=32.
(4)优化器:在参数组合(lr=0.001,optimizer=Adam,batch_size=32,activation=Relu,momentum=0.9,epoch=70)的基础上,保持其他参数不变,将优化器分别设置为:Adam,Adadelata和RMSprop,计算其最终的loss值,如表4所示,分别是0.0089,0.8011,0.9742.选择最低的loss值所对应的优化器为SDNN网络的优化器参数,即optimizer=Adam.
(5)激活函数:在参数组合(lr=0.001,optimizer=Adam,batch_size=32,activation=Relu,momentum=0.9,epoch=70)的基础上,得到最终的loss值是0.0089.再将激活函数分别调整为tanh,Softmax,Sigmoid后进行模型训练,得到最终的loss值,如表4所示,分别是1.703,1.847,1.912.选择最低的loss值(0.0089)所对应的激活函数为SDNN网络的激活函数,即activation=Relu.

表4 SDNN网络的调参过程Table 4 Parameter adjustment of the SDNN model
按照类似的过程调试YOLOV3网络的参数,如表5所示.得到SDNN网络和YOLOV3网络的最佳参数如表6所示.这说明按照上述的调参策略得到的超参数组合,能够使得网络参数在更新过程中获得比较合适的方向和步长,达到学习的目的,并最终获得较优的网络参数.
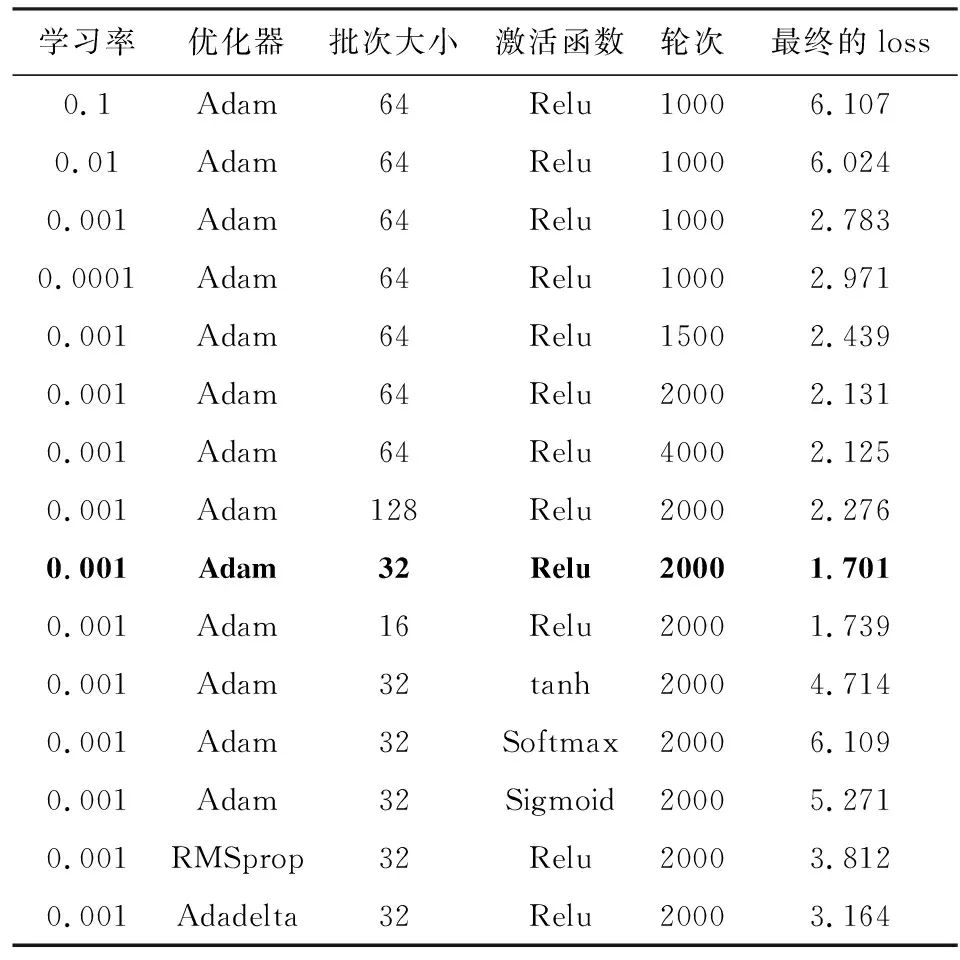
表5 YOLOV3网络的调参过程Table 5 Parameters adjustment of the YOLOV3 model

表6 SDNN网络和YOLOV3网络最终的参数设置Table 6 Final parameter settings of SDNN network and YOLOV3 network
4.3 代表性算法的模型训练过程
基于形态学的闪电哨声波智能检测算法的模型,无训练过程,无训练时间成本.
基于SDNN网络的闪电哨声波智能检测算法的模型主要有3层卷积神经网络构成,其超参数的设置如表6所示.该模型的训练环境:Windows10 64位系统,使用Nvidia GeForce RTX2080Ti显卡,CUDA10.0和cuDNN调用GPU加速训练,模型的训练过程如图35a所示:在前10个epoch内,其损失值急剧衰减,到第65个epoch后训练过程基本处于稳定,训练时间是0.16 h.
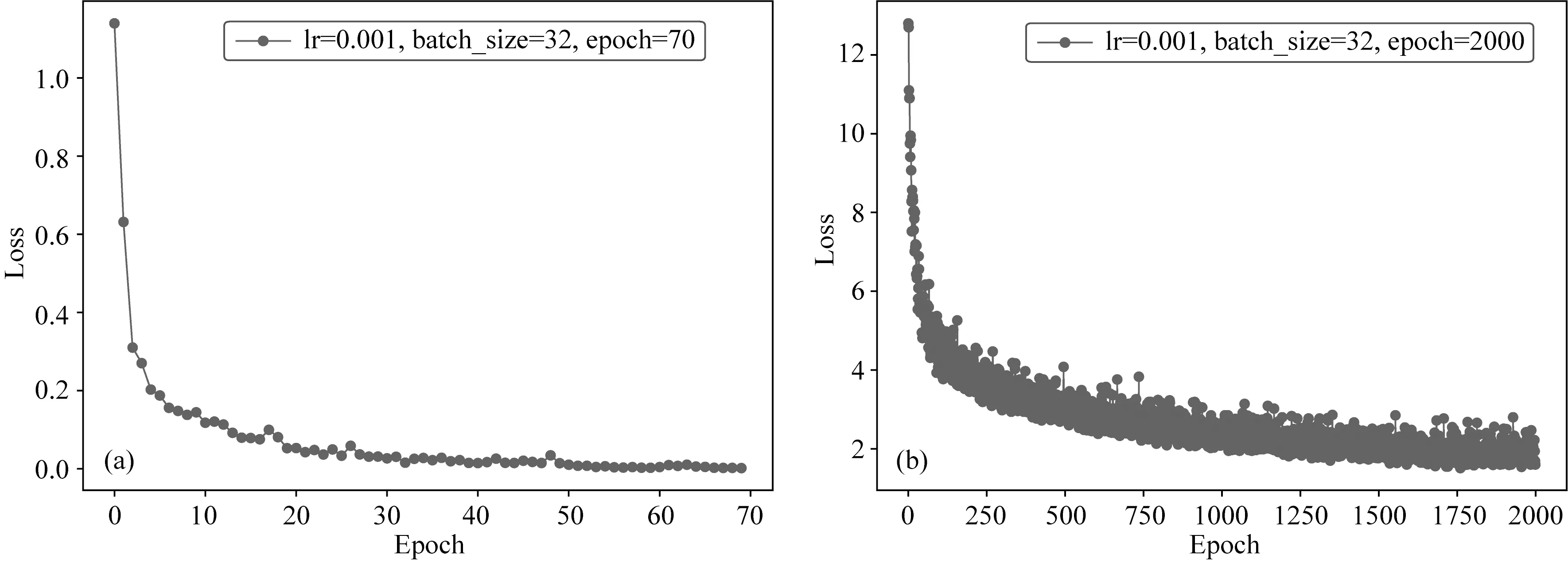
图35 神经网络的训练过程(a) SDNN网络; (b) YOLOV3网络.Fig.35 Training the neural networks(a) SDNN; (b) YOLOV3.
基于YOLOV3网络的闪电哨声波智能检测算法的模型主要有252层的神经网络构成,其超参数的设置如表6所示,该模型的训练环境与SDNN网络的环境相同,其模型的训练过程如图35b所示:在前500epoch内,其损失值急剧衰减,直到第1800个epoch后损失值基本处于稳定,其训练时间是4.5 h.
其中,神经网络的训练时间成本主要受三方面影响:硬件设施,模型复杂度和超参数中的优化器.
在硬件设施相同的情况下,模型越复杂、网络层数越多,参数越多,其计算量就越大,同时其超参数“轮次”的值越高,因此,导致其训练的时间越长.比如SDNN网络由三层卷积网络构成,其最佳的epoch为70,训练时间是0.16 h;而YOLOV3神经网络由252层网络构成,其最佳的epoch为2000,训练时间是4.5 h.
在网络优化的过程中,训练时间成本主要与优化器的选择有关.最基本的优化器是SGD,但是SGD的优化速度较慢,容易驻留在鞍点.为了提高训练速度和性能,大量的实验表明通过设置一个根据迭代次数衰减的学习率具有明显效果.其基本思想是:在训练前期调整学习率的值变大,训练后期调整其变小.常用的学习率衰减策略包括分段常数衰减,指数衰减,自然指数衰减,余弦衰减等.但对学习率超参数的初始设置具有较强的依赖,而自适应优化器主要利用历史梯度信息自适应调整学习率,降低了对初始学习率参数的依赖性,同时加快了优化速度.常用的自适应优化器是Adadelta,RMSProp和Adam.在实际应用中,需结合具体问题有针对性地选择合适的优化器.
4.4 代表性算法的复现效果
本小节主要从定量和定性的角度比较三种复现算法的效果:其中定量比较如表7所示,定性比较如图36—38所示.基于形态学处理的闪电哨声波智能检测算法对噪声敏感,虽然采用中值滤波、开运算等方式滤除了一部分干扰,如图36(c,d,e)所示,但仍然难以克服噪声对该算法产生的影响,如图36f显示的是连通域的标记结果,其中每个星号点是一个连通域的重心.对比图36a和图36f可知:图36f中的两个椭圆区域各有一条闪电哨声波,即理论上每个椭圆区域内应该各有一个连通区域且每个区域有一个星号点所表示的连通域的重心.仔细观察图36f中的两个椭圆区域发现:每个椭圆区域均存在多个星号点,说明每个椭圆区域存在多个连通域.说明连通特性被干扰点破坏,使得一个完整的哨声波区域被标记成了若干个连通区域,导致连通域分析出现了较大的偏差,最终使得这两条闪电哨声波被漏检.因此,该方法的漏检率较高.而滑动卷积神经网络(SDNN)通过特征学习获得了较鲁棒的哨声波特征,并有效地克服了上述噪声的干扰,但由于采用了固定大小的滑动窗,导致图37最下边的闪电哨声波(椭圆标记区域)被漏检了.YOLOV3网络由于将自动特征提取、分类和定位统一整合在其损失函数所表示的数学模型中,其在定位方面比滑动卷积神经网络更精准,如图38所示,但模型的训练时间长.总之,人工定义的特征不具有鲁棒性容易受到噪声等因素的干扰,自动化提取的特征较之更为鲁棒,且自动定位效果亦更为精准.

表7 三种闪电哨声波自动检测算法在张衡一号卫星数据中的效果Table 7 Results of three different methods for detecting lightning whistler from the data captured by ZH-1 satellite

图36 基于形态学处理的闪电哨声波检测算法(a) 原始时频图; (b) 灰度化; (c) 二值化; (d) 中值滤波; (e) 开运算; (f) 连通域分析/连通域标记; (g) 连通域筛选; (h) 最终结果.Fig.36 The Process of lightning whistler detection algorithm based on morphological processing(a) Original time-frequency diagram; (b) Gray image; (c) Binarization; (d) Median filtering; (e) Open operation; (f) Connected domain analysis/connected domain labeling; (g) Connected domain filtering; (h) Final result.

图37 滑动卷积神经网络的检测的效果Fig.37 SDNN neural network
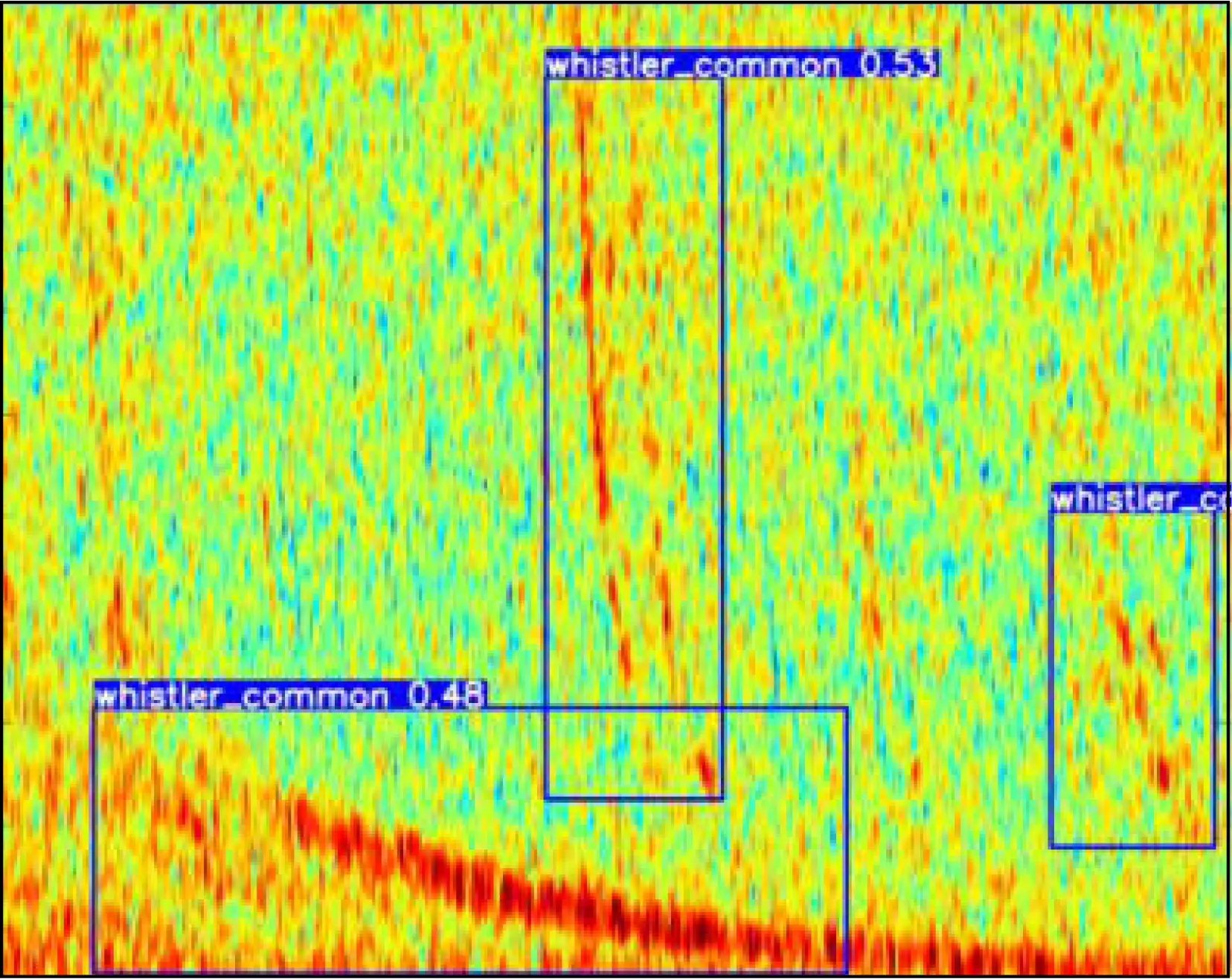
图38 YOLOV3神经网络的检测的效果Fig.38 YOLOV3 neural network
5 总结与展望
近年来,电磁卫星的监测数据量急剧增长,闪电哨声波智能检测作为人工智能与地球物理交叉的研究方向,受到了广泛关注.本文对基于电磁卫星数据的闪电哨声波智能检测进行了全面而层次化的综述.通过综述可以得到以下结论:
(1)电磁卫星:目前电磁卫星的闪电哨声波的研究主要集中在DEMETER卫星、Arase 卫星和Akebono卫星,其目的是统计闪电哨声波全球的分布特点,并通过卫星的闪电哨声波反演电离层的高通电子量、等离子密度等信息.
(2)闪电哨声波智能检测方法在时频图的基础上,借鉴计算机视觉和机器学习的相关技术,通过逐步实现特征提取、分类和定位等过程达到了自动检测闪电哨声波的目的.表8—10分别从特征提取、分类和定位三个方面对闪电哨声波智能检测算法进行了总结整理和对比.
表8总结和对比了闪电哨声波智能检测算法中的特征提取技术:①人工提取特征(The Stanford VLF Group, 2018; Fiser et al., 2010; Ali Ahmad et al., 2019; Dharma et al., 2014; Oike et al., 2014):该方法是依赖人工观察闪电哨声波的时频图,结合闪电哨声波的物理机理总结出闪电哨声波的特征,比如色散形状等,然后采用数字图像处理技术设计预处理算法以增强该特征,最后再采用计算机视觉技术设计算法提取该特征.这种方式适合在数据量不大的情况下进行使用,且时间成本低.但闪电哨声波的色散形状亦是多种多样,采用计算机视觉相关技术提取的人工定义的特征仅仅能够代表一部分闪电哨声波的特征,该特征不仅仅泛化性差且容易受到噪声的干扰.说明人工提取的特征鲁棒性差,在数据量大的情况下其检测效果不佳.②自动提取特征(Konan et al., 2020):首先在时频图上,由人工标注大量的单闪电源的单条频谱线的闪电哨声波,然后将这些标注图片数据输入到神经网络去训练得到一模型,该模型能够自动提取闪电哨声波特征.这种方式可以获得较鲁棒的闪电哨声波特征,在数据量增大的情况下,其检测到的单闪电源的单谱线的闪电哨声波的效果最佳.

表8 闪电哨声波智能检测算法中的哨声波特征提取方法的总结和对比Table 8 Summary of the feature extracting methods in the lightning whistler detection algorithms
表9总结和对比了闪电哨声波智能检测算法中的分类技术:①模板匹配(The Stanford VLF Group, 2018; Fiser et al., 2010; Ali Ahmad et al., 2019; Dharma et al., 2014; Oike et al., 2014):该方法首先依赖人工提取闪电哨声波的特征,对其进行归一化处理后得到闪电哨声波的特征模板,然后提取待识别的闪电哨声波的特征,将该特征与特征模板进行匹配,匹配度高意味着该图像是闪电哨声波,否则认为该图像是非闪电哨声波图像.该方法存在两方面的局限性:第一个局限性来自于模板,闪电哨声波虽然具有色散状特征,但该特征有大量的不同的形态.因此,难以用一个标准化模板表示所有的闪电哨声波的色散特征.第二个局限性来自于匹配,匹配策略可被视作一线性分类器,随着闪电哨声波数据量的增加以及色散特征的多样化,线性可分性越来越难以满足,导致分类结果变差.②神经网络分类器(Konan et al., 2020):神经网络能够很好地拟合闪电哨声波图像与识别结果之间的非线性关系,并克服线性分类器的缺点,总之,神经网络分类器分类效果优于模板匹配分类器.

表9 闪电哨声波智能检测算法中的哨声波分类(识别)方法的总结和对比Table 9 Summary of the classification methods in the lightning whistler detection algorithms
表10总结和对比了闪电哨声波智能检测算法中的定位技术:①滑动窗定位(The Stanford VLF Group, 2018; Fiser et al., 2010; Ali Ahmad et al., 2019; Dharma et al., 2014; Oike et al., 2014; Konan et al., 2020):在时频图上,固定一个大小的时间窗,比如以步长2 s进行滑动,对每一个滑动区域进行特征提取和分类(识别),该方法简单易实现但最大的问题是闪电哨声波持续的时间是不固定的,其时间尺度范围从毫秒级到秒级,因此,滑动窗定位的方式只能定位出某个固定时间宽度的闪电哨声波,定位精度低.②智能判断定位(Konan et al., 2020):采用YOLOV3神经网络对闪电哨声波图像区域与其相邻的上下文图像区域进行建模,经过大量的训练后得到的神经网络模型能够准确地定位到任意时间宽度的闪电哨声波.

表10 闪电哨声波智能检测算法中的哨声波定位方法的总结和对比Table 10 Summary of the location methods in the lightning whistler detection algorithms
总之,闪电哨声波智能检测的研究处于起步阶段.目前的闪电哨声波智能检测算法仅在识别单条的闪电哨声波方面取得一定的效果.通过综述分析目前的电磁卫星的闪电哨声波智能检测算法,本文认为该领域未来的发展趋势和应用前景将主要体现在以下四个方面.
(1)现有的智能检测算法能够检测出大部分的单个闪电源的单条频谱线的闪电哨声波类型,如何检测出表1中由单个闪电源的多条频谱线组成的闪电哨声波是探索空间物理现象机制亟需解决的问题.针对多条频谱线的闪电哨声波类型,其典型的特点是由多条色散状的频谱线组成,衰减速度随着时间的变化逐渐变小,同时频谱强度逐渐减少.可在单条频谱线的哨声波检测的基础上,通过计算机视觉处理技术提取频谱曲线的斜率变化,用其表达该曲线的衰减信息,将提取得到斜率和频谱强度随时间变化的信息作为时间序列,进一步设计循环神经网络以实现对单闪电源的多条频谱线的闪电哨声波进行智能检测的功能.
(2)单条频谱线的闪电哨声波依然存在多种形态,在闪电哨声波智能检测结果的基础上,能够根据用户提供的闪电哨声波图像自动地从海量的电磁卫星的数据池里找到与其形态相似的若干张哨声波图像并返回相关的时空信息,是未来研究的方向之一.其方案如图39所示:首先通过对电磁卫星的数据进行预处理和傅里叶变换等方式建立电磁卫星数据池;然后,输入待查询的闪电哨声波图像,提取待查询的闪电哨声波图像的形状特征、位置信息、频谱强度特征以及斜率特征等创建待检索向量;然后借用哈希技术对待检索向量进行哈希编码;接下来,在电磁卫星数据池中采用闪电哨声波智能检测算法检测识别单条频谱线的闪电哨声波,再对每个检测到的闪电哨声波采用计算机视觉等技术提取其形状特征、位置信息、频谱强度特征以及斜率特征等信息,利用这些信息创建向量表示该闪电哨声波,同时对该向量进行哈希编码.计算待检索数据的哈希编码与数据池中每个数据向量的哈希编码之间的汉明距离,选择前K(K是非负整数)个最小的汉明距离所对应的闪电哨声波图像即为检索到的闪电哨声波图像,且检索到的图像共有K张.
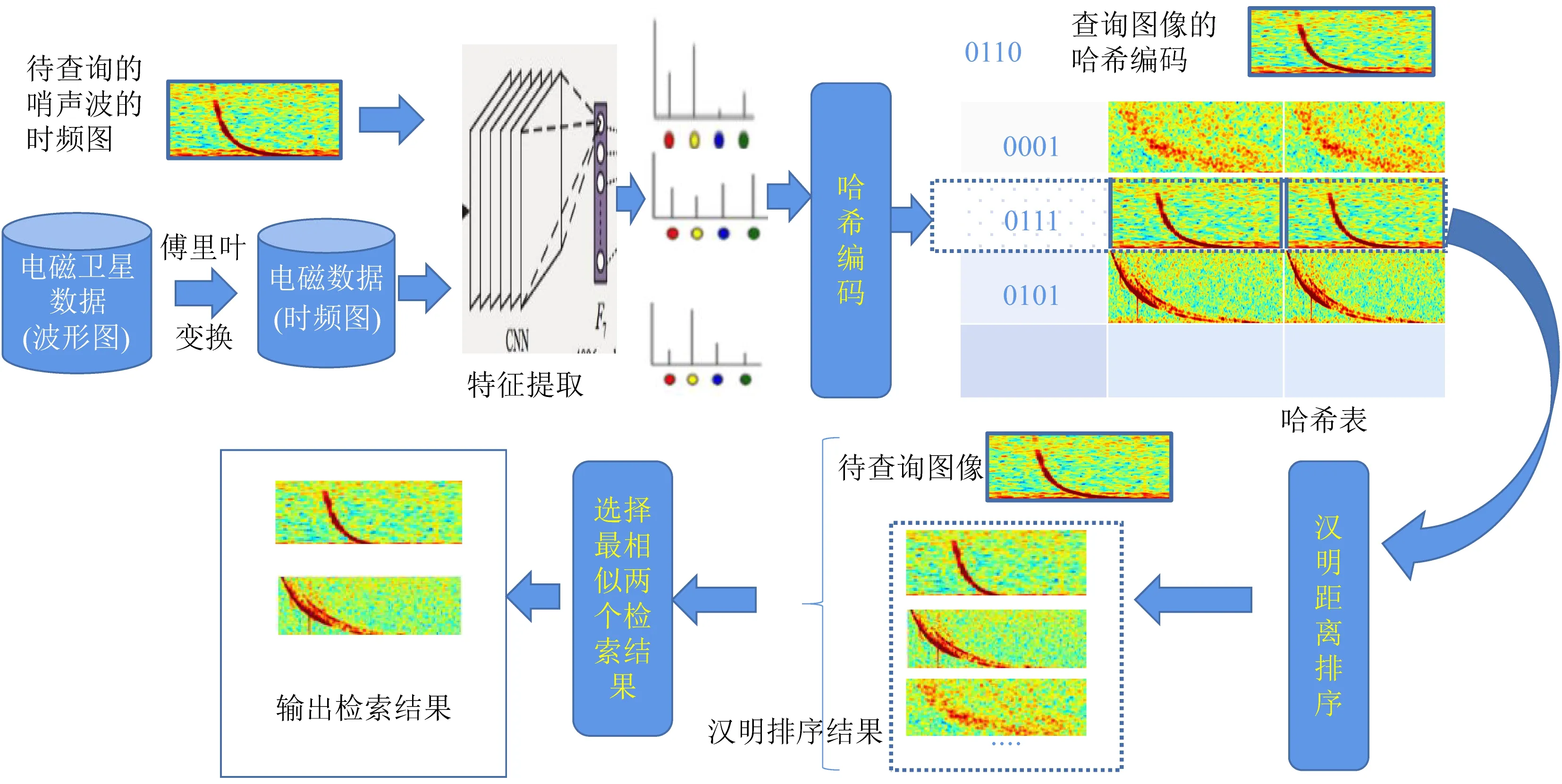
图39 基于哈希的哨声波图像智能检索Fig.39 The image retrieval technology of lightning whistler based on Hashing
(3)目前的闪电哨声波检测算法没有公开的庞大的数据库,构造闪电哨声波电磁卫星的数据库亦是目前亟需解决的问题,可通过收集ZH-1卫星VLF波段感应磁力仪数据和电场探测仪数据,将其转化成时频图后,通过人工处理方式建立统一的电磁卫星的闪电哨声波数据库,以期大力推动闪电哨声波智能检测算法的发展.
(4)目前的闪电哨声波智能检测算法能够检测出部分闪电哨声波,在此基础上,根据其形态特征开展哨声波的轨迹跟踪是进行电子密度估计的关键,值得研究和探索.可通过跟踪其轨迹,利用轨迹的幅值和色散度反演电子密度.
致谢本工作使用了中国国家航天局和中国地震局支持的张衡一号卫星的观测数据.特别感谢来自应急管理部国家自然灾害防治研究院张衡一号卫星团队的所有成员为本文研究数据提供的技术服务支持.
