单极源钻铤波传播机制的实验研究2
2021-05-07王军聂成洋侯许佳关威张超
王军, 聂成洋, 侯许佳, 关威 , 张超
哈尔滨工业大学航天学院, 哈尔滨 150001
0 引言
随钻声波测井是当前主流的储层评价方法之一(Aron et al.,1994),更因其在油气勘探方面的独特优势,自问世以来就备受石油工业界青睐.为了充分认识随钻声波测井技术的特点,提高测井数据的解释能力,前人针对随钻声波测井的波场特性及钻铤波的传播规律展开了相关研究工作.Wang和Tang(2003)使用时域有限差分方法模拟了软地层中偶极和四极声源激发的井孔声场.崔志文(2004)针对弹性和孔隙地层中随钻声波测井响应进行了理论和数值研究.Sinha 等(2009)比较了多极子钻铤波的激发强度和频散规律.王瑞甲和乔文孝(2015)计算了随钻四极子声波测井中地层各向异性参数与钻铤波的关系.苏远大等(2011,2015)通过分析钻铤波的激发和衰减规律,提出了利用声阻带来抑制钻铤波传播的想法.朱祖杨等(2016)采用有限差分研究了钻铤结构对随钻声波测井中钻铤波的影响.Wang等 (2016)和杨玉峰等(2016)分析了不同模型激发钻铤波的传播特性,Yang等(2017)又进一步分析了钻铤内外刻槽尺寸对钻铤波幅值的影响.Ji等(2019)研究了钻铤波峰值随径向位置和频率的变化关系.谭宝海等(2018)通过改变激励信号的周期数,来调节钻铤波的激发频带,使其置于隔声体的阻带内以削弱钻铤波.王军等(2016)在实验室内记录了砂岩和有机玻璃模型中多极源随钻声波测井的全波波形,又观测了不同模型下单极源钻铤波的传播规律(王军等,2019),并与理论预测结果(杨玉峰等,2016;Yang et al.,2017)进行对比,两者吻合较好.
上述工作的开展极大地推动了随钻声波测井技术的进步,然而钻铤波干扰地层波测量的问题至今仍未解决,特别是针对地层纵波速度的测量成为该技术难点,因为地层横波可通过偶极或四极随钻测井两种手段获取,且四极螺旋波几乎不受钻铤波的影响(Tang et al.,2006;Zhu et al.,2008;王军等,2016).因此,如何准确测量地层纵波速度是随钻测井技术亟待解决的问题.已有研究表明:基于孔隙介质动电效应的随钻动电测井技术可有效抑制钻铤波对地层波的影响,从而能够预测地层纵横波速度(Guan et al.,2013;郑晓波等,2014;丁浩然等,2016) ,并获得了室内随钻动电测井实验数据的有效验证(王军等,2017,2020),肯定了随钻动电测井技术的可行性和应用前景.但由于随钻动电测井技术尚处于研究阶段,目前还无法进行现场勘探测量.鉴于纵波速度对地层参数评价的重要性,能否在现有随钻声波测井技术的基础上,提出纵波速度的测量解释新方法成为当前测井领域的热点和难点问题.
随着研究的不断深入,学者们发现钻铤波是一种导波,它不仅在钻铤内部传播,同时还要向钻铤外部辐射能量,进而在井内流体和地层中传播(Guan et al.,2013;郑晓波等,2014;Wang et al.,2016;杨玉峰等,2016;Yang et al.,2017;He et al.,2017).王军等(2020)将钻铤内、外传播的钻铤波分别命名为“内钻挺波”和“外钻铤波”,以区分这两个不同区域内传播的钻铤波.本文则针对内、外钻铤波的频率响应特性,以及地层纵波的随钻测量问题,在无限大流体和井孔模型条件下,开展了单极源随钻声波测井实验研究,记录了不同激发频率下单极源钻铤波的时域波形,进而分析了内钻铤波和外钻铤波随频率的变化规律.之后基于随钻声波测井原理和内外钻铤波的能量分布规律,提出一种地层纵波速度的提取方法,并通过缩小的模型井中随钻声波测井实验测量验证了方法的可行性.
1 随钻测井探头及实验模型
我们曾在前期工作中设计了缩小尺寸的随钻测井探头(王军等,2019),其中声源由4个均匀分布的薄圆柱状压电片构成,6组声波接收器由同样材质的压电片嵌于钻铤内部构成(见图1a).考虑到我们依旧采用上述探头进行实验研究,这里不再详细介绍探头的结构设计.本文在两种模型下进行了随钻声波测量实验.由于实验过程中探头距离水槽(120 cm×80 cm×60 cm)的最小距离约为30 cm,该距离远大于钻铤直径(2.5 cm),因此在实验过程中水槽壁的反射波对内外钻铤波的影响可忽略,进而认为图1b模型为无限大流体模型.图1b用于分析内/外钻铤波的传播特性.其中内嵌的PZT传感器记录沿着钻铤传播的内钻铤波信号,8103水听器记录钻铤外部流体中的外钻铤波信号.图1c为随钻声波测井模型,用于地层纵波速度测量的方法研究.实验用流体为自来水,井孔为缩小尺寸的砂岩模型井,直径3 cm,约为实际井孔直径的十分之一,其纵横波速度(3900 m·s-1和2200 m·s-1)和渗透率(15×10-15m2)是对岩样取心后测量得到.

图1 随钻测井探头及实验模型(a) 随钻测井探头; (b) 无限大流体模型; (c) 随钻声波测井模型.Fig.1 The detector of acoustic logging while drilling and the experimental models(a) The acoustic LWD detector; (b) The infinite fluid model; (c) Acoustic LWD borehole model.
实验测量系统如图2所示,主要设备包括函数信号发生器(AFG3020B)、高压脉冲源(奥林巴斯5077PR)、前置放大器(5660C)、滤波器(NF3628)、NI数字信号采集装置(Pxie-1082).表1简要介绍上述仪器的主要作用和参数设置.

表1 实验仪器以及主要功能Table 1 The experimental devices and their functions

图2 实验测量流程图Fig.2 The diagram of experimental system
2 单极源钻铤波频率响应特性分析
由随钻声波测井原理可知,接收器记录的测井全波主要包括两大类信号(见图3),第一类是携带地层有效信息的地层波(纵波、横波、斯通利波等);第二类是干扰地层波测量的钻铤波(2号标记的外钻铤波和3号标记的内钻铤波).由于传统电缆测井技术对井孔地层波特性的研究已经非常成熟,因此,在随钻声波测井情况下深入了解钻铤波的传播机制是非常有必要的.我们在前期工作中分析了内、外钻铤波沿着轴向和径向的衰减规律(王军等,2019),但文中未研究钻铤波的频率响应特性.故针对内、外钻铤波频响特性的实验研究是本文主要工作之一.
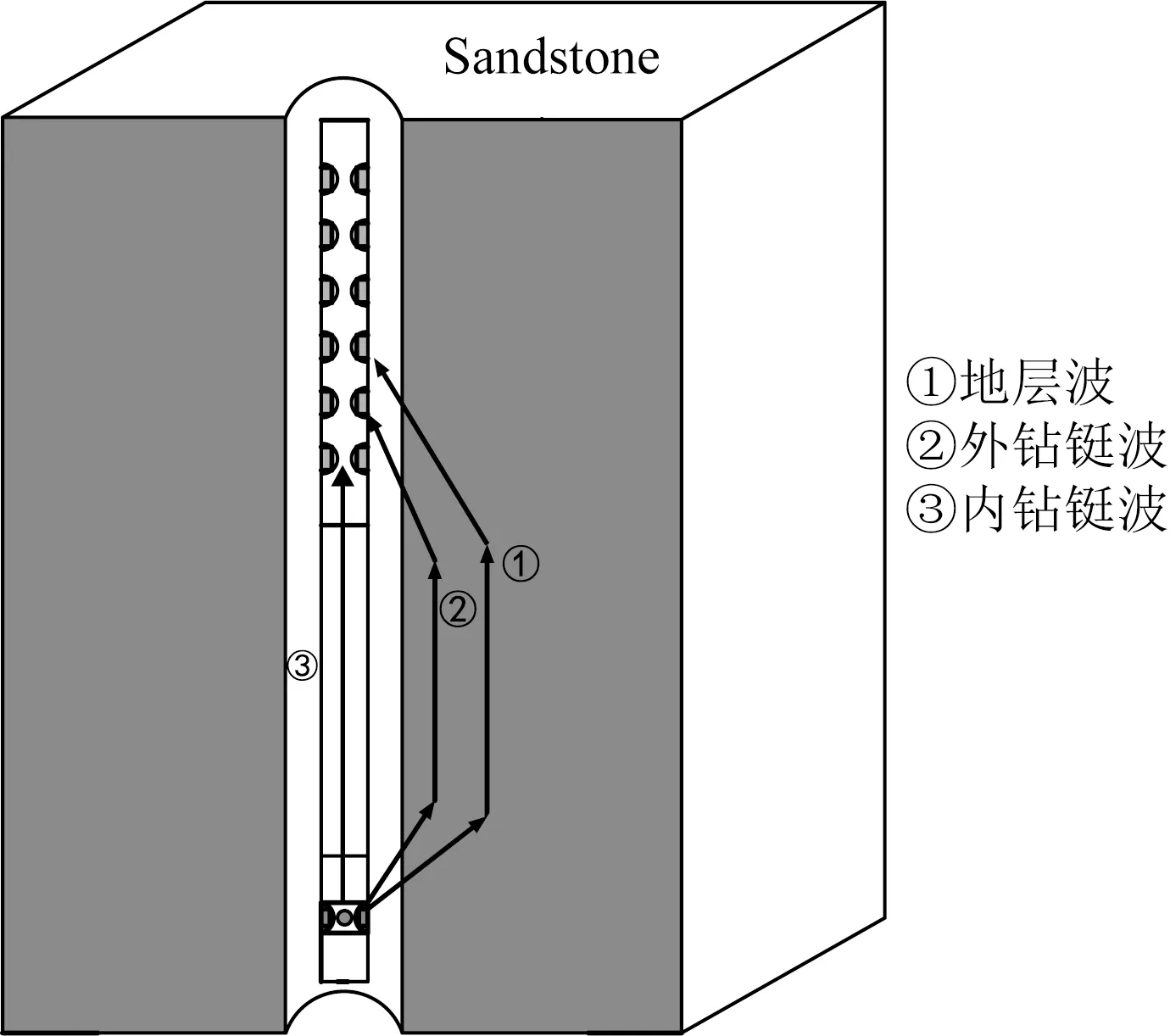
图3 随钻声波测井信号分类图Fig.3 The recorded acoustic signals in LWD measurements
依据图1b所示无限大流体模型,我们采用王军等(2019)测量方法,利用钻铤内部PZT压电片记录内钻铤波信号(图4),之后利用BK8103水听器在钻铤外表面记录外钻铤波信号(图5).由于没有井壁反射界面的存在,实验记录内、外钻铤波信号之间没有耦合叠加关系,从而可将内、外钻铤波相互分离开来,以便独立分析两者的频率响应特性.
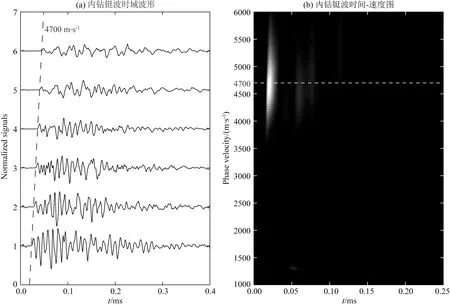
图4 内钻铤波时域波形图及时间速度图Fig.4 The time domain waveforms of inner collar wave and its semblance
图4为高压脉冲源激励下,6个PZT压电片记录信号的时域波形及其对应的时间速度图.由实验测量过程可知,时域波形中最先被记录到的信号为内钻铤波信号,其传播速度可通过6条曲线到时连线的斜率计算得出(4700 m·s-1),该结果与时间速度图中显示的钻铤波速度一致.图5为BK8103水听器记录的外钻铤波信号.实验过程中,水听器紧贴在钻铤的外表面,起始位置与第一个内嵌压电片的位置一致,之后利用三轴定位仪准确控制水听器的运动轨迹,每次移动2 cm,保证水听器与内嵌压电片处于相同的源距位置.与图4中只有内钻铤波信号不同,8103水听器记录到两个明显的波群,分别是波速4700 m·s-1的外钻铤波和1500 m·s-1的流体声波或外斯通利波信号.上述结果为后续内、外钻铤波的频率响应实验分析提供参考.此外,分析钻铤波的特性是我们的研究目标,所以本文中不研究钻铤波后面信号的传播规律.

图5 外钻铤波时域波形图及时间速度图Fig.5 The time domain waveforms of outer collar wave and its semblance
2.1 内钻铤波的频率响应特性
由于高压脉冲源只能提供尖脉冲方波信号,无法调节声源的激励频率.因此,为了细致地分析内钻铤波随频率的变化规律,实验改用单频正弦脉冲信号对声源进行激励.我们以第4个压电片为目标,记录了不同声源频率作用下(30~250 kHz)的内钻铤波信号.图6a为归一化处理后的时域波形图,其中第一条曲线表示声源激励频率为30 kHz时接收器记录的信号,之后声源频率依次递增10 kHz重复上述实验,直到声源频率达到250 kHz,共记录23条曲线.基于方波脉冲和正弦波脉冲频谱的差异性,图4和图6a中信号的波形形态有所不同,这不影响我们对实验结果的分析.
由图6a可以看出,最先达到的内钻铤波信号随着声源频率的提高,呈现出先增大后减小的趋势.当声源频率较低时(30~50 kHz),内钻铤波信号十分微弱.理论模拟计算发现,钻铤波在低频的激发强度也是最低的(Sinha et al.,2009),与本文实验数据所体现规律一致.不过需说明的是上述结果可能还与声源换能器自身的响应有关,因为现有工艺条件下,压电片的响应频带普遍较高,因此,在低频条件下,压电片不能正常激发能量,从而降低了钻铤波的激发强度.不过随着激发频率的提高,压电片正常工作,内钻铤波的幅值也逐渐增强.为了有效分析内钻铤波随频率的变化规律,我们从图6a时域波形中提取了内钻铤波信号的峰峰值,并绘出图6b所示归一化的频率-幅度图.从图中可以明显地看出,随着声源激发频率的提高,内钻铤波的幅值先快速增强(30~70 kHz),之后在70~120 kHz范围内基本保持不变,幅度达到最大值,然后又呈阶梯状缓慢下降的趋势(120~250 kHz).另外,从图6b中还可观察到:峰值左侧上升阶段的曲线近似为一条直线,随着频率增大上升较快.而峰值右侧下降段的曲线,呈现出阶梯状分段下降的规律,分别在120~150 kHz和170~200 kHz范围内出现了平段现象.接下来我们在相同条件下进行了外钻铤波的实验测量工作.
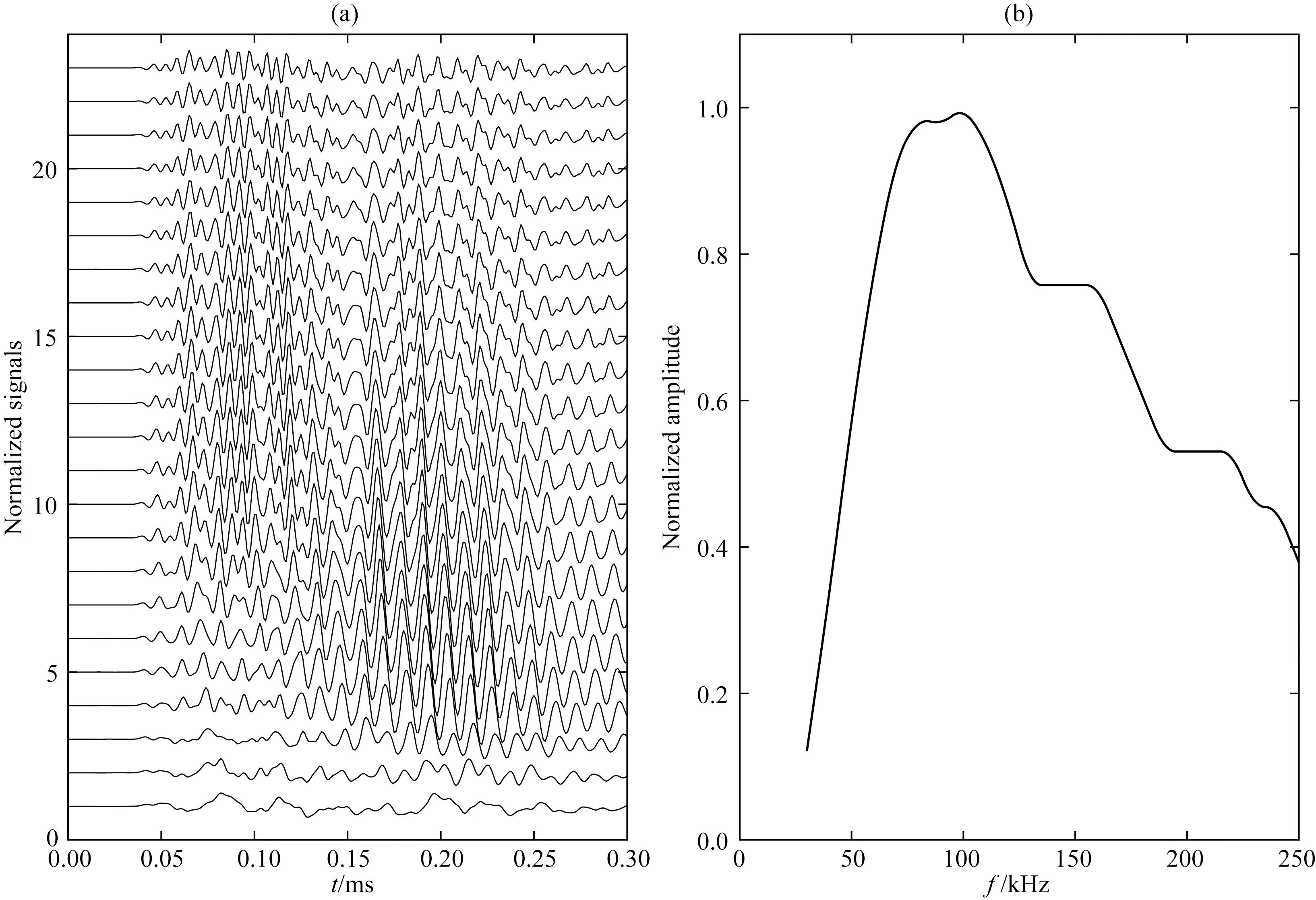
图6 内钻铤波幅值随激发频率的变化规律(a) 不同激发频率下内钻铤波时域波形图; (b) 内钻铤波幅值随激发频率变化曲线.Fig.6 The relationship between the amplitude of inner collar wave and the excitation frequency(a) The time domain waveforms of inner collar wave at different excitation frequency; (b) The variation curve of normalized amplitude of inner collar wave with excitation frequency.
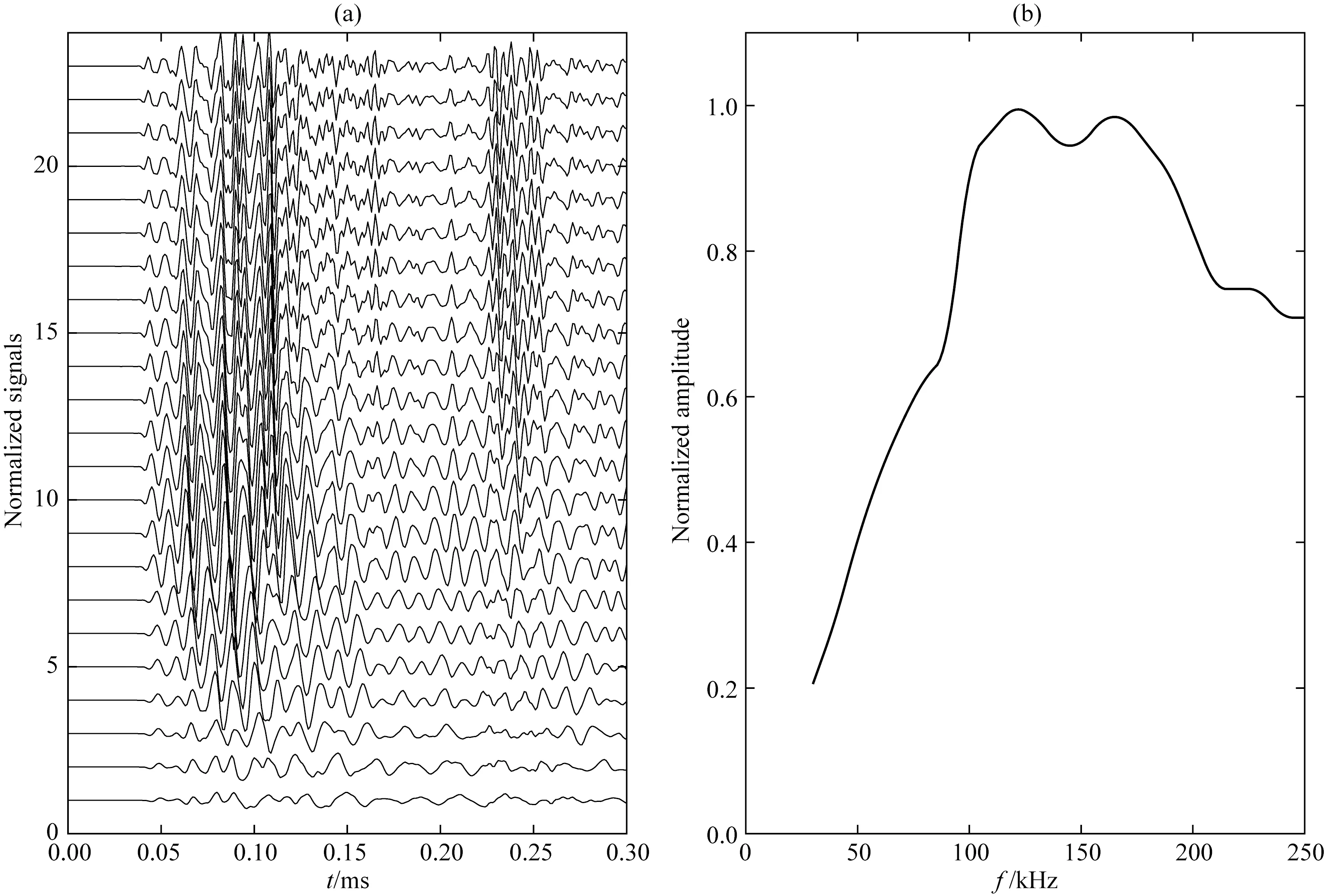
图7 外钻铤波幅值随激发频率的变化规律(a) 不同激发频率下外钻铤波时域波形; (b) 外钻铤波幅值随激发频率变化曲线.Fig.7 The relationship between the amplitude of outer collar wave and the excitation frequency(a) The time domain waveforms of outer collar wave at different excitation frequency; (b) The variation curve of normalized amplitude of outer collar wave with excitation frequency.
2.2 外钻铤波的频率响应特性
图7给出了声源频率在30~250 kHz范围内,8103水听器记录的时域波形(图7a)和外钻铤波幅值-频率曲线图(图7b).从图中可以看出,外钻铤波信号随频率的变化规律与图6结果非常类似:图7a时域波形中外钻铤波幅值先增大后减小;图7b幅值-频率曲线也呈现3个主要变化阶段:30~100 kHz范围内的快速上升阶段;之后是100~180 kHz范围内的基本不变阶段,最后是180~250 kHz范围内的下降阶段.由于内、外钻铤波本质上是一个导波,只是两者的传播区域不同而已,因此它们随频率变化规律类似是可信的.
不过我们也可从图6和图7中看出两者之间存在明显的不同,为了细致分析它们之间的差异性,我们将图6b和图7b重新绘制在图8a中,分别用实线和虚线表示.通过对比发现:
(1)两者在3个阶段对应的频率范围不同,如外钻铤波的峰值频带为100~180 kHz,比内钻铤波峰值频带(70~120 kHz)要宽许多,频率也更高一些.而且外钻铤波在峰值频带中的凹点(禁带现象)更明显一些.
(2)两者在上升阶段的变化率不同,通过计算得出外钻铤波幅值-频率曲线对应的两个斜率0.0084/kHz和0.0152/kHz,均小于内钻铤波曲线的斜率0.02/kHz.这说明内钻铤波在低频段对声源激发频率更加敏感.
(3)两者在下降阶段的变化形态不同,与内钻铤波相比,外钻铤波下降没有出现阶梯状形态,但两者的下降率接近.
上述结果可能是由于承载内、外钻铤波传播的波导材料不同引起的.因为承载内钻铤波的金属钻铤与承载外钻铤波的流体对声波的衰减影响不同.另外,王军等(2020)实验结果表明,钻铤波在向外辐射能量,形成外钻铤波的过程中会发生滤波的现象,即外钻铤波会缺失一定成分的频率分量,从而导致两者之间频率响应的差异性.
我们还进一步从理论方面计算了图1b无限大流体模型中,单极源钻铤波的激发强度曲线,该曲线是由随钻声场特征函数的复极点的留数之和计算得到,并将图8b模拟结果与实验结果进行比较.图中T1,T2和T3分别表示一阶、二阶和三阶单极源钻铤波的激发强度曲线,In-St表示内斯通利波的激发强度曲线.对比结果表明:
(1) 两者在低频段的变化规律接近,都随着声源频率的提高而增大,只是理论计算曲线呈弧线形上升变化,与实验结果中的直线规律不同.
(2) 理论结果在90 kHz左右达到上升的峰值阶段,之后曲线迅速下降再上升,凹点突出,呈现了明显的禁带现象.
(3) 当声源频率超过禁带之后,理论曲线先呈大幅上扬的趋势,之后强度保持不变,这是理论计算与实验结果(阶梯状衰减)的最大不同.我们猜测理论和实验之间的差异性,可能是由于高频情况下压电片的激发能力减弱引起的.但具体原因目前还不清楚,也未见相关的理论和实验报道,因此,我们将在后续的工作中进一步探究钻铤波在高频下的响应规律,为测井数据解释提供参考.
3 地层纵波的随钻声波测量
我们在图1c所示砂岩模型中进行了单极源随钻声波测井实验,图9为压电片记录声波信号的时域波形和时间速度图.可以看到:除了速度4700 m·s-1的钻铤波信号,我们无法从测井全波和时间速度图中看到纵横波波群(纵波速度3900 m·s-1,横波速度2250 m·s-1).这说明钻铤波信号严重干扰了地层纵横波的测量.王军等(2016)指出,利用钻铤波和地层波激发频带的差异性,将声源频率选择在远离钻铤波但接近地层波最大响应的频率范围内,可降低钻铤波在全波中的相对幅值,从而有效测量地层声波速度.由前文图8知,图1a探头激发钻铤波的中心频率在100 kHz左右,而王军等(2015)电缆测井结果表明,当声源频率100 kHz时,本文所用砂岩模型井的纵横波响应最大.这说明钻铤波和地层波的最大响应频带重合,因此,我们不能通过改变声源激发频率的方法减弱钻铤波的影响.那么是否还有其他方法可以测量地层纵横波速度呢?通过分析随钻声波测井全波信号的成分可知(图3),换能器记录的声波信号由三部分组成:地层声波,内钻铤波和井壁反射的外钻铤波.所以笔者猜想,若能通过数据处理的方式,将内钻铤波和外钻铤波从测井全波中剔除出去,那么剩下的即为地层波信号,从而可准确测量纵横波速度.下面我们对上述方法的有效性进行了实验验证.
基于前文分析,我们在实验室内开展了三组测量工作:(1)在图1c砂岩模型井中进行了随钻声波测井实验,记录到了测井全波信号;(2)在图1b无限大流体模型中,利用压电片记录了内钻铤波信号;(3)在图1b无限大流体模型中,利用水听器记录了外钻铤波信号.三次实验保持所有测试仪器的设置不变:声源为负方波高压脉冲激励,电压200 V;前置放大器为40 dB,滤波器为1~300 kHz;采集卡分辨率为22位,采样率1 M.图10给出了上述三次实验的归一化波形.对比分析发现:三次实验均记录到了明显的钻铤波波群(速度4700 m·s-1),且图10a测井全波的钻铤波与内钻铤波(图10b)幅值接近,但均大于外钻铤波幅值(图10c).

图8 实验和理论获得钻铤波激发强度曲线的对比(a) 钻铤波激发强度的实验数据; (b) 钻铤波激发强度的理论数据.Fig.8 The comparison of excitation between the experimental and simulated collar wave(a) The experimental data of excitation intensity of collar wave; (b) The simulated data of excitation intensity of collar wave.

图9 随钻声波测井时域波形及时间速度图Fig.9 The time domain waveforms of LWD measurement and its semblance

图10 随钻声波测井信号与内外钻铤波时域波形图(a) 测井全波信号; (b) 内钻铤波; (c) 外钻铤波.Fig.10 The time domain waveforms of LWD signals and the collar waves(a) The LWD signals; (b) The inner collar wave; (c) The outer collar wave.
为了更直观地分析测井全波信号与内、外钻铤波的幅值关系,我们将三者放在一起进行对比(见图11).图中实线代表测井全波信号,点线分别代表内钻铤波(图11a)和外钻铤波信号(图11c),并进行了局部放大处理(见图11b和图11d).从图11可以看出测井全波中的钻铤波信号和内外钻铤波到时一致且相位相同,但三者的幅值却相差较大.图11b表明:测井全波中钻铤波的幅值与内钻铤波幅值接近,略大一些;但比图11d中外钻铤波的幅值要大得多.这说明测井全波中的钻铤波信号主要由内钻铤波提供,该结果与理论模拟结果(Yang et al.,2017)吻合.

图11 测井全波与内外钻铤波的对比(a) 测井全波信号和内钻铤波时域波形; (b) 放大后的测井全波信号和内钻铤波时域波形; (c) 测井全波信号和外钻铤波时域波形; (d) 放大后的测井全波信号和外钻铤波时域波形.Fig.11 The comparison between the LWD signals and the collar waves(a) The time domain waveforms of LWD signals and inner collar wave; (b) The magnified time domain waveforms of LWD signals and inner collar wave; (c) The time domain waveforms of LWD signals and outer collar wave; (d) The magnified time domain waveforms of LWD signals and outer collar wave.
接下来我们考虑如何将测井全波信号中钻铤波消除的问题,基于前文的分析,我们给出两种处理方式:(1)测井全波信号减去内钻铤波;(2)测井全波信号减内钻铤波减外钻铤波.图12为处理后的时域波形和时间速度图.以下是处理结果分析:
(1) 测井全波信号减去内钻铤波(图12a,b)

图12 两种测井全波数据处理(a) 测井全波信号减内钻铤波的时域波形图; (b) 时间-速度图; (c) 测井全波信号减钻铤波的时域波形图; (d) 时间-速度图.Fig.12 Two methods of data processing for the LWD signals(a) The difference between LWD signals and inner collar wave; (b) The time domain semblance; (c) The difference between LWD signals and collar wave; (d) The time domain semblance.
观察图12a可知,处理后的时域波形上记录到了两组波群,其速度分别为4700 m·s-1和3900 m·s-1.通过分析可知,前者为钻铤波的速度,后者为地层纵波速度.虽然纵波速度到时一致性匹配不是很完美,但与图9a对比可知,数据处理后的纵波波群清晰度明显提高,特别是第四和第五两道曲线,它们的到时和波群起跳与地层纵波速度吻合得非常好.另外,图12b时间速度图上也观察到了这两个波群,不过我们发现这两个波群在时间轴上都发生了平移.在本文实验系统中,钻铤波的预测到时应为t1=0.023 ms,地层纵波的到时应为t2=0.028 ms,经过处理后,钻铤波和地层纵波的到时皆向右平移了0.005 ms,此时,t2时刻对应钻铤波的亮点中心,t3=0.033 ms对应地层纵波信号.造成上述结果的原因是由于两组数据相减的过程导致波形发生了微小平移引起的,不影响处理后实验数据的正确性.
(2)测井全波信号减内钻铤波减外钻铤波(图12c,d)
观察图12c,d可以得到与图12a,b类似的结论,时域波形和时间速度图中都看到了钻铤波和地层纵波信号,表明两种处理方法均可有效抑制钻铤波对地层波的测量,而且两种处理方式得到的结果非常接近.比如,图12a和图12c时域波形的差别很难用肉眼进行区别,而图12b和图12d的时间速度图也相差不大,这说明外钻铤波的作用非常微弱.
需要指出的是:本文利用8103水听器记录的外钻铤波信号与现场测井情况的外钻铤波是有区别的.首先,接收器的灵敏度不同;其次,现场情况下井壁的反射会使外钻铤波的幅值发生变化,本文图12c结果便可证实这一点,因为图12c通过处理后(测井全波信号-内钻铤波-外钻铤波)的波形中还可以看到明显的钻铤波信号,说明井壁反射回来的外钻铤波信号比水听器记录信号要强,进而利用水听器的信号不能将钻铤波全波消除.另外,考虑现场测井情况下无法测量外钻铤波信号,因此,在实际应用过程中,可采用第一种方法进行数据处理.
上述实验结果验证了前文数据处理方法的有效性,虽然没有测量到地层横波信号,但我们从时域波形和时间速度图中准确获取了地层纵波速度.为了验证上述实验结果的可重复性,我们仅仅改变探头在井孔中的位置和采集卡的采样率(调至5 MS/s),重复进行上述三组实验,结果如图13所示.其中图13a为实验记录测井全波(实线)和内钻铤波(点线)的时域波形,分析发现:测井全波中的钻铤波信号与内钻铤波信号几乎完全重合,两者之间的幅值差异要比图12中小得多,进而在两者相减之后的波形图中(图13b)看不到钻铤波信号,只剩下清晰的地层纵波信号,图13c时间速度中纵波的响应也与时域波形吻合.
通过对比图12和图13实验结果可知,图13结果对钻铤波的抑制效果甚佳,处理后的测井全波中已经看不到钻铤波信号,从而准确提取到地层纵波速度.考虑到提高采样率可能会改善测井数据,但效果不会这么明显,所以推断改变探头在井孔中的位置是导致图13处理结果相对完美的主要原因.因为我们观察模型井的井孔发现,砂岩井孔中间位置有一段井壁不规则,这是取心过程多次操作造成的.但不规则的井壁增强了外钻铤波信号的反射,导致测井全波信号中钻铤波总量超过内钻铤波信号幅度较多(见图11b),进而在两者相减之后的时域波形中依然保留了钻铤波信号,该信号则影响了地层纵波速度的测量.当我们重复进行实验时,接收压电片幸运地避开了不规则井壁,使得测井全波中钻铤波信号与内钻铤波信号的幅度非常接近(图13a),这种情况下,两者相减结果中钻铤波信号几乎看不到了,从而准确测量地层纵波的速度.
通过图13结果还可看出,虽然图13c 时间速度图中依旧没有提取到地层横波速度,这是因为内钻铤波信号的拖尾较长,如图10b中持续到0.1 ms.但与测井全波相比,图13b时域波形图中横波信号的清晰度有较大改善,如图中第二、三、五道曲线中横波起跳与预测结果(代表2250 m·s-1的虚线)吻合很好.这说明本文方法对横波测量也是有效的.另外,本文图1测井探头没有进行刻槽处理,使得钻铤波信号的幅度很大,而实际测井设备会进行适当的内外刻槽处理,这样钻铤波信号的幅度会降低一些,若再利用本文数据处理方法,将有望利用现有技术准确测量到地层的纵横波速度.
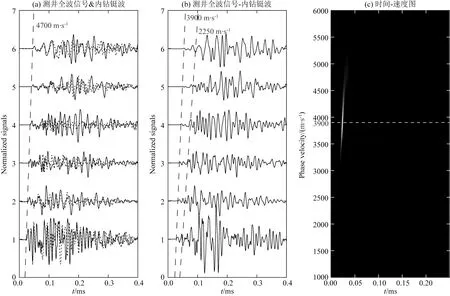
图13 测井全波数据处理(a) 测井全波信号及内钻铤波时域波形图; (b) 测井全波信号减内钻铤波的时域波形图; (c) 时间-速度图.Fig.13 The data processing for the LWD signals(a) The time domain waveforms of LWD signals and inner collar wave; (b) The difference between LWD signals and inner collar wave; (c) The time domain semblance.
4 结论
本文先在无限大流体模型中开展了随钻声波实验测量,记录了30~250 kHz频率范围内激发的单极源内、外钻铤波信号,研究了它们随声源频率变化的响应特性.在此基础上,我们在小尺寸砂岩模型井中进行了随钻声波测井实验,分析了测井全波中钻铤波信号与内外钻铤波的幅值关系,进而提出了随钻测量地层纵波速度的实验方法,主要结论如下:
(1) 随着声源激发频率的增加,内、外钻铤波的幅值-频率曲线均呈现出先增大后保持不变,再缓慢减小的规律.但两者在不同频率段的变化率不同:在低频段,内钻铤波的幅值增大更快;在峰值阶段,外钻铤波的频带更宽,且禁带现象更突出;在高频阶段,内外钻铤波均随着频率的提高而减弱,这与理论计算钻铤波的激发强度曲线截然相反.
(2) 对比分析了测井全波中钻铤波与内外钻铤波的幅值关系,实验结果表明:测井全波中的钻铤波信号主要是内钻铤波的贡献,外钻铤波提供的能量较小.但在井壁不光滑情况下,外钻铤波的贡献会增强,从而提高测井全波中钻铤波的幅值.
(3) 基于随钻声波测井信号的构成,本文提出了一种削弱钻铤波,进而从测井全波中提取纵波速度的方法.实验结果表明:通过测井全波与内钻铤波相减的方式可有效削弱,甚至消除测井全波中的钻铤波信号,从而准确测量地层纵波速度,同时也可改善横波波群的清晰度.本文实验结果验证了该方法的有效性和实验重复性,有望解决随钻声波测井提取纵波速度不准确的难题,对储层评价和测井数据解释非常有意义.
致谢感谢课题组胡恒山教授对本文工作的帮助和建议.
