偶应力理论框架下的弹性波数值模拟与分析
2021-05-07王之洋李幼铭白文磊
王之洋, 李幼铭 , 白文磊
1 北京化工大学信息科学与技术学院, 北京 100029 2 中国科学院地质与地球物理研究所, 中国科学院油气资源研究重点实验室, 北京 100029 3 非对称性弹性波动方程联合研究组, 北京 100029 4 高铁地震学联合研究组, 北京 100029
0 引言
地球介质是一种非均匀、非完全弹性、各向异性、多相态的介质(傅承义等,1985),在经典地震学理论框架下,先人发展了数不胜数的地震技术,为社会发展做出了巨大贡献;可是,当前技术仍有难以逾越的障碍,亟需破局.因此,寻求更接近真实地球介质的波动理论,构建更加符合物理实际的地球介质模型,是地球物理学发展的一个趋势.
2019年8月底,中国科学院地质与地球物理研究所、北京大学以及西安交通大学等单位组成的高铁地震学联合研究组,在河北省定兴县野外采集资料,检波器分别放置于高铁的高架桥沿线以及桥墩处.通过对中国科学院地质与地球物理研究所“高铁地震学研究协调办公室”提供的数据的分析,可以观察到大量的旋转运动分量.由于基于经典连续介质力学推导的弹性波动方程,从理论出发点上就去除了独立的旋转自由项,且在其理论框架内,介质被视为一个连续的质量体(Yang et al.,2002),事实上,不论是人造还是天然的介质都存在着复杂的内部结构(Zhu et al.,2019),没有介质是理想的连续统,广义连续介质力学更适合描述具有更加复杂内部结构的情况(Jirásek,2004).于是,我们尝试启用广义连续介质力学理论,推导偶应力理论框架下的弹性波动方程,将其表达形式以及数值模拟结果与传统弹性波动方程进行对比,研究发现推导的具非对称性的波动方程所具有的理论意义和应用价值.
传统地震学是基于经典的连续介质力学原理建立的,在该理论中,应用角动量守恒定律,我们可以得到应力张量是对称的结论.而对于广义连续介质力学,组成介质的每个点都被视为一个体积不为零的刚性微元体,微元体上可以承受均布的体力偶和面力偶以产生旋转的作用,在应用角动量守恒定律时,必然导致应力张量是非对称的.应力张量是否对称,或者说力学上是否具有对称性,是连续介质力学和广义连续介质力学的本质区别和重要差异.经典连续介质力学理论下的旋转运动,在小变形假设下,其不造成形变(Aki and Richards,2002),所以在小变形假设下,位移梯度全部用对称的应变张量表示是合理的.对于各向同性介质,旋转造成的位移扰动包含在横波分量里,可以通过求取位移旋度的二分之一获得旋转分量.而广义连续介质力学理论下的旋转运动则不完全相同,其是由于介质内部存在的微孔缝隙结构所导致的力学不对称性所产生的.
广义和经典连续介质力学理论是并行发展的两个分支,广义连续介质力学(Cosserat and Cosserat,1909;Mindlin and Tiersten,1962;Koiter,1964;Eringen and Suhubi,1964;Mindlin,1964,1965;Eringen,1966,1990,1999;Aifantis,1999;Yang et al.,2002;Lam et al.,2003;Askes and Aifantis,2011;Hadjesfandiari and Dargush,2011;Chen et al.,2011;Polizzotto,2013;Li et al.,2015;Gopalakrishnan,2016;De Domenico et al.,2019;Zhu et al.,2019)通过对经典连续介质力学基本假设、原理或者限制条件进一步放松,引入状态变量的高阶导数项,描述由假设偶应力存在而导致的介质内部微结构相互作用所产生的介质非均匀性,以丰富经典连续介质力学理论的内容.广义连续介质力学理论可追溯至19世纪末,其最基本的理论方法就是偶应力理论,其他理论方法分支就是在偶应力理论的基础上被建立起来的.Voigt(1887)指出关于物体的一部分对其邻近部分的作用可能引起体力偶和面力偶的猜想,并认为应力张量可能是非对称的.Cosserat和Cosserat(1909)验证了这个猜想,提出了Cosserat连续介质理论.在该理论中,每个组成介质的点都被看成是一个非零体积的刚性微元体,具有包括旋转和位移等6个自由度.Toupin(1962)对该理论进行了拓展,建立了完全弹性固体有限变形的本构关系.Mindlin和Tiersten(1962)将Toupin(1962)的理论进行了简化,其假定微元体与周围宏观介质的相对旋转为零,曲率张量表示为位移的二阶梯度,建立了约束转动的偶应力理论,至此,偶应力理论的框架被基本建立起来.Yang等(2002)引入高阶力矩平衡理论,提出仅具有一个材料尺度参数的改进Cosserat连续介质理论,这一理论也被称为修正的偶应力理论(Park and Gao,2006;Ma et al.,2008;Kong et al.,2008).Hadjesfandiari和Dargush(2011)提出了与Yang等(2002)完全相反的偶应力理论,他们认为介质的应变能密度函数与经典应变张量以及曲率张量的反对称部分有关,而与曲率张量的对称部分无关.通过对实验数据和实际应用的分析,Yang等(2002)的理论更加符合物理实际(Reddy and Kim,2012;Jung et al.,2014;Shaat et al.,2014;王之洋等,2020).Chen等(2011)提出了一种新的修正的偶应力理论,并将其推广到各向异性介质.
本文研究推导偶应力理论框架下的具非对称性的弹性波动方程,并应用该方程进行数值模拟试验,将合成记录与传统弹性波动方程的合成结果以及实际数据进行对比分析,研究包含介质特征尺度参数的具非对称性的弹性波动方程对地震波传播的影响与规律.本文首先从经典平衡方程、几何方程和本构方程出发,在经典平衡方程中加入体力偶和面力偶的成分,在几何方程中新增加对称曲率张量和位移高阶导数的关系,在本构方程加入对称曲率张量和对称偶应力张量的关系,构建新的平衡方程、几何方程和本构方程,并推导偶应力理论框架下包含介质特征尺度参数的非对称弹性波动方程的数学表达式,同时,描述引入的旋转自由项以及介质特征尺度参数的物理意义.其次,在均匀介质模型和Marmousi模型上进行数值模拟测试,并将数值模拟结果与传统弹性波动方程的数值模拟结果进行对比,分析非对称弹性波动方程所增加的旋转自由项对地震波传播的影响.最后,在高铁桥墩模型上进行数值模拟试验,并与实际数据以及传统弹性波动方程的合成记录进行对比,进一步研究分析介质特征尺度参数和旋转自由项对地震波传播的影响.
1 偶应力理论框架下的弹性波动方程
相比于传统弹性波动方程的推导,平衡、几何、本构三组方程的基本形式没有改变,只是对其进行了拓展和补充.基于此逻辑,推导得到的偶应力理论框架下的弹性波动方程只会在传统方程的基础上增加了旋转自由项,其通过位移的高阶导数描述由力学不对称特征所导致的旋转运动.如果去掉此旋转自由项,偶应力理论框架下的弹性波动方程就和传统弹性波动方程有一致的数学表达.
1.1 平衡方程
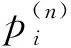
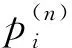
(1)
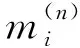
(2)
应力张量σij和偶应力张量μij均满足线动量平衡方程(公式(3))和角动量平衡方程(公式(4)):
(3)
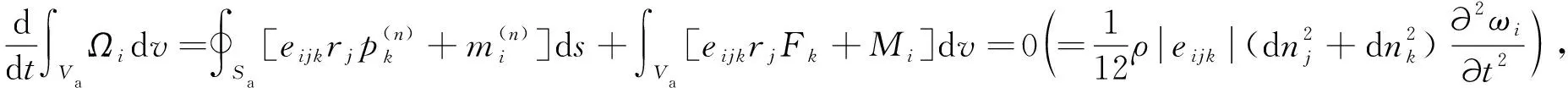
(4)
其中,Vi,Ωi分别为线动量和角动量.Fi,Mi分别是体力和体力偶.eijk为置换符号.rj是位矢.ui是位移矢量,ωi是旋转矢量.
对公式(3)和(4)分别应用散度定理,由表面积分变换为体积分,则公式(3)和(4)可改写为:
(5)
(6)
从公式(6)中可略去高阶微量,由公式(5)和(6)可以分别得到微分形式的平衡方程:
(7)
μji,j+eistσst+Mi=0.
(8)
公式(7)和(8)可分别展开为:
(9)
(10)
在经典连续介质力学中,没有考虑偶应力与体力偶的作用,也即μij=0,Mi=0,因此,可由公式(8),得到:
eistσst=0.
(11)
公式(11)表明,经典连续介质力学理论框架下,应力张量是对称的.这就意味着应力张量有6个独立量,这里有3个平衡方程,另外的3个方程为本构方程,6个方程可以定解.
而在偶应力理论中,当考虑偶应力或体力偶时,切应力互等定理不成立了,这导致应力张量的不对称性,这时候,应力张量σij可以分解为对称应力张量τij与反对称应力张量rij之和:
(12)
如果将公式(12)代入公式(7)和(8),将应力张量σij用对称应力张量τij与反对称应力张量rij表示,则公式(7)和(8)可以改写为:
(13)
μji,j+eistrst+Mi=0,
(14)
其中,s,t=1,2,3.
同时基于公式(8),建立反对称应力张量rij与偶应力张量μij的关系式:
(15)
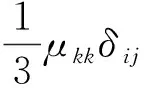
(16)
将公式(15)等号两边求散度,并将公式(16)代入,可得:
(17)
将公式(12)和(17)一齐代入公式(13),可消除反对称应力张量rij,得到只包含对称应力张量τij以及偶应力张量的偏斜部分mij的平衡方程:
(18)
公式(18)即为偶应力理论框架下的平衡方程,其构建了偶应力张量、应力张量、体力偶和体力的关系,如果去除了偶应力张量和体力偶,该平衡方程就为经典理论的平衡方程.
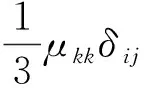
进一步探讨偶应力张量μij的对称性.Yang等(2002)基于连续体内偶力矩为零的假设,引入了高阶力矩平衡关系,对偶应力张量μij施加了约束,见公式(19):
(19)
对公式(19)应用散度定理,可得:
(20)
因为μji,j+eistσst+Mi=0,可得eistμst=0,即偶应力张量μij是对称的.
1.2 边界条件
考虑不存在体力和体力偶的单位体积元能量守恒(Hadjesfandiari and Dargush,2011):
(21)
其中,n是方向矢量,δu为虚位移矢量,δω为虚旋转矢量,δw为能量改变量.
因为有:
n·μ·δω=n·μ·nn·δω+n·μ·(I-nn)·δω
(22)
其中,nn,(I-nn)分别代表法向和切向方向.
对公式(22)等号右边第一项应用Hamiltonian算子,可得:
(23)
并考虑表面Sa是光滑的,即有:
(24)
则公式(21)可写为:
(25)
公式(25)表明,因为表面Sa上偶应力张量的法向分量μn n与应力张量σij的组合作为δu的系数,因此在偶应力介质中仅仅包含5个边界条件,即应力矢量p(n)的3个分量以及力偶矢量m(n)的2个切向分量.
由公式(25),可得到偶应力理论框架下的边界条件:
(26)
m(n)=n·μ·(I-nn).
(27)
真实的边界上一般没有力矩作用,这意味着真实边界上自然边界条件处处为零,即m(n)=0.但偶应力张量μij在物体内部却会产生,在任意体积(包括了微元体积)的表面上却存在着非零的m(n).
1.3 几何方程
这里仅仅考虑微小变形|ui,j|≪1的运动学(几何方程).在笛卡尔坐标系中,参考构型中的两点A(位置为xi)和B(位置为xi+dxi)之间的相对位移为(Aki and Richards,2002):
dui=ui,jdxj,
(28)
位移梯度张量ui,j可分解为对称的无穷小应变张量εij和反对称的无穷小旋转张量ωij之和:
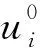
(29)
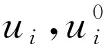
(30)
(31)
(32)
因此,旋转矢量ωi可以通过求取位移场旋度的二分之一得到.
在微小变形|ui,j|≪1假设下,经典连续介质力学理论下的旋转运动,是刚性旋转,其不造成形变(Aki and Richards,2002),位移梯度可以全部用对称的应变张量表示.偶应力理论下,引入了一种假设偶应力存在而出现的新的旋转运动,使微元线段dxi产生了扭转和弯曲形变,其由相邻两点A,B之间的相对转动dωi描述,并引入对称的曲率张量ij描述这种形变(Yang et al.,2002):
dωi=ωi,jdxj,
(33)
这样,在微小变形中,连续体A点临近B点的形变总结起来有4种:随着A点的平动,相对A点的伸缩,相对A点的转动以及微元线段AB的扭转弯曲.
通过构建曲率张量以及应变张量与位移的关系,我们可以推导得到几何方程,相比于经典理论的几何关系,偶应力理论框架下增加了曲率张量与位移之间的关系,几何方程见公式(34):
(34)
1.4 本构方程
由虚功原理,在公式(7)两端乘以虚位移δui,在公式(8)两端乘以虚旋转δωi,并在整个体积Va上积分,可得(Koiter,1964):
(35)
(36)
对公式(35)和(36)应用链式求导法则以及散度定理,并相加,可得:
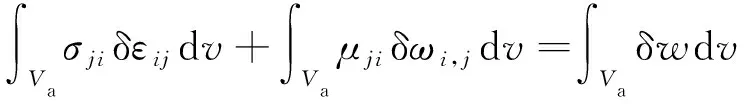
(37)
将公式(1)和(2)代入公式(37),并应用散度定理,将公式(37)等号右边第一项的面积分变为体积分,可得:
(38)
将平衡方程(公式(18))、几何方程(公式(34))以及公式(12),代入公式(38)并化简,可得功共轭关系:
(39)
对于各向同性介质,应用广义胡克定律以及功共轭条件(公式(39)),可得偶应力理论框架下的本构方程:
(40)
其中,λ,μ为Lamé常数,η为反映介质微旋转运动特性的参数,η=μl2,l为介质特征尺度参数,其是为了平衡无量纲的应变和有量纲的曲率张量(其量纲为长度的倒数)两项间的量纲,也为了描述偶应力张量和曲率张量之间的本构关系.
1.5 偶应力理论框架下的弹性波动方程
对于各向同性介质,将几何方程(公式(34))和本构方程(公式(40))以及平衡方程(公式(18))联立,并忽略体力以及体力偶,可推导得到偶应力理论框架下的弹性波动方程:
(41)
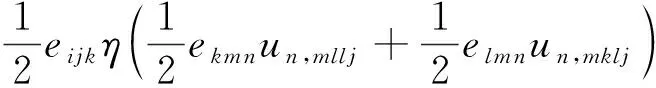
旋转自由项中的η是介质内部微结构相互作用导致的旋转效应的表征,如果η=0,则旋转效应消失,偶应力理论框架下的弹性波动方程就和传统弹性波动方程有一致的数学表达.Teisseyre和Boratńyski(2003)通过理论推导证明,在颗粒介质或者有裂隙的连续体内,由于微缺陷/微结构的存在,应力或者应力场会出现不对称性力学特征,由此产生一种新的旋转运动.Bažant(2002)认为金属材料的微缺陷/微结构一般由晶体的位错引起,晶体位错在纳米量级;而岩土介质的微缺陷/微结构一般是由微夹杂/微裂缝/微孔隙/孔洞等引起,尺度可以在微毫米或更高量级.黄文雄和徐可(2014)通过实验证明,介质特征尺度l与组成介质的材料颗粒平均直径以及几何形状有关,同时,也与变形局部化现象有关.另外,与应力集中效应也有关(鲍亦兴和毛昭宙,1993).如果忽略一切附加因素,介质特征尺度参数可直接视为介质微孔缝隙特征尺度参数.相反,如果考虑组成介质的材料颗粒的几何特征、变形局部化现象以及应力集中效应,介质特征尺度参数可视为介质微孔缝隙特征尺度参数与系数ζ相乘的结果,系数ζ可通过实验获得,王之洋等(2020)通过对高铁实际数据和理论合成数据的对比分析,也提取了该系数.当然,为了进一步研究介质特征尺度参数和旋转自由项的物理意义,必须结合岩石物理测量,开展对比验证研究和技术生成.
2 数值模拟与分析
2.1 均匀各向同性介质模型
首先,我们构建均匀各向同性介质模型,模型大小为nx=nz=400,网格间距为dx=dz=8 m,纵波速度为2.0 km·s-1,横波速度为1.1547 km·s-1,密度为2000 kg·m-3,采用主频为25 Hz的Ricker子波,并在模型中间激发,时间步长Δt=0.001 s,介质微孔缝隙特征尺度参数为200 μm.为了排除数值频散和边界反射对数值模拟结果的影响,我们采用高阶优化有限差分算子以及优化的PML(Perfectly Matched Layer,完全匹配层)边界条件进行数值模拟,以更好地对传统弹性波动方程以及偶应力理论框架下的弹性波动方程的合成记录进行对比分析.
图1和图2分别是应用传统弹性波动方程和偶应力理论框架下的弹性波动方程进行数值模拟所得到的x分量和z分量的合成波场快照.从图1和图2中可以看出,不论是x分量,还是z分量,偶应力理论框架下的弹性波动方程增加的旋转自由项所带来的位移扰动都对地震波传播带来了明显的影响,出现了新的波场分量.比较图1a和图1b的x分量波场快照,偶应力理论框架下的旋转运动,对纵波没有影响,但却使得横波在传播过程中出现了物理频散,如果将图1a和图1b相减,可以更加清晰地观察到横波波场的变化.图2中z分量波场快照的比较,同样可以得到此结论.
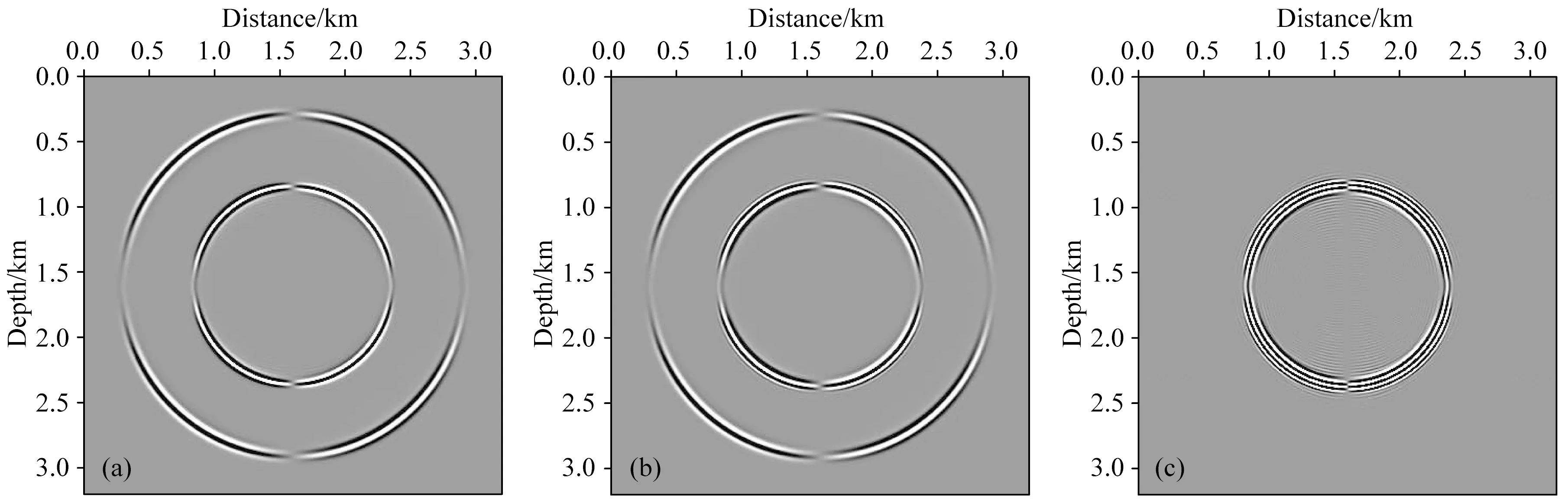
图1 应用不同弹性波动方程得到的合成波场快照(x分量)(a) 传统弹性波动方程; (b) 偶应力理论框架下的弹性波动方程; (c) 图(a)和图(b)的差值.Fig.1 Synthetic wavefield snapshots (x component) using different elastic wave equations(a) The conventional elastic wave equations; (b) Elastic wave equations in the frame of the couple stress theory; (c) The difference between figure (a) and figure (b).
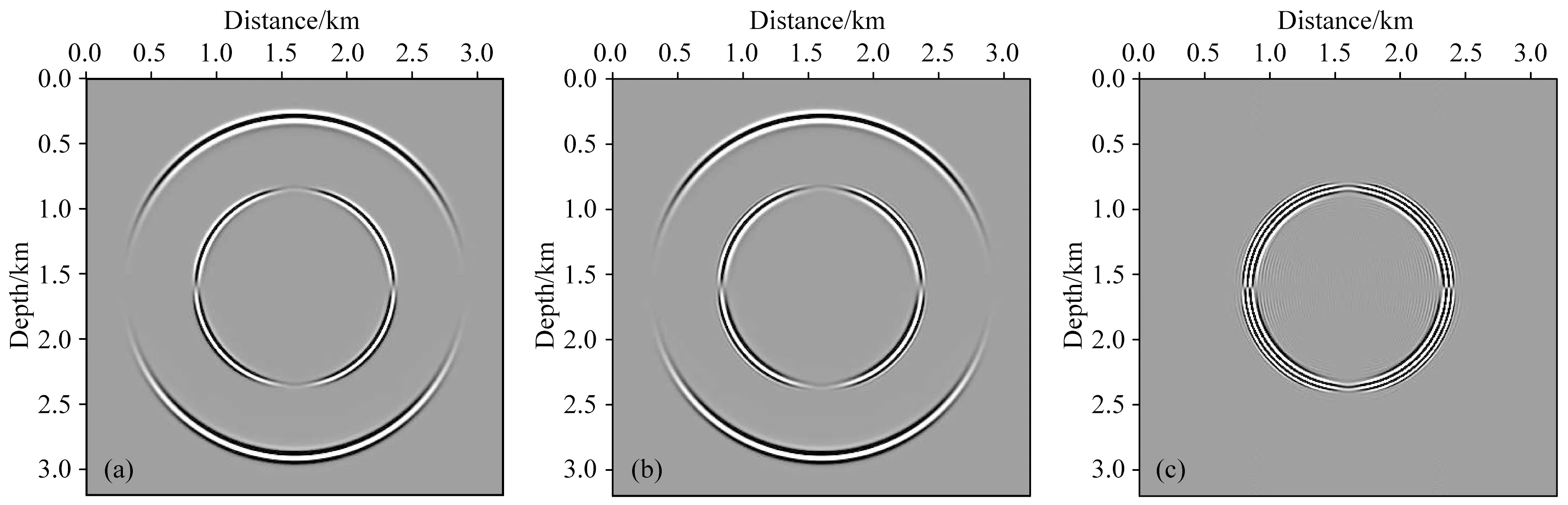
图2 应用不同弹性波动方程得到的合成波场快照(z分量)(a) 传统弹性波动方程; (b) 偶应力理论框架下的弹性波动方程; (c) 图(a)和图(b)的差值.Fig.2 Synthetic wavefield snapshots (z component) using different elastic wave equations(a) The conventional elastic wave equations; (b) Elastic wave equations in the frame of the couple stress theory; (c) The difference between figure (a) and figure (b).
偶应力理论框架下的弹性波动方程包含独立的旋转自由项,可描述由考虑介质内部微孔缝隙结构相互作用所带来的旋转运动以及其位移扰动的传播,这种位移扰动可以在合成记录中被清晰地观察到,同时,该旋转运动对纵波没有影响,而使横波的波场出现了新的成分,导致其以频散的方式传播.
2.2 Marmousi模型
为了进一步对比应用传统弹性波动方程和偶应力理论框架下的弹性波动方程得到的合成地震记录的差异,我们在Marmousi模型上进行测试.速度模型大小为737×750,横向采样间隔为12.5 m,纵向采样间隔为4 m,密度ρ=1500 kg·m-3,横波速度和纵波速度的比值为vp/vs=1.7.采用主频为25 Hz的Ricker子波,震源位置设置在模型顶层中间处,时间步长Δt=0.0005 s,记录时长为t=10 s,同样,设置介质微孔缝隙特征尺度参数也为200 μm.
图3和图4分别是应用传统弹性波动方程和偶应力理论框架下的弹性波动方程对Marmousi模型进行数值模拟所得到的x分量和z分量的合成地震记录.对于较复杂的Marmousi模型,介质内部孔缝隙所带来的位移扰动的影响依然存在,从图3和图4中可以清晰地观察到,相比于应用传统弹性波动方程得到的合成地震记录,偶应力理论框架下的弹性波动方程下合成地震记录,在图中红色箭头标示区域,存在新的波场扰动,即使我们设置的介质微孔缝隙特征尺度参数在微米量级,相比于子波波长,量级上的差距巨大,但其所带来的对地震波传播的影响仍然能够在地震记录上被观察到.由于采用高阶优化的差分算子进行数值模拟,数值频散已经得到了有效的压制,因此,图3c和图4c中观察到的地震波场差异,有理由相信,是地震波传播中出现的物理频散.
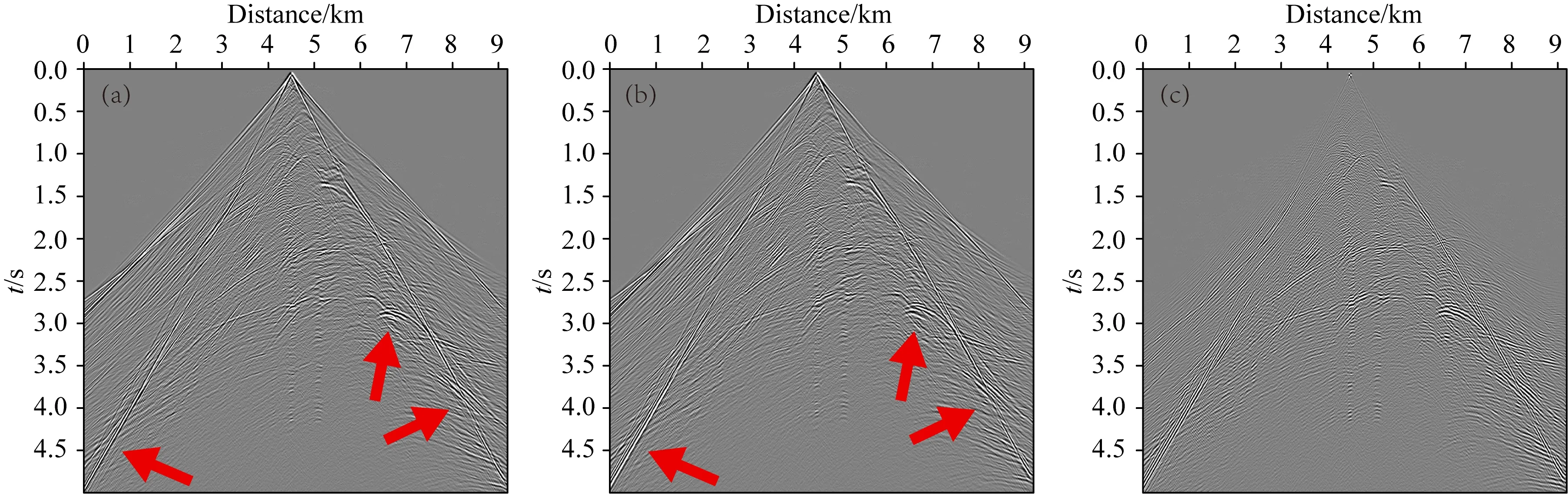
图3 在Marmousi模型上应用不同弹性波动方程得到的合成地震记录(x分量)(a) 传统弹性波动方程; (b) 偶应力理论框架下的弹性波动方程; (c) 图(a)和图(b)的差值.Fig.3 Synthetic shot records (x component) for Marmousi model using different elastic wave equations(a) The conventional elastic wave equations; (b) Elastic wave equations in the frame of the couple stress theory; (c) The difference between figure (a) and figure (b).
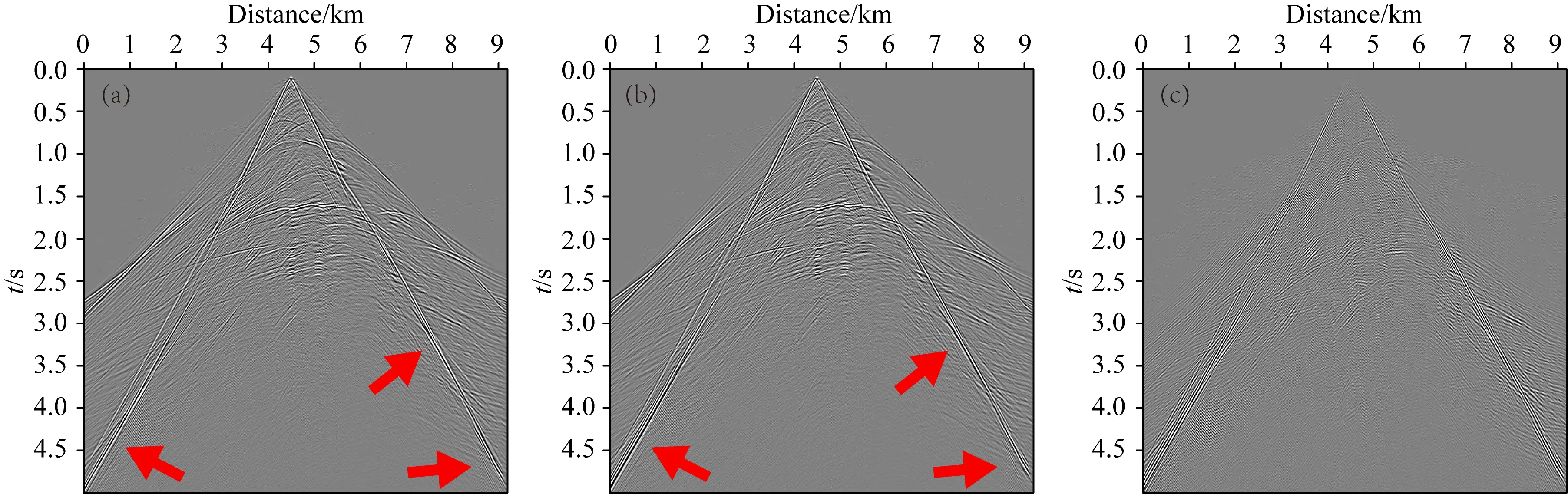
图4 在Marmousi模型上应用不同弹性波动方程得到的合成地震记录(z分量)(a) 传统弹性波动方程; (b) 偶应力理论框架下的弹性波动方程; (c) 图(a)和图(b)的差值.Fig.4 Synthetic shot records (z component) for Marmousi model using different elastic wave equations(a) The conventional elastic wave equations; (b) Elastic wave equations in the frame of the couple stress theory; (c) The difference between figure (a) and figure (b).
2.3 高铁桥墩模型
最后,我们应用偶应力理论框架下的弹性波动方程,在高铁桥墩模型上进行数值模拟试验,并将合成地震记录与应用传统弹性波动方程得到的合成地震记录进行对比.
我们构建了一个基于高铁列车震源的简化桥墩模型.速度模型大小为400×100,网格间距为1 m×1 m,分为两层,第一层是厚度为10 m的低速土壤层,密度为400 kg·m-3,纵波速度为0.5 km·s-1;第二层是厚度为90 m的高速围岩层,密度为1400 kg·m-3,纵波速度为1.6 km·s-1,横波速度和纵波速度的比值为vp/vs=1.7.桥墩数量为3个,桥墩间距为28 m,每个桥墩插入地下50 m深度直达围岩,每个桥墩的地下部分被看作是间隔为10 m的5个点源,地震波在桥墩中的传播速度为vp=4000 m·s-1.高铁列车车厢为16节,每节车厢的长度为28 m,列车速度为300 km·h-1,视为多个移动Ricker震源的叠加,Ricker子波主频设置为20 Hz,时间步长Δt=0.0005 s,记录时长为t=10 s,设置表层土壤和深层围岩的微孔缝隙特征尺度参数均为700 μm.基于高铁列车震源的简化桥墩模型如图5所示.
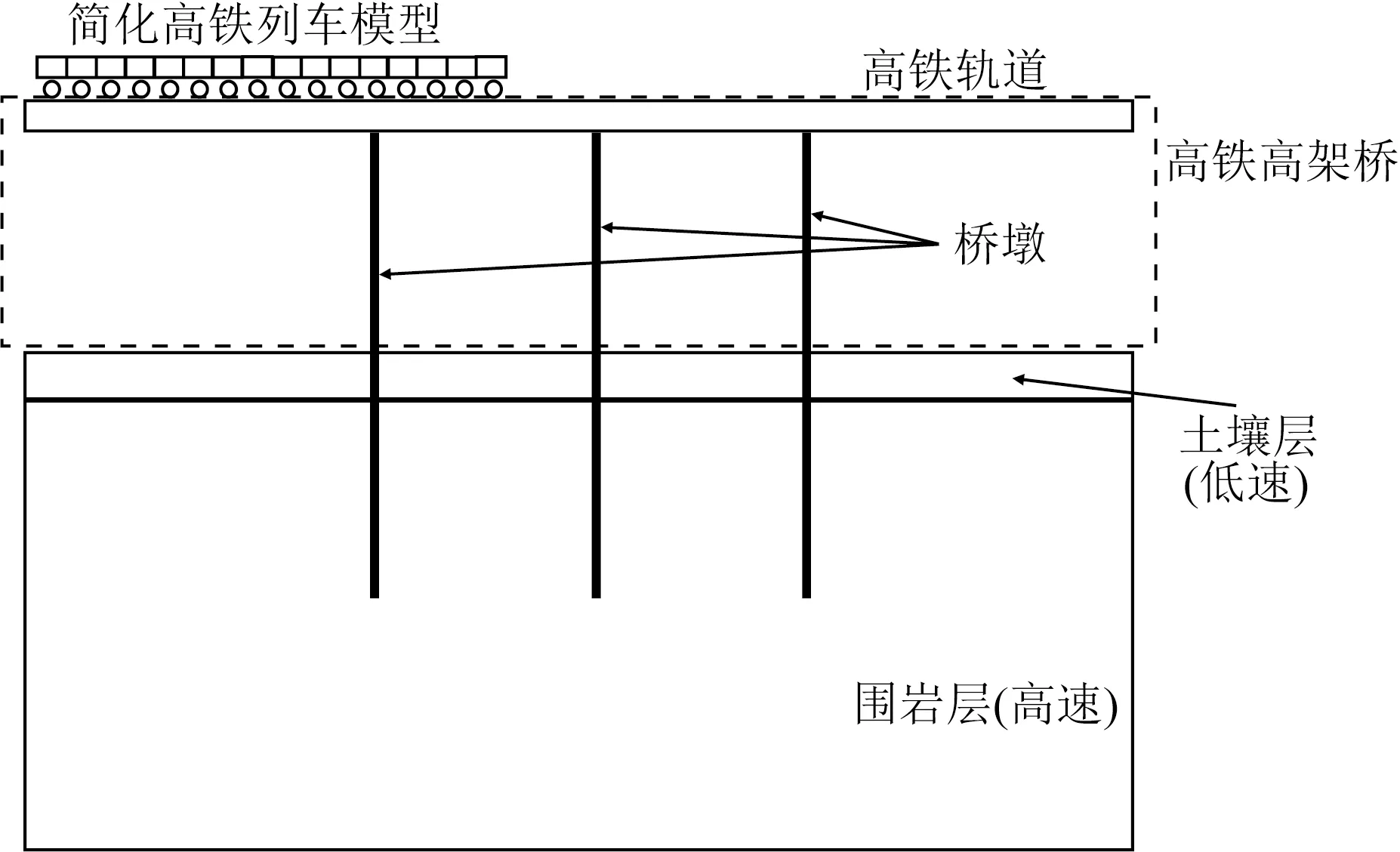
图5 基于高铁列车震源的简化桥墩模型Fig.5 A simplified bridge pier model of the source based on high-speed trains
图6是不同弹性波动方程得到的合成地震记录(z分量).从图6可以观察到,应用传统弹性波动方程和偶应力理论框架下的弹性波动方程所得到的合成地震记录在时域上的波形相似,我们的合成地震记录可视为不同空间位置的以一定时间间隔激发的固定震源记录的线性叠加,基于线性叠加的特性,可以通过设置模型参数,使模型的桥墩和桥梁长度和实际情况更加接近,从而使时域合成地震记录与实际记录具有更好的一致性.通过对频谱的分析,我们发现,当设置高速列车车速为300 km·h-1时,合成地震记录的能量集中在大约10 Hz以及25 Hz左右,其中,频率10 Hz附近的能量最大,这与实际高铁地震记录的频谱能量分布基本相符.
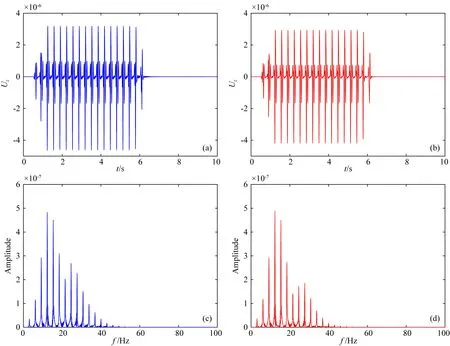
图6 不同弹性波动方程得到的合成地震记录(z分量)(a) 传统弹性波动方程; (b) 偶应力理论框架下的弹性波动方程; 图(c),(d)分别是图(a),(b)的幅度频谱.Fig.6 Synthetic shot records using different elastic wave equations (z component)(a) The conventional elastic wave equations; (b) Elastic wave equations in the frame of the couple stress theory; Figures (c) and (d) are the amplitude spectrum of figures (a) and (b), respectively.
进一步分析,将传统弹性波动方程和偶应力理论框架下的弹性波动方程所得到的合成地震记录在时频域进行对比,见图7.通过对图7的观察,我们发现,由于引入了包含介质特征尺度参数的旋转自由项,应用偶应力理论框架下的弹性波动方程所得到的合成地震记录在时间域波形上出现了衰减,其幅度频谱相较于传统弹性波动方程的合成记录,大于20 Hz的频谱能量都出现了小幅衰减,其中,20 Hz到30 Hz频段的能量衰减相对最大,且整体能量向低频10 Hz处移动,更趋近于实际高铁地震记录的频谱.我们认为,由于考虑了介质内部的微孔缝隙结构相互作用,应用偶应力理论框架下的弹性波动方程进行数值模拟,可以进一步增强地层的滤波效应.
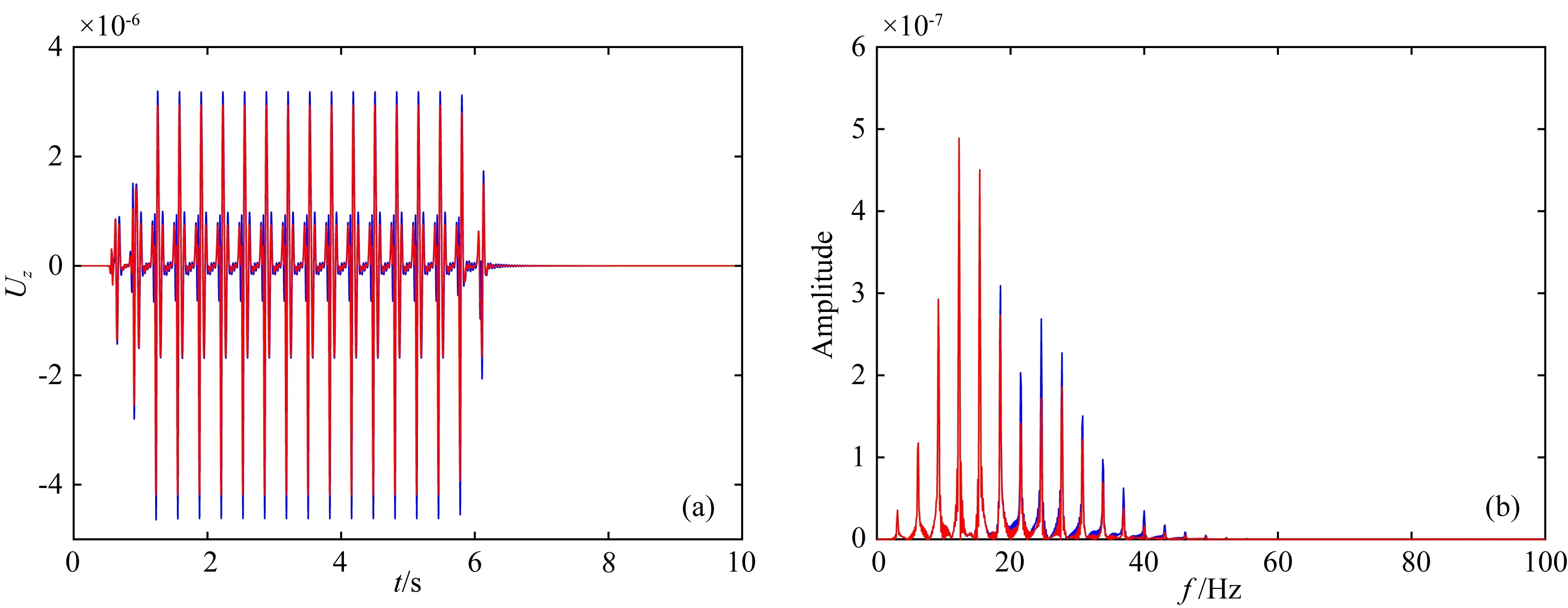
图7 合成地震记录对比(z分量)(a) 时域波形对比; (b) 幅度频谱对比.蓝线为使用传统弹性波动方程得到的合成地震记录,红线为使用偶应力理论框架下的弹性波动方程得到的合成地震记录.Fig.7 Comparison of synthetic shot records (z component)(a) The waveform comparison in time domain; (b) The comparison of the amplitude spectrum. The blue line is the synthetic shot record using the conventional elastic wave equations, and the red line is the synthetic shot record using elastic wave equations in the frame of the couple stress theory.
3 结论
本文尝试启用广义连续介质力学理论,推导偶应力理论框架下的弹性波动方程;将其数学表达形式以及数值模拟结果与传统弹性波动方程进行对比.研究探索推导的具非对称性的波动方程所具有的理论意义和应用价值.
本文推导的偶应力理论框架下的弹性波动方程,相比传统弹性波动方程,既增加了独立的旋转自由项,又引入了介质特征尺度参数,描述由介质内部微孔缝隙结构相互作用产生的不均匀性所导致的旋转运动以及其位移扰动的传播.旋转自由项中的参数η是反映介质微旋转运动特性的参数.如果η=0,则旋转效应消失,偶应力理论框架下的弹性波动方程就和传统弹性波动方程有一致的数学表达.
通过对均匀模型和Marmousi模型上的数值模拟结果对比分析,可以发现,考虑介质内部微孔缝隙相互作用所带来的位移扰动对地震波传播的影响是存在的,介质微孔缝隙结构的特征尺度,相比于子波波长,量级上的差距是巨大的,但其所带来的对地震波传播的影响仍然能够在地震记录上被观察到.另外,偶应力理论框架下的旋转运动,对纵波没有影响,但却使得横波在传播过程中出现了物理频散.为了进一步研究分析介质微孔缝隙相互作用对地震波传播的影响,我们在高铁桥墩模型上应用不同的弹性波动方程进行数值模拟试验,并将合成地震记录与高铁实际记录进行对比,结果表明,即使介质微孔缝隙结构的特征尺度为微米量级,合成的地震波场仍然出现了衰减,且其频谱能量往低频端移动.这表明介质内部的微孔缝隙结构相互作用可以增强地层的滤波效应,同时,也说明了地震记录对介质微孔缝隙结构的敏感性,可以启发后续的介质内部微孔缝隙特征尺度参数反演的研究.
致谢感谢中国科学院地质与地球物理研究所、北京大学和西安交通大学提供的数据支持,感谢中国科学院地质与地球物理研究所提供的计算资源.
