最小二乘Kirchhoff射线束叠前时间偏移
2021-05-07刘俊成陈祥忠郭井学王瑞星惠梦琳黄申硕
刘俊成, 陈祥忠 , 郭井学, 王瑞星, 惠梦琳, 黄申硕
1 吉林大学地球探测科学与技术学院, 长春 130026 2 北京桔灯地球物理勘探股份有限公司, 北京 102200 3 中国极地研究中心, 上海 200129
0 引言
地震偏移成像是地震数据处理过程中的重要环节(Schneider, 1978; Stolt et al., 1987; Baysal et al., 1983; Claerbout, 1992; Gray et al., 2000; 王华忠等,2009;孙小东等,2020),其不但可以用于恢复地下的构造信息,还可以估算地下的岩性和物性参数用于后续的地震反演和储层预测.按照偏移速度的不同定义方式,地震偏移方法可以分为两大类:时间偏移和深度偏移.深度偏移可以适应地下介质速度的剧烈横向变化,是复杂介质成像的首选技术手段,但其实际应用效果严重依赖于速度建模的精度.时间偏移虽然无法对复杂构造进行准确的成像,但当速度横向变化相对平缓时,其依然可以满足大部分工区的成像处理需要.此外,相对于深度偏移,时间偏移的计算效率更高,所需偏移速度也更容易估算.因此,即便在计算机硬件高度发达的今天,时间偏移依然是业界广泛使用的地震成像方法.
众所周知,常规的偏移方法只是地震波场正演算子的共轭转置(Tarantola, 1984; Claerbout, 1985),对于有限观测系统所采集的带限地震数据,其只能生成模糊的地下构造成像结果.此外,复杂的地下介质构造和非规则的地震数据空间采样,还会导致偏移假象和非规则的成像照明,严重影响成像振幅信息的可靠性.基于线性化地震反演理论的最小二乘偏移(Least-Squares Migration, LSM)是解决上述问题的有效手段(Nemeth et al., 1999; Duquet et al., 2000; Dai and Schuster, 2013; Hu et al., 2016; Yue et al., 2019;周东红等,2020;刘国章等,2020;刘玉敏等,2021).其将地震偏移视为线性反问题,并利用最优化方法求取能够准确模拟采集地震数据的成像剖面作为地下真实反射率,在理论上能够消除非规则采集、带限子波等因素对成像结果的不利影响.但是,LSM每次迭代均需一次正演和偏移运算,完整的LSM反演过程往往需要几十倍于常规偏移的计算量,庞大的计算成本严重影响了该技术的应用前景(张宇,2018).
本文将地震数据的局部平面波合成/分解策略(Hill, 2001; Gray, 2005; Liu and Palacharla, 2011; 岳玉波等,2012;李江等,2016;袁茂林等,2016;陈祥忠等,2020)应用于Kirchhoff正演/偏移(KFM/KTM)中,推导了高效的Kirchhoff 射线束正演/偏移(KBFM/KBTM)算子,并以此为基础发展了一种快速的最小二乘Kirchhoff射线束叠前时间偏移(LSKBTM)方法.同需要逐道映射运算的最小二乘Kirchhoff叠前时间偏移(LSKTM)相比,LSKBTM中数据空间和成像空间之间的数据映射运算仅需在稀疏的射线束中心位置进行,因此其计算成本大幅度降低.文中利用二维模型和二维、三维实际数据对LSKBTM进行了测试,其结果证明,LSKBTM可以有效的提高偏移结果的分辨率和照明度,其反演成像精度和残差收敛速度同LSKTM相当,但计算效率得到了大幅度提升.
1 方法原理
1.1 LSM基本原理
LSM可被视为一个最优化反演问题,其通过迭代的方式求取能够准确模拟接收记录的成像剖面,并将其作为地下真实的反射率(Tarantola, 1984).LSM的目标函数可以定义为
J=‖LR-d‖2+μ‖R‖2,
(1)
式中右侧第一项为数据匹配项,用于对地下反射率R的反演更新,第二项为保证反演稳定引入的正则化项,μ为控制正则化程度的参数,d为接收地震记录,L为线性化波场正演算子.式(1)所示的LSM目标函数一般通过梯度类算法(如共轭梯度法)进行迭代求解,其核心在于正演算子L以及共轭算子LT的构建.接下来,本文在时间域KFM/KTM算子引擎的基础上,通过引入地震数据的局部平面波分解/合成策略,推导高效的KBFM/KBTM算子,并以此为基础实现LSKBTM.
1.2 KFM/KTM算子
基于体积分表征的Kirchhoff正演公式(Bleistein, 2001)可以表示为
D(rd,rs,ω)=
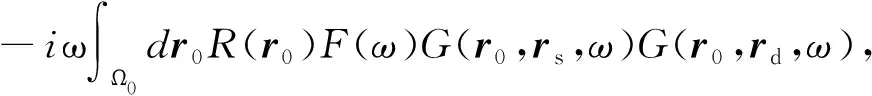
其中,Ω0代表地下散射点的集合,D(rd,rs,ω)为所模拟的单炮地震记录,F(ω)是震源频谱,R(r0)为地下散射点r0=(x0,y0,t0)处的反射率,G(r0,r′,ω)为震源在r′=(x′,y′,0)、观测点在r0处的格林函数,其在高频射线理论下可以表示为
G(r0,r′,ω)=A(r′)exp[iωT(r′)],
(3)
其中,T(r′)为地震波由震源到观测点的单程走时,在时间偏移中一般应用单平方根公式进行计算:
(4)
A(r′)为传播振幅,其在时间域的简化表达形式可以参照Zhang等(2000)中的相关内容.
×exp{iω[T(rs)+T(rd)]},
(5)
同时,求取式(5)的共轭转置可以得到相应的KTM算子:
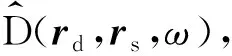
(6)
由式(5)和式(6)不难看出,KFM/KTM需要逐道进行地震数据和成像剖面间的数据映射运算,其计算量与地震数据的总道数呈正比关系.由于采集地震数据往往存在密集的空间采样,因此根据局部平面波合成/分解策略可将其转化为稀疏射线束位置的局部平面波,以此为基础实现KBFM/KBTM可以显著降低地震数据和成像结果间的映射运算次数,从而降低LSM的计算量.
1.3 KBFM算子
首先,应用基于高斯窗的单位分解算法(Hill, 2001; Hu et al., 2016; Yue et al., 2019)对式(5)两侧进行加窗处理:
(7)
其中,L代表高斯窗中心位置,也称为射线束中心,其采样间隔ΔL=(ΔLx,ΔLy),ωr为参考频率.此时,式(5)可以转化为
(8)

接下来,用射线束中心振幅A(L)来近似式(8)中的振幅项A(rd),并走时T(L)的一阶泰勒展开来近似(8)中的走时项的T(rd):
(9)
此时,式(8)可以转化为
×exp{iω[T(rs)+T(L)]}
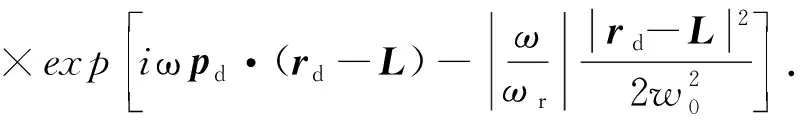
(10)
如果将对应接收点射线参数为pd的散射点的集合定义为Ω0(pd),那么式(10)可以表示为
(11)
其中:
×exp{iω[T(rs)+T(L)]}.
(12)
最后,分别对式(11)和式(12)应用傅氏反变换,得到最终的时间域KBFM算子:
⊗s(L,pd,t-pd·(rd-L)),
(13)
其中,d(rd,rs,t)为模拟炮集地震记录,符号⊗代表褶积运算,γ(rd,t)为高斯窗的时间域响应函数,s(L,pd,t)为在射线束中心处合成的局部平面波:
×A(L)δ(t-T(rs)-T(L)),
(14)
其中,δ为delta函数,f(t)为式(15)所定义的时间域子波信号:
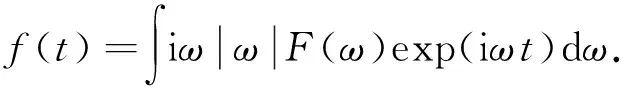
(15)
利用KBFM进行单炮模拟的计算过程可以大致概括为:
(1)确定射线束中心宽度ΔL,初始束宽度w0,射线参数采样间隔Δpd等计算参数.
(2)对于每一个射线束中心L,进行地下散射点的循环,计算式(14)中的走时、振幅等参数,并以此为基础将地下反射率映射转换到τ-p域.
(3)重复步骤(2)直到所有射线束中心处理完成,然后计算τ-p域地震道同子波f(t)的褶积得到局部平面波分量s(L,pm,t).
(4)利用式(13)所示的逆倾斜叠加将所合成的平面波分量累加到地震记录d(rd,rs,t)中,待所有射线束中心处理完成后,即可得到最终的模拟炮记录.
1.4 KBTM算子
对式(6)所示的KTM算子应用类似的走时近似和加窗单位分解算法,可以得到如下的KBTM算子:
+T(L)),
(16)
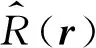
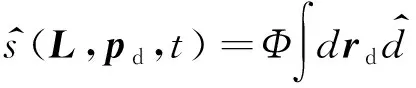
(17)
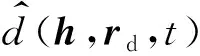
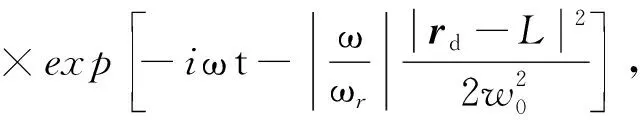
(18)
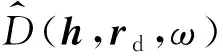
KBTM的单炮偏移计算过程可以简要概括为:
(1)沿射线束中心循环,并在不同的射线束中心处利用式(17)和式(18)将单炮地震记录分解为局部平面波分量.
(2)对于每一个成像点,求取由震源经地下成像点到射线束中心的双程地震波走时和接收点射线参数等信息,根据式(16)拾取平面波振幅并累加到成像点上.
(3)重复步骤(1)和(2),待所有射线束中心处理完成后,即可得到单炮成像结果.
2 模型及实际资料试算
本节首先应用Marmousi模型进行LSKTM和LSKBTM的测试,证明两者具有非常接近的成像精度,并验证LSKBTM在计算效率上的优势.接下来,应用二维和三维探区地震数据测试LSKBTM的实际应用效果.
2.1 Marmousi模型
首先,将Marmousi模型的层速度场通过Dix公式转换为图1a所示的均方根速度场,为便于后续的成像对比,在此直接将层速度场计算得到反射率剖面作为时间域反射率(图1b);然后,将时间域均方根速度和反射率作为输入数据,利用KFM计算了200炮地震记录(部分炮记录如图2所示),炮间隔为40 m,每炮接收地震道数为151,道间距为20 m,震源信号为主频20Hz的雷克子波.
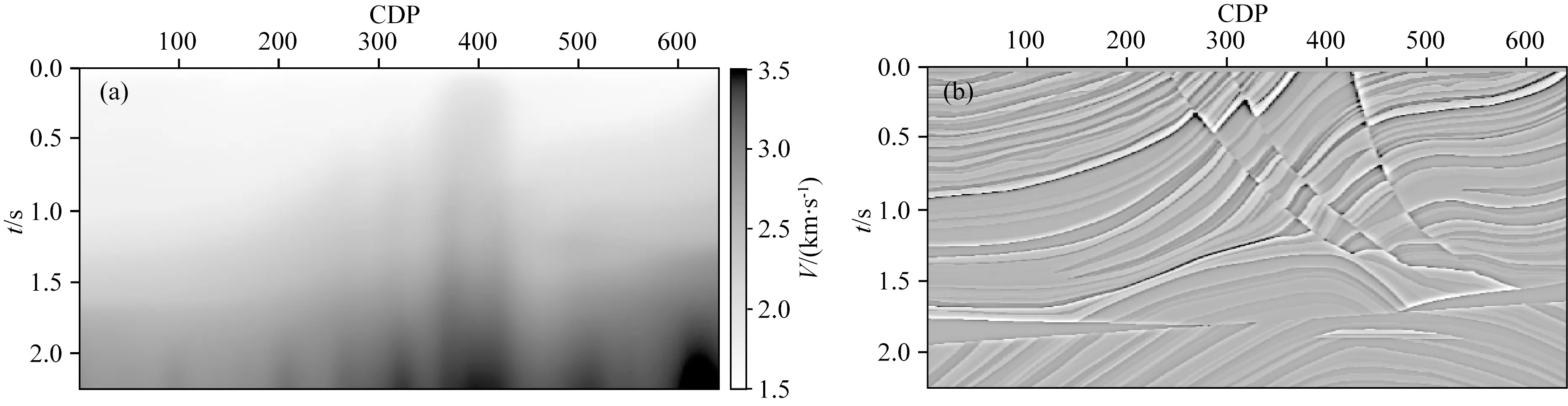
图1 时间域Marmousi模型 (a) 均方根速度场; (b) 时间域反射率剖面.Fig.1 Marmousi model in time domain(a) RMS velocity field; (b) Reflectivity profile.
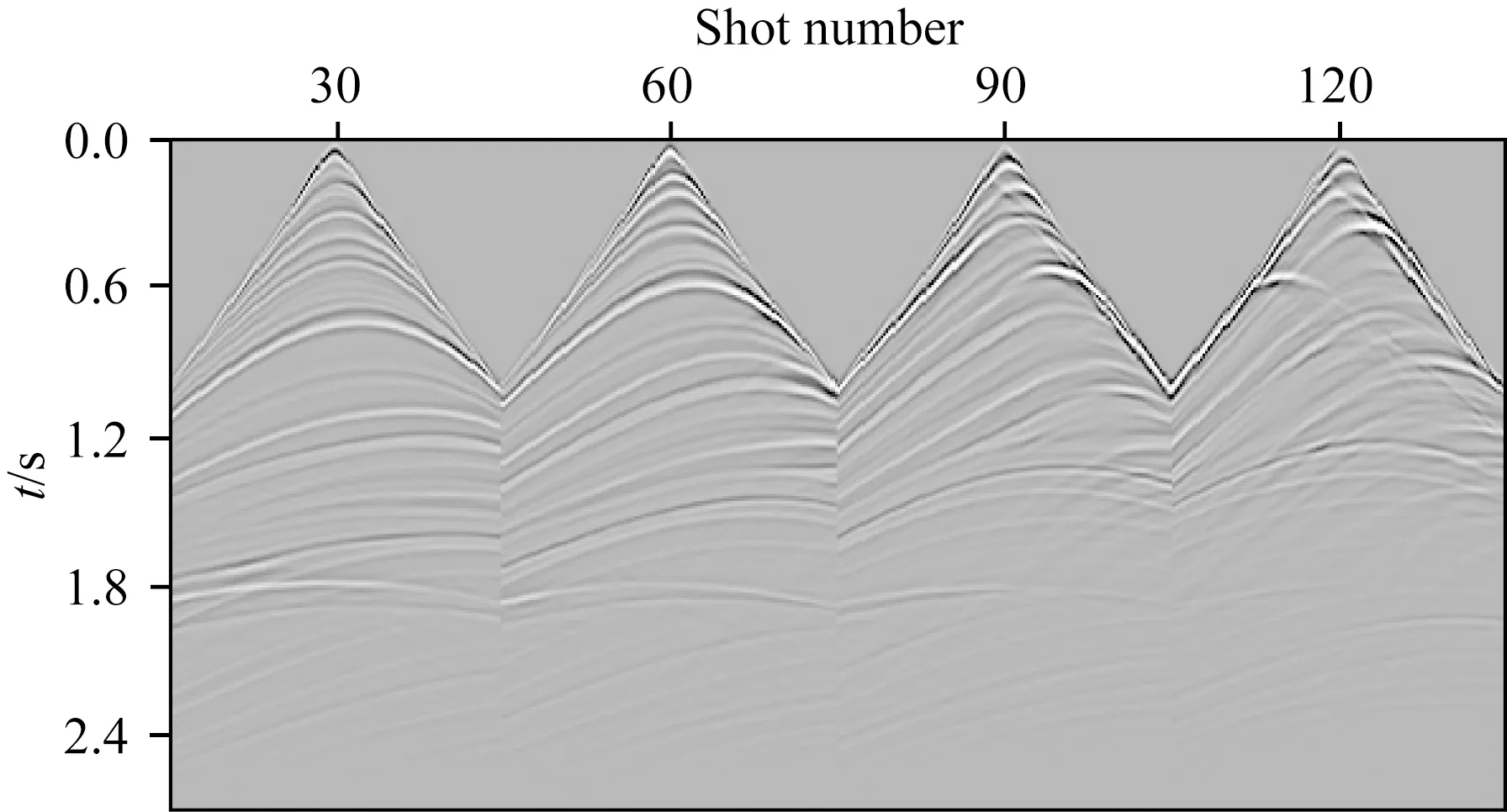
图2 不同位置处的KFM单炮记录Fig.2 Single-shot gathers using KFM at different source locations
分别使用LSKTM和LSKBTM(初始束宽度设为240 m)对模拟记录进行偏移处理,经过1次迭代得到的KTM和KBTM结果分别如图3a和图3b所示,图4同时展示了两者在CDP=420处的成像波形同真实反射率的叠合对比(KTM蓝色,KBTM绿色,真实反射率黑色).可以看到KTM和KBTM均较好的恢复了地下的构造信息,成像效果非常接近.但由于KTM和KBTM只是正演过程的共轭转置,同图1b所示的真实反射率相比,其成像分辨率较低,成像振幅也不准确.经过12次迭代后的LSKTM和LSKBTM结果分别如图5a和图5b所示,相应的成像波形对比结果如图6所示,可以看到两种LSM方法的成像结果几乎完全相同,均较好的恢复了地下真实的反射率信息,成像分辨率和照明度较常规偏移结果有了大幅度改善.由图7所示的反演收敛曲线对比可以看出,两种方法也具备相似的收敛速度.使用相同的计算节点对比两种方法的计算时间,其中,LSKTM的总计算时间为361.9 s,LSKBTM的计算时间为64.1 s,因此LSKBTM相对于常规LSKTM的加速比约为5.7,也就是说,LSKBTM仅需要约4次常规KTM的计算量即可完成12次LSKBTM的迭代运算.
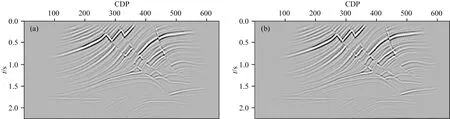
图3 常规偏移成像剖面对比(a) KTM成像结果; (b) KBTM成像结果.Fig.3 Comparison of migrated images(a) KTM image; (b) KBTM image.
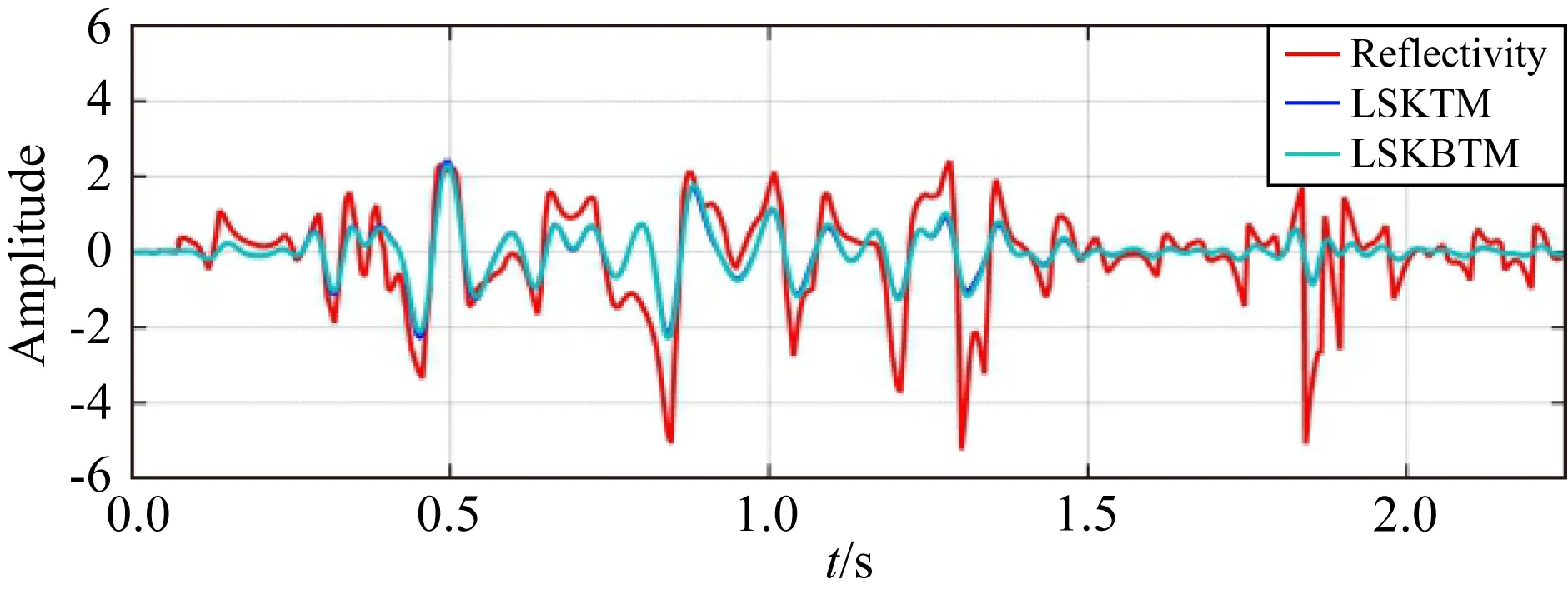
图4 CDP=420处成像波形对比其中红色曲线代表真实反射率,蓝色曲线代表KTM,绿色曲线代表KBTM.Fig.4 Comparison of waveforms at CDP=420Red curve is true reflectivity. Blue curve is KTM. Green curve is KBTM image.
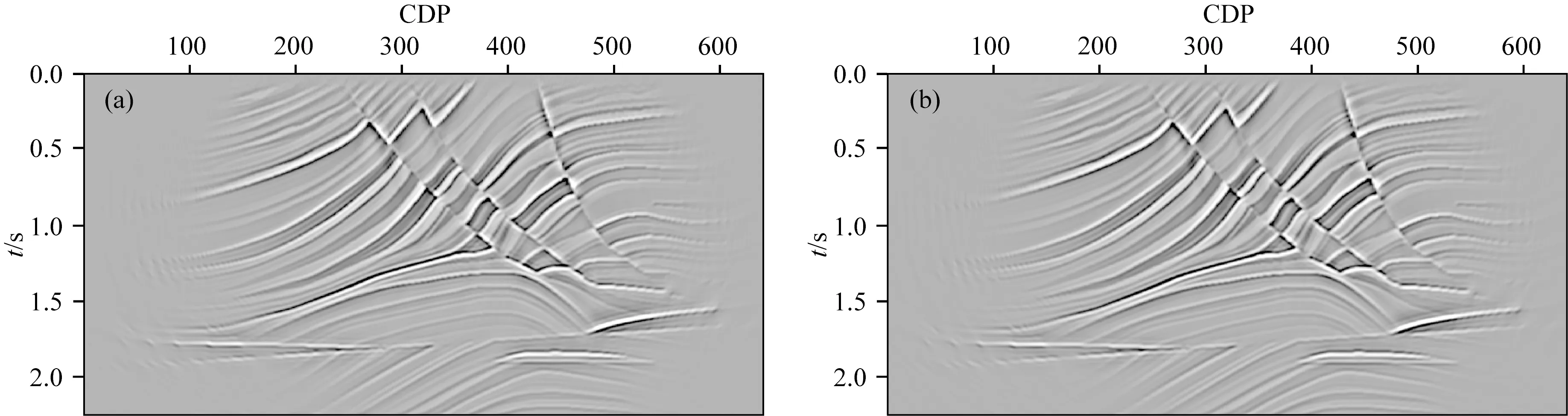
图5 最小二乘偏移成像剖面对比(a) LSKTM成像剖面; (b) LSKBTM成像剖面.Fig.5 Comparison of least-squares migration images(a) LSKTM image; (b) LSKBTM image.
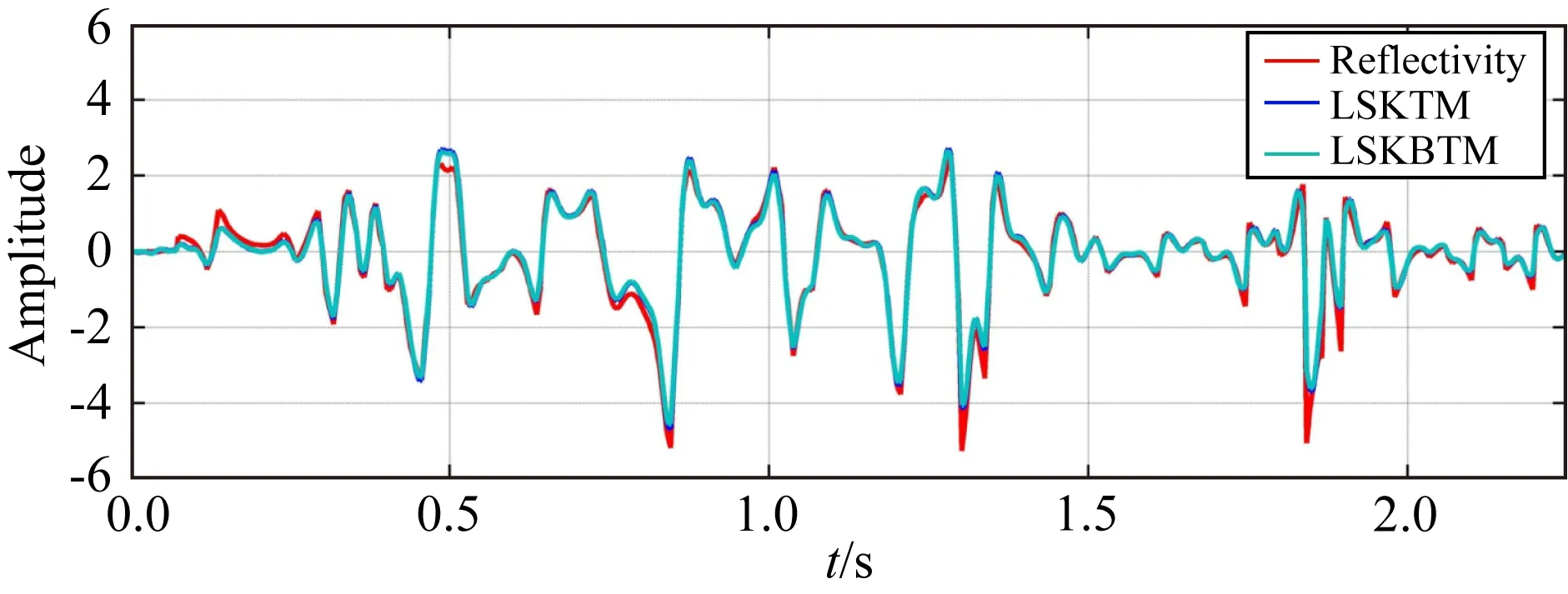
图6 CDP=420处成像波形对比其中红色曲线代表真实反射率,蓝色曲线代表LSKTM,绿色曲线代表LSKBTM.Fig.6 Comparison of waveforms at CDP=420Red is true reflectivity, blue is LSKTM image, and green is LSKBTM image.
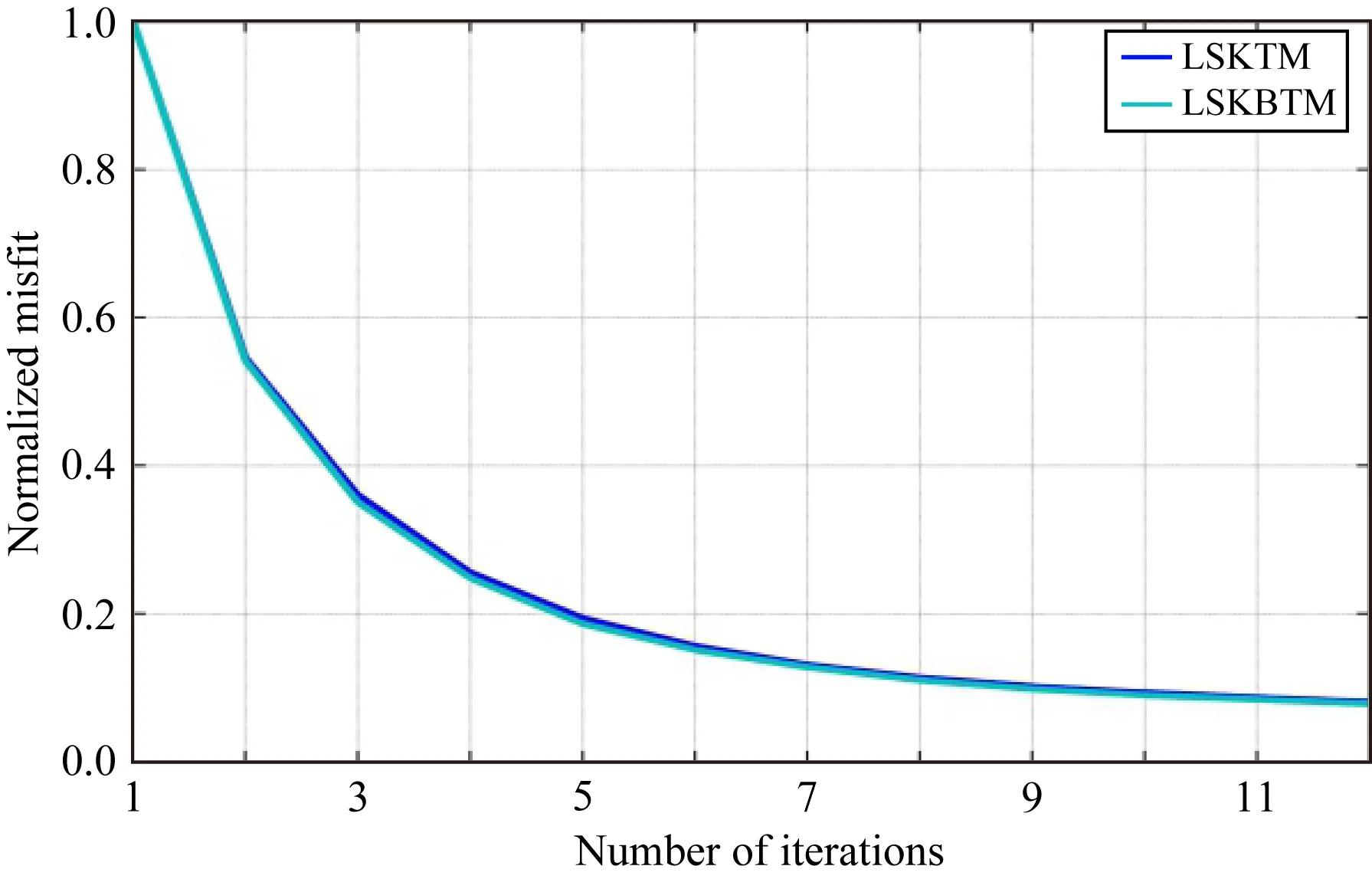
图7 归一化目标函数收敛曲线其中蓝色曲线代表LSKTM,绿色曲线代表LSKBTM.Fig.7 Normalized misfits versus number of iterationsBlue is LSKTM, and green is LSKBTM.
2.2 二维实际数据
使用某二维探区实际地震数据进行LSKBTM的测试,图8展示了时间域偏移速度分析后得到的均方根速度场.该数据共有220炮,每炮271道,炮间隔为40 m,道间距为20 m,其中第100炮接收记录如图9a所示.测试使用的震源信号为主频为20 Hz的雷克子波,选择的束初始宽度为240 m.

图8 均方根速度场Fig.8 RMS velocity field
应用LSKBTM对数据进行了10次迭代成像运算,对应的数据残差得到了较好的收敛(降低约83%).经过1次(KBTM)和10次LSKBTM反演迭代后的成像结果分别如图9和图10所示,可以看到,同KBTM相比,LSKBTM大幅提升了成像层位的分辨率和连续性.图11进一步对比了两者的成像频谱,可以看到同KBTM相比,LSKBTM有效拓宽了成像剖面的频带范围.KBTM的成像效果同常规KTM近乎效同(未展示),但计算时间仅为KTM的1/6,因此在本例中,LSKBTM相对于LSKTM的加速比约为6.

图9 KBTM成像结果Fig.9 Imaging result using KBTM

图10 LSKBTM成像结果Fig.10 Imaging result using LSKBTM
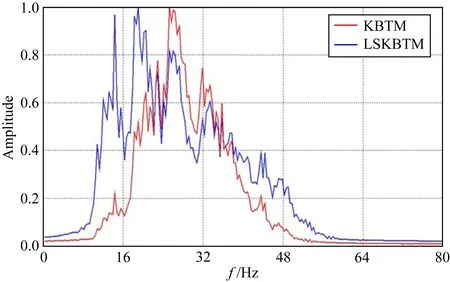
图11 成像频谱对比Fig.11 Spectrum comparison between KBTM and LSKBTM
2.3 三维实际数据
使用某三维探区实际地震数据进行LSKBTM的测试,图12展示了时间域偏移速度分析后得到的均方根速度场.应用LSKBTM对数据进行了10次迭代成像运算,其中经过1次迭代的KBTM结果和10次迭代的LSKBTM结果分别如图13和图14所示,可以看到同KBTM偏移剖面相比,LSKBTM大幅提升了成像的分辨率,时间切片中展示的地质构造更加的清晰聚焦.图15进一步对比了两个成像剖面的频谱(单位为dB),可以看到同KBTM(红色曲线)相比,LSKBTM(蓝色曲线)不但大幅度提高了成像结果的主频,有效频带宽度也得到大幅度拓宽.由于三维炮记录在crossline方向的采样稀疏(200 m),本例仅在inline方向(采样间隔20 m)进行了平面波的合成和分解(束中心间隔为200 m),同常规LSKTM相比,LSKBTM的加速比为5.3.
图12 均方根速度场Fig.12 3D view of RMS velocity field

图13 KBTM成像结果Fig.13 Image result of KBTM
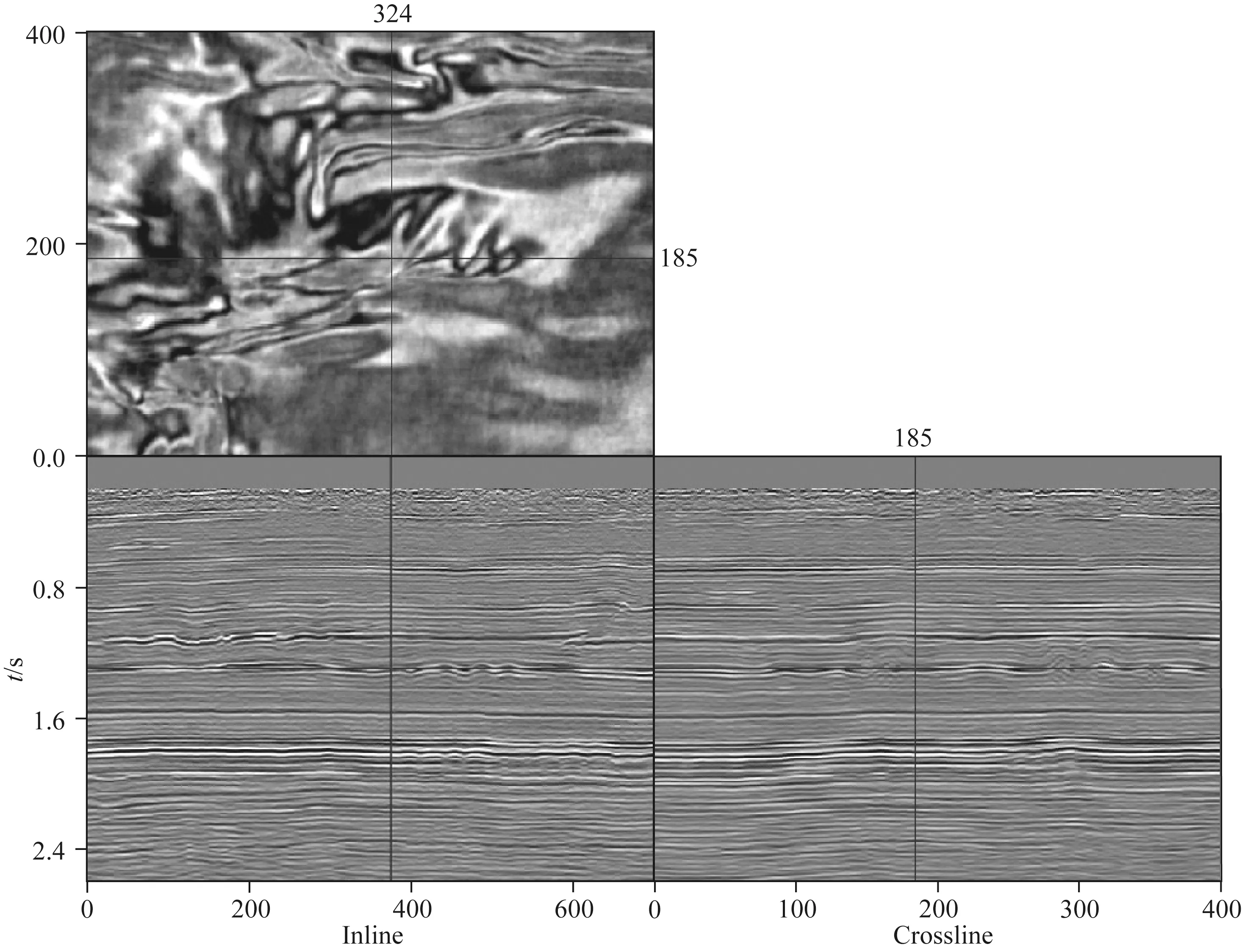
图14 LSKBTM成像结果Fig.14 Image result of LSKBTM
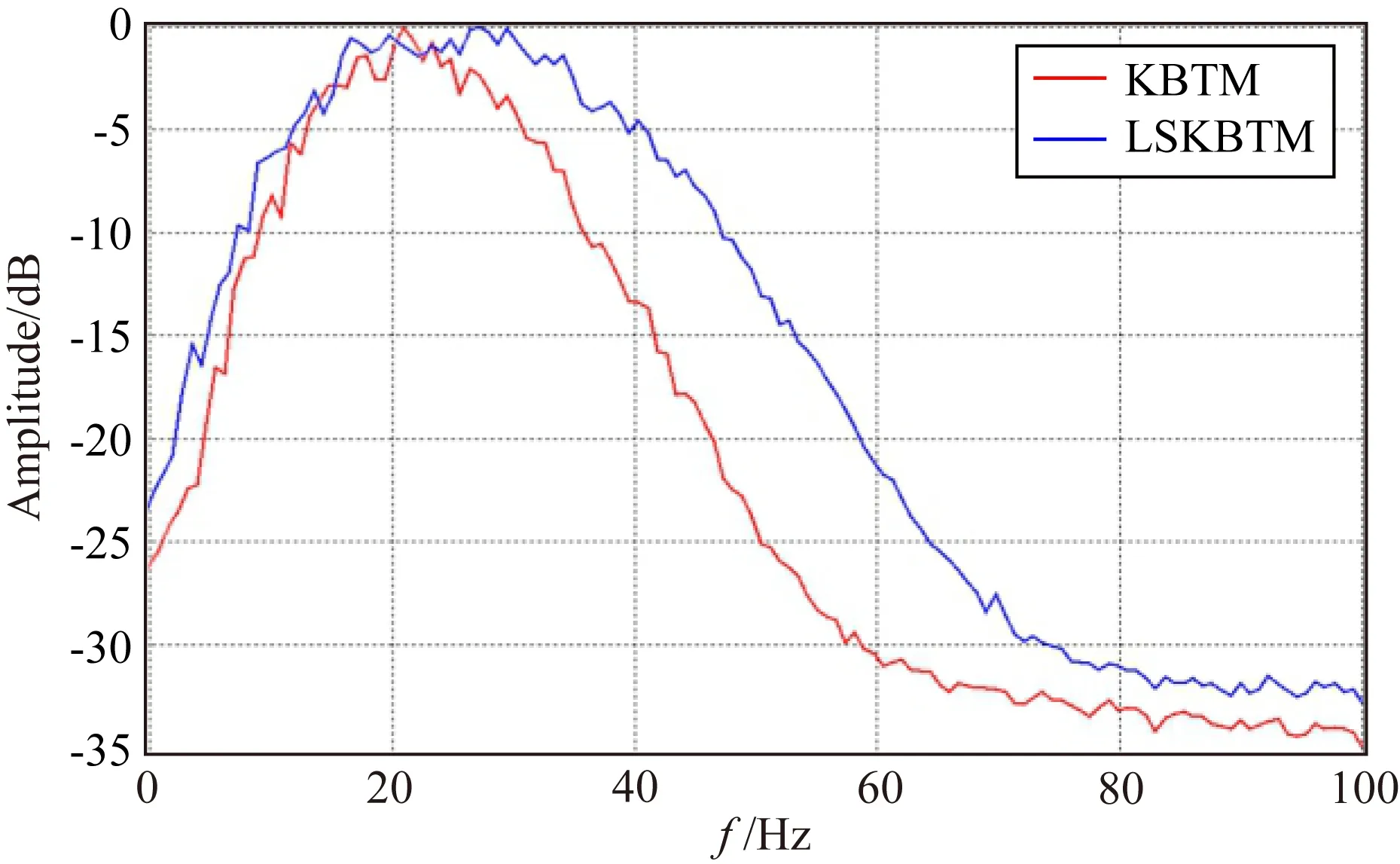
图15 KBTM(蓝色曲线)和LSKBTM(红色曲线)的成像频谱对比Fig.15 Spectrum comparison between KBTM (blue) and LSKBTM (red)
3 结论
本文基于地震数据的局部平面波分解/合成策略,在时间域KFM/KTM的基础上,实现了高效的KBFM/KBTM算子,并以此为基础发展了快速的LSKBTM方法.同常规LSKTM相比,LSKBTM不但具备相当的反演成像精度和迭代收敛速度,还大幅度降低了计算成本.不同于深度域的束偏移方法,本文方法中平面波的合成/分解仅与成像点的速度有关,因此其对偏移速度的敏感性同常规时间偏移完全相同.虽然本文是通过常规直射线走时算法进行推导,但很容易引入弯曲射线、各向异性等因素来提高走时计算精度.此外,本文方法还可以发展为共炮检距算法,从而利用地震数据在炮点方向的冗余度进一步提高计算效率.
