基于Marchenko理论压制自由表面多次波方法研究
2021-05-07王小卫王孝谢俊法曾华会赵玉合
王小卫, 王孝, 谢俊法, 曾华会, 赵玉合
中国石油勘探开发研究院西北分院, 兰州 730020
0 引言
对于深海地震数据,自由表面多次波衰减是地震资料处理过程中的重点和难点.多次波的存在,特别是与水层相关多次波的存在常常会对接收到的有效波产生破坏,对地下地质构造成像、速度分析的准确性等环节造成影响(牛滨华等, 2002;路鹏飞等,2020;王常波等,2020).
预测反褶积方法是早期地震资料处理中压制短周期多次波和海上鸣震的有效处理方法(Robinson, 1957),但是对于地下介质构造较为复杂的地区,预测反褶积对海上鸣震等短周期多次波压制效果较差.Kennet(1979)提出了反馈迭代法,Berkhout(1982)进一步对反馈迭代法进行了方法改进,使其适用于任何表面多次波模型.表面相关多次波去除方法(SRME)方法基于反馈迭代模型,在无需已知地下介质信息前提下利用地震数据本身预测多次波,是当前工业上成熟应用的多次波压制技术(Verschuur, 1991; Verschuur et al., 1992; Berkhout and Verschuur, 1997; 王维红等, 2007; 李学聪等, 2010; 石颖和王维红, 2012; 石颖等, 2013; 徐嘉亮等,2018).对于近炮检距缺失的地震资料,使用SRME方法需要对缺失数据进行波场外推来获得,数据重构过程中将会产生一定误差,影响表面多次波的压制结果.Moore和Bisley(2006)、Martin等(2011)利用模型驱动方法压制自由表面多次波,基于模型的自由表面多次波压制方法在部分短周期多次波压制方面取得了较好的效果,但是对地震数据之外的信息依赖程度过高(赵昌垒等, 2013).基于稀疏反演的一次波估计方法EPSI(Estimation of Primaries by Sparse Inversion)是建立在与SRME相同的理论基础上,通过直接估计一次波脉冲响应和地震子波,进而重构出一次波和自由表面多次波,避免了自适应相减步骤,更好地保护了有效信号(Van Groenestijn and Verschuur, 2009a,b).但是该方法是一种迭代反演方法,在迭代反演过程中存在计算量较大的问题,同时该方法计算时忽略震源的方向特性,假设所有炮具有相同的震源子波,这在实际数据中并不一定时时满足,进而影响预测效果.
基于Marchenko理论压制多次波方法,主要利用地下介质中虚源点的格林函数和地表得到的反射响应进行多次波预测.Broggini和Snieder(2012)将该方法引入地球物理领域.其本质是通过虚源点与地表之间的直达波记录和地表反射响应反演得到上下行格林函数.Broggini等(2012)、Wapenaar等(2013)将该方法扩展到二维和三维.Marchenko方法输入数据不包含自由表面多次波,因此计算得到的格林函数也不包含与自由表面相关的多次波.本文对Marchenko方程进行了改进,在自由表面多次波存在的情况下得到格林函数场,得到包含一次波、层间多次波和自由表面多次波的格林函数.该方法能够预测关于海水面的自由表面多次波,进而利用自适应匹配滤波方法使自由表面多次波得到有效压制.
1 方法原理
Marchenko方法实质上是通过虚源点与地表之间的直达波记录和地表反射响应反演得到格林函数的上下行波场.本文引入一个假想介质,假想介质中的波场如图1a所示,实际介质中波场如图1b所示.图1a中,在Di深度以下为均匀半空间的假想介质,引入聚焦函数f1,f1在Di深度以下无反射.在实际介质和假想介质中,表面边界D0以上无反射.Wapenaar等(2014)将实际介质的上行和下行格林函数与地表的反射响应联系起来得到:
×R0(x″0,x0,ω)dx,
(1)
×R0(x″0,x0,ω)dx,
(2)
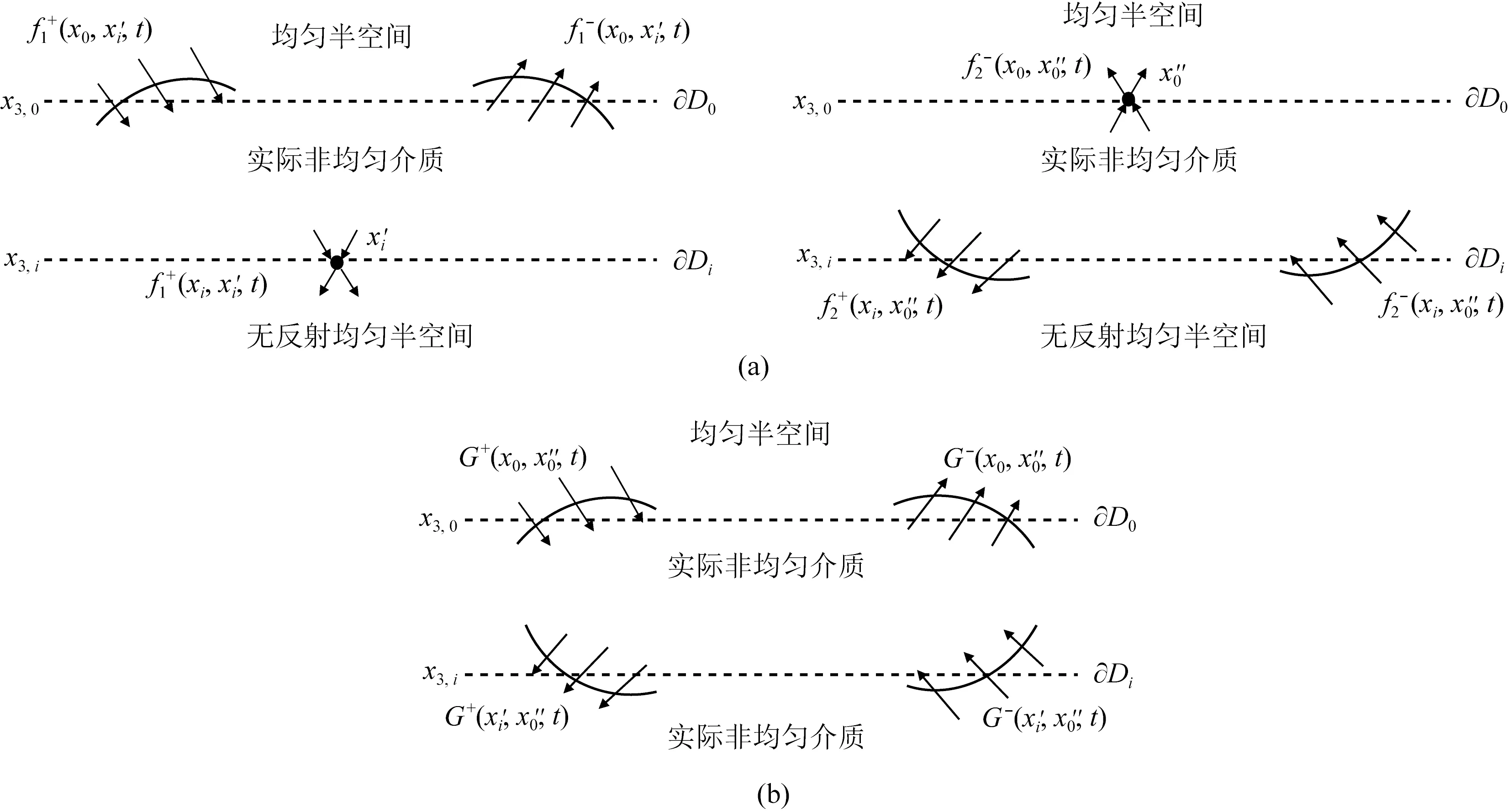
图1 假想介质中波场(a)和实际介质中波场(b)传播情况Fig.1 Wave field propagation in imaginary medium (a) and real medium (b)
其中,G0表示实际介质中的格林函数,R0表示地表反射响应,反射响应R0不包含与自由表面相关的多次波.在本文中上标“+”表示下行波场,上标“-”表示上行波场.对方程(1)、(2)求和,并利用炮点-检波点互易关系对格林函数求解:
G0(x″0,x′i,ω)=f2(x′i,x″0,ω)*
(3)
聚焦函数f2定义为:
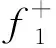
(4)
在地震波直接到达聚焦点之前没有能量到达,因此格林函数上下行波场为0,将其作为迭代方法的初始条件,将聚焦点作为虚源点,对虚源点直接到达检波点的记录进行时间反转作为聚焦函数下行波场的初始值,构成迭代方案的基础完成迭代更新.
在介绍由包含自由表面多次波情况下的反射响应得到格林函数之前,本文先引入R、R0、G、G0的概念,R为自由表面存在时记录的反射波,R0为无自由表面介质的反射响应.G为存在自由表面时位于介质中某一点的虚源点在表面上的格林函数,G0是不存在自由表面时的格林函数.Marchenko方法为不存在自由表面的情况下聚焦波场的理论.也就是说,从R0中求得格林函数G0(Rose, 2002; Broggini et al., 2012; Wapenaar et al., 2013).
Wapenaar等(2004)提出将存在和不存在自由表面的介质传播算子联系起来,从而通过G0计算出G(自由曲面存在时的格林函数),其频域表达式为:
×R(x0,x″0,ω)dx,
(5)
其中,D0为采集面,x0和x′i为沿D0和Di(D0以下的任意深度平面)的空间位置,R为D0界面处下行入射波场的反射响应.在该方法中,本文将传输响应替换为相应的格林函数G或G0,因为格林函数是从聚焦点到表面的总传输波场.需要注意的是,这种方法遵循由R进行SRME得到R0,进而获得G0,最后得到G的环节.然而,本文可以直接从测量的反射数据R通过计算得到自由表面存在时的格林函数G,即:直接由反射数据R求取格林函数,避免了SRME和G0的求取.本文将Marchenko方法由R0求取G0的公式推广到包含自由表面多次波(由R求G).来自自由表面的反射包含在聚焦方法中,类似于Wapenaar等(2004)对自由表面多次波的处理.
本文定义水平和深度空间坐标,如:x0=(xH,x3,0)、xH表示在深度x3,0处水平坐标(x1,x2).本文定义了波动方程在介质中聚焦于一点的解,本文称之为聚焦函数f1和f2.f1函数所涉及的波在x′i处聚焦在一个定义的深度水平(∂Di)上,对于在采集表面(∂D0)上x0的入射波和传出波,f2函数是一个对于入射波和传出波在∂Di上且在D0上聚焦的波的解,如图1a.
在∂D0以上带有自由表面的实际非均匀模型,如图2所示.与Wapenaar等(2013)中没有自由表面的模型不同,本文认为来自自由表面的反射是下行源,类似于Wapenaar等(2004)的研究.在图2中,本文描述了波场中的上行和下行分量.在∂D0上的波场的下行分量为G+(x0,x″0,ω)=δ(xH-x″H)+rR(x0,x″0,ω),等号右边包含了下行的脉冲源和自由表面的反射.下行脉冲源δ(xH-x″H)是一个2D狄拉克δ函数,x″H为聚焦函数f2的聚焦点横坐标.
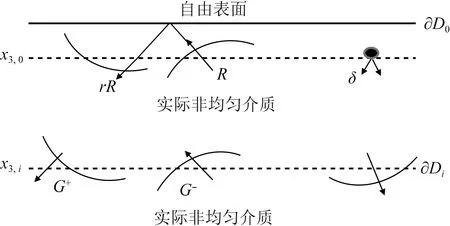
图2 实际非均匀介质中自由表面存在时的波场Fig.2 Wave field in real inhomogeneous medium with free surface
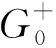
分别将聚焦函数(f1和f2)之间的波场和聚焦函数与实际介质之间的波场联系起来.那么,自由表面存在时对应的格林函数与聚焦函数f2具有关系式为:
G(x′i,x″0,ω)=f2(x′i,x″0,ω)*
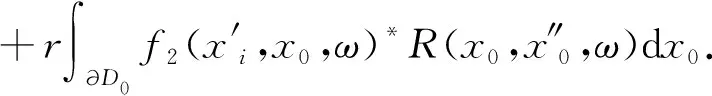
(6)
对比方程(6)和方程(3),方程(6)右边的最后一项表示从自由表面反射的波场信息.方程(6)中的反射响应R包含自由表面的反射波,而表达式(3)包含的是没有自由表面介质的反射响应R0.其中,上行格林函数和下行格林函数表达式分别如式(7)和式(8)所示:
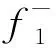
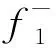
(7)
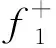
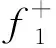
(8)
对式(7)、(8)计算得到下行格林函数进行去直达波处理,将地下虚源点与地表接收点之间去直达波后的格林函数下行波场和完整的上行波场做褶积,预测出与自由表面相关的多次波:
(9)
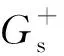
2 模型测试
2.1 模型测试一
本文利用三层水平层状速度模型如(图3)所示验证本文提出方法的正确性.速度模型大小为2000 m×2500 m,水平方向有200个网格点,垂直方向上有250个网格点,网格间距均为10 m.共放201炮,每炮有201个检波点接收,炮检距和检波点间距为10 m.所用震源子波为主频25 Hz的雷克子波,反射时间记录长度为3.5 s,采样间隔为1 ms.第一个和最后一个震源位置分别位于模型起始处.构造上下行格林函数的虚源点均匀分布于速度模型第一层的400 m处和第二层的1200 m处,点间距为10 m,如图3中的红点所示.
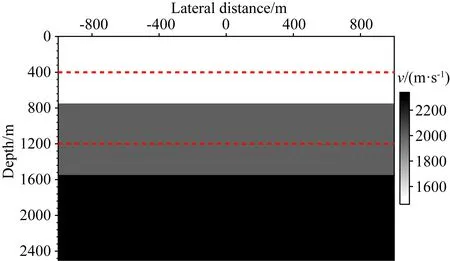
图3 速度模型Fig.3 Velocity model
图4a为正演的第100炮地震记录,图4b为利用Marchenko方法预测的自由表面多次波,图4c为地震记录压制自由表面多次波的数据.从图4中可知Marchenko方法预测的表面多次波在走时上与实际的表面多次波有很好的一致性,振幅和频率略有差异,该差异可由多道匹配自适应相减方法来消除.如图4c所示,经过自适应匹配相减后,正演地震记录中自由表面多次波得到有效压制(红色箭头所指),从而说明利用本文提出的基于Marchenko自由表面多次波压制方法可有效压制自由表面多次波.
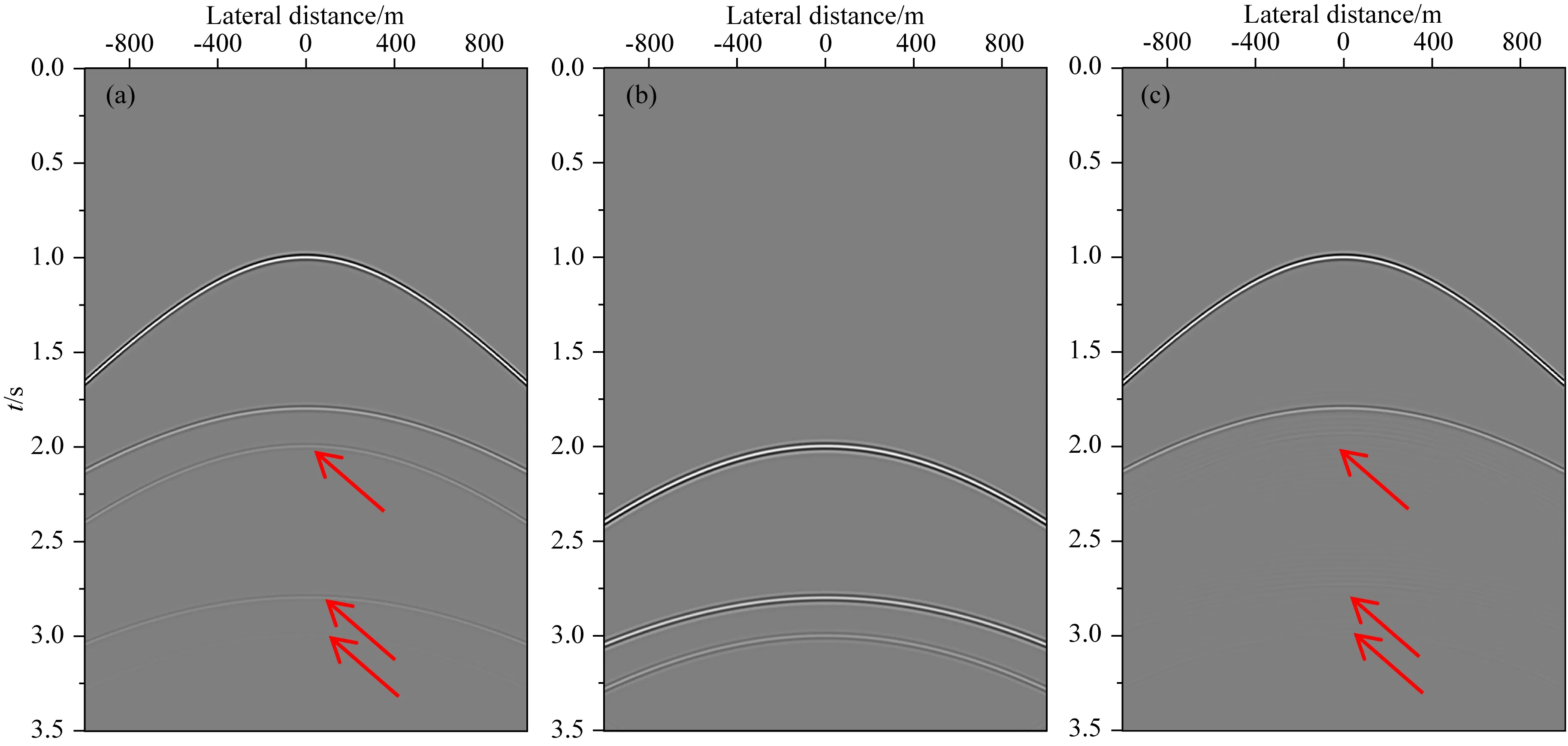
图4 第100炮地震记录(a) 多次波压制前; (b) 预测的多次波; (c) 多次波压制后.Fig.4 Seismic record of the 100th shot(a) Before multiple suppression; (b) Predicted multiples; (c) After multiple suppression.
2.2 模型测试二
为了验证该方法的有效性,本文在测试水平模型后对SMARRT模型进行测试.SMARRT模型正演参数为:震源和检波点都位于海水面,采样时间间隔为0.008 s,记录长度为5 s,共1387炮,每炮361道,炮间距为75 m,模型左右下界面采用吸收边界.图5为SMARRT速度模型,红点为虚源点位置.

图5 SMARRT速度模型Fig.5 SMARRT velocity model
图6为利用Marchenko自由表面多次波压制方法压制多次波前后单炮对比图,图6a为炮号4500的原始炮集,图6b为预测的多次波,图6c为压制多次波后的地震记录.从图中可以看到基于Marchenko自由表面多次波压制方法可以有效压制表面多次波(红色箭头所指)而无损有效信号,提高了地震资料的信噪比.
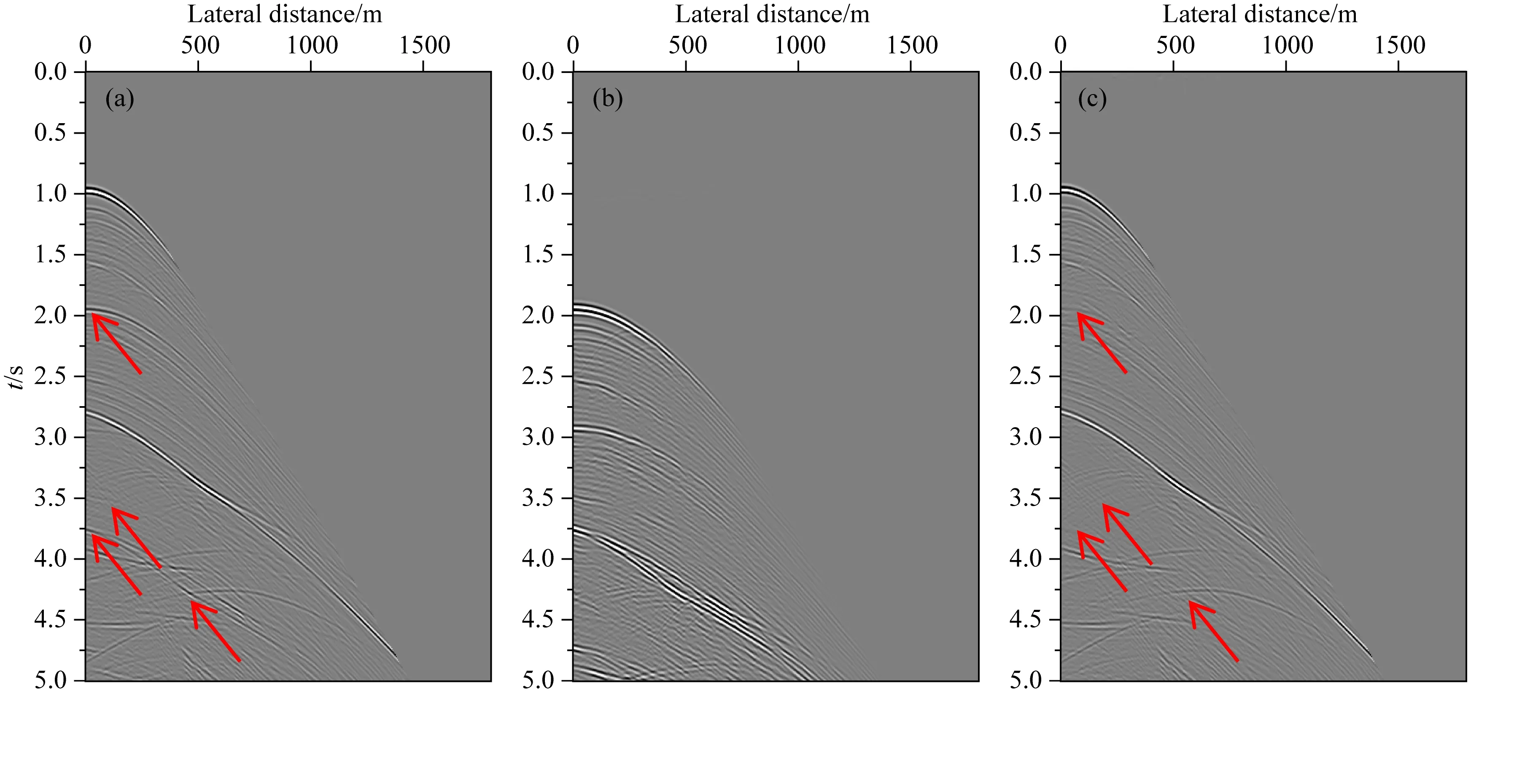
图6 Marchenko方法多次波压制前后单炮记录(a) 多次波压制前; (b) 预测的多次波; (c) 多次波压制后.Fig.6 Single shot record before and after multiple suppression by Marchenko method(a) Before multiple suppression; (b) Predicted multiples; (c) After multiple suppression.
图7为利用Marchenko自由表面多次波压制方法压制多次波前后抽取的零偏移距剖面对比图,图7a为原始地震剖面,图7b为预测的多次波数据剖面,图7c为压制多次波后的地震剖面.从图中可以看到自由表面多次波得到有效压制(如红色箭头和矩形框内所示).由该实例说明基于Marchenko自由表面多次波压制方法对于复杂模型具有较强的适应性,通过进一步研究有望应用于实际数据.
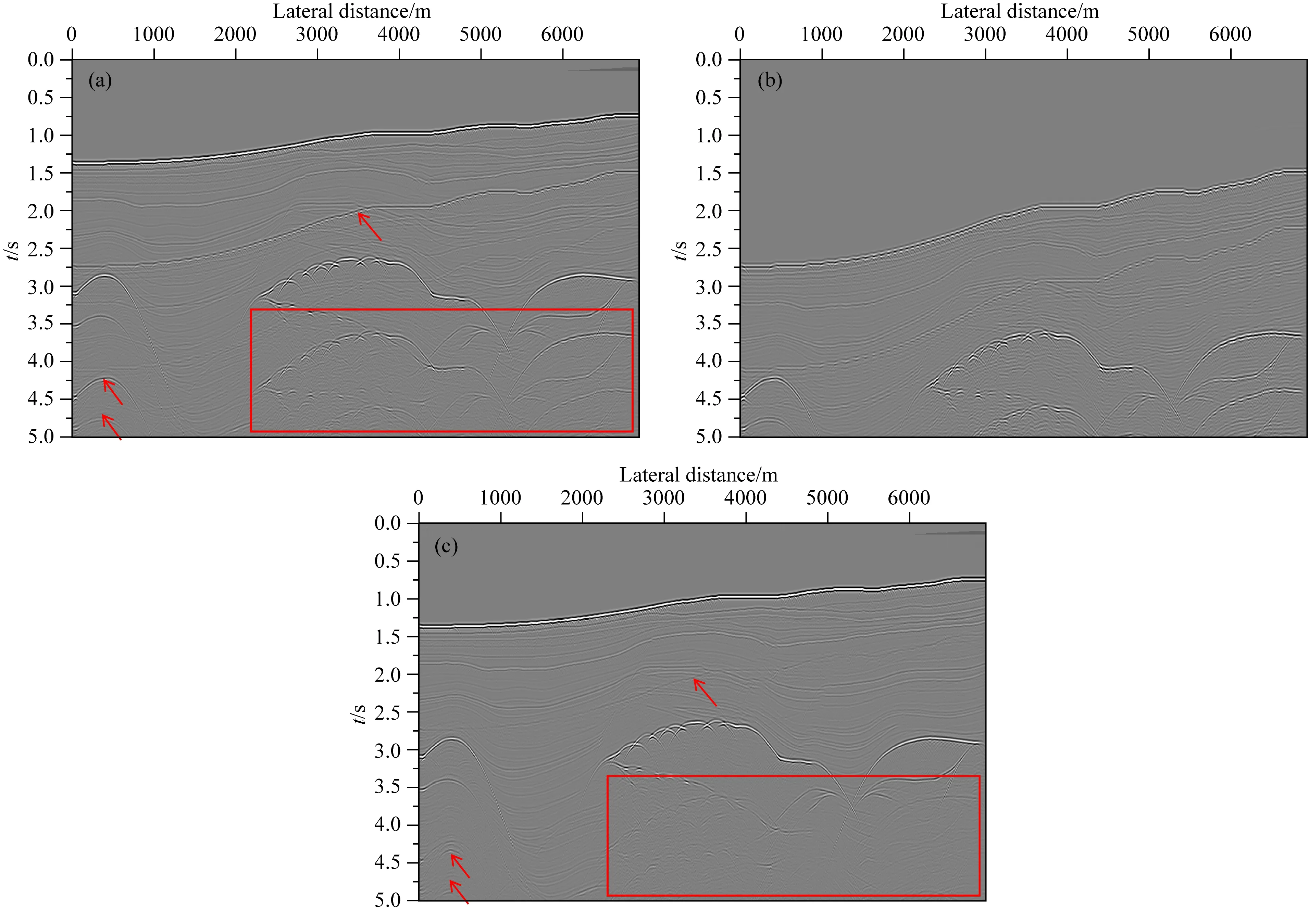
图7 Marchenko方法多次波压制前后零偏移距剖面(a) 多次波压制前; (b) 预测的多次波; (c) 多次波压制后.Fig.7 Zero offset profile before and after multiple suppression by Marchenko method(a) Before multiple suppression; (b)Predicted multiples; (c) After multiple suppression.
3 结论
本文提出一种改进的自聚焦Marchenko多次波压制方法,该方法不需要去除海水面相关的自由表面多次波,同时能够对自由表面多次波进行压制.传统压制自由表面多次波方法(如SRME)需要对近道缺失的地震数据进行补充,同时不能压制地下强阻抗界面的层间多次波;压制层间多次波方法也都需要先验地下模型,计算效率有待提高.本文提出的方法能够改善上述方法的缺陷,不需要对近道数据进行补充,也不需要地下构造的速度模型,仅仅需要背景速度场及迭代更新策略就可以使目标函数得到收敛.由模型测试证明本文提出的方法是有效可行的,该方法能够对自由表面多次波进行有效压制.
本文方法在构建的上下行格林函数场中,同时包括自由表面多次波和层间多次波,下一步利用复杂介质模型测试本文方法对同时压制自由表面多次波和层间多次波的有效性,该方法有望在实际海洋数据当中得到广泛应用.
