底辟热流体上涌的数值模拟及其对早古生代青藏高原柴北缘祁连弧形成的启示
2021-05-07原一哲胡才博魏东平
原一哲, 胡才博* , 魏东平
1 中国科学院大学地球与行星科学学院, 北京 100049 2 中国科学院计算地球动力学重点实验室, 北京 100049
0 引言
超高压变质岩是研究固体地球不同圈层地球动力学过程的重要依据,历来受到地质科学家的高度重视.中央超高压变质带规模是世界之最,位于我国中部,东起苏鲁地区,西至阿尔金,全长4000多千米,是研究超高压变质岩形成过程的天然实验室.超高压变质岩石是如何从地下90 km左右的深度折返至地壳浅层并最终出露地表,在科学界至今还没有统一的认识.柴达木北缘超高压变质带和南祁连造山带是距今520~400 Ma由古特提斯洋持续南向俯冲引起的.有学者认为青藏高原北部柴达木北缘超高压变质带是由于海洋俯冲过程中底辟流和角流上升过程中的变质岩形成的(Lardeaux et al., 2001;Yin et al., 2012).现今地质勘察表明,柴达木北缘超高压变质体在时间和空间上重叠了早期古生代祁连岩浆弧变质带.
目前,主要有两种俯冲构造模型描述超高压变质岩的形成过程:(1)喜马拉雅陆陆碰撞模型(Liou et al., 2004),强调在陆-陆碰撞中引起的超高压变质作用,超高压变质地体应该位于俯冲板块的被动大陆边缘(O′Brien et al., 2001),碰撞下行的大陆岩石层地质年代学和地球化学特征留存于向上运移的超高压变质岩石(Jahn, 1999);(2)安第斯洋陆俯冲模型(Mancktelow, 1995; Dobretsov, 2000),即由于大洋俯冲和弧形岩浆形成的超高压变质作用.根据前人的研究,祁连弧超高压变质岩的形成可能由安第斯洋陆俯冲模型来解释,但岩浆上涌时空演化的细节仍需进一步研究.
超高压变质岩石往往随着海洋板块俯冲被带入到大陆90 km以下深处,深俯冲的混杂岩可能转变为高密度的岩石,然后迅速折返至地壳浅部并部分出露地表.变质岩在上升过程中释放出来的水在浮力的作用下向上进入上覆热的地幔橄榄岩中,导致部分熔融.海洋板块俯冲导致热流体上涌存在两种模型,即管道流模型和底辟流模型,两者最主要的区别在于是否形成稳定的岩浆通道.图1a为管道流模型(Lardeaux et al., 2001 ),图1b为底辟流模型(Yin et al., 2012).本文仅研究底辟流模型,关于经典管道流模型详见(李忠海等,2015).
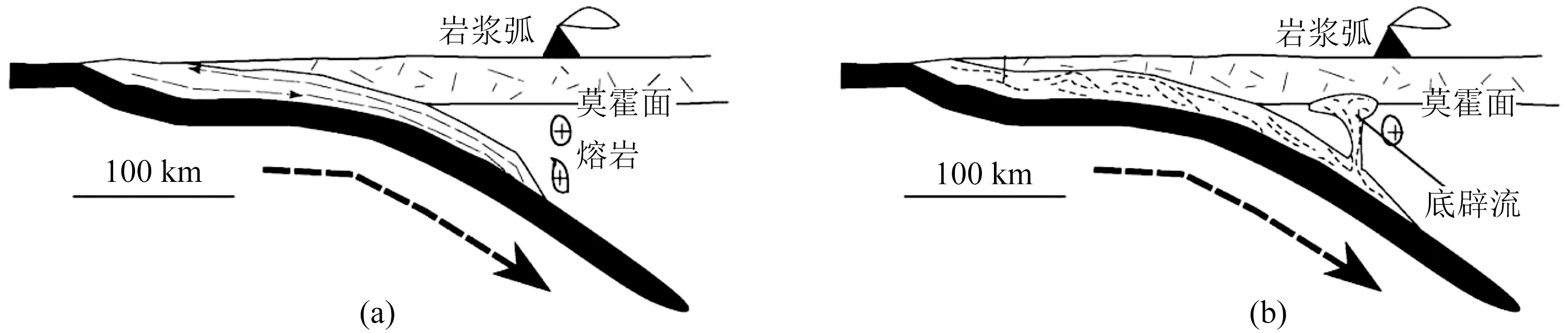
图1 两种海洋俯冲上涌模型(a) 海洋俯冲管道流模型(修改自Lardeaux et al., 2001); (b) 海洋俯冲底辟流模型(修改自Yin et al., 2012).Fig.1 Two types of ascent flow during oceanic subduction(a) Channel flow during oceanic subduction (Lardeaux et al., 2001); (b) Diapiric ascent and final emplacement during oceanic subduction (Yin et al., 2012).
很多的研究表明,柴达木北缘超高压变质带是早古生代祁连地体的一部分(Zhang et al., 1984; Hsü et al., 1995; Yin and Nie, 1996; Sengoer and Natal′in, 1996; Sobel and Arnaud, 1999; Gehrels et al., 2003a, 2003b).研究柴达木北缘超高压变质带可以深入认识古生代祁连地体的演化历史.总的来说,祁连山—南山地区包含三个元古宙被动大陆边缘地质构造带,即中央的大雪山构造带,北方的北祁连弧变质带,南方的北柴达木变质带(Gehrels et al., 2003a, 2003b; Song et al., 2005; Zhang et al., 2005).从空间分布来看,柴达木北缘早古生代岩浆弧变质体和北部柴达木地区超高压变质体有很好的一致性(Cowgill et al., 2003; Gehrels et al., 2003a, 2003b),暗示柴北缘超高压变质体的深部成因.
针对祁连地体发育过程,Yin等(2012)提出六阶段演化观点: (1) 900~600 Ma,昆仑—柴达木微板块边界被动大陆边缘发育; (2) 520~400 Ma,祁连海洋板块的南向俯冲和祁连弧形成,一个巨大的增生楔沿着昆仑—柴达木微板块的北缘不断向北发育; (3) 400~375 Ma,祁连弧覆盖在华北被动大陆边缘,以逆冲方式和华北板块碰撞;(4)230~100 Ma,从晚三叠纪到白垩纪产生弧后扩张盆地; (5) 50~40 Ma,印—欧板块碰撞,祁连山—南山地区构造缩短; (6) 40~0 Ma,华北克拉通的被动大陆边缘局部隆起造成新生祁连弧,与距今520~400 Ma以前早古生代祁连岩浆弧在空间上有重置现象.我们的研究主要关注祁连地体前三个阶段的地质演化过程,如图2所示.

图2 早古生代祁连地体和岩浆弧地质演化(Yin et al., 2012)(a) 阶段一(900~600 Ma),表示昆仑柴达木微板块两侧被动大陆边缘的发育; (b) 阶段二(520~400 Ma),表示祁连海洋板块的南向俯冲和祁连弧的发育; (c) 阶段三(400~375 Ma),表示祁连弧和华北大陆板块碰撞.Fig.2 Tectonic evolution of the early Paleozoic Qilian orogen and the magma arc(Yin et al., 2012)(a) Stage 1 (900~600 Ma): Development of passive continental margins on both sides of the Kunlun-Qaidam microcontinent; (b) Stage 2 (520~400 Ma): South-dipping subduction of the Qilian oceanic plate and development of the Qilian arc; (c) Stage 3 (400~375 Ma): Collision between the Qilian arc and North China.
过去几十年,随着计算机硬件的快速发展和高性能并行计算技术的不断提升,数值模拟方法成为理论解析解和物理模拟之外的地球动力学的重要方法,能够研究在复杂的几何、材料、边界条件之下地球介质在相对真实时空尺度的变形和流动.数值模拟研究主要包括两大类:简化模型和综合模型.简化模型只考虑简化的边界条件和几何模型,忽略板块运动中的很多关键物理参数,如不考虑相变问题,仅设定最简单的温度分布和边界速率等;综合模型能够更加真实地反映地球动力学过程,加入了很多物理、化学参数,比如复杂的流变学性质,温度和压力变化导致的岩石相变过程,可以模拟实时变化的温度、密度、黏度场等.底辟流上涌数值模拟难点主要体现在以下几个方面: (1) 要合理地模拟再现底辟上涌过程的各个阶段; (2) 各圈层之间巨大的黏滞度差异; (3) 自由表面的边界条件; (4) 复杂的岩体黏-弹-塑性本构关系(Hall et al., 2003); (5) 复杂的相变过程(Hebert et al., 2009); (6) 地幔内流体/熔体的迁移(Davies and Stevenson, 1992).
目前较为流行研究底辟流上涌过程的数值模拟算法有以下几种: (1) FEM-BEM:耦合了固体和流体两种算法(Morra et al., 2006),地幔黏性流体区域使用了边界元算法(BEM)中的格林函数;将岩石圈和平板变形视为固体材料,使用有限元法(FEM)进行计算.(2)Underworld:一种流体动力学方法,使用标准Euler有限元网格离散化模型,并采用拉格朗日粒子表示不同的材料(Moresi et al., 2007).(3)E-Script:运用“水平集”的数值方法(Gross et al., 2007),该方法常常用于追踪物体界面及形状,离散模型则使用有限单元网格.(4)FDCON:一种有限差分算法.将动量方程和质量守恒方程改写为与黏滞度和流线方程相关的双调和方程(Schmeling and Marquart, 1991),用Kolesky分解法直接求解.(5)LAPEX-2D:该算法使用网格-粒子方法(Sulsky et al., 1995)和显式拉格朗日有限差分技术(Babeyko et al., 2002)求解质量、动量和能量平衡方程,适用于求解黏弹性问题.(6)CITCOM:一种有限元算法(Moresi and Solomatov, 1995).有限单元是以恒定压力和线性速度为特征的双线型四边形.每个单元都进行属性内插并且直接应用于积分点.(7)I2VIS:基于有限差分方法和粒子法的混合方法(Gerya and Yuen, 2003a, 2007),目前应用广泛.
本文所采用的I2VIS数值模拟是基于单元粒子和有限差分混合的计算方法(Gerya and Yuen, 2003a, 2007).模型参数的敏感性实验通过多因素多水平正交试验设计方法实现,“因素”的多少根据考察参数的个数而定,而“水平”的多少则主要依据实际地质过程中的取值范围而定.在模型实验结果的基础上,为了得出更为直观而精确的定量化结果采用数理方法进行量化分析.
柴达木北缘弧岩浆变质带和超高压变质地体时空上具有良好一致性,因此需要考虑不同圈层的耦合作用.本文分别采用简单模拟和综合模拟的方法,根据有无温度耦合作用和是否存在上涌通道,分别建立三组数值模型: (1) 未考虑温度影响的底辟流模型; (2) 考虑温度耦合的无上涌通道底辟流模型; (3) 考虑温度耦合且具有上涌通道的底辟流模型.通过有限差分法和粒子追踪技术,研究岩石圈、软流圈尺度内地球流体介质在热、重力及构造作用下的流动、变形及应力状态,定量模拟底辟流上涌动力学过程.通过这三个模型我们可以模拟出底辟流上涌过程中速度、温度以及黏度的时空变化过程,并与流体幂次定律速度公式(Weinberg and Podladchikov, 1994)以及Hall和Kincaid(2001)提供的针对海洋俯冲板块流体上涌机理进行对比研究,对柴达木北缘古生代祁连弧的形成过程具有重要的启示意义.
1 数值模拟方法
1.1 控制方程
本文模型采用二维的地球动力学算法“I2VIS”进行数值计算(Gerya and Yuen, 2003a).该算法程序考虑了热-流体动力学的耦合,有三组控制方程:斯托克斯流体动力学方程、不可压缩质量守恒方程、温度演化的能量守恒方程.
(1)斯托克斯流体动力学方程:
(1)
(2)
式中,g表示重力加速度,密度ρ是岩石类型C、部分熔融比例M、压力P及温度T的函数,σ′xx、σ′zz和σ′xz是偏应力张量分量.
(2)不可压缩质量守恒方程:
(3)
其中,vx和vz表示水平速度和垂向速度.
(3)温度演化的能量守恒方程:
(4)
(5)
(6)
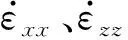
1.2 岩体流变性质
本文采用黏-塑性本构方程表示偏应力和应变率张量,对不可压缩的黏滞性变形则采用下式表示:
(7)
(8)
(9)
式中,ηeff表示有效黏滞系数,将热-流体动力学耦合在一起,可表示为
(10)
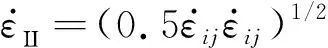
实际岩体的黏-塑性流变结合了韧性与塑/脆性流变.因此,我们在数值计算中采用改进的Drucker-Prager屈服准则(Ranalli, 1995):
σyield=C0+Psin(φeff),
(11)
sin(φeff)=sin(φ)(1-λ),
(12)
(13)
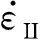
地球动力学算法“I2VIS”(Gerya and Yuen, 2003a),选取ηductile和ηplastic最小者作为实际的黏度参与计算(Ranalli, 1995):
ηcreep=min(ηductile,ηplastic).
(14)
1.3 部分熔融
模型计算中考虑了地壳岩石的部分熔融行为(Gerya and Yuen, 2003b; Burg and Gerya, 2005),根据实验岩石学的约束条件,将温度与岩石部分熔融体积比例之间的关系看做近似的线性关系:
M=0,当T≤Tsolidus,
(15a)
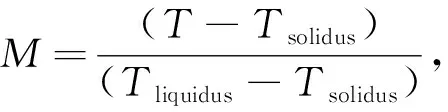
(15b)
M=1,当T≥Tliquidus,
(15c)
式中,Tsolidus和Tliquidus分别表示岩石的湿固相线温度和干液相线温度.部分熔融岩石的有效密度与熔融比例之间的关系如下所示:
ρeff=ρsolid-M(ρsolid-ρmolten),
(16)
式中,ρsolid和ρmolten分别表示固相岩石的密度和熔融岩石的密度,两者均为温度和压力的函数:
ρ=ρ0(1-α(T-T0))(1+β(P-P0)),
(17)
式中,ρ0代表岩石在P0=0.1 MPa压强条件,T0=298 K温度条件下测得的标准密度;α和β分别代表热膨胀系数和可压缩系数.
以上公式表明,地球介质的黏度、密度变化受温度和压力的影响非常大,而随温度、压力变化的黏度、密度对固体地球不同圈层的俯冲、上涌等动力学过程也有直接的影响,因此,以上公式构成了地球动力学热-流体耦合数值模拟的理论基础.
2 柴北缘祁连弧底辟流上涌过程的数值模拟
2.1 未考虑温度影响的底辟流上涌模型
未考虑温度影响的底辟流上涌模型主要研究底辟流的初始半径对底辟流上涌速度的影响,为论述的方便,下文称为模型一.考虑到柴达木北缘超高压变质地体在绿良山、锡铁山、都兰区域南北方向宽15~50 km(Zhang et al., 2005),并且热流体或熔体上涌时伴随着自身物质的扩散和体积不断增大,最终在地壳中的侵蚀范围大于上涌初始半径,本模型设置三组不同半径(5 km, 10 km, 15 km)的底辟流上涌模型进行对比实验.模型一未考虑温度对底辟上涌的影响,黏度和密度均采用为常数.初始模型宽度50 km,深度120 km.几何模型分为三个不同的区域(如图3),不同区域材料赋值不同:1是地壳模块,厚度35 km,黏度1024Pa·s,密度2700 kg·m-3;2是地幔模块,厚度95 km,黏度1020Pa·s,密度3300 kg·m-3;3是初始底辟流,初始黏度1012Pa·s,密度2500 kg·m-3.底辟流初始中心位置位于地表下90 km处开始上涌,模型离散化采用规则的有限差分网格,网格划分为两个部分:第一,网格的划分分辨率50×120,相当于1 km一个格网点;第二,网格内部标记点的划分,这里采用10×10的标记,相当于每100 m一个标记点粒子.模型边界均采用自由滑动边界条件.
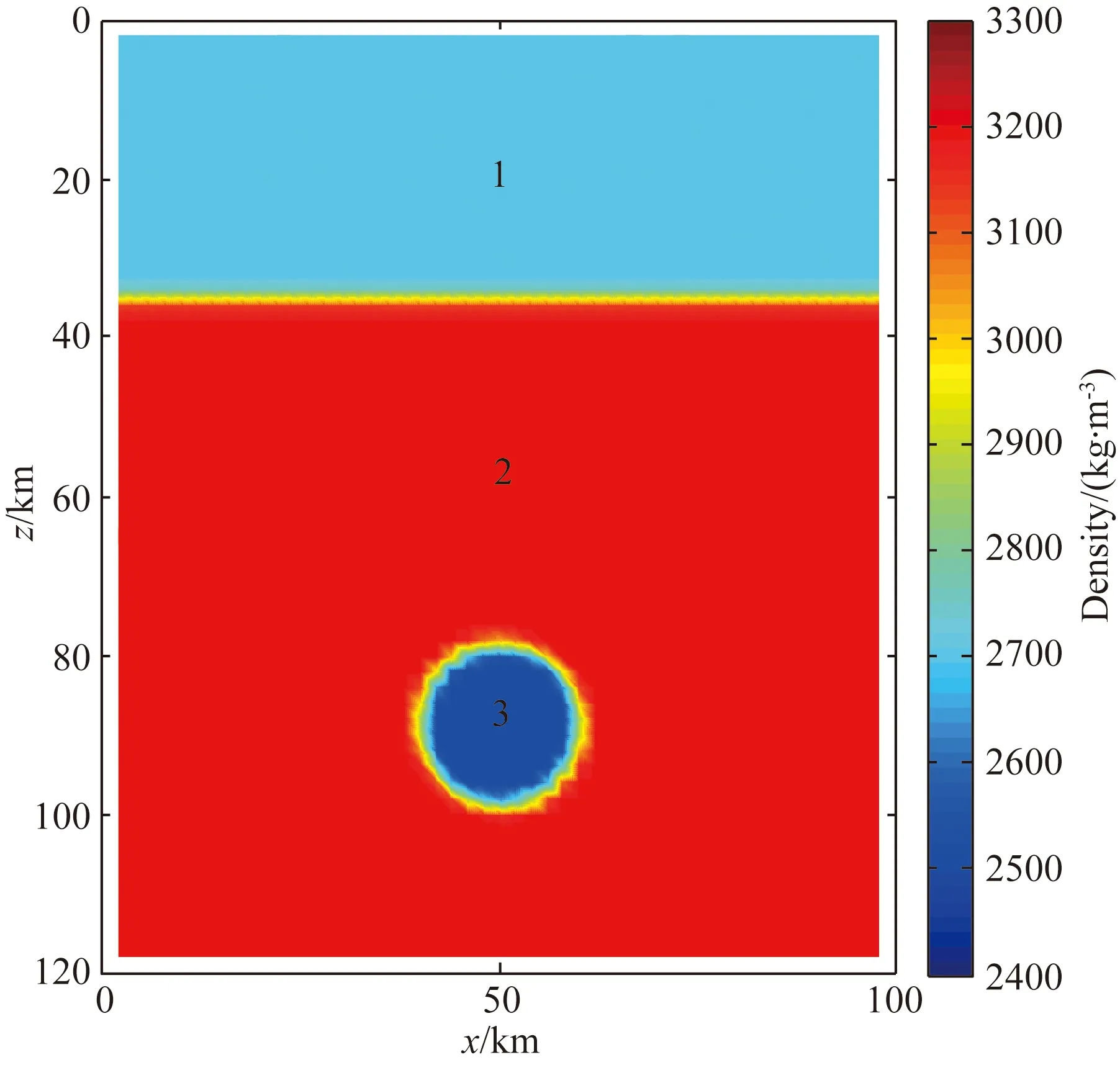
图3 半径为10 km底辟流初始密度示意图上图中,1表示地壳,2表示上地幔,3表示初始底辟流.Fig.3 Schematic diagram of initial density of diapir flow with a radius of 10 kmIn the above figure, 1 denotes the earthcrust, 2 denotes the upper mantle, 3 denotes initial diapir flow.
底辟流上涌过程主要分为四个阶段,这里以半径为10 km的底辟流上涌为例说明(如图4):(1)第一阶段是快速上涌阶段:0~0.01 Ma,底辟流上涌过程中由于密度差形成的正浮力作用值较大,因此在底辟上涌的初期,初始速度值在短时间内从0迅速增大至一个峰值,由于加速过程非常短暂,这段时间相对于模拟研究的时间尺度而言可以忽略不计,这里为了研究方便统一取上涌持续0.01 Ma后的速度为起点进行分析.(2)第二阶段是匀减速上涌阶段:0.01~0.5 Ma,底辟流上涌速度均匀减小,流体和周围地幔进行交代作用,底辟流初始上涌速度为2.1 cm·a-1,上涌速度均匀下降至0.6 cm·a-1以后进入非均匀减速阶段;(3)第三阶段是非均匀减速上涌阶段:0.5~1.8 Ma,底辟流上涌速度随着时间的推移非均匀放缓,在这个时间段内上涌速度逐渐减缓为零,同时由于底辟流属于高塑性流体,流体组分逐渐向水平方向扩散;(4)第四个阶段是稳定阶段:1.8~3.2 Ma,该阶段底辟流上涌速度几乎为零,底辟流双向扩散均达到稳定状态.
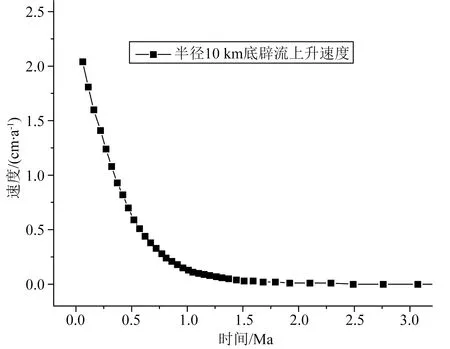
图4 半径为10 km的底辟流上涌速度图(从0.01 Ma作为起点,不包括阶段1)Fig.4 Upwelling velocity of diapir with a radius of 10 km (Starting from 0.01 Ma, excluding stage 1)
以底辟流中心位置为观测点,得出半径为10 km底辟流上涌过程中上涌速度变化的实时曲线,如图4所示.
图5为半径为r=10 km的底辟流半径上升速率模拟示意图.
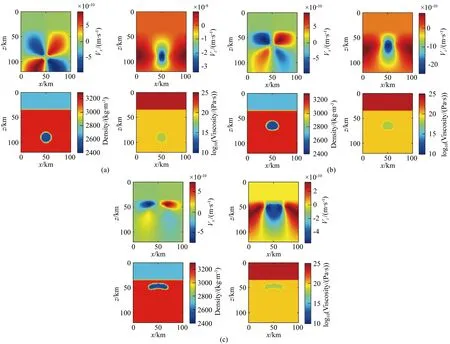
图5 半径为r=10 km的底辟上涌模拟示意图(水平速度Vx,垂直速度Vz,密度及黏度)(a) 0.01 Ma; (b) 0.7 Ma; (c) 1.8 Ma.Fig.5 Simulation diagram of diapir upwelling with radius r=10 km (Horizontal speed Vx, vertical speed Vz, density and viscosity)
半径为5 km, 10 km, 15 km的底辟流上涌速度如图6所示.
通过对比分析三个不同半径(r=5 km,10 km,15 km)的底辟流垂直上涌速度(如图6),我们得到以下实验结论:
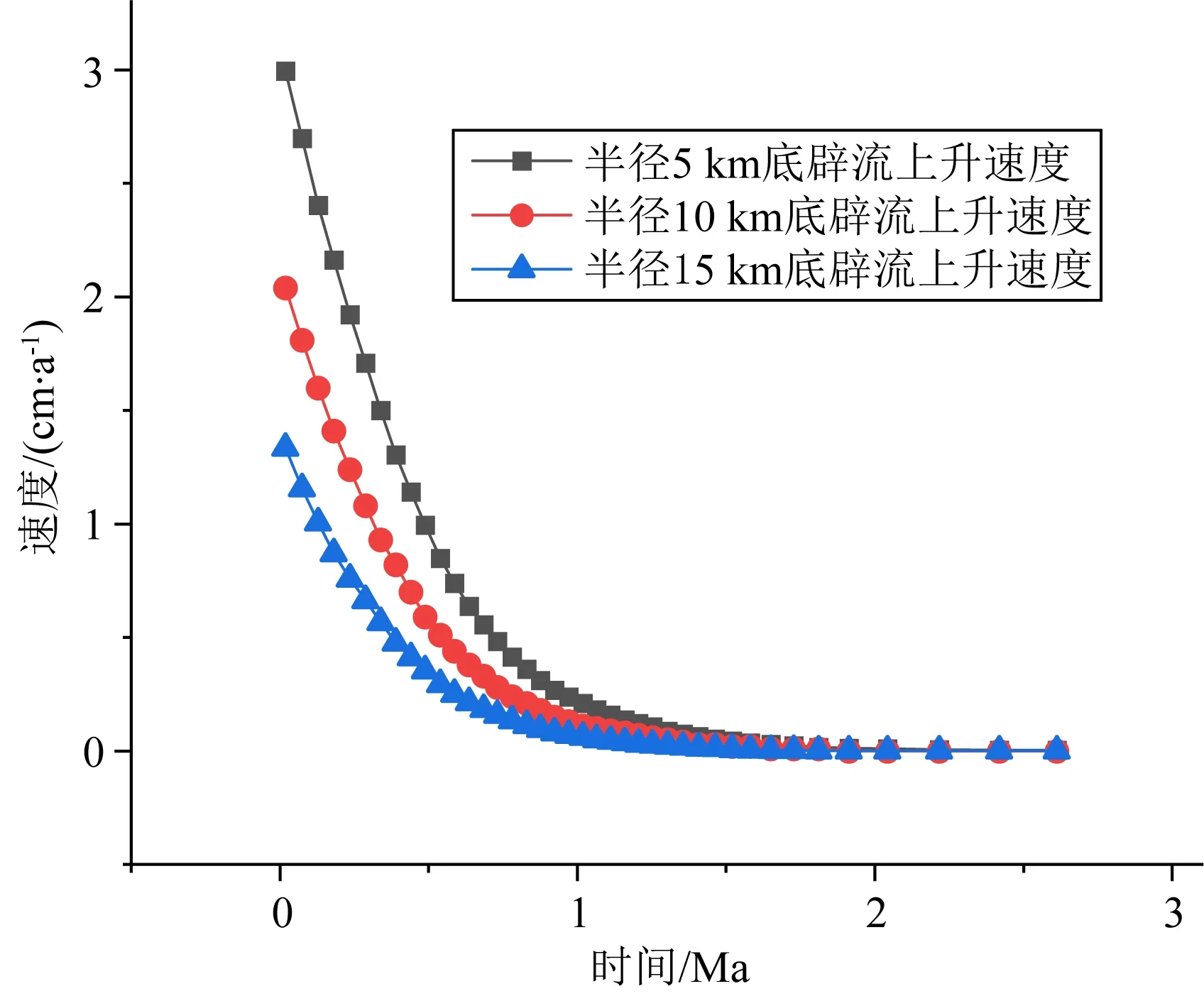
图6 三个不同半径(r=5 km,10 km,15 km)的底辟流上升速度图Fig.6 Ascent speed graph of diapir flow with three different radius (r=5 km,10 km,15 km)
(1)半径大小对底辟流上涌速度的变化具有明显的影响,底辟流半径越大所受到的正浮力作用越大,上涌速度越快,达到稳定阶段的时间也越短,半径为5 km的底辟流在开始上涌2.2 Ma以后速度为零,达到稳定状态;而半径为10 km、15 km的底辟流分别在1.8 Ma、1.5 Ma以后达到稳定状态.
(2)底辟流匀减速上涌阶段,半径越大单位时间内降低的速度值越少,半径5 km的底辟流每百万年下降速率为4.3 cm·a-1,而半径10 km、15 km的底辟流每百万年下降速率分别为2.6 cm·a-1、1.9 cm·a-1.
(3)在不考虑熔融和温度的影响下,底辟流上涌过程非常迅速,半径大小对上涌速度的影响至关重要,三个不同半径(5 km、10 km、15 km)的底辟流从开始上涌至速度为零的稳定时间均不超过3 Ma.
综上所述,通过实验模拟三组不同半径的底辟流上涌过程得到相关的实验结果为:半径5 km、10 km、15 km的底辟流平均上涌速度分别为2.7 cm·a-1、3.3 cm·a-1、4.0 cm·a-1.由上图可知,在同等地质条件下,随着半径的增大底辟流上升至下地壳的速度越快,所消耗的时间越短.三个不同半径的底辟上涌稳定时间都不超过3 Ma,这和目前的观测成果底辟流从90 km深的地幔深度运移至地壳30 km处耗时小于10 Ma在时间上具有较好的一致性(Yin et al., 2012).
2.2 考虑温度耦合的无上涌通道底辟流上涌模型
在热的底辟流上涌过程中,不可避免地伴随着与周围地幔的热交换作用,自身温度黏度和密度都会实时发生变化.而模型一未考虑温度变化的影响,黏度、密度均为常数.为了更加真实的模拟现实的底辟流上涌过程,我们考虑岩石的熔融效应,在流体速度场的基础上耦合温度场,建立温度耦合的无上涌通道底辟流上涌模型,为论述的方便,将之称为模型二.与模型一进行对比分析,研究温度变化对底辟流上涌过程的影响.同时为了对比分析多个底辟流上涌的影响,将模型二分为单底辟流上涌模型和双底辟流上涌模型.
如前文所述,底辟流上涌过程中温度的变化会导致自身黏度以及密度随时间变化.模型二中,我们假设岩浆来自岩石圈下面的岩浆源区(SMSR)(Gerya and Burg, 2007),初始的熔融体为20%的熔体分数,随着底辟流的上涌,熔融的岩浆温度逐渐下降,熔体分数也随之改变,岩浆上涌至地表时与岩石圈发生熔融反应并逐渐冷却.模型二的主要参数见表1.

表1 主要模型参数(参考Ranalli, 1995)Table 1 Main model parameters (Refer to Ranalli, 1995)
模型二宽度100 km,深度120 km,底辟流初始中心位于地表下90 km处(图7),模型顶部设置5 km沉积层,沉积层下地壳厚度为35 km,其中上地壳20 km,下地壳15 km.上地壳、下地壳和底辟流分别近似采用石英岩,斜长石和基性熔融体的流变参数,见表1.关于热边界条件,模型顶部保持温度0 ℃,大陆岩石圈底部边界温度1300 ℃(Turcotte and Schubert, 2002),软流圈地幔的温度梯度为 0.5 ℃/km,两侧边界的水平方向温度梯度为零(即零热流).模型底部采用的是外部边界固定温度条件(Li et al., 2010),即在模型底部120 km处的渗透边界上,温度和热流均可以随着模型计算而动态调整.模型二所采用的不同岩层初始黏度和密度值参考模型一,模型离散化采用规则的有限差分网格,网格划分为两个部分:第一,格网点的划分分辨率100×120,相当于1 km一个格网点;第二,网格内部标记点的划分,这里采用10×10的标记,相当于每100 m一个标记点粒子.模型顶部设置黏滞层,地壳表面之上,与自由滑动的模型顶界面之间,设计一层相对高黏滞度的伪空气层,其与上地壳的接触面用以模拟地形起伏面,该地形起伏面包含了近似的剥蚀和沉积作用(如Li and Gerya, 2009).模型中除了底部边界,其他边界均采用自由滑动速度边界条件.
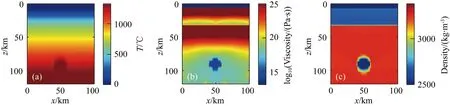
图7 单个底辟流上涌示意图(a) 初始温度示意图; (b) 初始黏度示意图; (c) 初始密度示意图.Fig.7 Schematic diagram of a single diapir flow upwelling(a) Initial temperature; (b) Initial viscosity; (c) Initial density.
单个底辟流上涌实验结果表明,底辟流上涌过程中由于自身温度较高和周围地幔的温差大,上涌初期进行剧烈热交换,随着上涌时间的延续温度迅速减小,并且伴随着自身物质扩散和体积不断增大,最终形成以底辟流中心为分界点的双拱形地幔对流,在上涌2.5 Ma以后,在地表下75 km左右停止上涌(图8).这是由于底辟流在上涌过程中,不仅仅是流体本身的运动,还存在由于温度差异而引起的密度、黏度等物理参数的实时变化.伴随着上涌过程中不断地与周围环境进行热交换导致自身热量的流失,底辟流的黏度和密度随之增大,导致底辟流上涌至地表下75 km左右时温度和黏度与周围地幔相近,正浮力为零,因此相比常黏度模型相同半径的底辟流上涌时不能完全抵达壳幔交界处.温度场是底辟流上涌过程重要影响因素.单个底辟流无法上涌至壳幔边界处,难以穿越地幔楔直接出露地表.
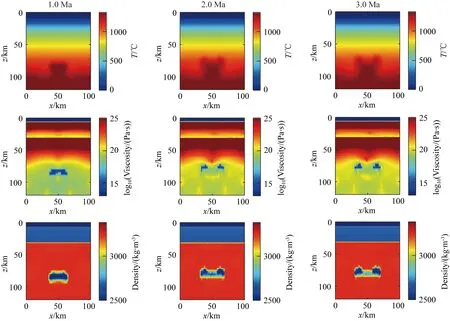
图8 半径为10 km的单个底辟上涌模型图 (1.0,2.0,3.0 Ma三个不同时刻温度、密度和黏度的分布)Fig.8 Single dip upwelling model with a radius of 10 km (The distribution of temperature, density and viscosity at three different moments of 1.0, 2.0, 3.0 Ma)
根据柴达木北缘祁连弧地区地表超高压变质岩的分布情况可知底辟流上涌过程并非是单个上涌.伴随着海洋板块的俯冲作用,底辟流上涌实际上是一个持续增量的过程,为了进一步探究底辟流上涌的情形,我们设计双底辟流上涌模型(如图9所示),分别在地表下90 km,70 km设置半径10 km的底辟流,模型参数与单个底辟流一致,模型运行结果如图10所示.
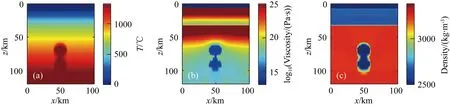
图9 双底辟流上涌示意图(a) 初始温度示意图; (b) 初始黏度示意图; (c) 初始密度示意图.Fig.9 Schematic diagram of double diapir flow upwelling(a) Initial temperature; (b) Initial viscosity; (c) Initial density.
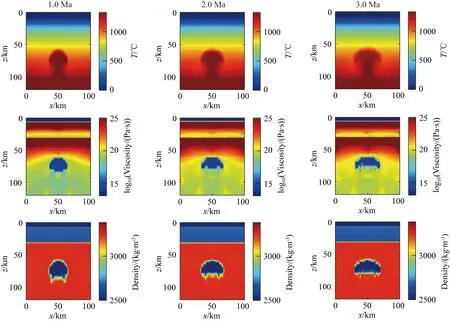
图10 半径为10 km的双底辟上涌模型图 (1.0,2.0,3.0 Ma三个不同时刻温度、密度和黏度的分布)Fig.10 Double diapir upwelling model with a radius of 10 km (The distribution of temperature, density and viscosity at three different moments of 1.0, 2.0, 3.0 Ma)
双底辟流上涌实验结果表明,底辟流上涌过程中伴随着与周围岩体剧烈的热交换和自身物质扩散,从最初上涌时的两个半径为10 km的球形迅速合成一股较大的底辟流,同时以新形成的大的底辟流中心为分界点双向侵蚀,在上涌至3 Ma以后,持续上涌至地表下60 km左右(图10),而单个底辟流则上涌至2.5 Ma时则停止上涌.在相同的时间内(3 Ma),双底辟流上涌比单底辟流在垂直方向侵蚀的距离更长,并且水平方向也没有发生弥散现象.因此,我们认为当底辟流上涌的量足够大时,会在原来底辟流上涌的位置上方形成稳定的岩浆通道,在此基础上,底辟流会在正浮力的推动下沿着岩浆通道上涌,不断地侵蚀壳幔边界,在短时间内(小于1 Ma)上涌融体不断地侵蚀减薄上覆地壳,最终出露地表形成岩浆弧.当岩浆通道足够宽时,随着俯冲的进行,在熔融过程中密度和黏度相对较小的变质岩沿着岩浆通道快速上涌至地表,形成地表可观测到的超高压变质岩石.
由于岩浆通道形成后的上涌时间很短,北柴达木超高压变质带和岩浆弧的形成在时间和空间上一致.
2.3 考虑温度耦合和上涌通道的底辟流上涌模型
为了进一步说明柴达木北缘祁连弧的形成机理,针对海洋俯冲底辟流模式中存在稳定岩浆上涌通道(Yin et al., 2012),我们建立温度耦合和上涌通道的底辟流上涌模型,为论述的方便,下文称为模型三(如图11).模型三设置了宽为5 km的软弱层模拟岩浆上涌通道.模型三所采用的不同岩层初始黏度和密度值参考模型一,模型离散化采用规则的有限差分网格,模型尺寸为100 km×120 km,网格分辨率为100×120,相当于1 km一个网格;第二,网格内部标记点的划分,这里采用10×10的标记,相当于每100 m一个标记点粒子.地层结构、热边界条件参考模型二.上地壳、下地壳和底辟流采用的流变参数见表1.模型顶部设置黏滞层,即地壳表面之上,与自由滑动的模型顶界面之间,设计一层相对高黏滞度的伪空气层,其与上地壳的接触面用以模拟地形起伏面,该地形起伏面包含了近似的剥蚀和沉积作用(Li and Gerya, 2009).模型中除了底部边界,其他边界均采用自由滑动速度边界条件.
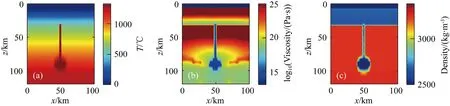
图11 模型三示意图(a) 初始温度示意图; (b) 初始黏度示意图; (c) 初始密度示意图.Fig.11 Schematic diagram of model 3(a) Initial temperature; (b) Initial viscosity; (c) Initial density.
图11给出了模型三0.01, 0.05, 0.1 Ma三个不同时刻温度、密度和黏度的分布.模型三的结果表明,模型运行初期0.01 Ma内,底辟流快速上涌冷却,同时伴随着周围岩体快速热传导增温,尤其以初始位置正上方的上地壳岩体升温最为强烈.0.01~0.05 Ma内,下地壳内基性岩浆在巨大正浮力作用下缓慢而稳定地上涌侵入上地壳底部并水平向外扩展.0.05 Ma后,底侵岩浆初具规模,下地壳基性岩浆开始快速侵入,此后经过约0.05 Ma,几乎所有的岩浆侵入到上地壳底部,平铺于下地壳界面之内.在快速上升熔体的冲击及熔体和软流圈物质对岩石圈地幔底部热侵蚀的共同作用下,对上覆岩石圈地幔底部造成一定程度的破坏.然后持续增多的板片熔体对上覆岩石圈地幔的破坏逐渐向岩石圈浅部蔓延,加深减薄程度;同时在熔体上升过程中诱发的地幔对流作用下,上覆岩石圈地幔的破坏也逐渐向陆内方向扩展,扩展减薄范围,从而导致对上覆大陆在垂向和水平向的双重破坏,如图10所示,半径为10 km的底辟流上涌过程中,垂向地壳减薄约15 km,水平向陆内侵蚀延伸约30 km,随着底辟流持续增量上涌,在地壳内部形成蘑菇状侵入体.即具有稳定岩浆通道的底辟流上涌过程中,从地幔深处90 km上涌至壳幔边界时在水平方向的侵蚀范围要比垂向的侵蚀范围大一倍左右.
另外,模型黏度场和温度场结果显示,底辟流上涌诱发的向上流场强烈侵蚀作用导致上覆岩层温度升高300~500 ℃,黏度降低为初始时刻的1/100~1/1000.随着底辟流上涌在岩石圈地幔向浅部和向陆的双重破坏,具有更低黏度,更高热流的软流圈物质也会沿着已经形成的岩浆通道上涌,同时双向蔓延导致地幔相对较浅部位被弱化,产生剧烈熔融作用,使得上涌熔体在莫霍面附近的大陆岩石圈地幔底部逐渐冷却并稳定下来.实际情况不仅仅是单个底辟流上涌,而是伴随含水量较高的海洋板块俯冲,在地幔深处高温高压条件下板块迅速发生脱水熔融,上涌熔体的体积不断增大,底辟流体入侵地壳双向侵蚀的范围也随之不断扩大,最终出露地表形成岩浆弧,该过程对古生代柴达木北缘地区热地幔物质的熔融溢出形成祁连岩浆弧提供理论参考意义.
3 讨论
3.1 三个模型对比分析及意义
底辟流上涌实质上对应地幔对流过程中的上升流,不仅为地球板块运动和洋脊扩张提供了重要的动力来源,同时为地球内部各圈层物质迁移提供了重要输出.本文实验模型具有一定的普适性,讨论了底辟流上涌的一般性问题,研究成果可以为古生代柴达木北缘地区热地幔物质的熔融溢出形成祁连岩浆弧的过程提供理论参考意义.三个模型的实验结论及优缺点如下:
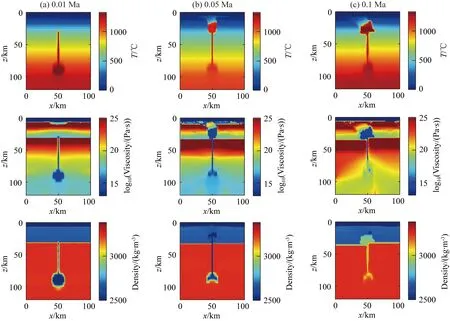
图12 不同时刻半径为10 km的底辟流上涌模型图(a) 0.01 Ma; (b) 0.05 Ma; (c) 0.1 Ma.Fig.12 The upwelling model of the diapir with a radius of 10 km at different time
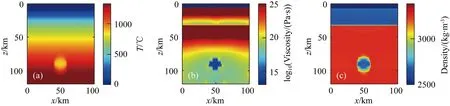
图13 柴北缘都兰南部区域单个底辟流上涌初始模型(a) 初始温度示意图; (b) 初始黏度示意图; (c) 初始密度示意图.Fig.13 Initial model of upwelling of a single diapir in South-Dulan region of North Qaidam(a) Initial temperature; (b) Initial viscosity; (c) Iinitial density.
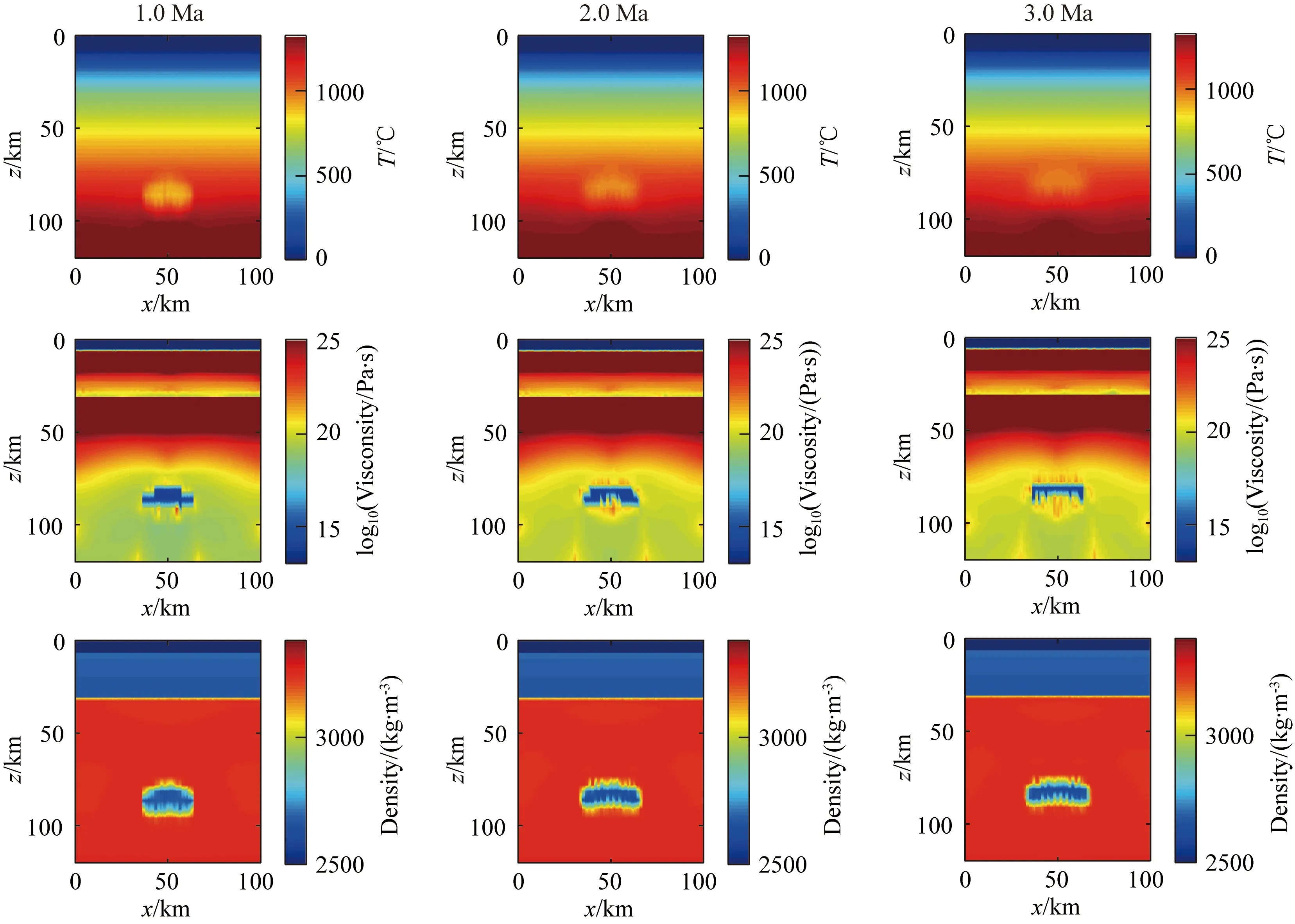
图14 不同时刻柴北缘都兰南部区域单个底辟流上涌模型图(a) 1.0 Ma; (b) 2.0 Ma; (c) 3.0 Ma.Fig.14 Diapir flow upwelling model diagram in South-Dulan region of North Qaidam at different times
模型一主要是从运动学的角度分析了底辟流上涌的速度变化,缺点是没有考虑温度场对上涌过程中底辟流的密度和黏度变化,结果表明在不考虑温度场的情况下,底辟流上涌过程中形状基本不变,单个底辟流上涌可以到达下地壳,但无法到达地表;为了更加真实地模拟底辟流上涌过程,模型二在模型一的基础上增加了温度场,模型结果表明单个底辟流无法上涌至地表,并且底辟流上涌过程中的形状不能保持为原来的球形,而是逐渐扩散,未到达下地壳便弥散和消亡在地幔中;而两个底辟流上涌时,底辟流双向侵蚀距离明显加大,并且在相同的运行时间内(3 Ma)底辟流保持球形形状,并未发生弥散现象,而且侵蚀作用也并未停止.由此我们推出,持续增量上涌的底辟流必然会形成直达地表的稳定岩浆通道,岩浆通道的形成导致不断补充的底辟流在水平和垂直两个方向持续侵蚀周围岩体,最终形成出露地表的岩浆弧.模型三在模型二的基础上模拟了形成稳定岩浆通道后底辟流上涌的情形,结果表明,底辟流上涌时间大大缩短,侵蚀效率也明显加快,底辟流在0.1 Ma 左右即从地表下90 km 上涌至地表,最终形成出露地表的岩浆弧.正是由于岩浆通道形成后极大的缩短了上涌时间,导致北柴达木超高压变质带和岩浆弧在形成时间和空间上一致.
综上所述,模型一没有考虑温度的影响,只考虑底辟流半径对底辟流上涌速度的影响;模型二考虑了温度耦合的影响,但没有考虑上涌通道的影响,实际上是海洋板块俯冲时,底辟流上涌初期阶段过程,其最终结果是形成上涌通道;模型三是考虑温度耦合和上涌通道的底辟流上涌模型,伴随着持续增量的底辟流上涌,在底辟流上方形成稳定的岩浆通道时的过程,模拟的是底辟流最后阶段快速上涌的过程.
3.2 柴北缘都兰南部区域底辟流上涌模拟
根据柴北缘都兰南部区域超高压变质岩石上涌现代观测数据(Song et al., 2003),采用和观测值一致的底辟流初始上涌温度,并且为了进一步解释说明多个底辟流上涌对实验结果的影响,设计双底辟流上涌对照组模型(如图15、16),初始半径均设置为10 km.底辟流上涌的初始温度略低于周围岩体的温度,上涌时伴随着剧烈热交换,自身温度会先升高,由于底辟流本身的黏度和密度值比周围岩体小,温度升高导致熔融比例加大,其黏度和密度会进一步减小,由此导致侵蚀现象的发生.模型结果显示,在相同的时间内(3 Ma),双底辟流上涌时,底辟流向上侵蚀运移的距离大于单个底辟流上涌距离,进一步说明了当持续增量的底辟流上涌时,底辟流向上侵蚀运移的距离会不断加大,最终形成稳定的岩浆通道,从而形成出露地表的岩浆弧.
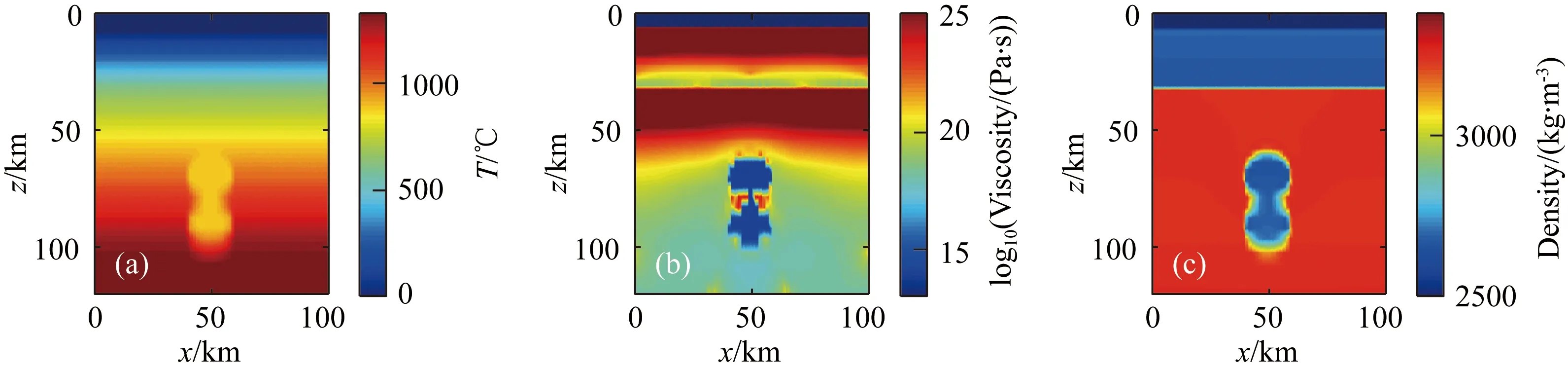
图15 柴北缘都兰南部区域双底辟流上涌初始模型(a) 初始温度示意图; (b) 初始黏度示意图; (c) 初始密度示意图.Fig.15 Initial model of upwelling of double diapirs in South-Dulan region of North Qaidam(a) Initial temperature; (b) Initial viscosity; (c) Initial density.
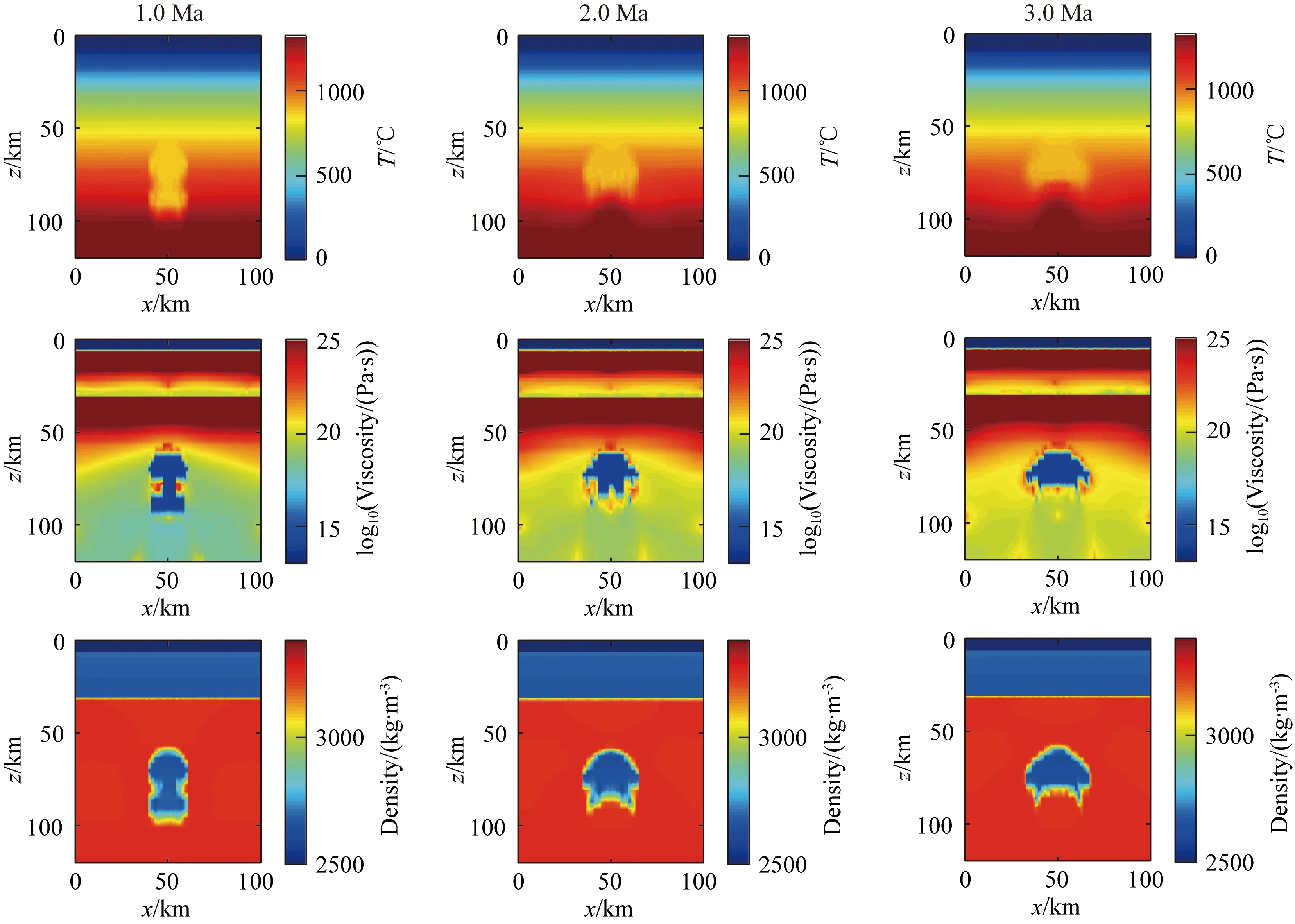
图16 不同时刻柴北缘都兰南部区域双底辟流上涌模型图(a) 1.0 Ma; (b) 2.0 Ma; (c) 3.0 Ma.Fig.16 Diagram of the upwelling model of double diapir flow in South-Dulan region of North Qaidam at different times
3.3 与前人研究结果对比
模型一主要研究了单个底辟流上涌时单一变量半径对上涌速度的影响,实验结果表明半径越大,上涌速度越快.但实际情况是在海洋板块俯冲时由于自身脱水熔融作用在地幔深度约90 km左右会导致大量的底辟上涌,这些底辟有可能是单个、多个,或者持续增量的形式同时上涌,而多个底辟上涌过程中由于大的底辟上涌速度快,在上涌过程中可能会追上半径小的底辟,两者产生黏结作用后,以两者黏结前的速度中间值向地壳运移.
针对单一底辟流的上涌速率,我们根据Hadamard Rybczynski方程计算牛顿流球体穿过幂次定律流进行比较分析底辟流上涌时的速度(Weinberg and Podladchikov, 1994).
(18)
其中μeff是周围环境流体的有效黏度,这里我们采用的常黏度进行计算,取值1020 Pa·s,A是材料常数,μsph是球体的牛顿黏度,我们这里为了简化模型采用的也是常黏度,取1018Pa·s,r是流体半径,Δρ是流体与周围地幔密度差,参数n是常数2(Miller et al.1988),参数Xsol,M和G是m=1/n的函数.
Xsol=1.3(1-m2)+m,
M=0.76+0.24m,
G=2.39-5.51m+3.77m2.
(19)
Xsol用于纠正流体的速度,Xsol,M,G都是和材料相关的参数,三个参数配合起来用于对流体下降速度的纠正.代入公式计算可得到Xsol=1.48,M=0.88,G=0.76.根据Hadamard Rybczynski公式计算出来的底辟流上升速度理论值为V=6.67 cm·a-1.通过实验模拟三组不同半径的底辟流上涌模型得到相关的实验结果为:半径为5 km的底辟流平均上涌速度2.73 cm·a-1, 半径为10 km的平均上涌速度3.33 cm·a-1, 半径为15 km的平均上涌速度4 cm·a-1.实验结果和理论值在数量级上一致,由于考虑到地幔对流的影响,三组不同半径的底辟流上涌模型模拟值略低于理论值.
另外,针对Hall和Kincaid(2001)提出的底辟流通过地幔楔的机理,我们的实验结果也进行了相关对比分析.Hall和Kincaid(2001)提出的流体上涌方式和一个无量纲的常数Bn值有关,Bn值的计算方法如下:
(20)
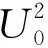
Hall和Kincaid(2001)提供了一个针对海洋俯冲板块流体上涌的概念框架,并且通过模型实验得出不同的Bn值范围对应不同上涌模式,但由于实验过程中采用的是等黏度,等温度模型,忽略了模型上涌过程中温度对流体黏度以及熔融的影响,与现实条件下底辟流上涌过程黏度随温度实时变化不符.另外,Hall和Kincaid(2001)模型中底辟流上涌速度假定是均匀的,存在以上两点假设,而我们的模型设计做了相应的改进,不仅考虑温度场对于底辟上涌过程密度和黏度的变化,上涌速度也是受到黏度和密度改变产生实时的变化.同时考虑了底辟流上涌过程中各个阶段,各圈层之间巨大的黏滞度差异、复杂的岩体黏-弹-塑性本构关系(Hall et al., 2003).
将本文模型二的实验参数带入公式(20)计算所得的Bn值属于高阈值范围.根据模型二实验结果,单一底辟流无法以固定的直径上涌,而是在上涌过程中半径不断增大,并伴随物质扩散直至消亡在地幔中.所以Hall和Kincaid(2001)提出的针对上述不同的Bn值范围,底辟流对应不同上涌模式的结论还应结合实际温度场影响条件下,进一步的完善与讨论.
板块俯冲导致的大量底辟流上涌,岩浆的持续上涌并由此形成的岩浆通道是导致地壳增厚熔融的重要因素(吴福元等,2014).在底辟流上涌的初始阶段,单个底辟流上涌最终不能上涌至下地壳说明单个板片熔体不足以透过地幔岩石层向浅部侵蚀蔓延.因此,我们认为实际情况可能是由于随着祁连海洋板块不断俯冲至地幔深处,自身脱水熔融产生持续增量的底辟不断上涌导致的脱水熔融作用会使地幔楔岩体的熔点降低,并且伴随着巨量熔体向上迁移进而产生大量幔源岩浆;另一方面,板片富水流体或含水熔体的加入导致熔融流体在向上迁移的过程中极大降低地幔楔内岩石的流变强度和黏滞度,并强烈扰动地幔对流场,进而导致对岩石圈地幔的热侵蚀作用以及多种构造变形的发生.在地幔对流的共同作用下沿着岩石层的软弱带和断层裂隙不断向大陆方向融熔侵蚀,最终形成直达地表浅层的岩浆通道,即安第斯模型中的底辟流模型是最终导致祁连弧形成的重要机理(Yin et al., 2012).岩浆通道形成以后,随着海洋板块的俯冲,冷的变质岩会沿着岩浆通道快速上涌出露地表,形成超高压变质带.
3.4 现代观测数据
根据绿梁山橄榄岩测定的SHRIMP锆石U-Pb年龄数据,超高压变质岩产生在488~495 Ma(Zhang et al., 2005),同样的研究表明,锡铁山超高压变质岩产生在478~488 Ma(Zhang et al., 2005),都兰区域产生在422~450 Ma(Song et al., 2005; Mattinson et al., 2006),上述数据表明柴达木北部超高压变质作用可能持续了数十百万年.稀土元素研究表明,绿梁山地区的石榴石橄榄岩来源于海洋地幔,这些岩石经历了早古生代的变质作用(457±22 Ma)(Song et al., 2006).通过检测榴辉岩的原岩和地质年代,Zhang等(2005) 认为绿梁山和锡铁山具有截然相反的减压路径:前者减压时间非常短,后者则在下地壳中停留了相对较长的时间(>80 Ma).减压时间短可能是由于绿梁山地区相比锡铁山地区地壳岩石层软弱带更集中,或者该区域岩浆上涌量巨大,侵蚀作用非常剧烈,从流体上涌至形成的岩浆通道经历的时间较短,那么对应的岩浆通道形成后变质岩石减压出露地表的时间会相对短.
白云母的40Ar/39Ar热力学分析表明绿梁山超高压变质岩从465~390 Ma运移了<10 km的距离,即超高压变质岩在中地壳停留了超过70 Ma.我们的模拟结果表明,对于已经形成岩浆通道的单个底辟或者超高压变质岩而言,向上减压运移的时间就是整个流体上涌过程经历的时间,该过程只需要数个百万年就可以完成,而超高压变质岩在中地壳中停留时间漫长则是由于中地壳至上地壳的上涌通道并未形成.因此,岩浆上涌通道的形成无论是对于超高压变质岩出露地表所经历的减压时间还是对于地表岩浆弧的形成时间均具有重要的影响.上涌通道形成时间越早,岩浆弧出露地表的年代越久远,同样对应的超高压变质岩石减压时间越短.而从底辟流熔体开始上涌至上涌通道的形成时间则与俯冲区域上覆岩层的软弱带以及上涌流体的体积量有关,软弱带越集中,形成时间越短;上涌流体的体积越大,即半径越大,上涌速度越快,流体地幔对流越剧烈,则垂向侵蚀的速度会越快对应岩浆通道的形成时间越短.
柴达木北缘超高压变质岩地体榴辉岩的原岩可能来源于两个途径:一种是沿着大陆裂隙运移至地表的镁铁质高温岩墙形成的火成岩,另一种是在岛弧或洋中脊扩张中心产生的大洋板块碎片.绿梁山和锡铁山榴辉岩Nd同位素数据表明,其超高压变质岩石来源于高度亏损地幔,现代观测表明榴辉岩来源于弧后和大洋中脊,而非来源于大陆(Zindler and Hart, 1986).柴北缘都兰区域的稀土元素研究表明榴辉岩的原岩为洋中脊玄武岩或海山玄武岩(Song et al., 2003).以上元素测定结果支持柴达木北缘祁连弧底辟流上涌模式为具有稳定岩浆通道的底辟流模型(Yin et al., 2012).因此,安第斯型底辟流模型可以较好地解释早古生代青藏高原柴北缘祁连弧的形成过程.
4 结论
本文针对前人对超高压变质岩形成机制的不同地质解释,从简单模拟到综合模拟,建立三组数值模型,考虑了底辟流的半径、温度耦合、上涌通道等因素对超高压变质岩的形成过程进行了系列数值模拟实验,研究结果对早古生代柴北缘祁连弧的形成过程有一定的启发意义.取得了几点认识:
(1)单个底辟流很难直接上涌至下地壳,早古生代柴北缘超高压变质地体和岩浆弧可能是由于多个底辟流持续上涌,最终发育稳定岩浆通道形成的.岩浆通道的形成对于超高压变质岩石的减压时间以及岩浆弧的形成时间均具有重要影响.
(2)单个底辟很难直接上涌至下地壳,柴达木北缘超高压变质地体和岩浆弧可能是由于多个底辟流持续上涌,最终发育稳定岩浆通道形成的,并且岩浆通道的形成对于超高压变质岩石的减压时间以及岩浆弧的形成时间均具有重要影响.
(3)具有稳定岩浆通道的单个底辟流从地幔深处90 km上涌至壳幔边界的过程中,在水平方向的侵蚀范围要比垂向侵蚀范围大一倍左右.
(4)安第斯型底辟流模型可以较好地解释早古生代青藏高原柴北缘祁连弧的形成过程.
致谢感谢审稿专家对本文提出宝贵修改意见,同时感谢皇甫鹏鹏、王少坡、徐佳静对本文的建议和帮助.
