RMFS订单拣选系统动态货位再指派研究
2021-05-07徐翔斌马中强
徐翔斌,马中强
(华东交通大学 交通运输与物流学院,江西 南昌 330013)
0 引言
基于移动机器人的拣货系统(Robotic Mobile Fulfillment System, RMFS)是一种全新的货到人订单拣选系统,相比于人工和AS/RS(automated storage and retrieval system)拣货系统(统称传统拣货系统),在拣货效率和准确性以及仓库空间利用率等方面存在诸多优势,特别适合需求波动性大、时效性强的电商、超市以及工厂等企业的订单拣选,已在亚马逊、京东以及菜鸟等公司得到成功应用[1]。
货位指派作为RMFS的一个重要优化方向,指的是将库存存货单元(Stock Keeping Unit, SKU)或货架分配到仓库中的合适货位/储位,使订单拣选的时间/距离最短,科学的货位指派方法可缩短行走距离、降低搜寻时间以提高仓库拣货效率[2]。Hausman等[3]最早对传统拣货系统的货位指派策略进行研究,随后的文献分别从需求相关性[4-5]、出货量[6]、存储空间指数(Cube-per-Order Index, COI)[7]、周转率[8]以及需求和结构相关性[9]等方面进行了更加深入的研究。
与传统拣货系统不同,RMFS的货位指派问题可分为货架储位指派(货架储位的一次性指派和再指派问题)和SKU上架指派(考虑SKU关联性的上架指派问题)两种。Xiang等[10]对RMFS的SKU上架指派和订单分批问题进行了协同优化,在考虑SKU关联性的前提下以货架每层只存储一种SKU的方式进行上架指派;Yuan等[11]分别考虑了随机、基于类和基于周转率的指派策略,进一步对货架储位指派进行了研究,研究表明基于类的指派策略效果更好,并且发现将SKU分为3类时的优化效果最为显著;随后Roy等[12]和Weidinger等[13]分别从随机指派和分散指派两方面对RMFS的货架储位指派和SKU上架指派进行了研究;在此基础上,Weidinger等[14]进一步将货架储位再指派(Pod Location Reassignment, PLR)问题看作特殊区间调度问题进行研究,设计了自适应算法,结果表明其提出的PLR适应性指派规则比传统的指派策略要好,但未考虑动态情况下的货位再指派问题。在实际情况中,客户对订单的配送时限和成本要求越来越高,由于受促销、季节以及产品周转率和生命周期等因素的影响,需要对RMFS的仓库布局不断优化调整来适应这种变化,从而达到满足客户需求的目的。因此,在RMFS中,考虑动态情况的PLR问题要比传统的一次性货位指派更具现实意义[15]。
鉴于此,本文以具有较大需求波动性和较强需求时效性的电商、超市和工厂的RMFS仓库为研究背景,对动态货架储位再指派(Dynamic Pod Location Reassignment, DPLR)问题进行研究,将其看作多阶段的动态决策问题,考虑仓库布局的动态连续变化关系。首先,构建了反映仓库布局实时变化的混合整数规划模型;然后,设计了考虑动态关系的启发式算法用于求解大规模的DPLR问题;最后,通过数值分析验证了模型和算法的有效性,并通过与传统指派策略对比说明了本文提出的模型和算法可以实现仓库布局的最佳优化。
1 问题描述及模型构建
1.1 问题描述
DPLR是指移动货架在工作站台完成拣货任务后,在被机器人重新送回存储区时,为其重新指派合适储位的过程。DPLR本质上是为货架重新指派合适的储位,使其在仓库内的存储位置与SKU的需求模式相匹配,即畅销SKU所在的货架存储在靠近拣货站台的区域(如图1A区),滞销SKU所在的货架存储在远离拣货站台的区域(如图1C区)。本文考虑基于开放储位仓库布局的DPLR问题,开放储位是指仓库储位除存储移动式货架外,还预留小部分空闲储位的情况,适当的开放储位有助于仓库布局的调整,可缩短拣货的时间/距离[1]。DPLR的具体过程如图1所示,首先将仓库存储区域按距拣货站台的距离分为A、B、C三个区域,分别用于存储畅销、一般和滞销SKU。图1中的畅销SKU所在货架l(黑底网格线标识)当前位于滞销SKU存储区C,在拣货周期t,货架l被机器人搬出至拣货站台,拣货人员完成SKU拣取后,再由机器人送回存储区存储。由于该货架中SKU的需求模式与其存储区域不匹配,DPLR需对该货架进行重新指派,因此该货架在被送回存储区域时,将被指派到黄金储位区A的开放储位1中;同样,滞销SKU所在货架l′也将被重新指派到存储区C的开放储位2中。上述过程随着拣货过程实时动态进行,最终使得整个仓库的存储结构与SKU的需求模式相匹配。

1.2 参数及变量定义
DPLR模型参数及变量分别定义如表1和表2所示。

表1 基本参数

表2 决策变量
1.3 指派策略设计
DPLR的目的是使货架在仓库中的存储位置与其需求模式(存储的SKU)动态匹配,货架的需求模式可用货架周转率fl描述,货架周转率计算存在两种情况:当货架只存储一种SKU时,fl为该SKU的需求频率;当货架存储多种SKU时,fl为其存储所有SKU需求频率的均值;货架的存储位置可用其所在储位i距拣货站台的距离di来衡量。在此基础上,本文提出基于货架与储位匹配度的动态储位指派策略,设计货架需求频率与储位距离关联性指标Cli来指导DPLR进行动态储位优化,Cli为货架周转率与储位至拣货站台距离之比,Cli=fl/di。Cli是将需求频率高/低的货架分别指派到距拣货站台较近/远的储位,从而实现SKU的存储位置与需求模式匹配。
1.4 模型构建
模型假设:①每个货架存储一种SKU,并且每种SKU只存储于一个货架;②不考虑缺货和补货情况;③订单信息已知;④不考虑机器人充电、道路拥堵等情况。在此基础上,构建DPLR的混合整数规划模型如下:
(1)
s.t.
(2)
(3)
(4)
(5)
(6)
(7)
∀i∈I′,l∈L′,t∈T′;
(8)
(9)
(10)
目标函数(1)表示货架与储位匹配程度最大。式(2)~式(10)为约束条件,其中:式(2)表示任意货架在任意时刻必须存储到一个储位;式(3)表示任意储位在任意时刻有货架存储或为开放储位;式(4)表示在任意时刻被搬运的货架必须被指派,且只能指派到一个储位;式(5)表示在任意时刻开放储位i是否被指派货架;式(6)表示t时刻待搬运的货架必须从t-1时刻的存储位置搬出;式(7)为被搬运货架与指派储位货架关系约束,表示任意时刻被指派的货架总数等于被搬运的货架总数;式(8)~式(9)表示仓库布局动态连续变化关系,t时刻储位i的状态等于t-1时刻储位i的状态减去t时刻该储位被搬出货架的情况,并加上t时刻该储位被搬入货架情况之和;式(10)为变量取值约束。
2 算法设计
DPLR是典型的NP-hard问题,对于大规模DPLR问题,精确方法难以求解,需设计启发式算法。模拟退火(Simulated Annealing, SA)算法因其具有受初始解影响小、全局寻优能力强等特点,被广泛用于求解组合优化问题[16-18]。本文将设计反映仓库动态变化关系的SA-STE(simulated annealing single-t exchange)算法来求解DPLR问题,算法流程如图2所示。

2.1 解的编码
解的编码方式如图3所示,横坐标表示整个拣货周期,纵坐标表示仓库储位,仓库中的储位状态用0或正整数表示,0表示储位为开放储位,正整数为存储在该储位的货架编号。拣货周期t的仓库布局通过该时刻末的仓库布局状态表示,例如在拣货周期t=1,储位1存储2号货架,储位2为开放储位,最后一个储位I存储17号货架。当拣货总周期为T,仓库总储位为I时,解为一个T×I的二维数组,反映了整个拣货周期内仓库布局状态的连续变化关系。

2.2 初始解生成
由式(8)可知,周期t时刻的仓库布局与t-1时刻的仓库布局存在关联性(如图4),当拣货周期t=5,9和17号货架若在该时刻未被搬运,其所在的储位状态应与t=4时刻末的储位状态相同,其储位仍为3和I;同样,t=6时,若货架1、9、56和7未被搬运,则其所在储位1、3、I-2和I-1的状态与t=5时刻末的储位状态一致,其他时刻的仓库布局关联关系以此类推。

为使DPLR初始解满足式(8)描述的仓库布局的连续变化关系,SA-STE算法初始解生成步骤如下:

步骤2生成一个在[1,L]区间内的1×I的数组,并使其满足约束(2)~约束(5)。

步骤4l=l+1,若l∉Ωt且l≤L,则转步骤3;若l∈Ωt,则重新执行步骤4,若l>L,则转步骤5。
步骤5令l=1,t=t+1,若t≤T,则转步骤 2,否则结束。
2.3 邻域搜索
本文提出单时刻交换(Single-t Exchange, STE)规则用于候选解的生成,STE规则生成新的候选解分为以下3步:①在拣货周期[1,T]内随机产生一个拣货时刻t;②在该时刻随机选择两个储位;③交换这两个储位中的存储内容(货架)。根据储位中存储内容的不同,存在货架—货架、货架—空位以及空位—空位3种类型的交换方式,如图4所示,根据STE规则先随机产生一个拣货时刻t=3,并在该时刻随机选择两个交换储位,若为(10,14),则是货架—货架的交换方式;若为(15,18),则是货架—空位的交换方式;若为(19,25),则为空位—空位的交换方式。
由于仓库布局存在时序关联性,交换产生的新解可能会打破这一关系,产生不合理的解。为此需要进行解的修复,具体可分为向前修复(Forward Repair, FR)和向后修复(Backward Repair, BR),其中FR为向时间递减方向修复,BR为向时间递增方向修复。不合理解的修复过程如图5所示,当拣货周期t=5,随机产生两个交换储位14和20,对其中存储的1号货架和21号货架进行储位交换,若1号或21号货架在该时刻或下一时刻都未被搬运,则在t=4(FR)或t=6(BR)时刻,14和20号这两个储位也应交换存储内容(双箭头弧形曲线所示),直至交换储位的所有货架与其上一时刻/下一时刻不存在位置继承(被搬运)或t=0/t=T为止。

SA-STE算法领域搜索及不合理解修复步骤如下:


步骤3若在a时刻存在货架—货架或货架—空位的交换,并且存在交换货架不属于Ωa,则令m=a-1,转步骤4;若在a时刻存在货架—货架或货架—空位的交换,并且存在交换货架不属于Ωa+1,则令n=a+1则转步骤5。


3 数值实验
仓库布局及实验参数参考文献[1]和文献[14]设定如下:①平均订单规模为10,拣货总周期为8小时;②货架总数为仓库储位总数的80%,即L=I×80%,并且SKU总数等于L;③需求关系服从20/80规则,即20%的SKU产生80%的订单销量;④仓库储位总数I分别取60,600,800,1 000,1 200;⑤总订单量(Order Quantity, OQ)分别取60,300,600,1 200,2 400,3 600。算法参数如表3所示,利用MATLAB R2014a编程实现,运行环境Win10、64bit操作系统、8 GB内存。

表3 算法参数设定
DPLR问题的求解规模取决于仓库规模(Warehouse Size,WS)和总订单量OQ,其中仓库规模WS又由储位规模(I)和货架规模(L)决定,因此,DPLR的问题规模可表示为(I,L,OQ)。
3.1 算法收敛性验证
在初始仓库布局、SKU需求频率以及客户订单数据相同的情况下,分别利用CPLEX和SA-STE对规模为(60,48,1200)和(600,480,1200)的DPLR问题进行求解,结果如表4所示。
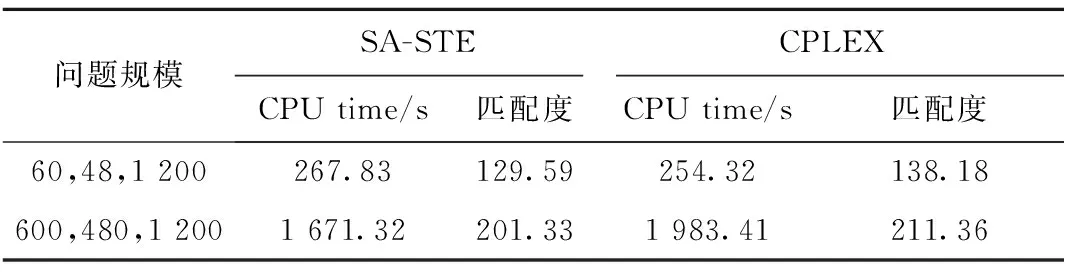
表4 SA-STE算法收敛过程
由表4可知,当问题规模为(60,48,1 200)时,SA-STE和CPLEX分别耗时267.83 s和254.32 s,货架与储位匹配度值(简称“匹配度”)分别为129.59和138.18;当问题规模为(600,480,1 200)时,SA-STE和CPLEX分别耗时1 671.32 s和1 983.41 s,货架与储位匹配度值分别为201.33和211.36。SA-STE算法求解两种问题规模的收敛过程和CPLEX的求解结果对比如图6所示,这表明不同规模的DPLR问题,SA-STE都能在较短时间内实现平稳收敛,并能找到与CPLEX求解结果相近的解,从而表明SA-STE算法在求解质量和计算时间方面都能满足实际要求。

3.2 算法性能分析
分别对4种仓库规模WS和6种订单量OQ进行组合实验,总共24(4×6)种场景。考虑到随机因素,对每种实验场景运行10次取平均,结果如表5所示,其中求解差距为SA-STE的解与CPLEX最优解的比值。

表5 不同问题规模下的实验结果

续表5
如图7所示为SA-STE算法的性能分析结果,分别从收益和计算时间两个方面与CPLEX进行比较。由图7a可知,在任意仓库规模下,订单量越大,SA-STE的求解结果越接近CPLEX最优解;并且在订单量相同的情况下,随着仓库规模增大,SA-STE的求解结果相比CPLEX最优解差距均未超过10%(以订单量2 400和 3600为例),这说明针对大规模的DPLR问题,SA-STE的求解质量可靠。
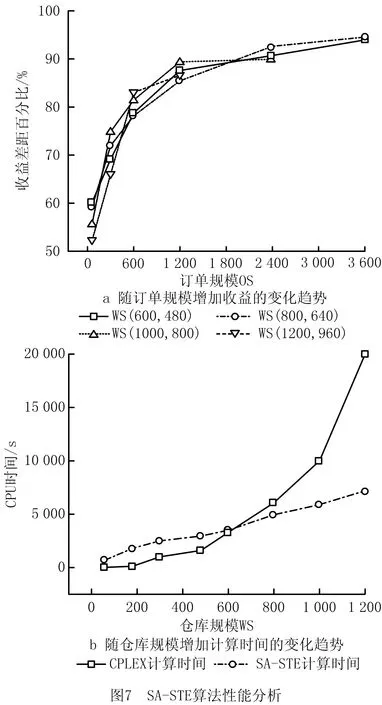
由图7b可知,在订单量较大(2 400和3 600)的情况下,随着仓库规模的增大,CPLEX的计算时间出现了指数爆炸增长,在仓库规模为(1 200,960)的情况下,CPLEX无法在可以接受的时间内求得最优解;但SA-STE的求解时间随着仓库规模的增大变化不大,可以在合理的时间内寻找到接近最优解的可行方案。
由此可知,SA-STE能够求解仓库规模和订单量都较大的DPLR问题,可以在保证解的质量的同时大幅度缩短求解时间。
3.3 DPLR优化效果分析
随机指派(Random Storage, RS)和固定位置指派(Dedicated Storage,DS)策略被广泛用于货位指派优化,在WS为(600,480)的情况下,分别对DPLR与RS、DS的货位指派效果进行对比,结果如表6所示。

表6 DPLR优化效果
初始仓库储位状态热力图如图8所示,右边的色度条表示货架频率,范围为[0,1],货架频率越接近1,表明存储的SKU越畅销。
在不同OQ下,经DPLR优化后的仓库储位状态热力图如图9所示。
由表6、图8和图9可知:相比RS和DS,DPLR可缩短30%左右的货架搬运距离,能有效地提高RMFS的拣选效率;在仓库规模一定的情况下,订单量越大,DPLR的优化效果越显著,即存储畅销SKU的货架被更大概率的指派到靠近拣货站台的区域(即图9中右侧红色区域)存储,这说明了本文提出的模型和算法可以实现仓库存储结构与SKU需求模式相匹配的优化效果,适合订单量和需求波动性巨大的电商、超市以及工厂等企业的RMFS动态货架储位再指派优化。


4 结束语
本文研究了RMFS的DPLR问题,在考虑仓库布局动态连续变化的情况下构建了以货架与储位匹配度为优化目标的混合整数规划模型,并设计了SA-STE算法对大规模DPLR问题进行求解。结果表明,SA-STE算法能在较短时间内求得接近CPLEX的解,通过与传统指派策略比较发现,本文提出的模型和算法可以实现仓库存储结构与SKU需求模式相匹配的优化效果,有效地降低了机器人搬运距离,提高了拣货效率。
当畅销SKU货架被指派到靠近拣货站台的区域存储时,可能会出现搬运机器人在该区域的交通拥堵。因此,考虑机器人行走路径和拥堵情况的DPLR问题有待进一步研究。
