武汉地区某地铁车站深基坑变形规律分析
2021-05-07徐杨青
周 涛,徐杨青
(1.武汉工程大学 土木工程与建筑学院,湖北 武汉 430205;2.中煤科工集团 武汉设计研究院有限公司,湖北 武汉 430064)
随着城市地下空间的不断开发利用,基坑开挖深度越来越深,开挖面积也越来越大;越来越多的超深基坑、超大基坑,各种特殊岩土介质(如长江一级阶地、滨海地区高承压水头及富水地层,深厚软土、黄土及膨胀性岩土地层)和各种严峻环境条件下地铁建设中的深基坑工程更是给广大岩土工程技术人员带来了前所未有的挑战,深基坑工程问题也越来越多,成为工程建设中的难点、热点问题[1-3]。同时,由于地铁基坑多数位于城市中心,建设场地周边环境复杂。鉴于此,已有不少学者通过数值软件来模拟研究地铁深基坑开挖对周边环境及基坑本身的影响。例如,谢乐等[4]采用Midas软件建立地铁车站三维模型,针对基坑不同围护型式进行敏感性分析,研究表明围护桩+内支撑支护型式对基坑变形有较强的限制作用;高彦斌[5]通过监测数据对基坑立柱隆起进行分析,结果表明基坑开挖方式和底板浇筑工序对立柱隆起有较大影响,且基坑立柱隆起具有明显的空间效应;郭抗美等[6]依托天津某软土地区深基坑工程,对基坑开挖过程进行监测,并利用FLAC 3D软件对基坑开挖支护进行模拟,得到了最大侧向位移的公式;岳云鹏等[7]通过三维有限元模型,研究分块开挖基坑对下卧盾构隧道保护的有效性,结果表明分块数量越多对隧道竖向位移控制效果越好;郜新军等[8]通过有限元分析方法,分析了深基坑开挖过程中邻近管线的位移变化规律,提出了注浆法、微型桩法及二者联合的三种管线加固措施,结果表明二者联合方法可很好地控制管线的水平及竖向位移。本文以武汉地铁某车站深基坑工程为背景,结合土体开挖过程中基坑监测数据,利用Midas GTS NX软件建立车站深基坑的三维数值仿真模型,对基坑的开挖和支护施工过程进行模拟,对比研究数值仿真计算结果与监测数据,总结深基坑工程在施工过程中的变形规律。
1 工程概况
1.1 车站基本情况
拟建车站为地下两层米岛式车站。车站总建筑面积17 609.8 m2,标准段宽21.3 m,车站主体基坑开挖深度20.49~23.49 m,开挖面积5 347 m2,车站采用明挖法施工,主体采用钢筋混凝土箱型结构,围护结构采用钻孔灌注桩+五道内支撑。围护桩布置方案为1 000 mm@1 200 mm,插入深度36 m。基坑支护及监测平面图如图1所示。
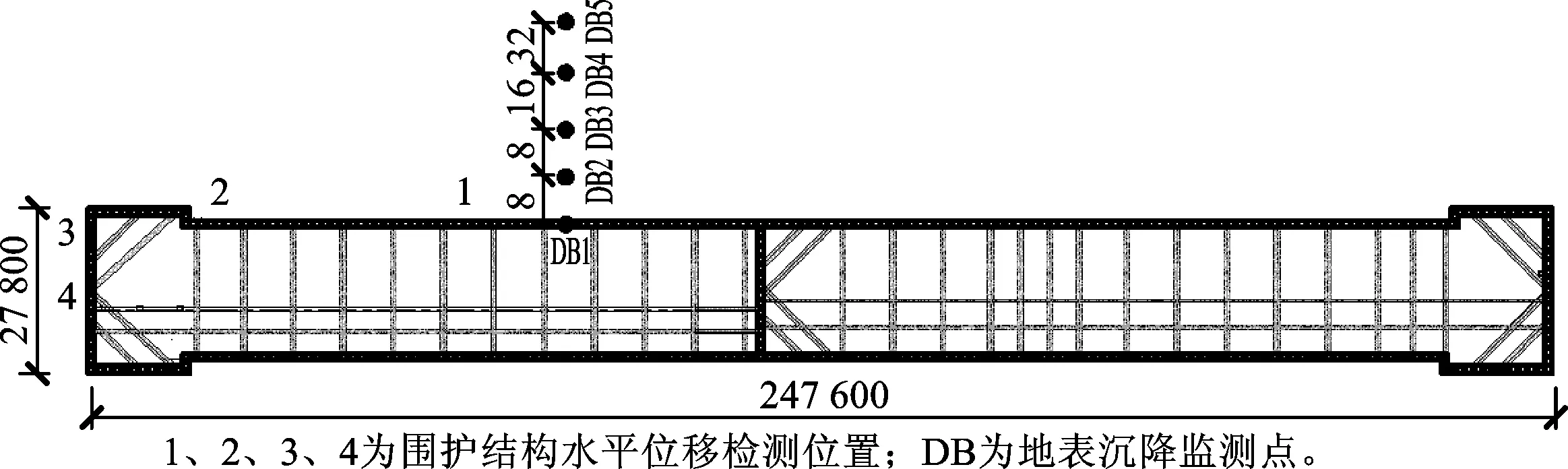
图1 基坑支护及监测平面图Fig.1 Plan of foundation pit support and monitoring
1.2 场区地质条件
车站地貌单元主要为剥蚀堆积垄岗状平原(长江Ⅲ级阶地),局部为湖泊堆积平原(长江Ⅱ级阶地)、剥蚀丘陵区。场地覆盖层主要有人工填土、第四系粉质粘土、长江古河道地层。各岩土层工程特征情况如下:

2 基坑监测
根据基坑支护结构型式及周边环境,本项目主要对周边地表沉降、围护结构水平位移和支撑轴力进行监测。由于本文篇幅有限,仅对部分围护结构水平位移和地表沉降进行分析。
3 基坑有限元模型建立
采用有限元软件Midas GTS NX建立基坑模型,对基坑开挖和支护各阶段进行模拟分析[9]。从图1可知,拟建车站基坑为长条形,由勘察报告可知,地层分布沿车站纵向起伏不大,按各土层水平建模,基坑所处地层自上而下分别为杂填土、粘土、粉土、粉细砂、砂岩,各土层厚度和物理参数见表1。同时,场地1~2倍基坑深度范围内无建筑物和对分析造成明显影响的外荷载,基坑标准段宽为21 m,开挖深度取22 m,考虑边界效应的影响,土体模型尺寸沿基坑水平方向取4倍的基坑开挖深度,沿深度方向取3倍的基坑开挖深度。因此模型尺寸为360 m×184 m×65 m,将围护桩按刚度等效成地下连续墙,采用板单元模拟、混凝土支撑,钢支撑采用弹性本构、梁单元模拟,土体采用修正摩尔库伦本构,修正摩尔库伦本构采用不同的加荷与卸荷模量,能够反映土体应力路径的影响,比较适合用于基坑开挖数值分析[10]。支护结构材料参数见表2,有限元模型如图2。为考虑施工开挖和支撑架设的动态性,对不同开挖过程建立如下六种工况:

图2 有限元模型图Fig.2 Model diagram of finite element

表1 土层参数表Table 1 Table of soil parameters
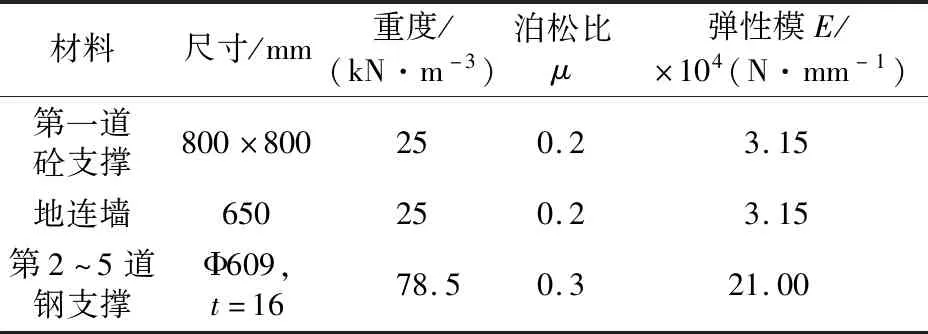
表2 支护结构材料参数表Table 2 Material parameters of supporting structure
工况一围护结构施工,基坑开挖至-0.6 m,设置第1道混凝土支撑;
工况二基坑开挖至-7 m,设置第2道钢支撑;
工况三基坑开挖至-11.4 m,设置第3道钢支撑;
工况四基坑开挖至-15.9 m,设置第4道钢支撑;
工况五基坑开挖至-17.4 m,设置第5道钢支撑;
工况六开挖至坑底,即-22 m。
4 模拟值与监测值比较
4.1 地下连续墙变形分析
通过提取墙体水平位移模拟结果,图3为断面1位置,从图中可以看出,在基坑开挖初期,如工况一条件下,基坑开挖深度较浅,水平变形的最大位置出现在围护墙的顶端,而在墙底部水平位移值趋于0,曲线呈现出上大下小“三角形”形状。围护结构的水平位移实测曲线和模拟曲线两者变形趋势基本一致。随着基坑施工进行,开挖深度不断增大,围护结构的变形不断增加,模拟值与实测值差值逐渐增加,当基坑开挖结束后,围护结构达到最大变形,实测结果比模拟结果大5 mm,但最大水平位移的位置均随着开挖深度的增加逐渐向下移动,最大位移值在基坑开挖面附近。
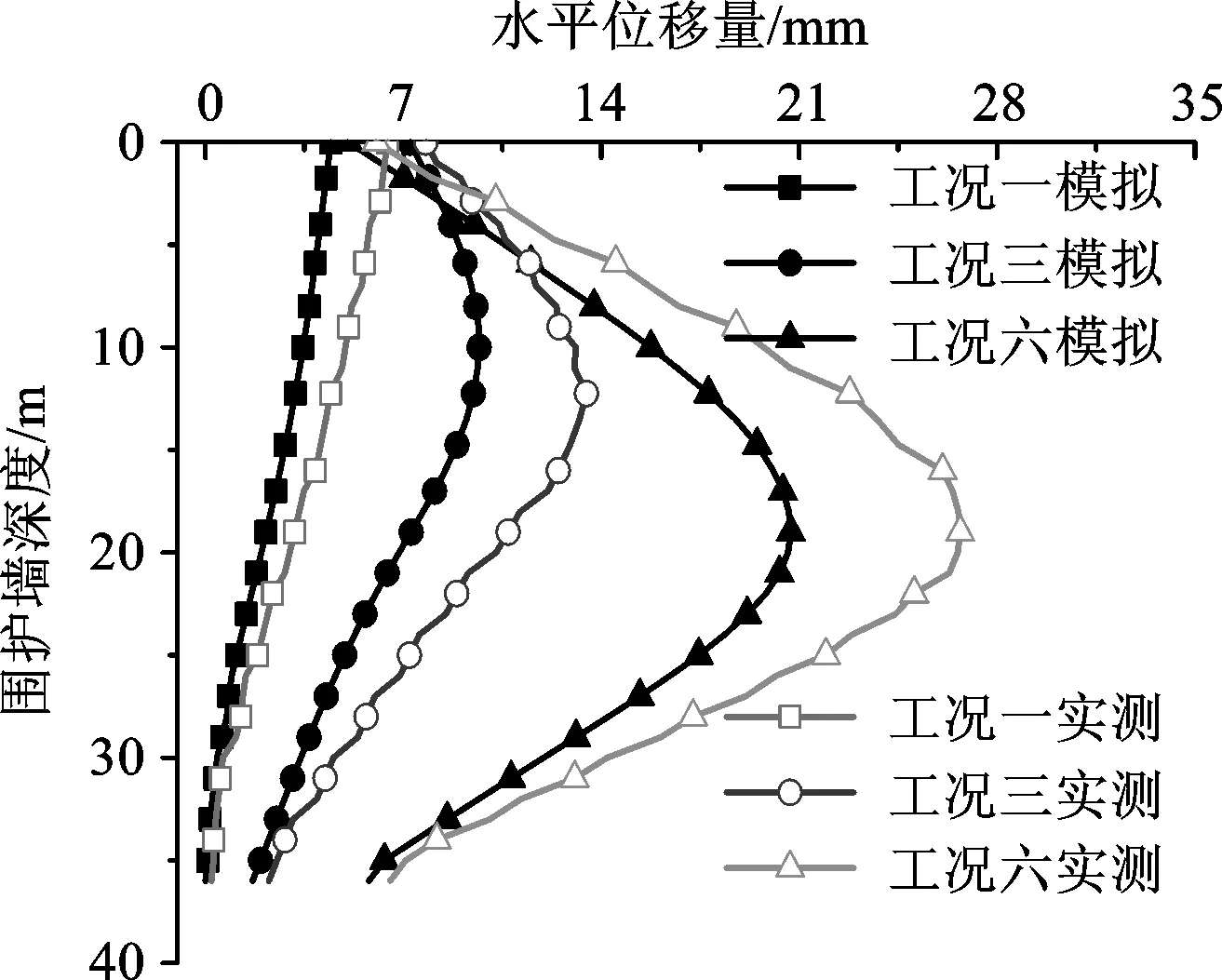
图3 断面1围护墙变形图Fig.3 Deformation of the retaining wall at position 1
图4为基坑沿长边方向断面2位置的围护墙水平变形曲线。该位置的围护结构水平变形与断面1的规律类似,但模拟值和实测值都略小于断面1,基坑开挖结束后,模拟值最大值较断面1减小约12%,实测值减小8%。从图1可以看出,断面2更接近基坑角部位置,基坑角部位置提供的约束作用增强,因此导致其水平位移小于基坑中部的水平位移。

图4 断面2围护墙变形图Fig.4 Deformation of the retaining wall at position 2
图5、图6为基坑沿短边方向上的围护墙水平变形曲线。从图5-图6可以看出,断面4围护结构水平变形规律和断面3变形规律基本一致,同时基坑短边方向变形规律与基坑长边方向变形规律也基本类似。对于实测值和模拟值,在各工况下,断面3墙体水平位移明显小于断面4墙体水平位移,这是因为断面3位于坑角,其受约束作用更强,因此其水平变形小于断面4水平变形。

图5 断面3围护墙变形图Fig.5 Deformation of the retaining wall at position 3

图6 断面4围护墙变形图Fig.6 Deformation of the retaining wall at position 4
由上述曲线可以看出,随着基坑开挖的进行,对于基坑的长边和短边,当开挖较浅时,围护墙的变形均较小,其时空效应不太明显。随着基坑开挖深度的增加,围护墙的变形逐渐增加,时空效应越来越明显。此外,对于基坑长边,围护结构水平位移实测值大小和模拟值略微有差距;对于基坑短边,实测值和模拟值吻合度较高。基坑长边方向的围护结构水平变形大于短边方向,跨中部位的变形大于端部拐角部位。因此,基坑短边的时空效应较明显,长边的空间作用较弱;且基坑端部作用明显,基坑跨中部位的作用较弱。基坑具有三维的特点,而二维分析则无法体现基坑的这种特点。
4.2 基坑周边土体沉降分析
图7为开挖一至开挖六施工过程的坑外土体沉降曲线。整体来看,采用软件能够较好地模拟基坑开挖引起的周边地表沉降,模拟结果表明,墙后地表沉降符合凹槽型分布模式,符合内撑式基坑开挖变形特点,地表沉降随基坑开挖深度的增加而增加;在工况三条件下,对坑外地表沉降进行不间断监测,每隔24 h读取一次监测值,沉降随时间变化曲线如图8所示,由图可知,在基坑开挖深度不变条件下,随着施工进行,各监测点沉降值不断改变,但总体变化趋势基本一致,均呈现凹槽型,当基坑刚开挖结束,沉降实测值为9 mm,模拟值为12 mm,实测值略小于模拟值。但随着时间的推移,周围土体受扰动后在第10天重新达到稳定状态,地表沉降稳定在15 mm,比模拟值大3 mm。因此,在基坑开挖过程中,控制施工速率,减少基坑暴露时间,及时架设支撑以避免周边土体的不可逆塑性变形的积累。施工时在此范围内的建筑(构)物、地下管网应加强监测,保证基坑的安全,减少对周边环境的影响[11]。
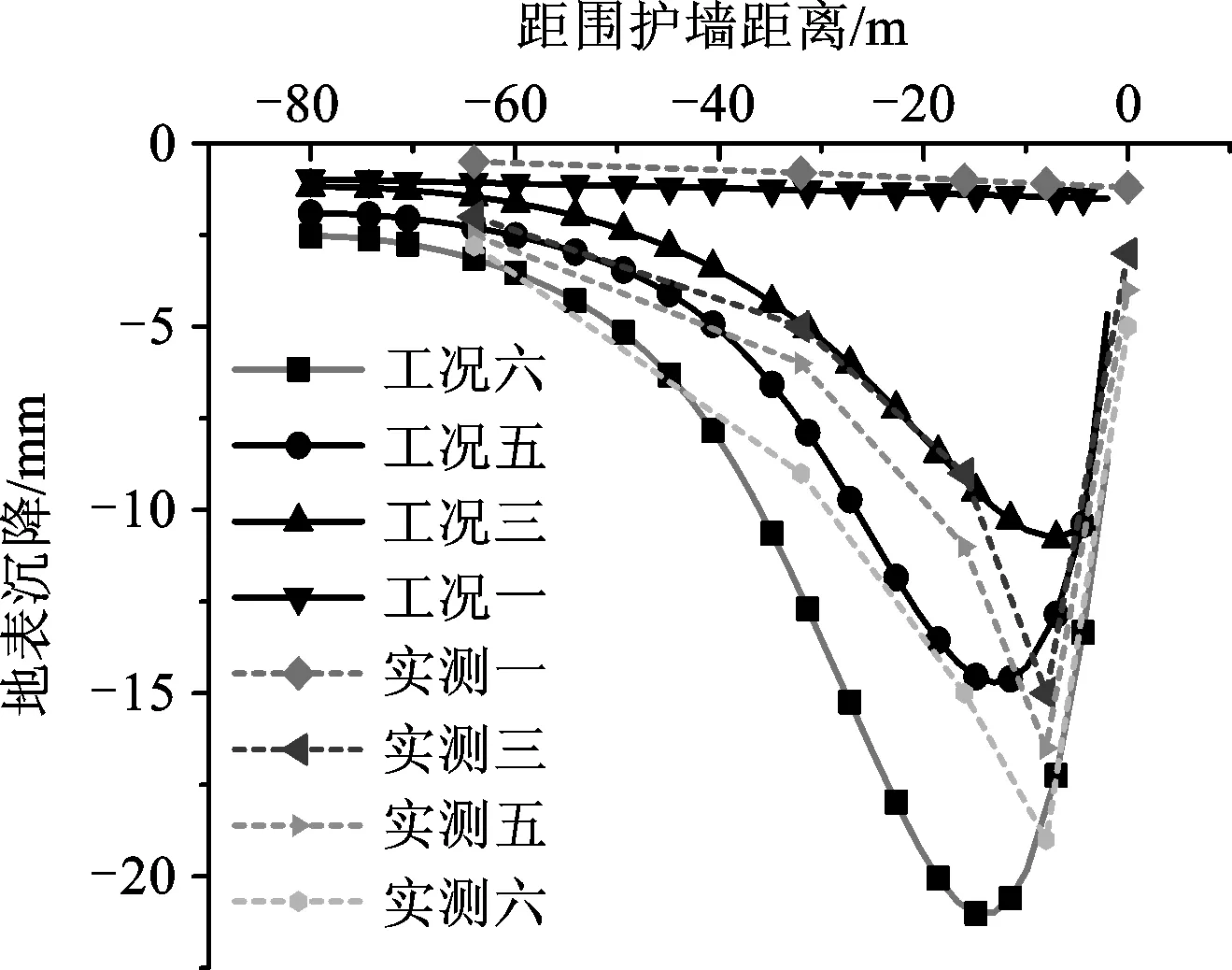
图7 坑外地表沉降曲线Fig.7 Surface settlement curve outside the pit

图8 工况三坑外地表沉降变化曲线Fig.8 Change curve of surface settlement outside the three pits under workingcase Ⅲ
5 结论
(1) 围护墙水平变形数值模拟规律与监测规律基本吻合,四个断面墙体位移均沿着墙身先增大后减小,最大变形处均在基坑开挖面附近,符合基坑开挖特征。
(2) 围护墙最大水平变形发生在基坑长边且为跨中部位,其中短边方向变形较小,且基坑角部变形最小。
(3) 地表沉降曲线近似呈凹槽型,坑外土体受基坑开挖的影响范围主要在基坑边1~2倍基坑深度范围内,且地表沉降随基坑开挖深度的增加而增加,与数值模拟沉降规律基本一致。
(4) 在同一工况下,随着时间的推移,不同位置监测点的位移值呈现不断重分布的过程,但整体曲线仍大致呈凹槽型。
