基于蒙特卡罗法的乌江特大桥边坡稳定性可靠度分析
2021-05-07谢玉洁
谢玉洁
(1.河南省地质调查院,河南 郑州 450001;2.河南省地球化学生态修复工程技术研究中心,河南 郑州 450001)
边坡稳定性问题是工程建设中十分常见的问题,需要重视。目前在边坡工程设计中,常采用稳定性系数法评价边坡稳定性[1-2],但忽略了实际工程地质环境中的变异性和不确定性。若在边坡工程设计中充分考虑这些不确定因素,则能够更加贴近工程的实际稳定性状态。基于可靠度理论,可对边坡稳定性状态作出准确判断,该方法已广泛应用于工程实践中[3]。本文以翁马铁路乌江特大桥岸坡为例,基于蒙特卡罗法(Monte Carlo Method),借助边坡稳定性分析软件Geo-studio的Geo-Slope模块对桥址区的边坡稳定性进行可靠度分析。
1 计算原理
蒙特卡罗法是以概率统计抽样理论为基础,研究随机变量的计算方法。
设功能函数为:
z=g(x1,x2,…,xn)
(1)
式中:xi(i=1,2,…,n)为任意分布的随机变量。
对xi进行N次抽样,得到N组xij(i=1,2,…,n;j=1,2,…,N)样本。将第j组的值代入功能函数(1)得到zj值,如果N个zj值中有M个zj≤0,则当N→∞时,根据伯努利大数定理,可用频率值等同于概率值,因此破坏概率为:
(2)
影响边坡稳定性的不确定因素有很多,本文以岩土参数作为随机变量来分析边坡可靠度[4]。依据安全储备和边坡岩土体参数变量之间的关系建立极限状态方程:
z=g(x)=Fs-1=Fs(C,φ)-1
(3)
式中:内摩擦角φ和粘聚力C为随机变量,安全系数Fs由φ和C迭代产生。
极限状态方程(3)随随机变量变化出现三种不同的结果,即:
(1)z>0,此时边坡处于稳定状态,用可靠度表示;
(2)z=0,此时边坡处于极限平衡状态;
(3)z<0,此时边坡存在失稳的可能性,用破坏概率Pf表示。
利用式(3)求解出N组z值。设z<0的个数为M,则边坡破坏概率为:
(4)
相应的边坡稳定性可靠度为:
β=f-1(1-Pf)
(5)
2 计算方法和过程
边坡稳定性软件Geo-studio的Geo-Slope模块可进行临界破坏面的自动搜索,在不同条件下确定边坡临界安全系数,以求得的安全系数来评价坡体的稳定状态[5-6]。
Geo-Slope软件使用蒙特卡罗法进行边坡可靠度分析,同时利用极限平衡法求解最小安全系数。具体求解步骤为:
(1) 确定最危险滑面。给出内摩擦角φ和粘聚力C的取值范围,利用Geo-Slope软件建立岸坡模型,以岸坡内摩擦角均值φo和粘聚力均值Co作为参数进行计算,确定岸坡最危险滑面,并得到均值安全系数Fso;
(2) 随机抽样模拟计算安全系数Fs。确定随机抽样数N,调整内摩擦角φ和粘聚力C参数取值,利用Geo-Slope软件在已确定的最危险滑面上进行模拟,计算得出安全系数Fs。
(3) 计算边坡破坏概率Pf和可靠度指标β。对模拟得到的安全系数Fs进行统计,得到<1的Fs的个数M及其安全系数均值μFs和标准差σFs,进而采用公示(4)和(5)计算出边坡可靠度指标β和破坏概率Pf。
3 工程实例分析
瓮马铁路乌江特大桥位于乌江河谷(图1),该河谷为深切“V”型谷,两岸岸坡陡峭,地形条件复杂,两岸相对高差约60 m。右岸自然坡度为54°~80°,坡脚至坡顶高程为478~878 m,岸坡高差为400 m,坡脚至坡顶水平距离为258 m。两岸植被覆盖茂密,局部地区基岩裸露。岸坡体基岩岩层均为古近系砾岩,呈巨厚层状—块状,岩性主要为灰岩,局部卸荷裂隙发育。

图1 乌江特大桥右岸剖面图Fig.1 Profile of right bank of Wujiang grand bridge1.砾岩;2.剖面方向;3.滑动面;4.结构面;5.水位;6.岩层产状。
乌江特大桥两岸岸坡结构面结合程度一般,按照结构面抗剪强度参数取值标准[7]来看,其内摩擦角φ取值范围为35°~27°,粘聚力C取值范围为0.13~0.09 MPa。综合考虑现场结构面结合程度,确定乌江特大桥岸坡整体上的内摩擦角均值为35°,粘聚力均值为0.13 MPa,岩体重度取值为26 kN/m3。
基于概率统计理论,要统计分析大量的试验数据来确定抗剪强度参数的不确定性,可用样本的均值μ和标准差σ来表示不确定性,其中:
(6)
(7)
式中:μ为参数均值;σ为参数标准差;n为统计样本个数。
由于标准差σ需要大量的数据来确定,而实际工程中常常无法满足要求,因而引入参数变异系数δ表征参数的离散性,即:
(8)
国内外学者依据已有工程试验数据,对岩体抗剪强度参数进行了详细研究,给出了相应的变异系数δ推荐取值范围(表1),并指出岩体弱结构面的内摩擦角和粘聚力具有相似统计特性,即:内摩擦角明显服从正态分布,变异系数大多为0.05~0.4;粘聚力基本服从正态分布,变异系数一般为0.2~0.5。通常情况下,岩体的变异性多为低—中等,因此本文取内摩擦角变异系数δφ为0.1~0.3,粘聚力变异系数δc为0.2~0.3,且在计算中不考虑二者的相关性[5]。

表1 岩土性质指标变异性取值Table 1 Variability value of geotechnical property index
以乌江特大桥右岸岸坡为研究对象,选取桥基所在剖面为计算剖面,利用Geo-Slope软件建立右岸岸坡模型,以参数均值μo、Co并进行计算,确定了岸坡最危险滑面(图2),计算得到参数均值安全系数Fso=1.181。
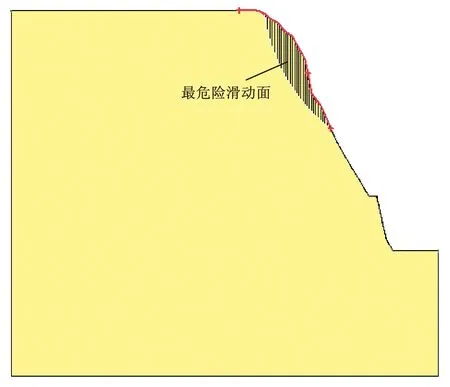
图2 乌江特大桥右岸岸坡计算模型Fig.2 Calculation model of right bank slope of Wujiang bridge
然后在天然状态下进行了10 000次的蒙特卡洛随机模拟,经过拟合后,安全系数Fs频数均明显呈正态分布(图3)。
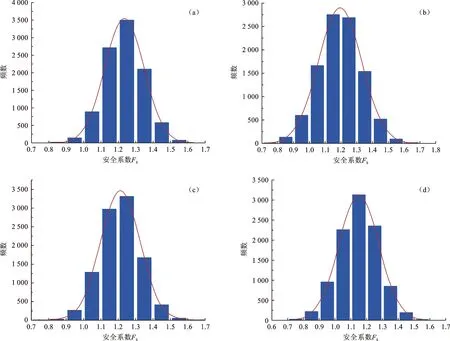
图3 安全系数Fs频数分布Fig.3 Frequency distribution of safety factor Fsa.δc=0.2,δφ=0.1;b.δc=0.2,δφ=0.3;c.δc=0.3,δφ=0.1;d.δc=0.3,δφ=0.3。
在工程结构设计时通常会留有一定安全裕度,以应对一些偶然荷载突增的突发状况,由此提出目标可靠度的概念。目标可靠度是指工程结构满足要求的最低标准,本文采用的目标可靠度取值范围为2.32~2.75。
由表2和表3可知,当δc=0.2,δφ=0.1时,Pf=1.58%,岸坡处于稳定状态;β=2.147,岸坡处于不可靠状态。当δc=0.2、δφ=0.3时,Pf=7.57%,岸坡处于基本稳定状态;β=1.440,岸坡处于不可靠状态。当δc=0.3、δφ=0.1时,Pf=2.96%,岸坡处于稳定状态;β=1.902,岸坡处于不可靠状态。当δc=0.3、δφ=0.3时,Pf=11.95%,岸坡处于基本稳定状态;β=1.902,岸坡处于不可靠状态。
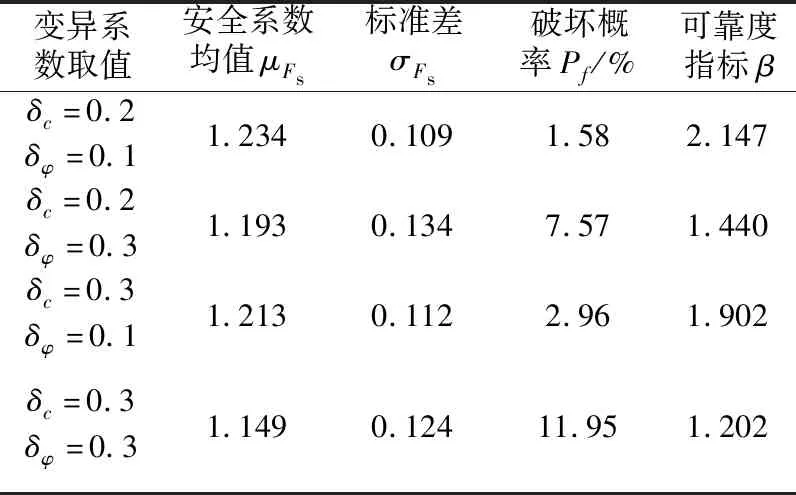
表2 可靠度分析结果Table 2 Reliability analysis results

表3 稳定程度与破坏概率的关系Table 3 Relationship between stability and failure probability
4 结论
本文基于蒙特卡罗法开展了乌江特大桥右岸边坡稳定性可靠度分析,表明当抗剪强度按确定值计算时,乌江特大桥右岸岸坡整体安全系数为1.181,岸坡处于稳定状态,但安全储备不足;当以抗剪强度为随机变量时,破坏概率为1.58%~11.95%,岸坡处于基本稳定状态;可靠度为1.202~2.147,岸坡处于不可靠状态。因此岸坡整体处于稳定状态,不会发生大规模失稳破坏,仅岸坡上部较陡处处于欠稳定—基本稳定状态。
