基于径向剪切干涉仪的三维位移测量技术*

王佳 刘荣明 王佳超 吴慎将

(西安工业大学光电工程学院, 西安 710021)

本文提出一种基于双圆光栅径向剪切干涉仪的三维位移测量方法, 其测量原理是径向剪切干涉仪所形成的莫尔条纹不仅由二维平面内位移决定, 轴向位移会在+1 和–1 级莫尔条纹之间产生一个特定的相移.首先, 基于标量衍射理论对双圆光栅径向剪切干涉仪的+1 和–1 级莫尔条纹强度分布进行推导, 建立了三维位移量与莫尔条纹强度分布的精确解析关系; 其次, 在频谱分析的基础上, 利用半圆环滤波器进行空间滤波, 实现+1 和–1 级莫尔条纹的同时成像; 然后, 提出了从莫尔条纹图中定量提取三维位移的算法, 并通过数值模拟进行验证; 最后, 实验结果验证了该方法测量平面内位移的最大绝对误差为4.8 × 10–3 mm, 平均误差为2.0 ×10–4 mm, 轴向位移的最大绝对误差为0.25 mm, 平均误差为8.6 × 10–3 mm.该方法具有装置简单、测量精度高、非接触、瞬时测量等特点, 可实现三维位移的同时测量.

1 引 言

两个周期性的光栅重叠可以产生莫尔条纹, 这种莫尔现象在表面形貌、位移、应变、振动和折射率等光学测量领域有着广泛的应用[1−8].在位移测量方面, 莫尔条纹技术具有精度高、装置简单、测量范围大等特点, 已广泛应用于二维位移测量[9−11].利用直线光栅的莫尔条纹可以测量二维平面内的偏转角和一维位移[12].随着精密测量要求和光栅制造精度的提高, 利用圆光栅莫尔条纹的二维位移测量得到了较深入的研究和应用[13−16].利用傅里叶变换算法、图像分析算法或基于强度的计算方法可以从莫尔条纹中定量提取出位移信息[17,18].但是, 它们仅适用于二维平面内位移的测量, 不能实现包含轴向位移的三维位移量测量.

基于几何叠加理论的研究表明, 圆光栅的莫尔条纹对平面内位移以及轴向位移均敏感[19,20].当两个光栅之间存在轴向距离时, 从不同角度观察到的莫尔条纹图案不同.基于该原理的三维位移测量要求采集不同角度的莫尔条纹图像, 在测量过程中需要移动探测器或使用多个探测器, 探测器位置会引入新误差[20].除此之外, 没有文献报道利用圆光栅莫尔条纹进行三维位移测量.

对两个完全相同的圆光栅进行径向剪切干涉的研究表明, 每个衍射级次的莫尔条纹与光栅圆心间的三维位移有关[21].特别地, +1 和–1 级莫尔条纹之间存在一个依赖于两个光栅之间轴向距离的相移量.如果同时对+1 和–1 级莫尔条纹进行成像,则可实现三维位移的测量.然而当平面内位移量都为0 时, 具有两个完全相同圆光栅的径向剪切干涉仪不会产生莫尔条纹, 无法实现三维位移的测量.本文提出利用两个参数不同的圆光栅径向剪切干涉仪的三维位移测量技术.建立并分析了测量系统, 得到三维位移与莫尔条纹强度的精确解析关系, 并提出了三维位移量提取算法.数值仿真和实验验证了该方法的可行性和精度.

2 测量原理

双圆光栅径向剪切干涉仪的光路如图1 所示.G1 和G2 是两个Ronchi 同心圆光栅, 其占空比为1, 周期分别为a1和a2.两个光栅平面相互平行并垂直于光轴放置.光栅G1 的圆心固定在z轴上,光栅G2 与被测位移物体相连, 被测物体的三维位移量决定了G2 圆心的空间位置.两个光栅圆心在(x,y) 平面内的位移如图2 所示, 其中∆x和∆y分别表示x轴和y轴位移, 轴向位移由∆z表示.L1和L2 为傅里叶变换透镜, 与空间滤波器F 组成4-f系统, 用于对不同衍射级次的莫尔条纹图像进行滤波和成像.

图1 双圆光栅径向剪切干涉仪光路图Fig.1.Schematic diagram of radial shearing interferometer with double circular gratings.

图2 两个光栅圆心在 ( x,y) 平面内的二维位移Fig.2.The geometric relation of in-plane displacements for two gratings.

在极坐标系 (r,φ) 中, 圆心在z轴上的光栅G1 的透过率函数g1(r,φ) 可以表示为

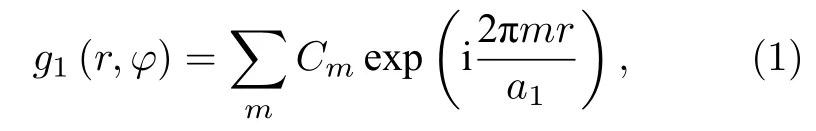
其中m表示光栅G1 的衍射级次,为傅里叶展开系数.准直单色平行光入射到G1 上,则G1 后表面的光场分布为

根据标量衍射理论, 入射光经过G1 后的传播可以由惠更斯-菲涅尔-基尔霍夫积分表示[22], 传播轴向距离∆z后光栅G2 前表面的光场分布为

其中M为一个常数.

由于G2 的圆心在x和y方向的位移为∆x和∆y, 如图2 所示, 则G2 上的点 (r2,φ2) 在 (r,φ) 坐标系中的位置为

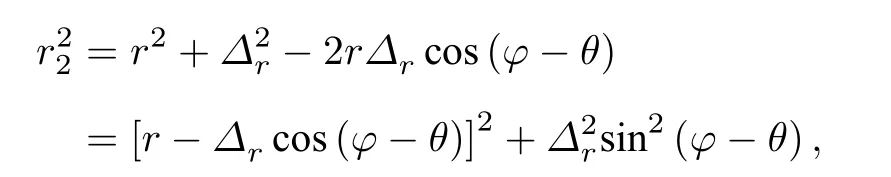
由于∆r →0 , 因此r2=r −∆rcos(φ −θ) , 则光栅G2 的透过率函数可以表示为

其中n表示光栅G2 的衍射级次, 傅里叶展开系数Cn=(1/2)sinc(nπ/2), 并且

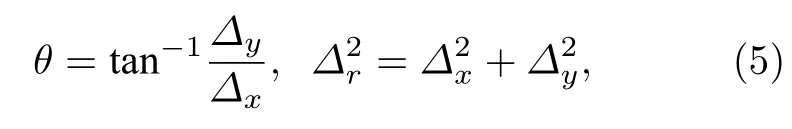
因此, 光栅G2 后表面的光场分布为

图3 用几何方法描述了入射光经过两个圆光栅的衍射过程.由于圆光栅栅线曲率的中心对称特性, 衍射光传播方向也呈中心对称分布.经过光栅G1 后, +1 级衍射光发散传播, 而–1 级衍射光汇聚传播, 因此相同衍射级次的光的传播方向不再相同.根据角谱理论, 传播方向的相同光具有相同的频谱[22].因此, 同一级频谱中包含了不同衍射级次的光.经过双圆光栅后,m+n=+1 和m+n=−1 级衍射光都包含在一级频谱中, 因此不能利用传统的空间滤波方法对+1 和–1 级衍射光分别进行成像.

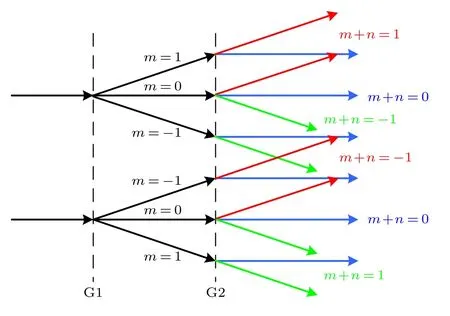
图3 双圆光栅的衍射过程Fig.3.Geometrical schematic of diffraction process by double circular gratings.

很显然, 透射率为中心对称径向周期函数的同心圆光栅的频谱是中心对称分布的.如图4(a)所示, 经过双圆光栅的衍射光频谱由一系列同心圆组成, 相邻频谱的间隔为 1 /a1(a1≈a2).此外, 某一个点的 (m+n) 级衍射频谱与其中心对称点的−(m+n)级衍射频谱处于相同的位置.也就是说,如果将一级频谱沿y=0 分为上、下两个部分, 则成像面将相应地被划分为y>0 和y<0 两个部分.如果使用图4(b)中的半圆环形空间滤波器使φ ∈[0,π) 部 分的一级光谱通过, 则成像面上y >0部分为m+n=+1 级衍射光成像,y<0 部分为m+n=−1 级衍射光.相反, 如果使φ∈[π,2π) 部分的一级光谱通过, 则成像面上y>0 部分为m+n=−1 级 衍射光成像,y<0 部分为m+n=+1 级衍射光成像.因此, 可以在成像面的上、下两部分分别得到+1 和–1 级莫尔条纹图像.

图4 (a)双圆光栅的频谱分布; (b)实验中使用的半圆环形滤波器Fig.4.(a) Spectrum distribution of double circular gratings;(b) the semicircular spatial filter used in experiment.

+1 和–1 级莫尔条纹是由m+n=+1 和m+n=−1 级衍射光成像的结果.当|m|>1 和|n|>1时, 傅里叶展开系数非常小, 因此只需要保留其中(m=1,n=0),(m=0,n=1) 和(m=−1,n=0),(m=0,n=−1)这两项.因此, 成像面光场分布可以表示为

莫尔条纹强度分布表示为

(9)式和(10)式表明: +1 和–1 级莫尔条纹不仅由平面内位移量 (∆r,θ) 决 定, 也受到轴向位移∆z的影响.∆z在+1 和–1 级莫尔条纹之间引入一个相移, 因此会导致莫尔条纹在y=0 处出现突变.

当探测光源为He-Ne 激光(波长为632.8 nm),圆光栅G1 和G2 的周期分别为0.10 mm 和0.11 mm 时, 通过(9)式和(10)式进行数值模拟得到的莫尔条纹如图5 所示.在相同的参数下实验得到的莫尔条纹如图6 所示.可以清楚地看出,数值模拟与实验结果完全吻合, 证明了理论推导的正确性.

图5 数值模拟得到的不同位移量的莫尔条纹Fig.5.Moiré patterns with different 3D displacements obtained by numerical simulation.

3 位移信息提取

3.1 提取算法

从莫尔条纹图中定量提取三维位移信息的方法包括傅里叶变换算法、图像分析算法或基于强度的计算方法[17,18,20].为了方便处理, 一般以莫尔条纹的中心为原点, 将直角坐标系下的莫尔条纹转换到极坐标系中进行分析.

由(9)式和(10)式可以得到+1 或–1 级莫尔条纹的亮条纹中心坐标位置(以下称为特征点)为

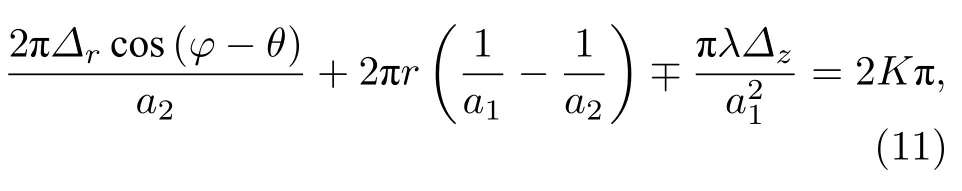
其中当y>0 时符号为“–”, 当y<0 时符号为“+”,K为未知整数.

在+1 级或–1 级莫尔条纹图中同一亮条纹上的特征点P+1={(ri,φi),i=1,2,3,···}或P−1={(ri,φi), i=1,2,3,···}满足关系式:

图6 实验得到的不同位移量的莫尔条纹Fig.6.Moiré patterns with different 3D displacements obtained by experiment.

其中 (ri,φi) 和 (ri−1,φi−1) 是+1 级或–1级中的两个特征点位置.利用三个特征点的位置, 可以得到以下线性方程组:

因此, 平面内位移∆x和∆y可以通过以下公式进行求解:

由(11)式可以得到, 同一条亮条纹中+1 级和–1 级特征点满足关系式:

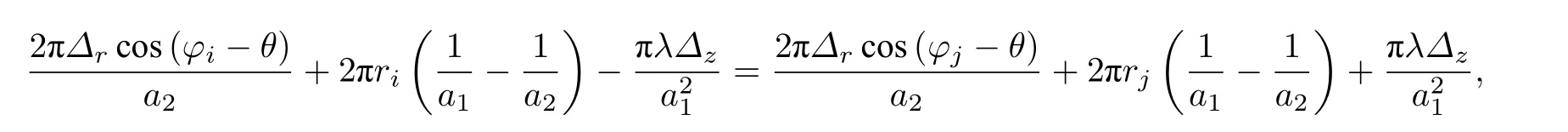
利用+1 级和–1 级同一条亮条纹中的两个特征点位置 (ri,φi) 和 (rj,φj) , 可以求解出轴向位移∆z:

3.2 数值模拟

通过数值模拟实验验证位移提取算法的精度.在模拟实验中, 探测光的波长为632.8 nm, 两个圆光栅的周期分别为0.10 mm 和0.11 mm.通 过(9)式 和(10)式 计 算 出(∆x,∆y,∆z)=(0.2 mm,0.1 mm,4.5 mm)的莫尔条纹如图7(a)所示.

图7 提取特征点坐标的图像处理过程Fig.7.Process of image processing for extracting the coordinates of feature points.

首先, 将直角坐标系中的莫尔条纹转换到极坐标系中, 结果如图7(b)所示.其次, 对图像进行二值化, 并提取出亮条纹的骨架, 结果如图7(c)和(d)所示.然后, 保留其中一个亮条纹骨架, 数值为255 的像素点位置即为亮条纹的特征点位置.最后, 利用(13)—(15)式计算三维位移, 结果为

(0.2003 mm, 0.0999 mm, 4.4417 mm), 绝对误差为0.1521%、0.1404%和1.2965%, 证明了该算法具有较高的精度.

4 实验及分析

实验中光源选用He-Ne 激光器(大恒光电DH-HN250), 探测光波长为632.8 nm.圆光栅G1和G2(苏州聚芯微纳科技有限公司设计加工)的周期分别为0.10 mm 和0.11 mm.光栅G1 的圆心固定于光轴上, 光栅G2 安装在一个分辨率为0.001 mm的三维平移台(大恒光电GCM-TP)上进行平移.4f 系统中傅里叶变换透镜的焦距为150 mm, 孔径为38.1 mm(大恒光电GCL-010607).用CCD 相机(CCD: MER-630-16 GM/C, 镜头: Kowa LM12-JC5MC)采集莫尔条纹, 由于镜头的放大作用, 每个像素的真实成像大小为0.05 mm.

首先对轴向位移测量进行实验研究.保持平面内位移∆x= 0 mm、∆y= 0 mm 不变, 轴向距离∆z以间距1 mm 由0 mm 增加到15 mm, 实验获得的莫尔条纹如图8 所示.利用上述位移提取算法对莫尔条纹进行处理, 得到轴向位移∆z变化如图9(a)所示, 图9(b)显示了轴向位移测量误差.

然后进行三维位移测量实验.实验中位移∆y=0.15 mm 和∆z= 7.90 mm 保持不变,∆x以间距0.05 mm 从0 mm 增加到0.35 mm.实验得到的莫尔条纹如图10 所示.三维位移测量结果及测量误差如图11 所示, 详细数据见表1.

由(13)—(15)式可知, 三维位移测量精度取决于光栅周期、探测光波长和特征点位置精度.测量误差主要由坐标变换原点和亮条纹特征点的定位误差造成的.

实验结果中, 测量平面内位移的最大绝对误差为4.8 × 10–3mm, 平均误差为2.0 × 10–4mm, 轴向位移的最大绝对误差为0.25 mm, 平均误差为8.6 × 10–3mm.在已有的测量方法中, 平面内位移的最大绝对误差为5.25 × 10–3mm[18], 轴向位移的最大绝对误差为0.22 mm, 平均误差为0.085 mm[20],与该方法具有较高的测量精度.

图8 当 Δ x = 0 mm、 Δ y = 0 mm 时实验得到的莫尔条纹图Fig.8.Moiré patterns captured by experiment when Δ x = 0 mm and Δ y = 0 mm.

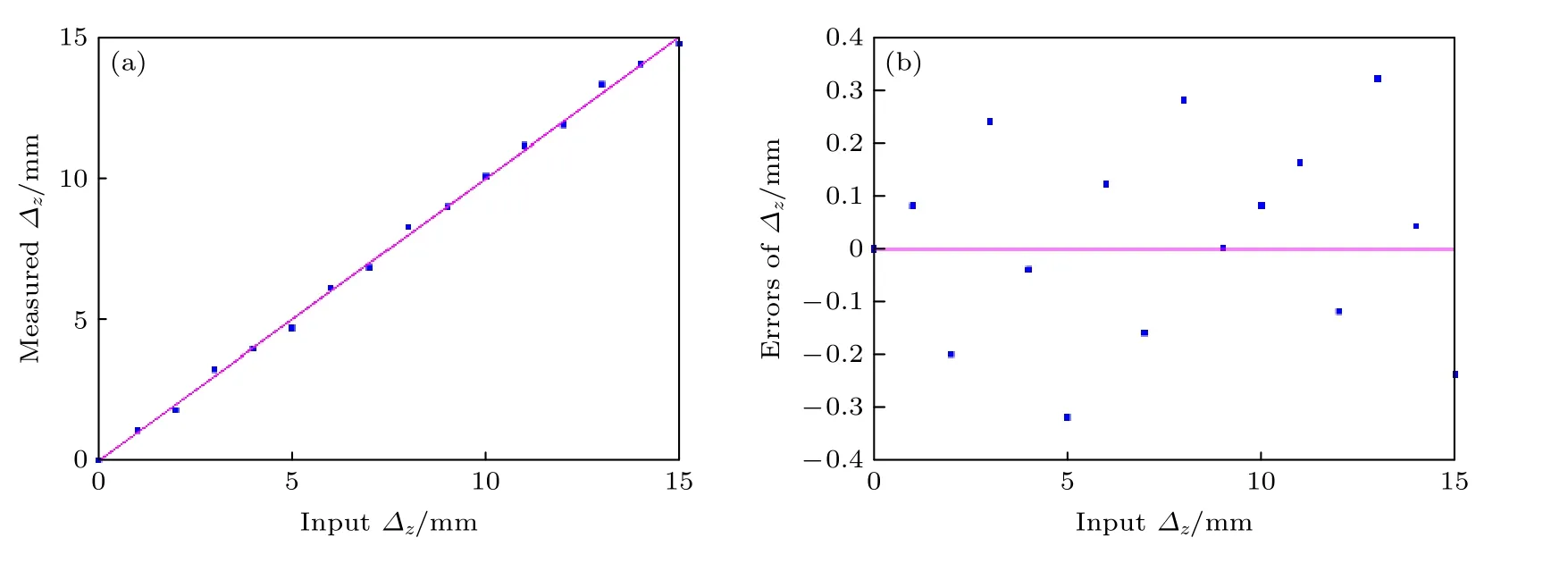
图9 当 Δ x = 0 mm、 Δ y = 0 mm 时轴向位移测量结果Fig.9.Measurement results of out-of-plane displacement when Δ x = 0 mm and Δ y = 0 mm.

图10 当 Δ y = 0.15 mm、 Δ z = 7.90 mm 时实验得到的莫尔条纹图Fig.10.Moiré patterns captured by experiment when Δ y = 0.15 mm and Δ z = 7.90 mm.

z轴测量误差大于x轴和y轴.这是因为莫尔条纹的变化对x轴和y轴位移更敏感.如图6 和图8所示, 当z轴位移量在1 个Talbot 距离(15.8 mm)内变化时, 由相移引起的莫尔条纹变化十几个像素.这导致该测量方法对z轴位移测量的灵敏度较低, 误差较大.通过选择合适的光栅和提高图像采集设备的分辨率, 可以提高测量精度.

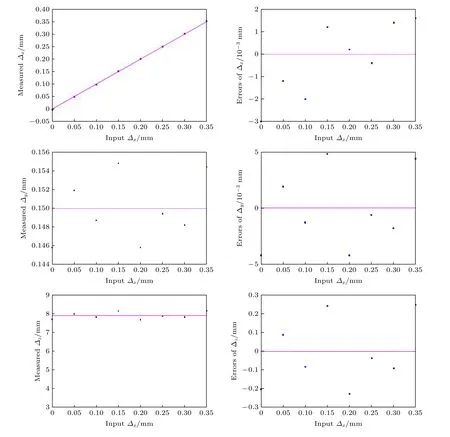
图11 当 Δ y = 0.15 mm、 Δ z = 7.90 mm 时三维位移测量结果Fig.11.Measurement results of 3D displacements when Δ y = 0.15 mm and Δ z = 7.90 mm.

表1 实验测量结果及误差Table 1.Measurement results and errors of experiment.

5 结 论

本文研究了基于双圆光栅径向剪切干涉仪的三维位移测量方法, 通过空间滤波技术同时得到+1 和–1 级莫尔条纹图像, 并提出了相应的位移量提取算法.二维平面内位移可分别用+1 或–1 级莫尔条纹进行测量, 轴向位移用+1 和–1 级莫尔条纹之间的相移来测量.该方法采用同轴成像的径向剪切干涉仪, 与需要采集不同视角莫尔条纹的三维位移测量方法相比[20], 可利用单个探测器拍摄到的一幅莫尔条纹图实现三维位移的瞬时测量, 并具有相同的测量精度.总而言之, 该方法具有装置简单、测量精度高、非接触、瞬时测量等特点, 可实现三维位移的同时测量.