有限脉冲响应滤波器在电力系统谐波鲁棒估计中的应用

陈 彪，方旭峰，陈识微

(1.国网杭州富阳供电公司，浙江 杭州 311400； 2.浙江容大电力设备制造有限公司，浙江 杭州 311000)

目前，由于电力电子设备的大量使用，电能质量已经成为电力系统操作中的重要问题。与电力系统相连的非线性负荷会导致谐波水平的增加，这些谐波会导致与电力系统运行相关的严重问题，如电压畸变、损耗增加、发热[1-2]。电力系统谐波是衡量电能质量的重要指标之一，因此有必要对电力系统谐波成分进行估计，以提供高质量的电能。在许多电力系统中的应用程序，快速傅里叶变换和离散傅里叶变换由于计算速度快且简单，被广泛用于估计电压或电流信号的谐波分量[3-4]，这两种方法都能准确地估计静止无噪声信号的谐波分量。然而，快速傅里叶变换和离散傅里叶变换在其推导过程中都没有考虑噪声干扰因素，仅适用于平稳信号。对于非平稳且有噪声的信号，这两种方法会导致精度下降，性能也较差[5]。

为了抑制噪声和处理时变谐波，相关专家学者提出了基于卡尔曼滤波的方法，用状态空间表示噪声信号[6]。但是，这些方法本质上需要系统的先验信息和信号，而这些信息很难获取。尤其是卡尔曼滤波器的最佳性取决于过程和测量噪声协方差矩阵的准确性。过程和测量噪声协方差矩阵的较小值会产生不可靠的估计，而较大的值可能会导致估计结果存在差异。因此，基于卡尔曼滤波的方法可能会有较差的性能。为了解决这些问题，研究人员提出了基于修正卡尔曼滤波的谐波估计技术。王少英[7]认为，估计结果更多地取决于过程和测量噪声协方差矩阵的比值，而不是它们各自的值。王艳等[8]提出了利用2个过程噪声协方差矩阵进行动态谐波跟踪估计的方法。崔永林等[9]提出了一种自调整模型误差协方差的方法来跟踪谐波波动。然而，由于卡尔曼滤波器是无限脉冲响应(Infinite Impulse Response，IIR)结构滤波器，它利用了从初始时间到当前时间的所有信息[10]，并具有内部状态，因此在状态中可能会积累不确定性。

本文提出了利用最佳FIR滤波器对电力系统谐波进行鲁棒估计的方法，将带有噪声的电流或电压信号表示为状态空间模型，将信号的谐波分量表示为状态变量，然后采用最佳FIR滤波器来估计谐波分量的大小。由于在所提出的方法中使用的最佳FIR滤波器是由有限数量的过去测量值组成的线性组合，因此从有界输入和有界输出(BIBO)稳定性的角度，可以保证所提出方法的稳定性。与基于卡尔曼滤波的方法相比，该方法对临时不确定性和数值误差的估计更加稳健，以期为电力系统谐波估计提供更可靠的解决方案。

1 方法论

如果卡尔曼滤波器的误差动态在一定程度上是稳定的，则小的误差可能是发散问题的原因。因此，基于卡尔曼滤波方法的估计谐波对于具有建模误差或数值误差的系统可能会出现偏差。为了克服基于卡尔曼滤波的谐波估计方法的缺点，需要对电力系统谐波进行鲁棒估计。在信号处理领域，具有有限脉冲响应(Finite Impulse Response，FIR)结构的滚动时域或移动时域估计器被提出作为IIR结构估计器(如卡尔曼滤波器)的替代方案。由于FIR结构的滤波器使用最新的有限信息[11]，因此与IIR结构的滤波器相比，可以保证有界输入/有界输出(BIBO)的稳定性，并具有更高的鲁棒性和更快的响应速度。此外，FIR估计器对过程噪声的敏感性低于IIR估计器[12]，可以用FIR滤波器代替卡尔曼滤波器对电力系统谐波进行鲁棒估计。

在电力调节系统中，包含谐波分量的电流或电压信号可以用测量噪声表示为式(1)：

(1)

式中，m为谐波阶数；am，t和θm，t分别为第m个谐波分量在时间t处的大小和相位角；ω为电力系统的基本频率；vt为测量噪声，它是一个协方差为RS的零均值白高斯随机过程。

设采样时间间隔为Δt=tk+1-tk，时间指数k为第k个采样时间(tk=Δtk)，则在k时刻的信号可以表示为式(2)：

(2)

式(2)可以表示线性时不变状态空间模型。

假设第m个谐波分量的方差Δam，k(m=1，…，M)服从随机游走运动，则第m个谐波分量在k+1时刻的大小可以表示为式(3)：

Δam，k+1=am，k+Δam，k

(3)

设状态变量xk为式(4)：

(4)

那么k+1时刻的信号可以表示为式(5)：

(5)

结合式(5)，式(2)的时不变状态空间模型可以表示为式(6)、式(7)：

(6)

yk=Hxk+vk

(7)

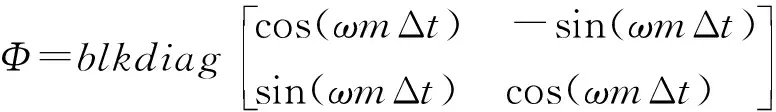
(8)

H=[1 0 … 1 0]

(9)

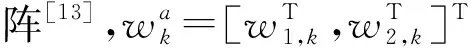
为了设计最佳FIR滤波器，考虑以下状态空间模型：

xk+1=Axk+Gwk

(10)

yk=Cxk+vk

(11)

式中，xk为状态向量；yk为测量值；wk和vk分别为过程噪声和测量噪声。同时，wk和vk分别为具有协方差Q和R的高斯白随机噪声。

最佳FIR滤波器可以设计为时域[k-N，k-1]有限测量的线性函数：

(12)

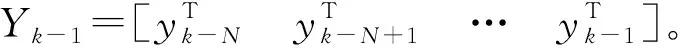
2 性能评估

通过仿真来评估方法的性能，考虑以下电压信号谐波：

y(t)=acos(ωt+60)+0.1cos(3ωt+15)+0.095cos(5ωt-10)+0.035cos(7ωt+40)+0.014cos(9ωt+30)+0.01cos(11ωt+50)+0.02cos(13ωt+70)+v(t)

(13)

标称系统频率f=60 Hz，数据采集单元的采样频率为1.62 kHz(每个周期27个采样)。

为了说明基于最佳FIR滤波器方法的性能，针对状态空间模型(6)和(7)分别实现了最佳FIR滤波器、时变(Time Varying，TV)卡尔曼滤波器和自适应卡尔曼滤波器，并对仿真结果进行了比较。

2.1 时不变谐波分量

针对含有时不变谐波分量的信号，将基于最佳FIR滤波器方法与时变卡尔曼滤波器进行了比较，验证该方法的估计性能。在该仿真场景中，式(13)中的设为1.0，比设为0.25，测量噪声的协方差为0.05。测试信号的波形如图1所示。

图1 带时不变谐波分量的测试信号波形Fig.1 Test signal waveform with time invariant harmonic component

模拟中使用的时变卡尔曼滤波器设计如下。

(1)时间更新。

①预测未来状态：

(14)

②预测未来误差协方差：

Pk|k-1=APk-1|k-1AT+Q

(15)

(2)测量更新。

①计算滤波器增益：

Kk=Pk|k-1CT(CPk|k-1CT+R)-1

(16)

②通过测量更新估算值：

(17)

③更新误差协方差：

Pk|k=(I-KkC)Pk|k-1

(18)

仿真参数设置如下：选取最佳FIR滤波器的时域尺寸为14，TV 卡尔曼滤波器设计的初始状态和初始估计误差方差分别设置为x0=[1 1 … 1]T和P0=10×I。

图2、图3和表1分别比较了2种方法对各谐波分量的估计幅度及其均方根估计误差。从这些结果可以看出，基于最佳FIR滤波器方法和基于TV 卡尔曼滤波的方法均提供了可靠的估计结果。由于本文方法中使用的最佳FIR滤波器是一个时不变滤波器，因此该方法将比基于TV卡尔曼滤波器的方法具有更好的计算效率。为了比较计算效率，比较了2种算法每次迭代的平均计算时间：最佳FIR滤波器、TV卡尔曼滤波器计算时间分别为0.971、1.517 μs。该方法的计算时间比基于TV 卡尔曼滤波器方法的计算时间少23%左右。

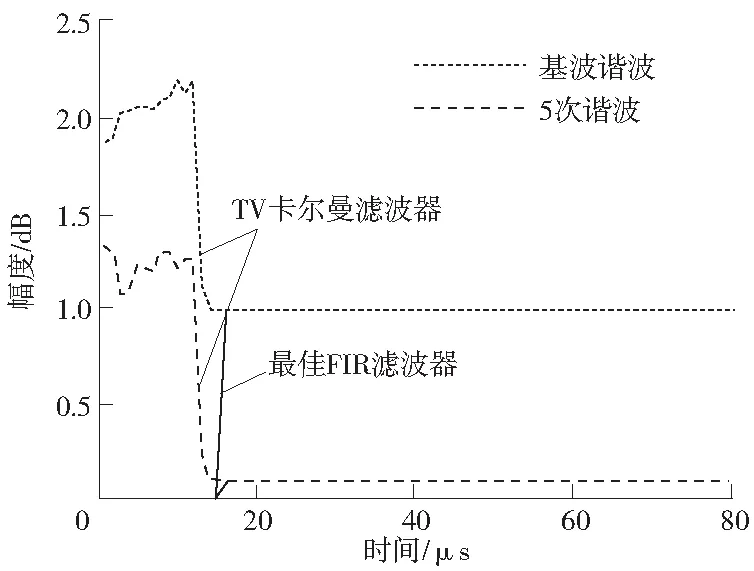
图2 基波谐波分量和5次谐波分量的估计值比较Fig.2 Comparison of estimated values of fundamental harmonic component and 5th harmonic component

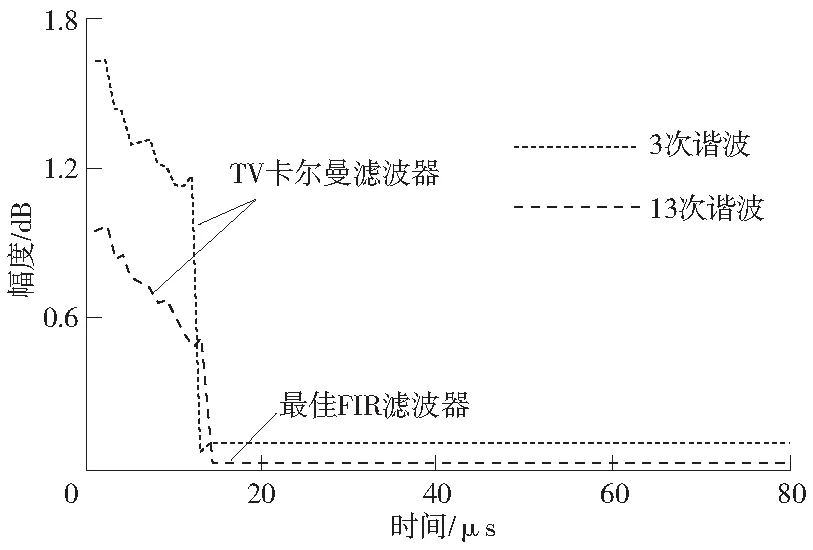
图3 3次和13次谐波分量的估计幅度比较Fig.3 Comparison of estimated amplitudes of 3rd and 13th harmonic components

表1 均方根估计误差Tab.1 Root mean square estimation error 10-3

2.2 时变谐波分量

为了验证基于最佳FIR滤波器方法的鲁棒性和跟踪性能，考虑了具有时变谐波分量的信号。对于这种情况，将式(13)中的设置为：

(19)

带时变谐波分量的测试信号如图4所示。

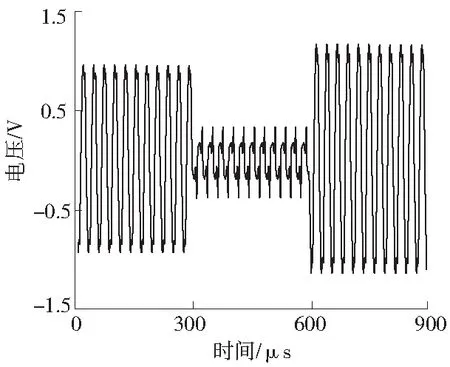
图4 带时变谐波分量的测试信号波形Fig.4 Test signal waveform with time varying harmonic component

为了验证FIR结构滤波器的使用效率，将本文方法与基于TV 卡尔曼滤波器的方法对具有时变谐波分量的测试信号进行了比较。

表2和图5分别给出了不同Q/R比(R=0.05，为常数)下基波分量的估计量及其均方根估计误差。从这些结果中可以看出，所提方法的估计没有明显的变化，而TV卡尔曼滤波器的估计不能收敛到实际幅度[16]。这些结果验证了基于FIR结构滤波器的方法对协方差矩阵的敏感性较低。因此，可以说该方法比基于卡尔曼滤波器的方法具有更强的鲁棒性。在图5中，2种方法的振荡行为是由于测量噪声vk和不准确的过程噪声协方差矩阵引起的。此外，将基于FIR结构滤波器方法与基于自适应卡尔曼滤波器的方法进行了比较，以验证其鲁棒性和收敛能力。自适应卡尔曼滤波器与TV卡尔曼滤波器具有相同的结构，不同的是，每次迭代都对过程和测量协方差矩阵和进行相应调整[17]。

表2 不同Q/R时的均方根估计误差比较Tab.2 Comparison of root mean square estimation error under different Q/R

设计自适应卡尔曼滤波器，初始状态和初始估计误差方差的设置与TV 卡尔曼滤波器参数相同。本文所提出的方法和基于自适应卡尔曼滤波器方法的均方根估计误差见表3。结果表明，所提出方法的估计误差小于基于自适应卡尔曼滤波器方法的估计误差。

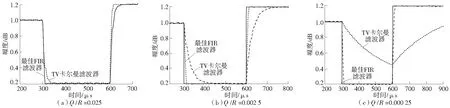
图5 基波分量的估计幅度比较Fig.5 Comparison of estimated amplitudes of fundamental components

表3 均方根估计误差比较Tab.3 Comparison of root mean square estimation error 10-3

基于FIR结构滤波器方法和基于自适应卡尔曼滤波器方法的谐波分量估计幅度如图6、图7所示。

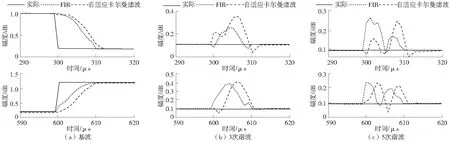
图6 基波、3次谐波和5次谐波分量的实际和估计幅度Fig.6 Actual and estimated amplitudes of fundamental，3rd and 5th harmonic components

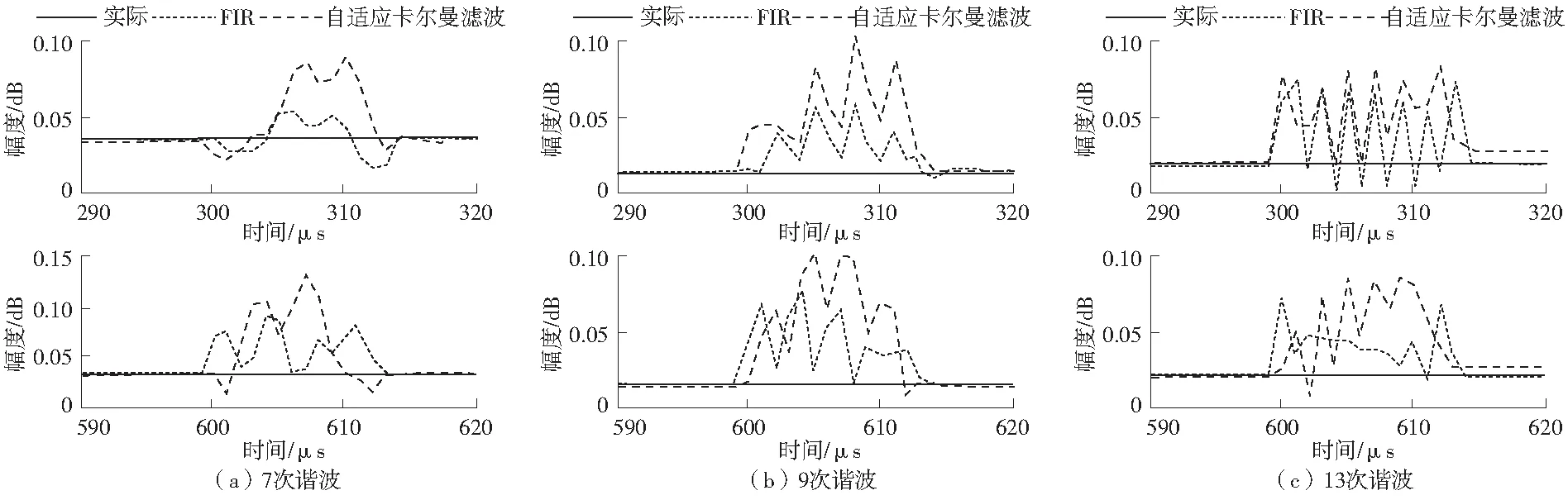
图7 7次、9次、13次谐波分量的实际和估计幅度Fig.7 Actual and estimated amplitudes of 7th，9th and 13th harmonic components

从图6、图7中可以看出，与基于自适应卡尔曼滤波器的方法相比，基于FIR结构滤波器方法的估计能更快地收敛到每个谐波分量的真实幅度。另外，由于自适应卡尔曼滤波每次迭代都需要计算和。因此，本文所提出方法的计算时间少于基于自适应卡尔曼滤波器方法的计算时间。最佳FIR滤波器、TV卡尔曼滤波器每次迭代的平均计算时间分别为0.972、3.579 μs，基于FIR结构滤波器方法比基于自适应卡尔曼滤波器方法的计算时间少72.84%。

3 结语

提出了一种鲁棒估计方法来估计电力系统谐波分量的幅值。为了设计鲁棒的估计器，将最佳FIR滤波器应用于有噪声电流或电压信号的状态空间表示。由于该方法所使用的最佳FIR滤波器由有限个过去测量值的线性组合所组成，因此该方法可以避免基于卡尔曼滤波器方法中可能出现的散度问题。与基于卡尔曼滤波方法相比，该方法因使用了FIR结构的滤波器来估计谐波分量，可以提供更稳健的不确定性和数值误差估计。由于最佳FIR滤波器不使用任何初始状态的先验信息。因此，提出的谐波估计方法可以避免未知初始状态引起的误差。仿真结果表明，与基于卡尔曼滤波的方法相比，该方法对过程噪声的敏感性较低。