氢气-乙醇预混燃气层流燃烧火焰结构不稳定性分析

2021-05-07王筱蓉陈家兴

沈阳大学学报(自然科学版) 2021年2期

王筱蓉, 严俊, 陈家兴, 李童

(江苏科技大学机械工程学院, 江苏镇江 212003)

随着日益严格的环境保护政策和国家可持续发展战略的出台,可再生、低排放能源发展已成为当前能源研究的主题和重点[1].氢气燃烧的化学产物只有水,没有二氧化碳、硫化物等污染物[2],是世界上最清洁的能源.目前氢气制备有生物制氢和水解制氢等多种方法,这些方法可以控制氢气生产的成本[3],但氢气的爆炸极限较低,燃烧过程不稳定,从而限制了其作为燃料的发展.因此,为确保氢气在燃烧过程中的稳定性,常用的解决方案是添加其他低热值能源降低氢气的爆炸极限[4].

在标准层流燃烧火焰中,火焰表面是稳定的,但具有高比例氢气的预混燃料的层流燃烧过程会产生不稳定变化,这是火焰从层流燃烧转变为湍流燃烧的重要过程[5].对这一过程中不稳定火焰的形态和产生因素的分析是预测未来火焰形态发展的前提,也为提高燃烧效率和稳定性提供了依据.1986年,Yu等[6]在甲烷、乙烷等低热值碳氢燃气中添加少量氢气,利用对冲滞止火焰法对预混燃气的层流燃烧特性进行研究,测量了一部分预混燃气的层流燃烧速度,结果表明,氢气的加入促进了低热值燃料的燃烧.张勇等[7]利用定容燃烧弹对甲烷-氢气预混燃气的层流燃烧速度进行测定,并研究了不同点火能量对燃气火焰传播的影响,同时通过测定不同预混比例燃气的马克斯坦长度,分析了氢气对火焰稳定性的影响.Liu等[8]对甲烷-氢气预混燃气在层流燃烧过程中的燃烧损失进行了测定,结果表明,伴随当量比的增加和火焰厚度的减小,传热效率会有所降低,进而使火焰热损失增大.Tang等[9]对丙烷-氢气预混燃气的燃烧过程进行了实验,从氢体积分数小于60%开始,燃料马克斯坦长度会随着当量比的减小而减少,表明火焰越不稳定,Lewis数会随着氢比例的提高而减小,燃烧过程中的扩散不稳定性逐渐增大.张欣等[10]对低热值气体掺混氢气火焰稳定性进行了研究,结果表明,火焰燃烧中会出现胞化火焰、局部熄灭和再燃3种形态,氢气体积分数的提高会使胞化火焰出现时间提前以及胞化火焰幅值提高,燃料燃烧进程中CO2浓度的提高会使火焰不稳定状态受到抑制.以上结果均表明,氢气的体积分数对于火焰稳定性有很大影响.

本实验通过利用少量乙醇与氢气预混燃气燃烧来降低燃料的热值.对充分混合后的预混燃气进行了层流燃烧实验,对层流燃烧过程火焰结构变化和参数变化进行了定性和定量测定,分析了影响氢气-乙醇预混燃气火焰不稳定性的因素.

1 实验设备

本次实验采用的是球形火焰法[11],实验设备示意图见图1.实验利用电极在恒定体积的燃烧弹中点燃混合气体,并通过高速相机拍摄球形火焰,以获取火焰膨胀的图像.实验设备由以下模块组成:定容燃烧弹、点火系统、数据采集系统以及气体供应与排放系统.定容燃烧弹内通过PID控制器控制弹体内壁上加热电阻进行加热,温度显示器显示弹体内部温度; 压力表实时监测弹体内的压强变化;压力传感器连接示波器用于记录实验过程中定容燃烧弹内部的压力变化;燃烧弹内中心位置有2根相对的电极用于点火;定容燃烧弹相对的两侧装有石英玻璃视窗,提供了实验数据采集时光路传输通道.同步触发器连接高速摄像机、点火控制器和示波器,由电脑同步触发开始信号.实验中使用的高速相机的帧率为10 000帧/S,分辨率为1024×1024.在实验中,由体积分数为90%的氢气和10%的乙醇组成的预混燃气在定容燃烧弹中进行混合后点火燃烧,对其在不同当量比(φ)条件下火焰不稳定进行分析.本实验的预混燃气以φH2=90%表示.

图1 设备示意图Fig.1 Schematic diagram of the experimental device

2 结果与讨论

2.1 层流燃烧特性分析

本实验通过控制预混燃气和空气的不同比例,即调节预混气体的当量比(φ),来测定不同反应过程中预混燃气的火焰变化.当预混燃气完全和空气反应时φ=1;当反应后燃料剩余,即为氧气的量不足时φ<1;当反应后氧气剩余,即为氧气富余时φ>1.高速摄像机拍摄到的火焰图像进行后期处理后,得到火焰图像的扩展参数,用以研究层流火焰的燃烧特性.由于火焰扩展过程中表现出不稳定行为,无法成为平滑的球形火焰,所以本实验提取拍摄到的各个时刻的火焰纹影图像中的球形火焰面积,通过面积等效得到平滑的球形火焰,计算各个时刻等效火焰的等效半径Rf,mm.通过等效半径Rf的变化率计算球形火焰传播速度Sb[12],

(1)

式中,t为点火后的时间,s;由于火焰在传播过程会受到拉伸作用,此时的火焰传播速度Sb又称为拉伸火焰传播速度,mm·s-1.

火焰拉伸率α定义为火焰表面积A内无限小的区域所对应的时间导数,s-1,由此可以推导出球形火焰拉伸变形的计算公式[13],

(2)

图2为φH2=90%时5种当量比下球形火焰等效半径随时间的变化. 当预混燃气处于贫燃状态时, 火焰等效半径的增长规律近似线性, 当量比增大时, 等效半径增大速度加快. 随着φ的增加,相邻当量比之间的火焰等效半径的间距逐渐减小, 即在稀薄燃烧状态下伴随当量比增加, 火焰扩展加速度减小.

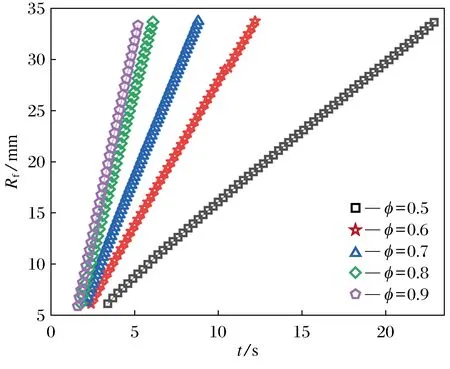
图2 5种当量比下球形火焰等效半径随时间的变化Fig.2 Variation of spherical flame radius with time under five equivalence ratios

图3为5种当量比下火焰拉伸率随等效半径的变化.图中曲线的变化规律相似,随着当量比的增加,火焰的拉伸率随之提高,当量比一定时,火焰的拉伸率随等效半径呈指数式下降,当火焰等效半径增加到一定范围,拉伸率的降低趋势逐渐平缓.由于火焰等效半径的扩大,火焰拉伸率降低,火焰的拉伸效应逐渐不能抑制火焰的突起,进而导致火焰裂纹的产生,直至胞化形成.图中φ=0.7和φ=0.8曲线之间间距较大,表明燃料燃烧过程中层流预混火焰的稳定性在φ为0.7～0.8的过程中变化较大.

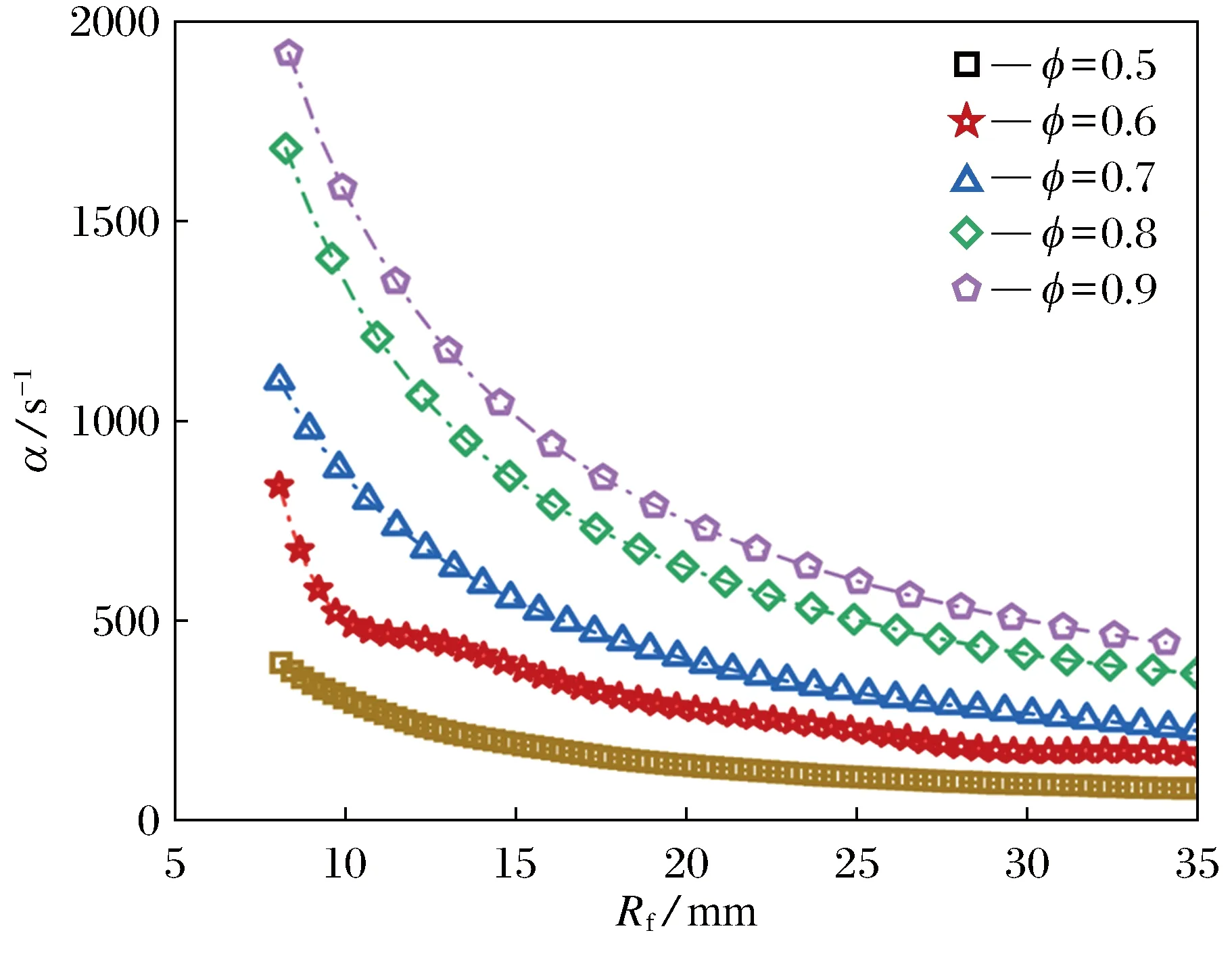
图3 5种当量比下火焰拉伸率随火焰等效半径的变化Fig.3 The variation of elongation with equivalent radius under five equivalent ratios

通过选取层流火焰稳定燃烧的区域,外推计算其拉伸火焰传播速度和拉伸率之间的变化[14].图4为燃料在5种当量比下的拉伸火焰传播速度随火焰拉伸率的变化.通过线性拟合的方式可以测定其马克斯坦长度(Lb)和无拉伸火焰传播速度(Sn),线性公式[15]为

Sb-Sn=Lbα.

(3)

式中,Lb用以表征拉伸火焰传播速度对拉伸率变化的敏感度[16],mm,是火焰传播过程中火焰稳定性进行量化分析的一个重要参数.利用线性外推法,曲线外推至拉伸率无限小时,对应的火焰传播速度即无拉伸火焰传播速度Sn,mm·s-1.

从图4中的曲线变化趋势可以看到,拉伸火焰传播速度随φ的增加而增大,但其与拉伸率的变化趋势随φ的增加逐渐平缓.

图4 5种当量比下拉伸火焰传播速度随拉伸率的变化Fig.4 Variation law of stretching flame propagation speed and stretch rate of premixed gas at five equivalence ratios

利用Lb的取值对火焰未来的发展状态进行分析预测.当Lb<0时,表示拉伸火焰传播速度随拉伸率增加而增大,球形火焰表面产生不稳定的突起,在火焰传播速度随半径逐步增大时,突起会逐渐严重,火焰趋于不稳定性状态[17].图5为马克斯坦长度随当量比的变化,从图中可以看到,φH2=90%的预混燃气在当量比范围为0.5～0.9的条件下,所有工况下的Lb<0,这意味着拉伸火焰传播速度会伴随拉伸率的增加而增大,尤其当火焰处于不稳定状态时,会使火焰前锋面上的突起随火焰传播速度的增加而加剧,火焰向胞化不稳定方向发展.

图5 马克斯坦长度随当量比的变化Fig.5 The change law of Markstein length with the increase of equivalence ratio

2.2 火焰不稳定状态分析

火焰的不稳定状态受到的影响因素包括:浮力不稳定、扩散不稳定以及流体动力学不稳定[18].其中浮力不稳定是由于球形火焰扩散过程中,已燃气体密度远远小于未燃气体密度,导致已燃气体无法克服重力,火焰的形貌呈现蘑菇状向上.本次实验未出现此类现象,所以实验中未作考虑.

图6为5种当量比下层流火焰扩展的不稳定火焰纹影图像.当火焰半径小于10 mm时,不同当量比的火焰形态变化不大,火焰形状基本能够保持规则的球形.火焰状态从15 mm开始变化,φ=0.5时,在火焰的两端出现凸起,并且火焰褶皱开始扩散;φ=0.6时,相同半径下的火焰中仅出现细小裂纹;φ=0.9时,火焰仅在恒压段的末端出现小裂纹.φ=0.9、Rf=15 mm时,火焰仅在膨胀中变化,并且火焰形态在后面时间里保持相似变化,随当量比的减小,火焰褶皱出现的火焰半径变小.5种当量比下火焰半径的不稳定性变化规律从理论上解释了火焰中的流体动力学和传热传质不稳定火焰出现的形貌变化[19].

当量比较低时,预混火焰产生的不稳定性主要是传质传热不稳定性,原因是层流火焰的扩展过程中,火焰前锋面两侧进行着化学反应,而在反应过程会发生传热和传质过程.传质传热的不平衡可能产生气体扩散不稳定,这种扩散不稳定性能够通过路易斯数(Le)进行判定[20].路易斯数是描述对流过程中传热传质状态的无量纲参数,能够通过热扩散系数(DT,m2·s-1)与不足反应物质量扩散系数(Dim,m2·s-1)的比值来计算,计算公式为

(4)

图6 5种当量比下不稳定火焰的纹影图像Fig.6 Schlieren images of unstable flames at 5 equivalence ratios

火焰扩散不稳定性机理示意图如图7所示,Le<1的状态代表了反应阶段的热扩散系数要小于质量扩散系数,其火焰前锋正向拉伸反应的热扩散引起的能量损失小于反应物的物质扩散带来的能量输送,从而使未燃区域的拉伸速度增加,火焰前锋面的拉伸行为越来越剧烈,相对于Le>1的状态,火焰不稳定加剧.

图7 火焰扩散不稳定性机理示意图Fig.7 Schematic diagram of diffusion instability mechanism

层流火焰不稳定变化还可以结合路易斯数的变化规律来解释[21].图8为燃料在温度为400 K时5种当量比下的路易斯数变化.当量比在0.5～0.9之间,燃料球形火焰在扩展过程中路易斯数的数值都小于1,这表明其在反应阶段的热扩散系数小于质量扩散系数.通过对反应机理的分析,可以得出热扩散率小于质量扩散率,减少了对燃烧区域拉伸的结论[22].拉伸变形严重使火焰更加不稳定,这种不稳定性将随当量比的减小而增加,这也同时解释了路易斯数小于0时的上述变化规律,火焰传播速度将随着路易斯数的减小而减小.当φ=0.7时,与数据拟合曲线相比,Le的数据点减少较多,这与前文拉伸速度的变化规律相似,也进一步证明了火焰的不稳定性是在φ在0.7～0.8之间产生改变的.

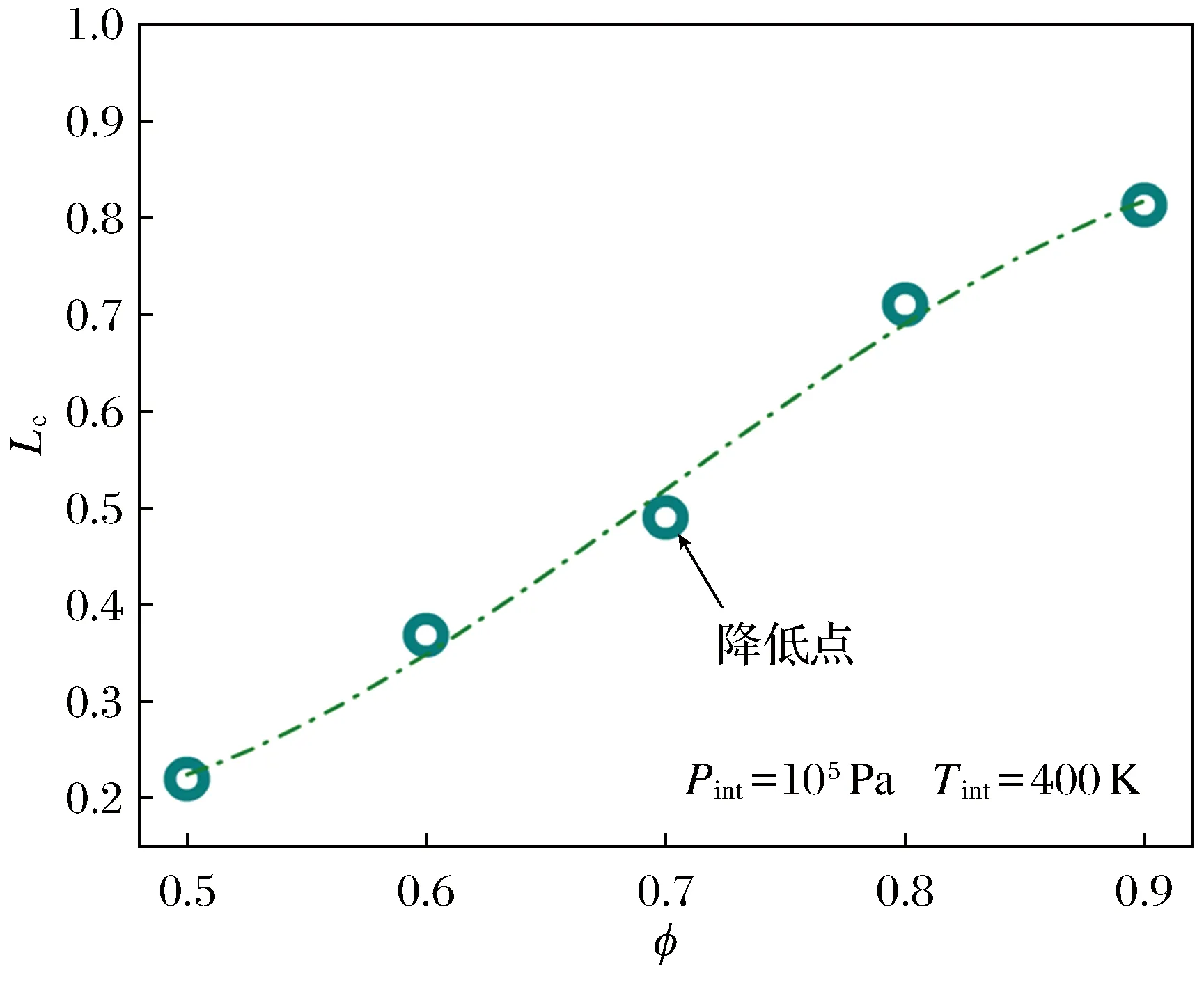
图8 路易斯数随当量比的变化Fig.8 The law of Lewis number changing with equivalence ratio

通过火焰纹影图像,可以观察到不稳定的层流火焰在火焰前沿具有不同形状和大小的突起和裂纹[23].由于火焰拉伸引起火焰前表面的褶皱和突起,不能直接获得火焰半径,因此采用面积的等效获得火焰半径.图9为等效半径为30 mm时,当量比为0.5和0.9的层状火焰实际半径与等效半径之间的波动.由于火焰的不稳定性,与等效火焰相比,实际火焰的前表面是波动的,因此对实际火焰半径R与等效火焰半径Rf随火焰角度变化进行比较,能够判定火焰不稳定性对火焰形貌的影响.将火焰等效半径和实际半径的间距标记为R0(R0=R-Rf,mm).从图中可以看到,在火焰等效半径30 mm处,火焰前锋的凸起更加明显,此条件下可以更清晰地呈现火焰结构的不稳定性变化.2种当量比的R0波动趋势是相似的,表明不同当量比的火焰出现不稳定变化是相似的;角度为0°,180°和360°时,R0的绝对值最大,表明两侧火焰锋的突起最为严重;当量比增大时R0趋于平缓,当φ=0.9时半径差基本在1 mm以内,表明随火焰当量比的增加,火焰结构趋于平缓.

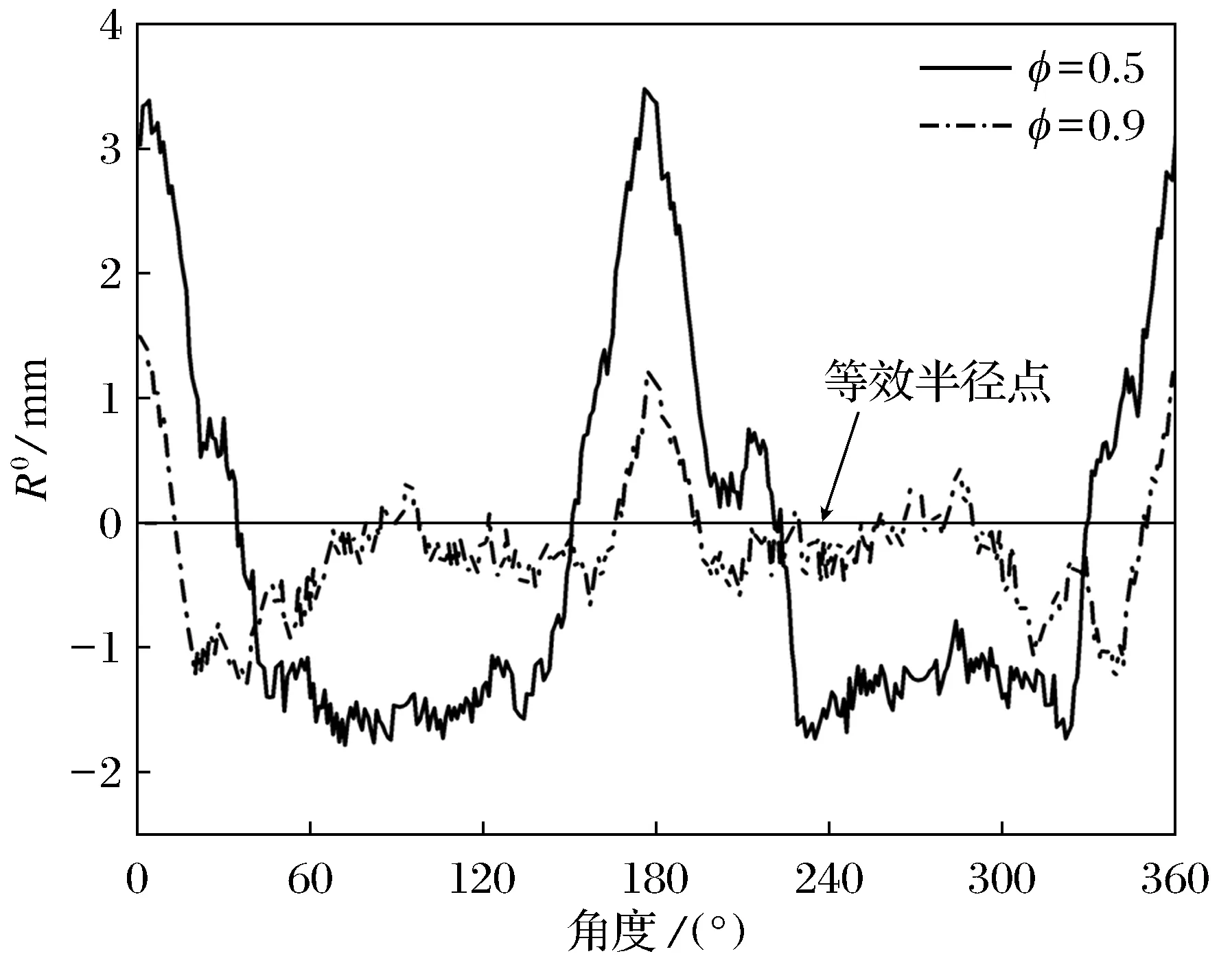
图9 等效半径30 mm时当量比为0.5和0.9的火焰实际半径与等效半径间距的波动Fig.9 Fluctuation between actual flame radius and equivalent flame radius under equivalent ratios of 0.5 and 0.9 at 30 mm equivalent radius

通过火焰厚度和热膨胀率也可以对这种球形火焰不稳定性进行因素探究[24].火焰厚度(δ,mm)定义为混合气体燃烧空间和未燃烧空间的距离,计算公式为

(5)

式中:Tb为燃烧过程中已燃气体温度,K;Tu为未燃气体温度,K;(dT/dR)max为球形火焰膨胀过程中温度变化的最大点,K·mm-1.

由于热力分布的不均匀性导致火焰发展过程中产生流体动力学不稳定状态,可以通过火焰前锋面的热膨胀系数变化来测定其影响大小,热膨胀系数σ定义为未燃气体和已燃气体之间的密度跳动变化,即表示为未燃气体密度和已燃气体密度之间的比值,其计算公式为

(6)

图10 火焰厚度与热膨胀系数随当量比的变化Fig.10 Variation law of flame thickness and thermal expansion coefficient with equivalence ratio

式中,ρu表示未燃气体密度,kg·m-3;ρb表示已燃气体密度,kg·m-3.火焰前锋面上的密度跳动引起火焰前锋面产生了胞化不稳定性,胞化前锋面热膨胀系数高时火焰容易产生不稳定.火焰厚度与热膨胀系数随当量比的变化如图10所示,从图中可以看到,燃料在不同当量比下进行的燃烧过程中,燃料的火焰厚度会随当量比的增加而变薄,整体趋势和火焰热膨胀率相反.火焰厚度的降低会提高火焰前锋面抵抗变形的能力,当量比的增加会减少火焰褶皱的产生,提高火焰的稳定性,因此火焰厚度是造成火焰不稳定的重要因素之一.