基于虚拟阻抗的低压微电网功率均分控制策略

（湖南工业大学 交通工程学院，湖南 株洲 412007）

1 研究背景

随着能源危机的日益加剧，清洁能源的需求大幅度提高，由多个分布式电源（distributed generation，DG）组成的低压微电网成为新能源高效利用的主要方式[1]。因此，低压微电网逆变器并联运行的控制方式逐渐成为众多学者的研究焦点。

微电网的独立运行使得DG 系统能够在各种类型电网故障时向负荷提供连续的电能。在实际多逆变器并联运行时，也存在诸多技术上的难题，例如功率的解耦控制，功率的精确分配和环流抑制问题[2]。因此，如何实现DG 间的功率均分，成为微电网孤岛运行时的首要难题。

在微电网的控制策略上，主要有集中控制、分布式控制和下垂控制等[3]。由于微电网中DG 单元分布广泛、种类较多，难以实现实时高速通信，而下垂控制的方法刚好避免了通信线路的使用，因此该方法得到了广泛应用[4]。但在低压微电网系统中，线路的电抗X远小于电阻R，这就使得低压微电网系统中的功率无法实现解耦，功率难以均分，针对这一问题，众多学者做了一系列的研究。

文献[5]采用虚拟阻抗和通信线路相结合的控制方式进行了优化控制，通过通信线路实时检测线路电压进行反馈，实现自适应调节虚拟阻抗进行电压补偿，不足之处在于通信线路的使用增加了线路的复杂程度和实际线路的成本，难以实现高速反馈。文献[6]在下垂控制环中添加功率影响项以改善电压降落问题，但该方法是将实际输出的无功功率值作为影响项，而忽略“虚拟阻抗”上的无功消耗，因此容易造成电压补偿不足。文献[7]将“虚拟阻抗”设计成负值，通过反馈控制使得线路中阻性部分得以抵消，保证了线路阻抗呈感性的假设，使得无功功率达到均分，不足之处在于“虚拟负阻抗”的值较难确定，若加入“虚拟阻抗”的抗性较大，会使得电压降落严重，甚至导致微电网运行失稳。文献[8]将实际的功率转换成虚拟功率，对传统下垂控制进行了改进，然而实际输出功率仍是耦合的，且控制算法较为复杂，难以推广应用。

为了解决传统下垂控制方法因线路阻抗不匹配引起的无功功率不能均分、环流过大的问题，本研究把改进下垂控制的虚拟阻抗法用于孤岛微电网系统。通过计算线路阻抗产生的压降来补偿电压的跌落，从而减小了功率的损耗，避免了互连线和通信设备的使用，保持了下垂控制的优势，同时解决了功率不能均分的问题。

2 直流微电网下垂控制策略

2.1 逆变器并联系统

微电网中的能源形势有多种，例如风力发电、光伏发电、燃料电池、储能装置等[9]。图1是微电网结构图，每个DG 单元包括能源输入、逆变器和滤波器，通过线路连接与配电网之间使用静态开关相互连通。能量监控与管理装置通过公共耦合点（point of common coupling，PCC）实时监控微电网的运行状态，保证微电网的稳定运行[10]。

图1 微电网结构Fig.1 Schematic illustration of the microgird

为简化分析多台逆变器并联的功率特性，本研究采用两台逆变器并联组成系统模型，如图2所示。

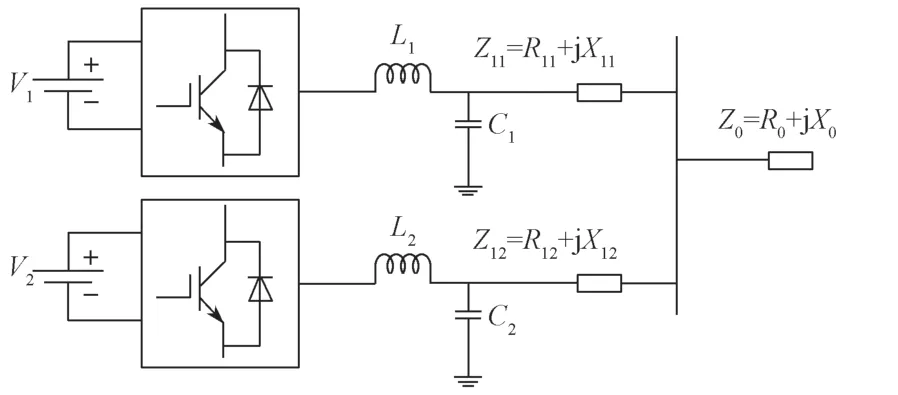
图2 逆变器并联系统模型Fig.2 Inverter parallel system model

图2中每个DG 单元通过馈线连接至母线。逆变器输出的电能通过LC 滤波器进行高频滤波处理，再由线路连接至母线。Zl1、Zl2为逆变器连接至母线的线路阻抗。Z0表示并联系统所带负载值。

2.2 传统下垂控制

为便于功率特性和环流的分析，将图2的两台逆变器并联系统模型简化，得出等效电路，如图3所示。

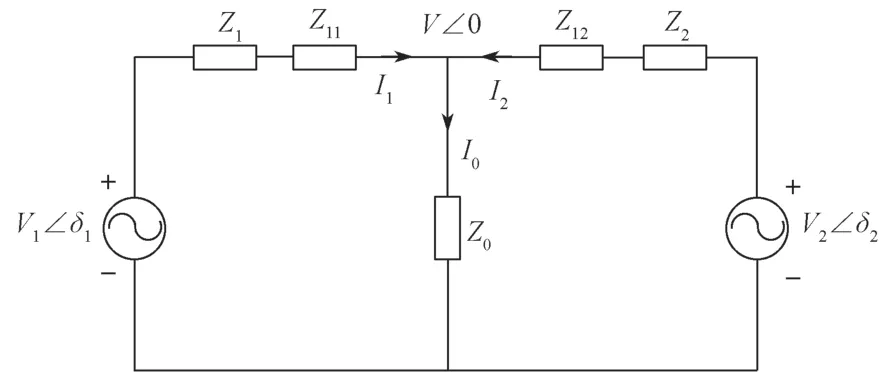
图3 逆变器并联系统等效电路Fig.3 Equivalent circuit of the inverter parallel system

设Vi为第i台逆变器的输出电压幅值，δi为第i台的功角，i=1,2,…,n；V为母线的电压幅值，I0为流过负载的电流，Ii为第i台逆变器的输出电流。则第i台逆变器输出的有功功率Pi和无功功率Qi的计算式分别如下：

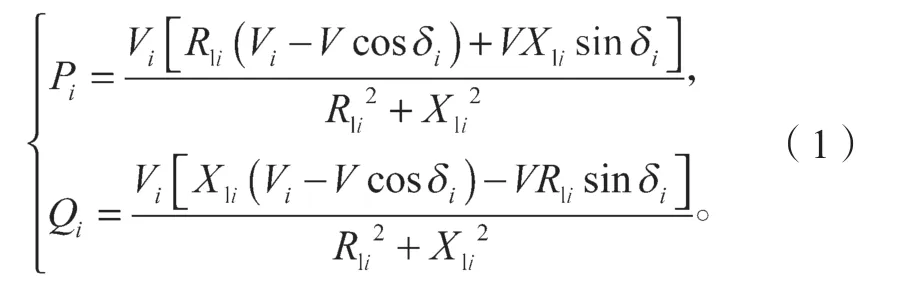
式中：δi为功角；Rli、Xli分别为线路的电阻和电抗。

在低压电网中，各个DG 单元通过线路连接到微电网母线。在线路阻抗R＜＜X时，可以将R忽略不计，则功率角δ很小，近似认为sinδ≈δ，cosδ≈1，将其代入式（1）可得：

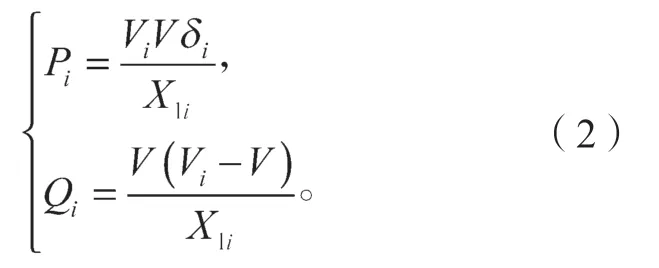
由式（2）可知，当线路呈感性时，在输出的视在功率中，有功功率的差异由功角决定，即功角越大，提供的有功功率越多；输出的无功功率由电压幅值决定，即电压幅值越大，输出的无功功率越大。

根据文献的分析，逆变器输出阻抗决定了下垂控制方程的选取。对于并联系统，当逆变器输出阻抗呈感性时，可以采用P-f、Q-V的解耦控制方法。对式（2）引入下垂系数，得到传统下垂控制方程：

式（3）中：mi、ni分别为第i台逆变器的P-f、Q-V控制的系数；fi、Pi分别为第i台逆变器输出频率和有功功率；Vi和Qi分别为第i台逆变器输出电压和无功功率；fi*、Pi*、Vi*、Qi*分别为第i台逆变器的频率、有功功率、电压、无功功率的给定值。

当线路阻抗呈感性时，两台逆变器的无功功率与线路阻抗有关，而有功功率关系不大。所以当并联逆变器的线路阻抗出现明显差异，下垂系数和容量相同的逆变器并联时，采用传统的下垂控制策略会出现明显的无功功率分配不均，而有功功率变化不大。相反，若线路阻抗呈阻性时，有功功率会分配不均，无功功率无明显差异。

2.3 逆变器环流分析

由图3所得示等效电路，可以求出两台逆变器的输出电流，为

根据环流的定义求得逆变器并联系统的环流为

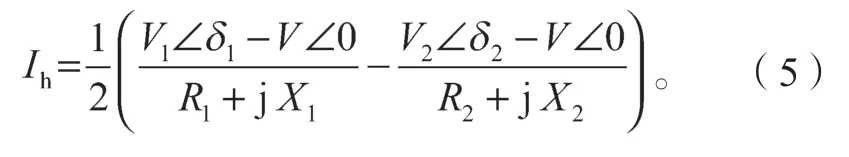
根据逆变器的输出电流容易求得系统为负载提供的复功率为

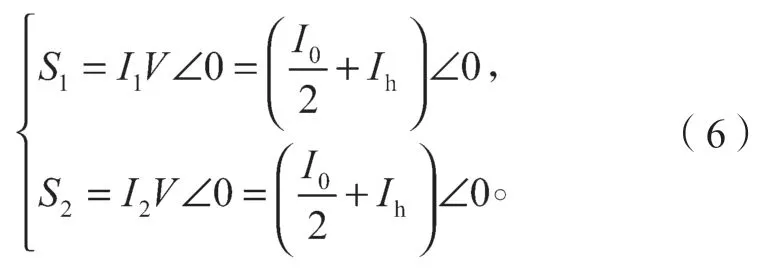
当线路阻抗不一致时，由于环流的存在，系统的无功功率输出不能精确分配。这样，不仅增加了能量的损耗，且严重时可能对逆变器造成损坏。根据式（5）容易看出，缩小两台逆变器输出电压差值，或者增加线路感抗均能减小系统的环流。

3 改进下垂控制策略

3.1 虚拟阻抗法

下垂控制法的使用条件是等效线路阻抗呈感性，而低压微电网的线路阻抗呈阻性，所以下垂法将无法较佳地实现功率解耦。在逆变器输出端增加虚拟阻抗回路，可使逆变器输出阻抗趋于纯感性[11]。图4为引入虚拟阻抗后的闭环控制框图。

图4 引入虚拟阻抗后的闭环控制框图Fig.4 Closed-loop control block diagram after the introduction of the virtual impedance

在引入虚拟阻抗后，输入电压电流双闭环中的电压就变成了下垂控制解耦后生成的参考电压值Vref和虚拟阻抗反馈的电压值的差。

记虚拟阻抗值为Zv，得到电压环的输入电压为

根据图4，可以求出此时逆变器的电压环传递函数为

式中：G(s)为双闭环控制下电压环传递函数；Vo、Io分别为逆变器的输出电压和电流；Zo(s)为逆变器到负载的阻抗传递函数。

分析式（8）可以得知，如果使得加入的虚拟阻抗的电感值足够大，能够忽略掉逆变器到负载的电阻值的时候，就可以保证线路阻抗呈感性。但是从式（7）可以看出，加入虚拟阻抗使线路呈感性的同时，也会导致电路电压的降落，增加的虚拟阻抗值越大，电压降落越明显。因此在保证线路阻抗呈感性的情况下，虚拟阻抗值应尽可能小。

3.2 改进的下垂控制策略

通过3.1 的分析可以知道，为了保证下垂控制法在低压微电网中能够很好地解耦，需要加入虚拟阻抗来保证线路阻抗呈感性。但是保证线路阻抗呈感性和电压降落是一对固有矛盾，即使虚拟阻抗值选取合适，也难免造成电压的降落，这样就会造成能源的损失。在加入了虚拟阻抗使功率可以解耦后，因线路阻抗不匹配所导致的无功功率输出不均分的问题仍然没有得到解决。为解决上述问题，本研究在基于虚拟阻抗改进的下垂控制法的基础上进行改进。

由于P-f控制方法是对功角进行调整，故存在积分环节，这样逆变器之间的功角就会相差很小，所输出的有功功率就能精确均分。因此，仅对Q-V的控制回路进行改进，修正由于线路电压不同而引起的无功功率不能均分。

在使得下垂控制能够解耦后，针对线路阻抗不匹配的问题，引入系统PCC 节点的电压进行补偿，减小线路电压的差异，从而抑制无功环流。为了有效利用下垂控制没有通讯互联线的优势，通过线路损耗公式求得ΔV，因其纵分量很小，通常忽略不计，所以采用横分量表示线路压降，其压降公式和改进后Q-V环公式如下：

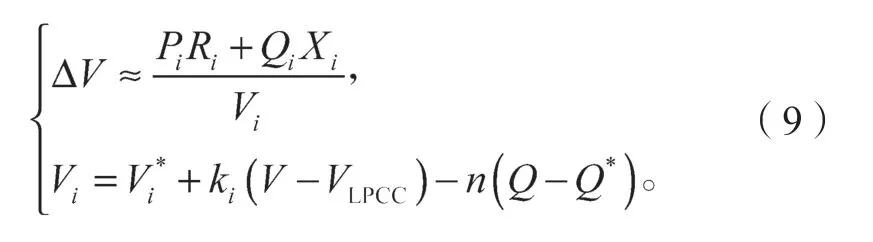
式中：ΔV为线路的压降；Ri、Xi分别为第i台逆变器的线路电阻和电抗值；ki为电压补偿系数；Vi*为第i台逆变器输出无功等于0 时对应的电压幅值；V为线路端电压；VLPCC为PCC 节点的电压，可通过压降损耗公式VLPCC=Vi-ΔV求得。

当系统处于稳态时，认为参考给定电压和反馈值之间不存在静态误差，可以表示为

图5为基于虚拟阻抗改进的下垂控制框图，P-f控制环和传统P-f一样，P和P*取差值后，经过下垂系数m得到Δf，Δf和f*取差值后经过I控制器得到输出频率。Q-V加入了电压补偿项，通过Vi和VLPCC求偏差后，经过补偿系数ki得到补偿电压，其再和额定电压Vi*叠加，进行电压补偿，最后与逆变器输出的无功功率和额定功率的误差经过下垂系数n得到的电压差求偏差，得到输出电压Vref。

图5 基于虚拟阻抗改进的下垂控制框图Fig.5 Improved droop control block diagram based on virtual impedance

若并联逆变器线路阻抗相同，取补偿系数ki=0，即得传统下垂控制方程；当并联系统线路阻抗不同时，取合适的ki可以进行电压补偿，不仅可以实现无功功率的精确分配，还可以减小电能的损耗，有效解决了传统下垂控制的局限性。

4 仿真验证与分析

本研究搭建了逆变器并联系统的仿真模型。采用两台逆变器并联，均使用直流电源提供电能。系统电压幅值设为310 V，仿真时间设为1 s，且在0.5 s 时增加公共负载。

为了验证本研究所提出的改进控制策略的可行性和正确性，把传统下垂控制策略与改进下垂控制策略进行仿真对比，分析线路阻抗不匹配的情况下改进下垂控制的特性。仿真模型参数及取值如表1所示。

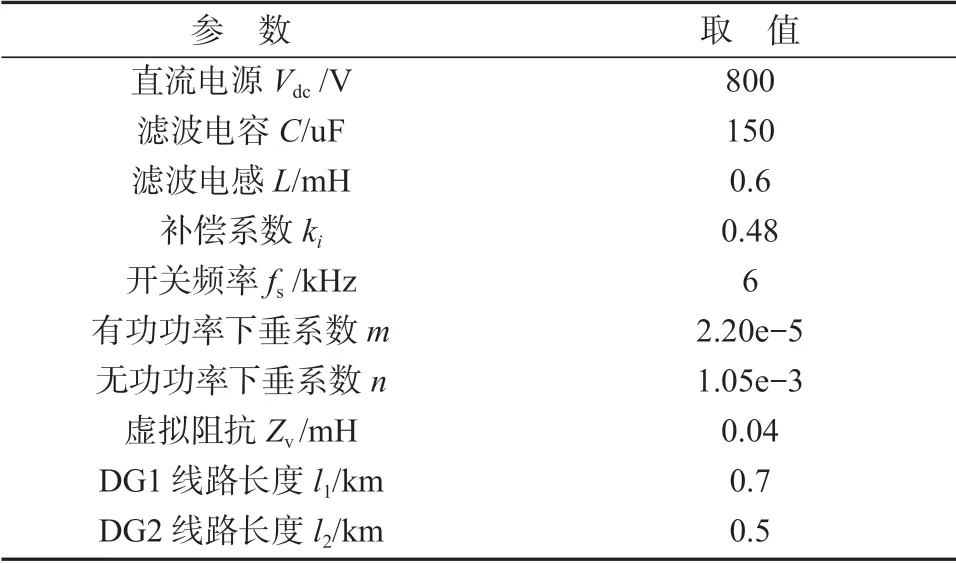
表1 仿真模型参数及取值Table 1 Parameters and values of simulation model

4.1 传统下垂控制策略仿真分析

传统下垂控制策略采用了两台相同容量的DG 并联运行，仿真结果如图6所示。

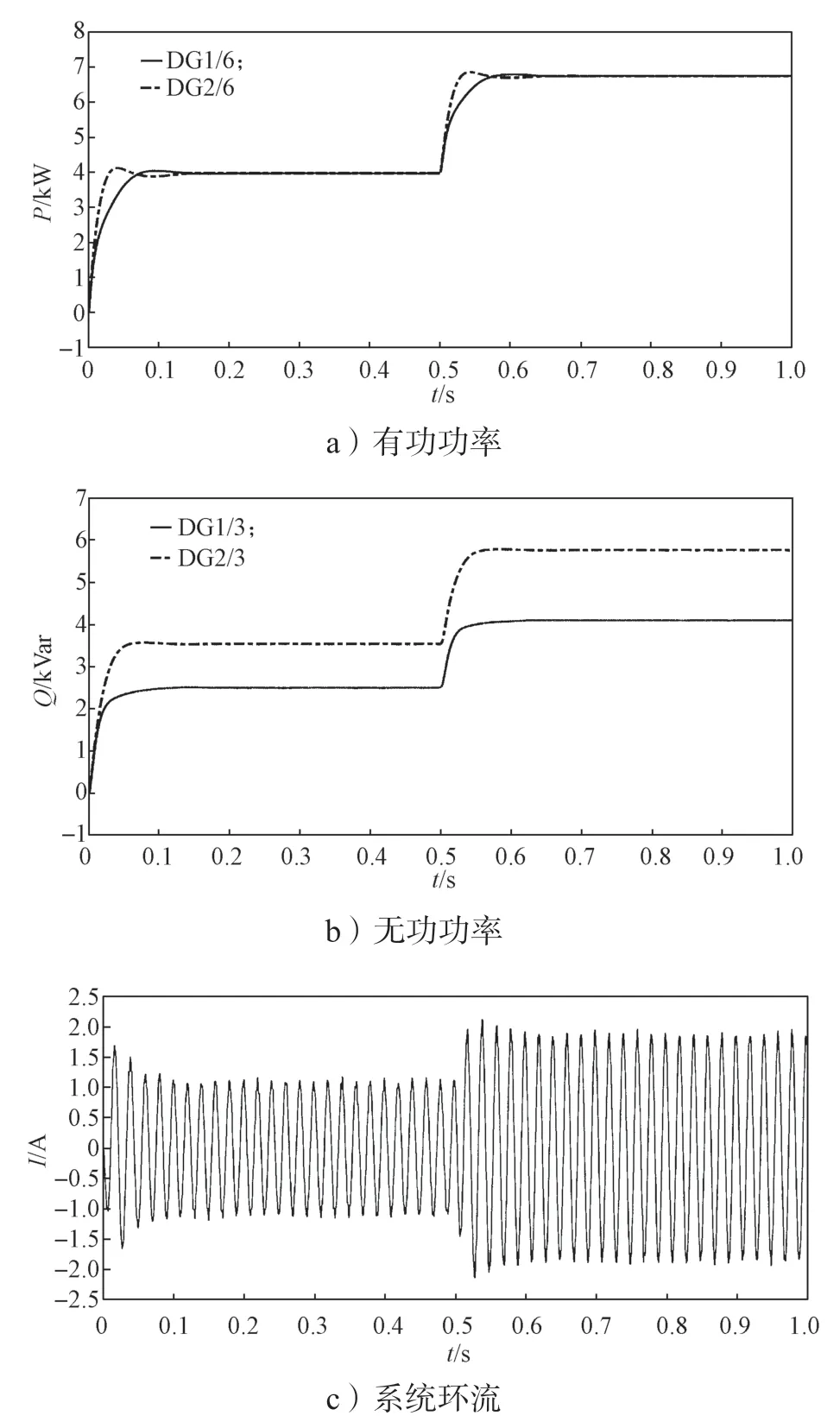
图6 传统下垂控制仿真结果Fig.6 Traditional droop control simulation results

由图6可以得知，系统仿真开始后，微电网在较短的时间（0.1 s）内达到平衡，在0.5 s 时加入公共负载后，系统也能够在较短的时间内达到稳定状态。在0～0.5 s 时，DG1 和DG2 输出的有功功率均为3.97 kW，DG1 输出无功功率为2.49 kVar，DG2 输出无功功率为3.54 kVar，系统环流稳定在1.13 A；在0.5～1.0 s 时，DG1 和DG2 输出的有功功率均为6.74 kW，DG1 输出的无功功率为4.09 kVar，DG2 输出的无功功率为5.75 kVar，系统环流稳定在1.87 A。

因为两台逆变器的线路阻抗不同，根据上文分析有功功率受影响不大，仍然可以实现完全均分；但无功功率会受到影响，导致不能均分的情况，并且较小线路阻抗的DG 单元会承担较大的无功功率，同时也会产生较大的无功环流。从图6可以看出，有功功率实现了完全均分，无功功率按照线路阻抗的反比承担功率，输出功率差值越大，产生的环流越大。

4.2 改进下垂控制策略仿真分析

采用改进的下垂控制策略进行仿真，虚拟电阻阻值为0.01 Ω，仿真结果如图7所示。

图7 改进的下垂控制仿真结果Fig.7 Improved droop control simulation results

由图7可以得知，在0～0.25 s 时，只采用加入虚拟阻抗的控制策略，0.25 s 后采用改进无功环的下垂控制策略。在0～0.25 s 时，DG1 和DG2 输出的有功功率均为3.83 kW，DG1 输出的无功功率为3.17 kVar，DG2 输出的无功功率为2.65 kVar，系统环流约为0.59 A；在0.25～0.50 s 时，DG1 和DG2 输出的有功功率均为3.95 kW，DG1 和DG2 输出的无功功率均为3.00 kVar，系统环流约为0.03 A；0.5～1.0 s 时，DG1 和DG2 输出的有功功率均为6.70 kW，DG1 和DG2 输出的无功功率均为4.90 kVar，系统环流稳定在0.11 A。

由上述分析可以得出，线路阻抗不同只能引起无功功率的不完全均分，而与有功功率是否均分无关。比较图6a 和图7a 可以看出，采用虚拟阻抗法后，系统的超调量减小，稳定速度明显加快、但是产生的电压降落直接导致了输出的有功功率下降。从图7a 可以看出，在0.25 s 时，采用改进的下垂控制策略，电压得到回升，输出功率有所提高。

比较图6b 和图7b 可以看出，在采用虚拟阻抗后，无功功率的差值有所减小，但仍然无法达到均分的效果，在0.25 s 采用改进的下垂控制策略后，无功功率可以实现均分。同时，根据图6c 和图7c 的系统环流波形，在采用虚拟阻抗后，由于输出无功功率的差值缩小，环流从1.13 A 降至0.59 A，在采用改进控制策略后，输出无功功率达到均分，环流进一步减小至0.03 A，即使增加了公共负荷，环流也稳定在0.11 A。

5 结语

本研究采取基于虚拟阻抗改进的下垂控制法，来解决因线路阻抗差异导致的无功功率分配不均、环流过大等问题。加入虚拟阻抗使逆变器等效输出阻抗呈感性，保证下垂控制法可以被应用在低压逆变器并联系统中，然后对无功环添加了电压补偿环节进行改进，使功率均分效果更好。该控制策略保留了传统下垂控制无需通信互联线路的优点，且易于实现。通过仿真分析得出，系统的动态响应速度快，超调量小，能够精确实现无功功率均分，减小了因虚拟阻抗引起的功率损耗，同时减小了系统的环流。