非对称悬臂施工曲线连续刚构桥不同施工阶段变形特性研究

杨果林，黎 勇，谭文杰，周伏良

（1.中南大学 土木工程学院，湖南 长沙 410075；2.中建五局土木工程有限公司，湖南 长沙 410004）

0 引言

随着我国交通事业以及城市建设的不断发展，国家对于桥梁施工的要求越来越高，对于桥梁的设计也越来越精细。同时，科学技术的不断创新和提高，使得我国的桥梁技术和施工水平取得了重大突破与发展[1]。桥梁施工过程中，曲线连续刚构桥相比直线型连续刚构桥，在结构线形和内力变化中有许多的不同之处，如线形变换定理在曲线连续刚构桥中将会失去效果，导致曲线连续刚构桥的施工难度比直线型连续刚构桥要大很多[2-7]。

目前，许多学者对曲线连续刚构桥的变形进行了研究，如汪永田[8]对大跨径的高墩曲线桥在悬臂施工过程中的变形情况进行了研究，得知悬臂施工时，总和工况变形曲线的梁体竖向位移最大值发生在距悬臂端1/5 悬臂长度处；吕海燕等[9]对高墩大跨PC曲线连续刚构桥在施工过程中的受力和变形情况进行了研究，得知高墩对曲线连续刚构桥的竖向位移、横向位移和扭转的影响都较大；王帆等[10]对曲线连续刚构桥的变形和受力特性进行了分析，得出恒载作用下弯梁竖向变形与直梁相差不足3%，而活荷载作用下直梁竖向位移比弯梁竖向位移大的结论。

多数学者对曲线连续刚构桥的变形研究均是在对称悬臂施工过程中开展，而对非对称悬臂施工曲线连续刚构桥的变形研究相对较少，故本研究拟以桐溪路景观桥为研究对象，分析非对称悬臂施工曲线连续刚构桥在不同施工阶段中的变形情况，以期为实际工程应用提供借鉴。

1 工程背景

桐溪路景观桥位于湖南省长沙市大王山旅游度假中心，属于坪塘大道至潇湘大道东线道路工程中的一段，为长沙市重点基础设施工程。桐溪路景观桥的主桥布置图见图1，主桥平面图见图2。

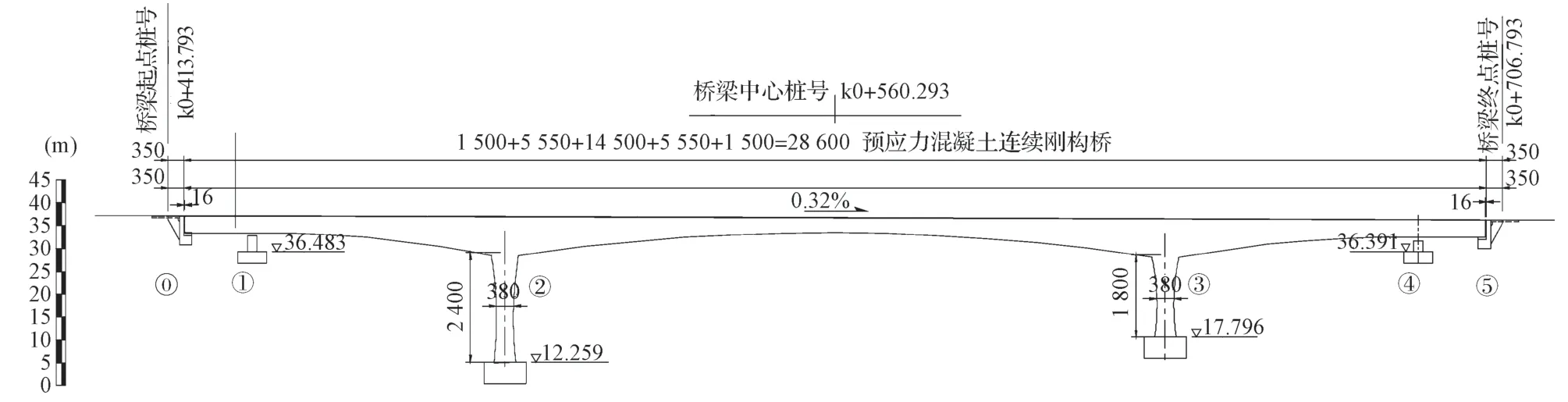
图1 主桥布置图Fig.1 Layout of the main bridge

图2 主桥平面图Fig.2 Planar graph of the main bridge

桐溪路景观桥属于新建桥梁，如图1所示，其起点桩号和终点桩号分别为k0+413.793 和k0+706.793，图1中数据单位为cm，后同。桐溪路景观桥全长约为293 m，桥梁跨径组成为15.0 m+55.5 m+145.0 m+55.5 m+15.0 m，主线宽度为22.6 m，景观平台宽5.3 m。由于该工程位于岩溶发育地区陡峭岩壁边缘，所以设计中采用曲线桥穿越矿坑，平面线型为圆曲线，桥梁平面曲线半径为600 m，主桥平面图见图2。

该桥采用挂篮悬臂现浇法进行对称及非对称施工，0#梁段采用托架现浇完成，其余各梁段采用挂篮悬臂浇筑，主梁合拢顺序为先边跨后中跨合拢。中跨悬臂浇筑的分块编号如图3所示，边跨悬臂浇筑段的分块编号如图4所示。

图3 中跨梁段分块编号Fig.3 Block number of the mid-span beam segment

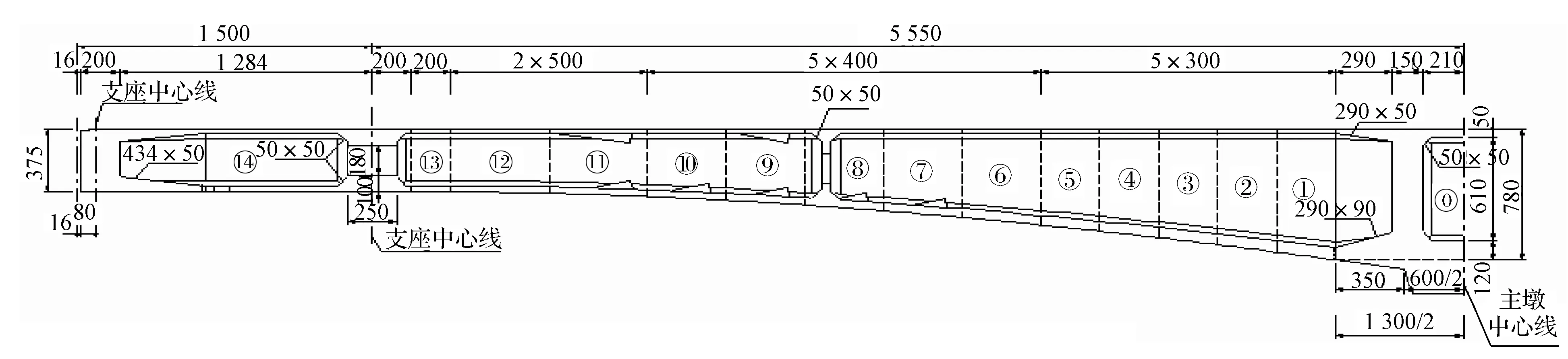
图4 边跨梁段分块编号Fig.4 Block number of the side span beam segment

2 模型建立

本研究中，采用有限元分析软件Midas/civil 建立曲线连续刚构桥模型，全桥共有110 个单元和122个节点，其具体分布如图5所示。桐溪路景观桥的整体坐标系以跨中梁段对称面为坐标系的yoz平面；坐标原点取对称面与道路中心线的交点，即对称面的中点；x轴取对称面法线方向，从2#主墩指向3#主墩；y轴指向背离曲线圆心方向；z轴指向上方。为了能够更好地模拟桥梁在不同施工阶段的变形状态，本研究中的桥模拟遵循现场施工阶段进行，对各个阶段的变形进行计算与分析。具体的施工阶段划分情况如表1所示。

图5 曲线连续刚构桥梁模型Fig.5 Curved continuous rigid frame bridge model

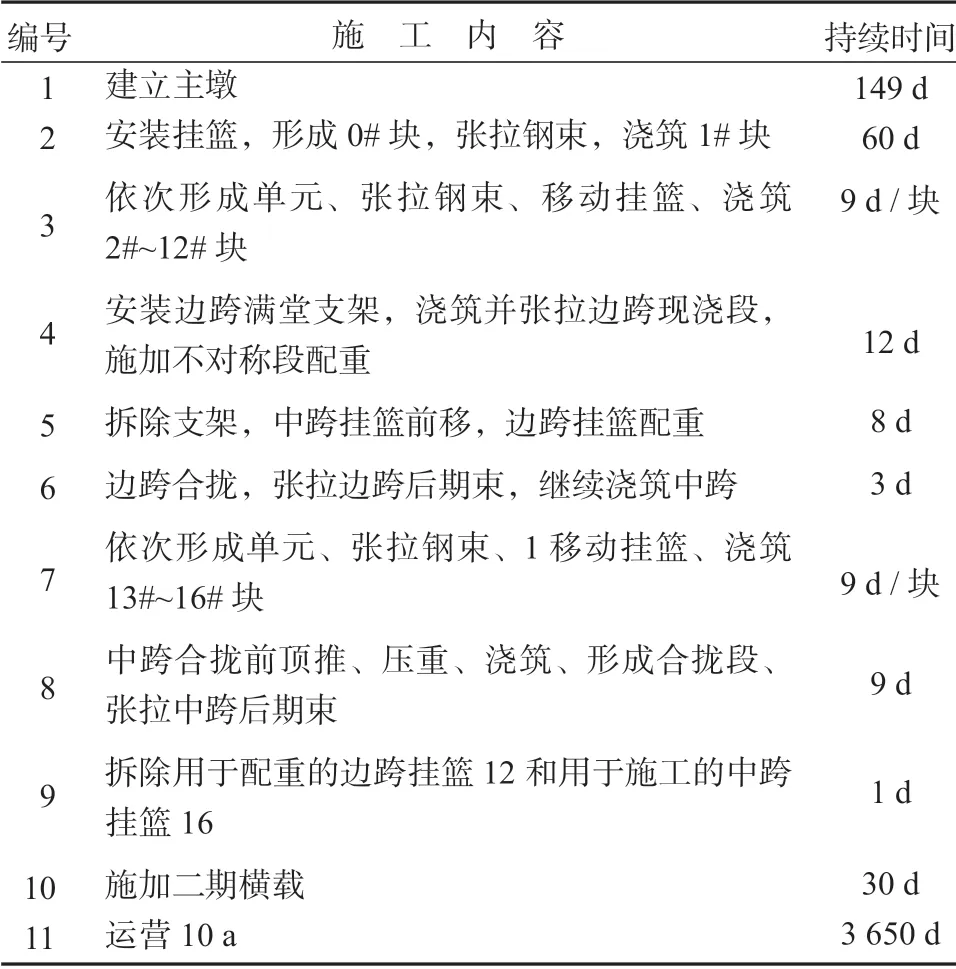
表1 施工阶段划分Table 1 Division of construction stages

在所建立的桥梁模型中，把实桥的各个梁段划分为单元号，各个单元号都有相对应的梁段，因为0#梁段的应力较为复杂，故将其划分为5 个单元，单元号与梁段的对应情况见表2。

表2 单元号与梁段对应表Table 2 Unit numbers with the corresponding table of beam segment

3 不同施工阶段下的变形分析

曲线连续刚构桥在空间上的受力是复杂多变的，这使得其桥梁结构的竖向位移变化不同于直线型连续刚构桥的，这也是一个值得深入研究的问题。在Midas/civil 计算模型中，可以根据施工顺序来定义施工阶段，从而可以分析不同施工阶段的桥梁结构线形的变化趋势。然后根据得出的线形变化趋势，可以在悬臂施工过程中提供准确的预拱度理论值，以保证成桥状态符合预期目标。本研究的Midas/civil 曲线连续刚构桥模型中，考虑了结构的自重、挂篮前移以及预应力钢束张拉等工况，分析各工况下该桥梁在悬臂施工阶段的竖向位移情况。

3.1 对称施工阶段主梁变形分析

通过Midas/civil 计算模型得到的对称施工阶段各梁段的竖向位移，如图6所示。

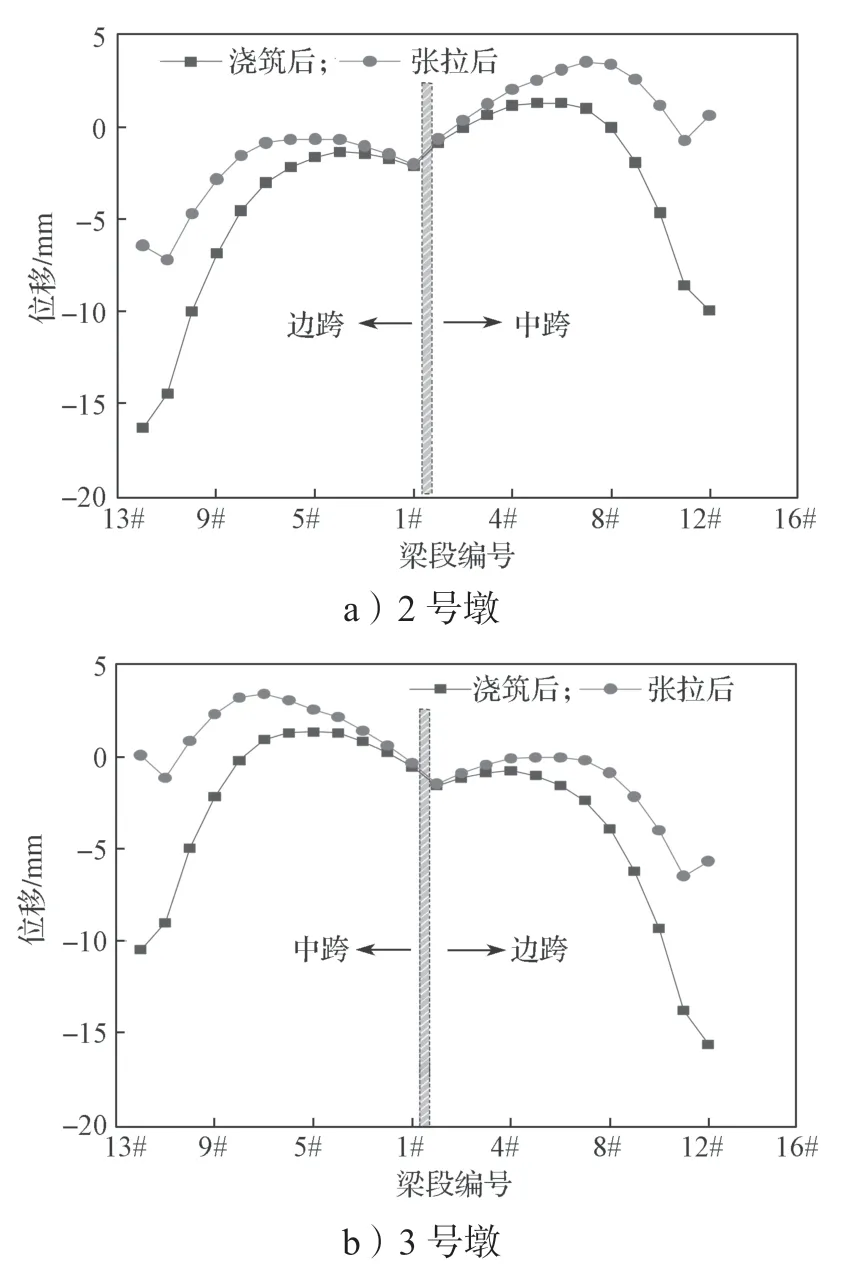
图6 对称施工阶段各梁段的竖向位移曲线Fig.6 Vertical displacement of each beam segment in a symmetrical construction

由图6可以看出，在对称施工阶段，桥梁的竖向位移变化整体呈现出随着悬臂长度的增加而增大的变化趋势。其中。最大位移处于2 号墩或者3 墩边跨的12#梁段。2 号墩边跨12#梁段浇筑后的最大竖向位移达16.3 mm，张拉后的最大竖向位移为6.4 mm；3 号墩边跨12#梁段浇筑后的最大竖向位移为15.6 mm，张拉后的最大竖向位移达到了5.6 mm。在2 号墩边跨3#梁至5#梁段中间，箱梁的竖向位移出现了一小段上挠，这是由于在施工过程中不断调整预拱度所引起的，故在桥梁施工过程中，一定要给出精确的预拱度，以保证桥梁线形符合设计要求。

从图6中还可以看出，在对称施工阶段中，2 号墩和3 号墩上边跨梁段竖向位移与中跨梁段竖向位移并不一致，边跨梁段的竖向变形量要比中跨梁段的变形大，这可能是由于临时施工荷载的不确定性或者是桥梁桥墩沉降均匀性所导致的，故在曲线连续刚构桥施工过程中，对于桥梁进行线形监控时，不仅需要考虑其临时荷载对桥梁的影响，而且要密切关注桥梁下部结构的变形情况。

3.2 非对称施工阶段主梁变形分析

通过Midas/civil 计算模型得到的非对称施工阶段各梁段的竖向位移，如图7所示。

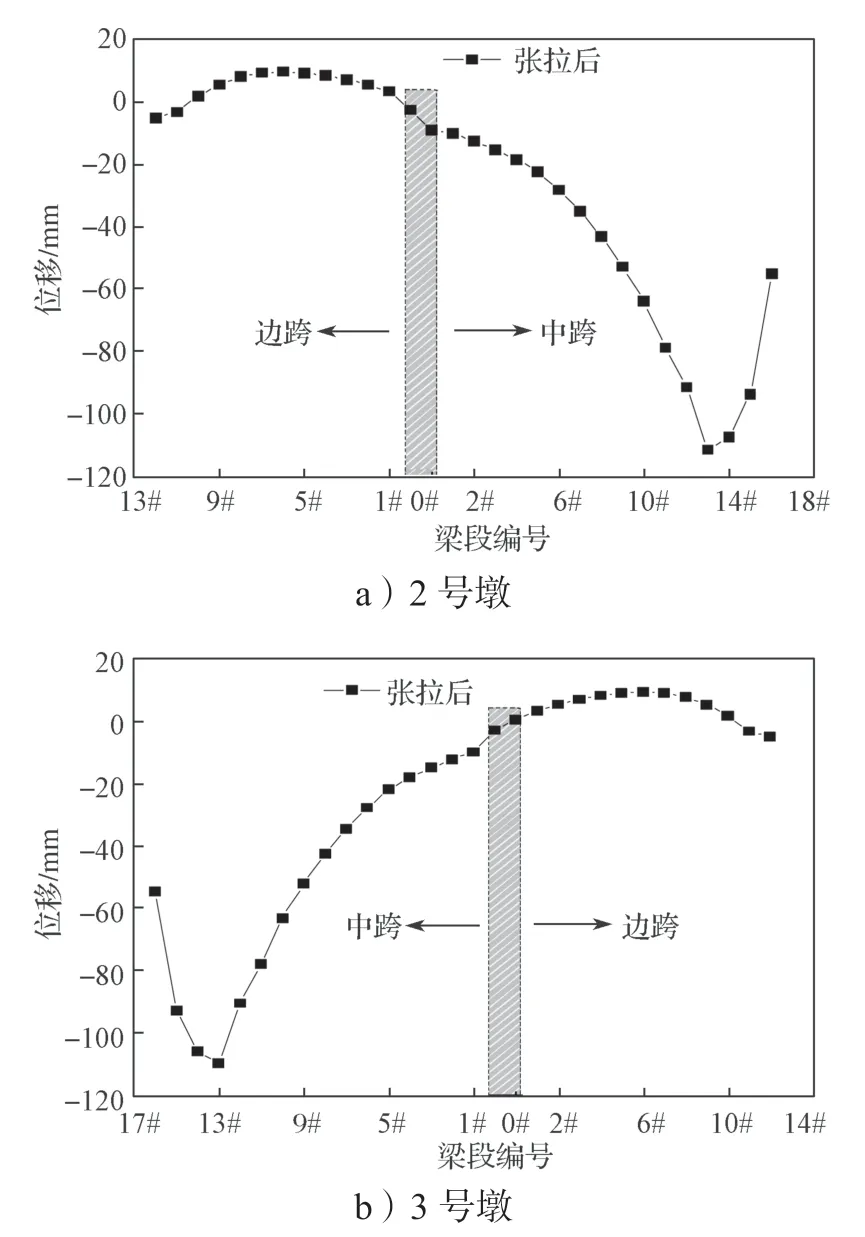
图7 非对称施工阶段各梁段的竖向位移曲线Fig.7 Vertical displacement of each beam segment in an asymmetric construction

边跨合拢后，桥梁由对称施工阶段转换为非对称施工阶段，由图7可以看出，此时桥梁的竖向变形规律呈现出不同的变化趋势，箱梁的最大位移并不是处于最大悬臂长度16#梁段上，而是位于2 号墩或3号墩上的13#梁段，2 号墩13#梁段的最大竖向位移为112.1 mm，而最大悬臂长度16#梁段的竖向位移仅为55.1 mm。对比图6和图7可以得知，在进入非对称阶段施工后，2 号墩或者3 号墩的边跨7#梁段附近的竖向位移有明显的上挠情况，而中跨箱梁位移有明显的下挠情况，这是由于非对称阶段的增加，导致中跨自重要大于边跨自重所引起的，故在非对称施工过程中，需要注意边跨箱梁上挠及中跨箱梁下挠的情况，以避免产生位移过大而导致箱梁出现开裂的现象。本桥采用的是悬臂浇筑进行施工，但是桥梁结构并不完全是对称结构，待桥梁对称阶段施工完成并且进行边跨合拢后，就需要对非对称阶段（13#～16#）进行施工，因此，需要分析在非对阶段施工过程中其对已经完成的对称阶段箱梁的影响。上述论述中提到了在非对称施工阶段中，施工对边跨7#梁段的竖向位移影响最大，故取边跨6#梁段和7#梁段的竖向位移进行分析，得到的非对称阶段施工对边跨箱梁竖向位移的影响曲线如图8所示。

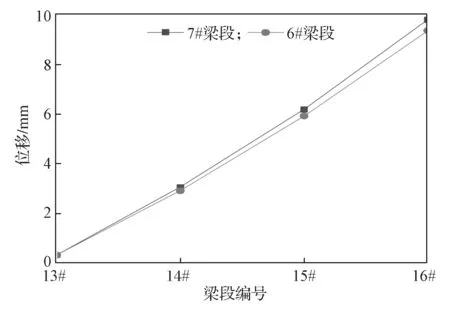
图8 非对称阶段施工对边跨箱梁竖向位移的影响曲线Fig.8 Influence of asymmetric construction on vertical displacement of the side span box girder

由图8可以得知，边跨6#和7#梁段的位移上挠值随着非对称阶段梁段数的增加呈现出线性增长的变化趋势，其中7#梁段上挠程度要略大于6#梁段的。在中跨13#梁段施工完成后，6#梁段的竖向位移为0.331 mm，7#梁段的竖向位移为0.327 mm，在中跨16#梁段施工完成后，6#梁段的竖向位移为9.4 mm，7#梁段的竖向位移为9.8 mm，6#梁段、7#梁段的竖向变形受非对称施工的影响，总上挠值约为9 mm。由此可以得知，非对称阶段施工对边跨中部的影响非常大，故在非对称施工阶段中，要密切注意边跨中部箱梁的变形情况。

3.3 合拢段施工完成后主梁变形分析

桥梁中跨合拢是桥梁施工的一个重点与难点，为了确保桥梁顺利合拢，需要严格控制梁体的变形情况。中跨合拢后，梁体的变形也会发生改变，为此，选取中跨合拢施工完成后的桥梁变形情况进行分析，得到的变形分析结果如图9所示。

图9 中跨合拢后各梁段竖向位移曲线Fig.9 Vertical displacement of each beam segment after the middle span closure

由图9所示中跨合拢后各梁段竖向位移曲线可以看出，中跨合拢段施工完成后，2 号墩和3 号墩中跨部分梁体的竖向变形整体出现上挠情况，合拢段施工完成后梁体的最大竖向位移均位于中跨合拢段附近。在中跨合拢段施工之前，中跨最长悬臂端的竖向位移为58 mm，中跨箱梁最大竖向位移为112 mm；在中跨合拢段施工完成后，中跨最长悬臂端箱梁的竖向位移为48 mm，中跨箱梁最大竖向位移为104 mm，这一结果表明，中跨合拢使得中跨箱梁竖向变形上挠了约10 mm。

3.4 不同施工阶段曲线连续刚构桥变形对比分析

图10～13 所示为对称施工阶段2 号墩和3 号墩处的实测高程与理论高程差值图，图中纵坐标所示误差值为桥梁施工现场实测值减去Midas/civil 模型计算理论值的差值，下图类同。

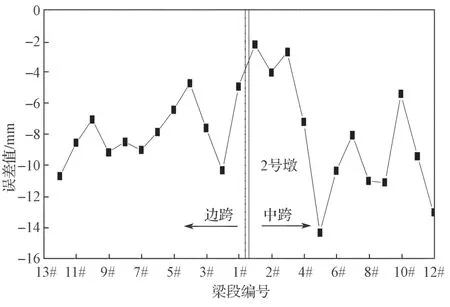
图10 对称施工阶段2 号墩处不同梁段浇筑后的竖向位移实测值与理论值误差曲线Fig.10 Error curves of the measured value and theoretical value of vertical displacement after the pouring of different beam segments of No.2 pier under a symmetrical construction

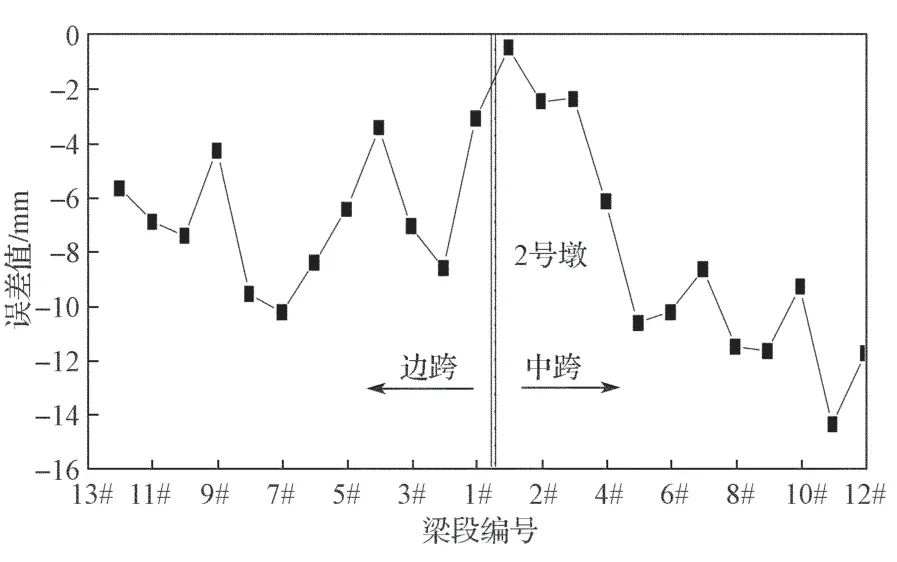
图11 对称施工阶段2 号墩处不同梁段张拉后的竖向位移实测值与理论值误差曲线Fig.11 Error curves of the measured value and the theoretical value of vertical displacement at different beam segments of No.2 pier under a symmetrical construction

由图10和图11可以得知，在对称施工过程中，2 号墩上各梁段浇筑后的竖向位移的误差最大值为14.381 mm，位于中跨5#梁段；各梁段张拉后的竖向位移误差最大值为14.351 mm，位于中跨11#梁段。由此可以得知，在对称施工过程中，2 号墩各梁段在浇筑后和张拉后的实测高程值与理论值的误差均在0～15 mm 范围之内。

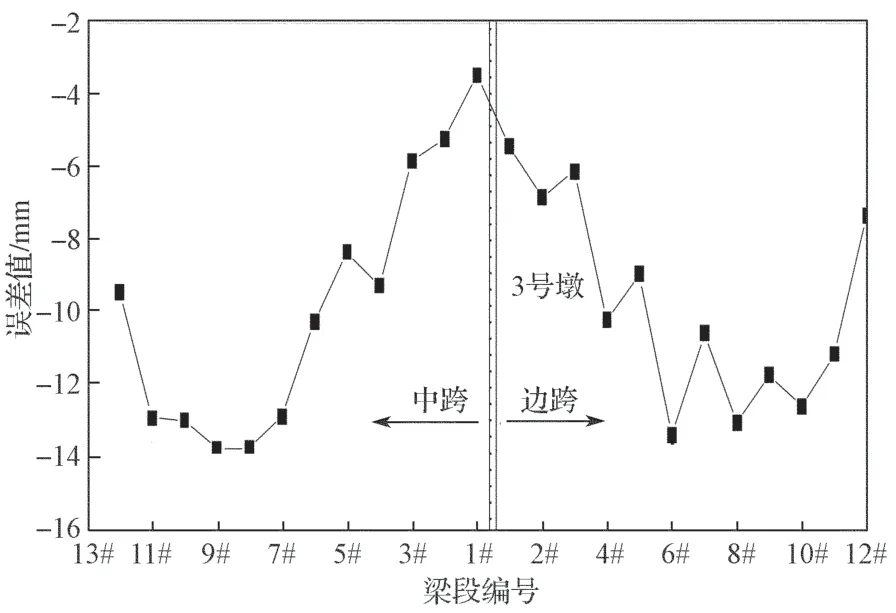
图12 对称施工阶段3 号墩处不同梁段浇筑后的竖向位移实测值与理论值误差曲线Fig.12 Error curves of the measured value and theoretical value of vertical displacement after the pouring at different beam segments of No.3 pier under a symmetrical construction

图13 对称施工阶段3 号墩处不同梁段张拉后的竖向位移实测值与理论值误差曲线Fig.13 Error curves of the measured value and the theoretical value of vertical displacement at different beam segments of No.3 pier under a symmetrical construction

由图12和图13可以得知，在对称施工过程中，3 号墩各梁段浇筑后的竖向位移误差最大值为13.847 mm，各梁段张拉后的竖向位移误差最大值为14.873 mm，由此可见，浇筑后和张拉后3 号墩各梁段的实测高程值与理论值之间的误差也均在0～15 mm 范围之内。根据线形监控允许误差表得出，本桥的允许误差值为±29 mm（即145 m/5 000），故根据已有结果可以得知，2 号墩和3 号墩张拉后的误差值都在允许误差范围之内，说明在对称施工阶段和张拉后的线形都符合设计要求。

由图12和图13还可以得知，在混凝土浇筑后或者预应力张拉后，高程误差值随着梁段数的增加而增大，误差较大处位于非对称阶段，0#梁段附近的误差最小。由此可知，在现场施工过程中，对箱梁变形出现的误差的修正并不是很精确，故在类似工程中，对出现的误差值要及时修正并进行验算，以提高线形控制精度。

图14所示为非对称施工阶段不同梁段的实测位移与理论位移误差曲线。

图14 非对称施工阶段不同梁段的实测位移与理论位移误差曲线Fig.14 Error curves of the measured displacement and theoretical displacement at different beam segments under an asymmetric construction

由图14a 可以得知，非对称施工阶段中，2 号墩各梁段浇筑后的实测竖向位移与理论竖向位移的误差值在-22～7 mm 范围内，张拉后的实测竖向位移与理论竖向位移的误差值在-4.9～-19.1 mm 范围内，均小于±29 mm。由图14b 可以得知，3 号墩各梁段浇筑后的实测竖向位移与理论竖向位移的误差值在-4.9～24.8mm 范围内，张拉后的实测竖向位移与理论竖向位移的误差值在-5.6～-23.7 mm 范围内，均小于±29 mm，说明在非对称悬臂施工过程中，桥梁各梁段浇筑后和张拉后的变形量均符合设计要求。

本桥在施工过程中的允许误差值为±29 mm，但是在非对称悬臂施工过程中，最大竖向位移误差值达到了24.8 mm，而在对称悬臂施工过程中，最大竖向位移误差值约为14.9 mm，故可以看出，在非对称悬臂过程中产生的误差值要比在对称悬臂施工过程中产生的误差值约大10 mm，说明桥梁在非对称悬臂施工过程中，桥梁结构线形控制的难度要大于对称悬臂施工阶段的。因此，在非对称悬臂施工过程中，需要加强对线形的监控，保证误差值较小，以达到线形控制效果良好。

4 设计参数对梁体竖向位移的影响

4.1 混凝土容重对梁体竖向位移的影响

结合现场施工时的实际情况，分别取超过混凝土容重设计值幅度的2%,3%,5%，在16#梁段施工完成后，对各梁段产生的竖向位移进行对比分析，所得2号墩中跨各梁段的变形分析结果如图15和图16所示。

图15 不同容重下2 号墩中跨各梁段的竖向位移曲线Fig.15 Vertical displacement of each beam segment in the middle span of No.2 pier under different bulk densities

图16 不同容重下2 号墩中跨各梁段竖向位移的相对变化率曲线Fig.16 Relative change rate of vertical displacement of each beam segment of mid span at No.2 pier under different bulk densities

由图15所示不同容重下2 号墩中跨各梁段的竖向位移曲线可以得知，混凝土容重的变化会引起箱梁梁体的竖向位移发生变化。随着混凝土容重的增加，箱梁梁体的竖向位移增加，各梁体的竖向位移最大值位于非对称阶段第一块（中跨13#梁段）。当混凝土的容重提高2%时，箱梁的最大竖向位移为115.3 mm；当混凝土的容重提高3%时，箱梁的最大竖向位移为117.1 mm；当混凝土的容重提高5%时，箱梁的最大竖向位移为120.7 mm。

由图16所示不同容重下2 号墩中跨各梁段竖向位移的相对变化率曲线可以得知，混凝土容重的变化对箱梁梁体的竖向位移变化呈线性关系，当混凝土的容重提高2%时，相对于混凝土标准容重设计值下的梁体最大竖向位移值提高了3.23%，最大相对变化率为4.79%，位于中跨6#梁段；当混凝土的容重提高3%时，相对于混凝土标准容重设计值下的箱梁最大竖向位移值提高了4.85%，最大相对变化率为7.19%，位于中跨6#梁段；当混凝土的容重提高5%时，相对于混凝土标准容重设计值下的梁体最大竖向位移值提高了8.08%，最大相对变化率为11.98%，位于中跨6#梁段。由此可以得知，虽然混凝土容重的变化引起箱梁梁体竖向位移的最大变化处位于非对称阶段第一块，但混凝土容重的改变对箱梁梁体竖向位移的影响最大处位于中跨6#梁段，这两者的位置是不一致的。由此可知，混凝土容重的改变对对称阶段施工箱梁的竖向位移影响更大。

4.2 混凝土收缩徐变对梁体竖向位移的影响

混凝土收缩徐变对桥梁结构变形的影响是一个长期的过程，故对该工程桥梁成桥阶段和成桥10 a两个时间点的收缩徐变进行分析，并且将该竖向位移值与不考虑收缩徐变的成桥状态竖向位移结果进行对比，其分析及对比结果见图17和图18。

图17 不同状态下各梁段的竖向位移曲线Fig.17 Vertical displacement of each beam segment at different states

由图17所示不同状态下各梁段的竖向位移曲线可以得知，在不考虑收缩徐变作用和考虑收缩徐变作用两种条件下，成桥状态考虑收缩徐变作用的桥梁结构的竖向位移要比不考虑收缩徐变作用的桥梁结构的竖向位移大。从图17中还可以看出，对于考虑收缩徐变作用时，成桥10 a 的桥梁结构的竖向位移要增大许多。

图18所示为考虑收缩徐变与不考虑收缩徐变时各梁段的竖向位移差值曲线，图中的竖向位移差值为考虑收缩徐变不同状态下各梁段的竖向位移值减去不考虑收缩徐变成桥状态下各梁段的竖向位移值。由图18可以看出，在考虑收缩徐变作用和不考虑收缩徐变作用这两种状态下，箱梁梁体的竖向位移差值变化比较大。

图18 考虑收缩徐变与不考虑收缩徐变各梁段的竖向位移差值曲线Fig.18 Vertical displacement difference of each beam segment with or without a consideration of the shrinkage and creep

综合图17和图18可以得知，成桥状态中，在中跨合拢段附近的梁段的竖向位移差值相对较大，最大差值为18.66 mm，不考虑收缩徐变作用成桥状态的最大竖向位移为87.2 mm，考虑收缩徐变作用成桥状态的最大竖向位移为104.5 mm。由此可以得知，在考虑收缩徐变影响的梁段最大竖向位移值比不考虑收缩徐变影响的最大竖向位移值提高了19.8%；在成桥10 a 状态中，箱梁梁体的竖向位移最大差值为96.3 mm，箱梁梁体最大竖向位移值为176.4 mm，相比不考虑收缩徐变影响的梁段最大竖向位移值增加了89.2 mm。

从以上的分析结果可以得知，混凝土收缩徐变对桥梁结构的竖向变形有着较大的影响，尤其是在桥梁中跨跨中附近，混凝土收缩徐变对梁段的竖向变形影响明显。因此，在桥梁设计中，必须重视桥梁中跨跨中附近箱梁的竖向变形。

4.3 曲率半径对梁体竖向位移的影响

通过研究分析可知，曲线连续刚构桥在中跨合拢后，箱梁最大的竖向位移位于2#墩和3#墩的中跨梁段处，故选取2#墩和3#墩中跨梁段的竖向位移进行分析，其变形分析结果见图19。

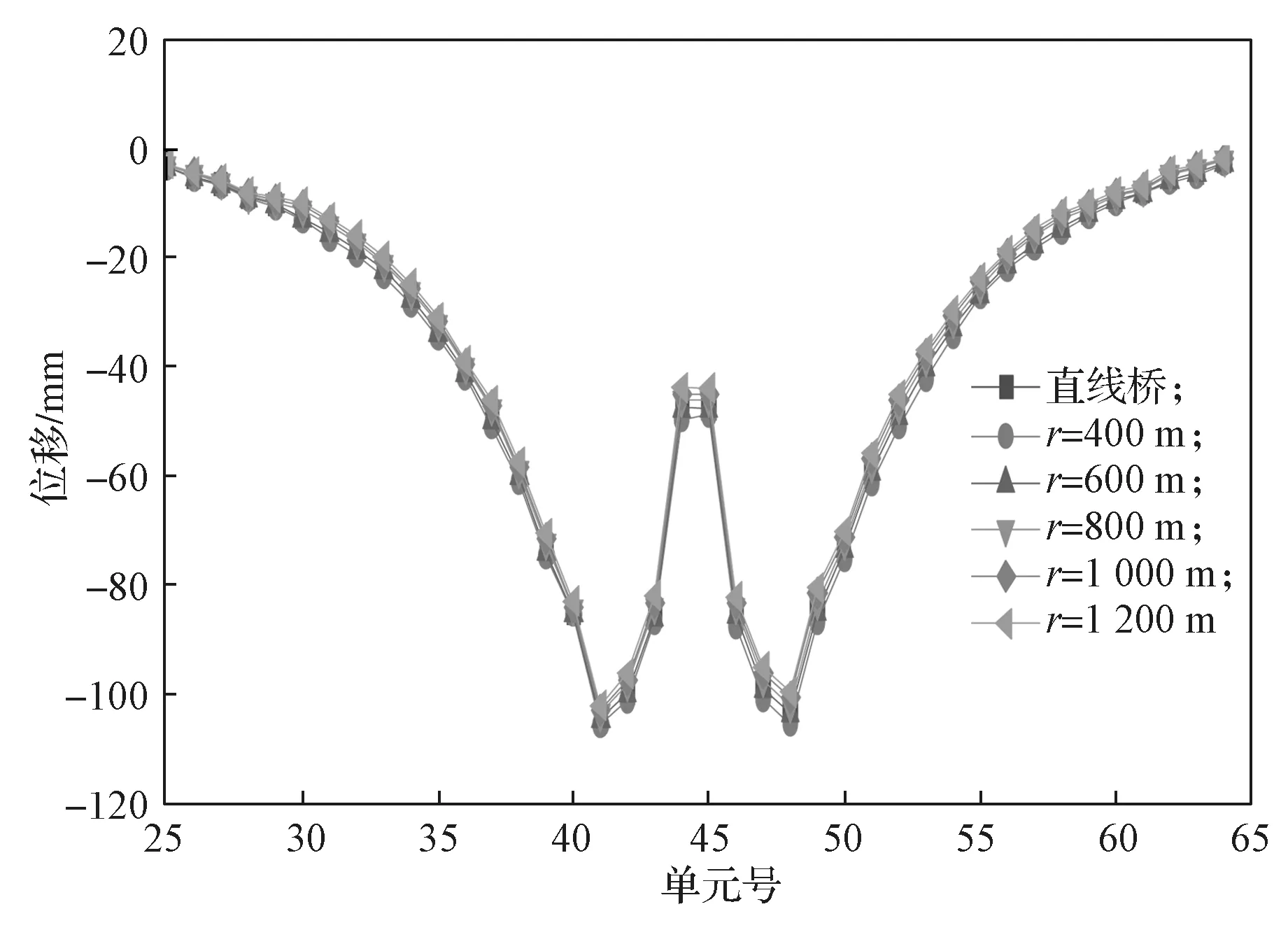
图19 中跨合拢后跨中不同梁段的竖向位移曲线Fig.19 Vertical displacement of different beam segments in the mid-span after the mid-span closure

由图19可以得出，跨中处的箱梁竖向位移随着曲率半径的增大而减小，减小幅度较大处位于非对称施工阶段以及中跨合拢段。曲线连续刚构桥跨中部分箱梁的竖向位移随着曲率半径的增大而减小，但是这种减小趋势并不是很明显，当曲率半径增大到1 200 m 时，曲线连续刚构桥跨中处箱梁的竖向位移仅减小了12%。

上面仅分析了曲率半径对竖向位移的影响，为了更好地分析曲率半径对梁体横向位移的影响，选取2#墩和3#墩中跨梁段的横向位移进行分析，所得变形分析结果如图20所示。

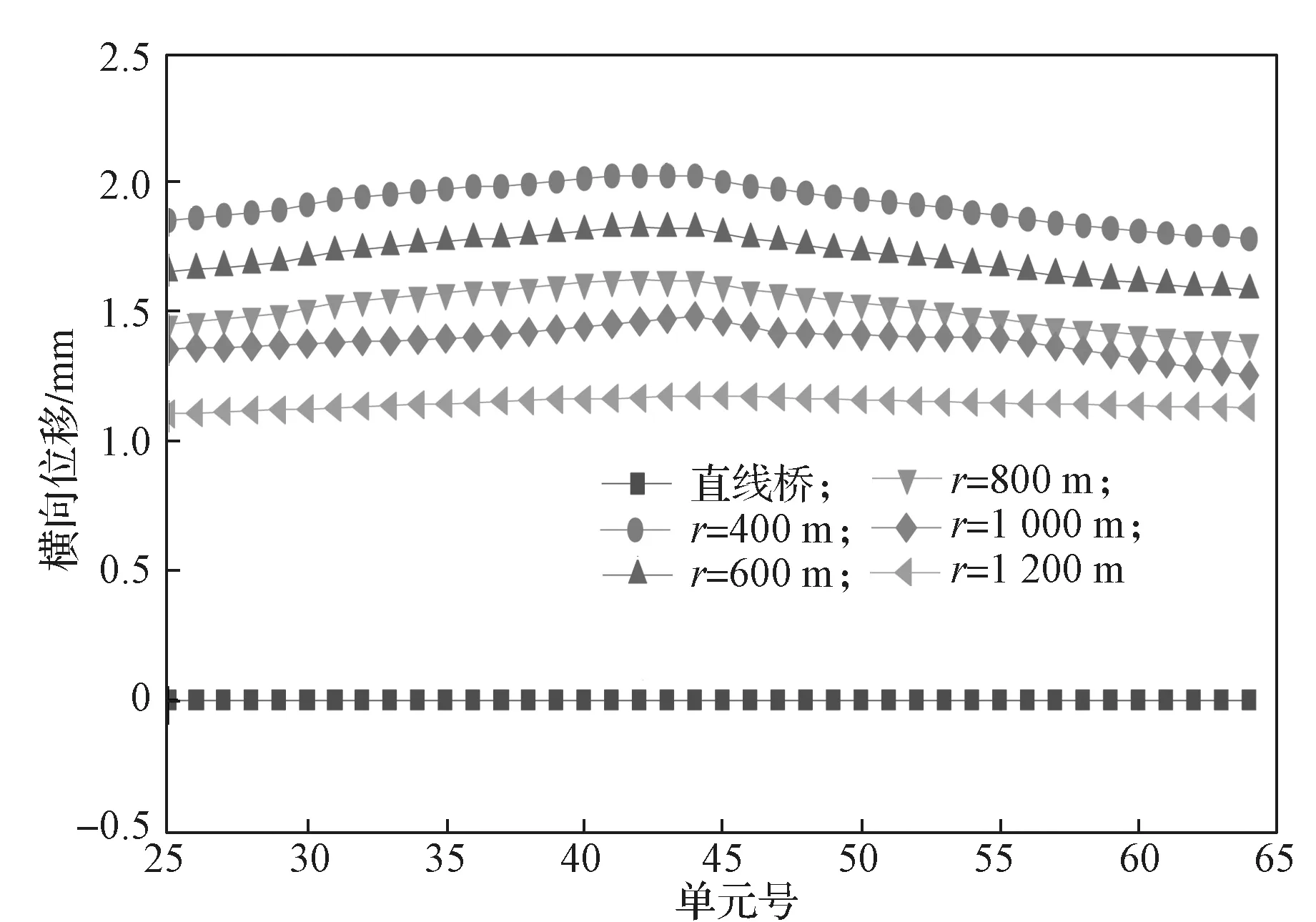
图20 中跨合拢后不同梁段的横向位移曲线Fig.20 Transverse displacement of different beam segments after the mid-span closure

由图20可以得知，曲线连续刚构桥在中跨合拢后，跨中箱梁的横向位移会随着曲率半径的增大而逐渐减小，且其减小趋势随着曲率半径的增大而变得缓慢，当曲率半径趋向无穷大时，即直线桥时，跨中箱梁基本上不会产生横向位移。即曲线连续刚构桥跨中处箱梁的横向位移是随着曲率半径的增大而减小的，并且其横向位移减小的幅度较大。当曲率半径达1 200 m 时，2 号墩的15#梁段的横向移位减小幅度高达87%。

5 结论

1）在桥梁对称施工过程中，箱梁竖向位移随着悬臂长度的增加而增大；在桥梁对称施工阶段中，2号墩和3 号墩上边跨箱梁的竖向位移与中跨的竖向位移变化量并不一致，边跨箱梁的位移要大于中跨箱梁的位移。

2）非对称施工阶段时，施工会对边跨中部附近的箱梁引起较大的上挠现象，非对称阶段施工完成后，箱梁的最大上挠位移值达10 mm，因此，在非对称阶段施工过程中，需重点关注边跨中部附近箱梁的竖向变形情况。

3）中跨合拢后，箱梁的竖向变形呈现出整体的上挠现象，上挠最明显的部位位于中跨合拢段附近。

4）在非对称施工阶段中产生的变形误差值要大于对称施工阶段产生的变形误差值，故在非对称阶段施工过程中，需着重加强对桥梁线形的监控，同时及时对产生的误差进行修正，以提高施工精度。

5）在非对称施工阶段中，混凝土自重对桥梁结构竖向位移的影响最大，因此在非对称施工过程中必须严格控制混凝土自重的偏差，提高监控精度。混凝土收缩徐变对桥梁结构线形在成桥后有较大的影响，且主要位于中跨跨中位置。因此，在后期的桥梁维护中，要重点观察桥梁跨中附近箱梁的竖向变形，以保证桥梁结构的安全。

6）在中跨合拢完成工况下，曲线连续刚构桥随着曲率半径的增大，其竖向变形和横向变形都会随之改变，呈现出随曲率半径增大而逐渐变小的变化趋势，这体现了曲线连续梁桥独有的“弯扭耦合”受力特性。在曲率半径由400 m 增大至1 200 m 的变化过程中，箱梁横向位移变化的趋势随着曲率半径的增大而越来越缓慢；箱梁竖向位移随着曲率半径的增大而减小，但减小幅度较小，曲率半径对箱梁竖向变形的影响主要位于非对称施工阶段和中跨合拢段。