基于分形维与自相关函数绝对值均值的端点检测算法
2021-05-07陈航伍子嘉彭勇宋威
陈航 伍子嘉 彭勇 宋威


摘 要:在语音信号处理中,端点检测是语音处理的一个重要部分。现提出一种基于分形维数和语音帧自相关函数绝对值均值的双门限端点检测方法。根据语音信号和噪声信号分形维的不同,以及噪声信号与语音信号自相关函数的特点进行语音端点检测,并通过MATLAB仿真进行验证。实验结果表明,该方法在5 dB噪声环境下能较好地判断语音信号的起止点。
关键词:端点检测;分形维数;自相关函数绝对值均值
中图分类号:TN92 文献标志码:A文章编号:2096-4706(2021)21-0108-04
Abstract: In speech signal processing, endpoint detection is an important part of speech processing. In this paper, a dual-threshold endpoint detection method based on the fractal dimension and the absolute mean value of the speech frame autocorrelation function is proposed. According to the different fractal dimensions of speech signal and noise signal and the characteristics of autocorrelation function of noise signal and speech signal, the speech endpoint is detected and verified by MATLAB simulation. Experimental results show that this method can better judge the start and end points of speech signals in 5 dB noise environment.
Keywords: endpoint detection; fractal dimension; absolute mean value of autocorrelation function
0 引 言
語音端点检测是语音识别中的一个重要部分,用于准确地判断含有噪声语音信号的起止点[1]。随着机器学习、神经网络的发展,语音识别也越来越受到人们的重视,语音识别中端点检测是极其重要的一环,端点检测的正确率会直接影响到后续语音识别的准确率。研究表明,即使是在十分安静的环境下,语音识别也不可能百分之百准确,语音检测系统中超过一半以上的错误可能来自端点检测[2]。因此,对端点检测的研究具有十分重要的意义。传统的语音检测方法主要是基于短时能量和短时过零率的双门限检测方法,双门限法对含有白噪声语音的检测效果很好。然而,现实世界中的噪声是复杂多变的,致使双门限法有时候也难以达到预期的效果[3],为此许多学者对其进行了改进。薛胜尧[4]出于提高识别率的目的,提出一种通过调整阈值个数,引入语音结束最小长度的方法对其进行改进。邓艳容等[5]提出先利用谱减法去噪,然后采用双门限法进行判断。朱利春[6]等提出基于LMS自适应滤波进行判断的方法。专家们所提的这些方法都取得了较好的效果。除了双门限法之外,后来学者们又提出了谱距离法、MCCF倒谱距离法、谱熵法等方法以及先降噪再进行端点检测的联合方法,也都取得了较好的效果[7]。
本文基于短时能量与短时过零率的双门限思想,提出一种新的检测方法,即结合分形维数与自相关函数绝对值均值来对语音信号进行端点检测。通过对信号进行预加重及分帧加窗处理,计算每一帧数据的分形维数和自相关函数绝对值均值。通过设置合理的门限进行判断,达到对语音端点检测的目的。
1 分形维数与自相关函数
1.1 分形维数
空气动力学的研究发现,语音信号是一种非线性信号,具有混沌的特性[8]。分形是描述混沌特性的一种重要手段,而分形维数则是分形的一个重要特征。因此,我们可以用分形维数来描述语音信号。语音分形维数常用的计算方法有Katz方法、Higuchi方法、Petrosian方法和Maragos方法[9],本文采用Katz方法进行计算。
将语音信号看成一系列的点,在坐标系中用(x,y)的形式表示出来,x代表示采样点且单调递增,y表示对应的幅值。那么语音信号的分形维数就可以用式(1)来计算:
式(2)中,wlen表示一帧语音信号的长度,xi(j+1)和xi(j)表示第i帧数据的第j+1和第j个点对应的横坐标。yi(j+1)和yi(j)则表示第i帧数据的第j+1和第j个点的幅值,式(3)中xi(1)表示第i帧数据的第一个点的横坐标,yi(1)表示第i帧数据的第一个点的幅值,其他变量与式(2)中的含义相同。式(4)中变量含义与式(1)中相同。
通过以上表达式,我们就可以计算含噪声语音信号的每一帧数据的分形维数,由表达式可知,影响分形维数的主要因素就是信号的幅值,而含有噪声的语音信号所对应的幅值往往大于单独的噪声信号的幅值,所以可以得出,含有噪声的语音信号的分形维数一般大于单独的噪声信号。图1给出了10 dB信噪比下分形维数分布图。
由图1可知,语音信号的分形维数一般大于噪声信号的分形维数,特别是语音幅度较大时,分形维数的幅值会相应地更大;语音幅值较小时,对应的分形维数也相对较小,阈值选取不当容易造成误判。
1.2 自相关函数
自相关又称序列相关,它描述的是一个信号本身在不同时刻的互相关。在信号处理中,常常被用来找出一系列数据中重复的模式(比如被噪声淹没的周期信号),也可以用来识别淹没于信号的谐波频率中的基频信号。它的函数定义可以由(5)表示:
式(6)相较于式(5)在形式上多了一个下标i,下标i表表示第i帧数帧据,其他变量与式(5)中的含义相同。
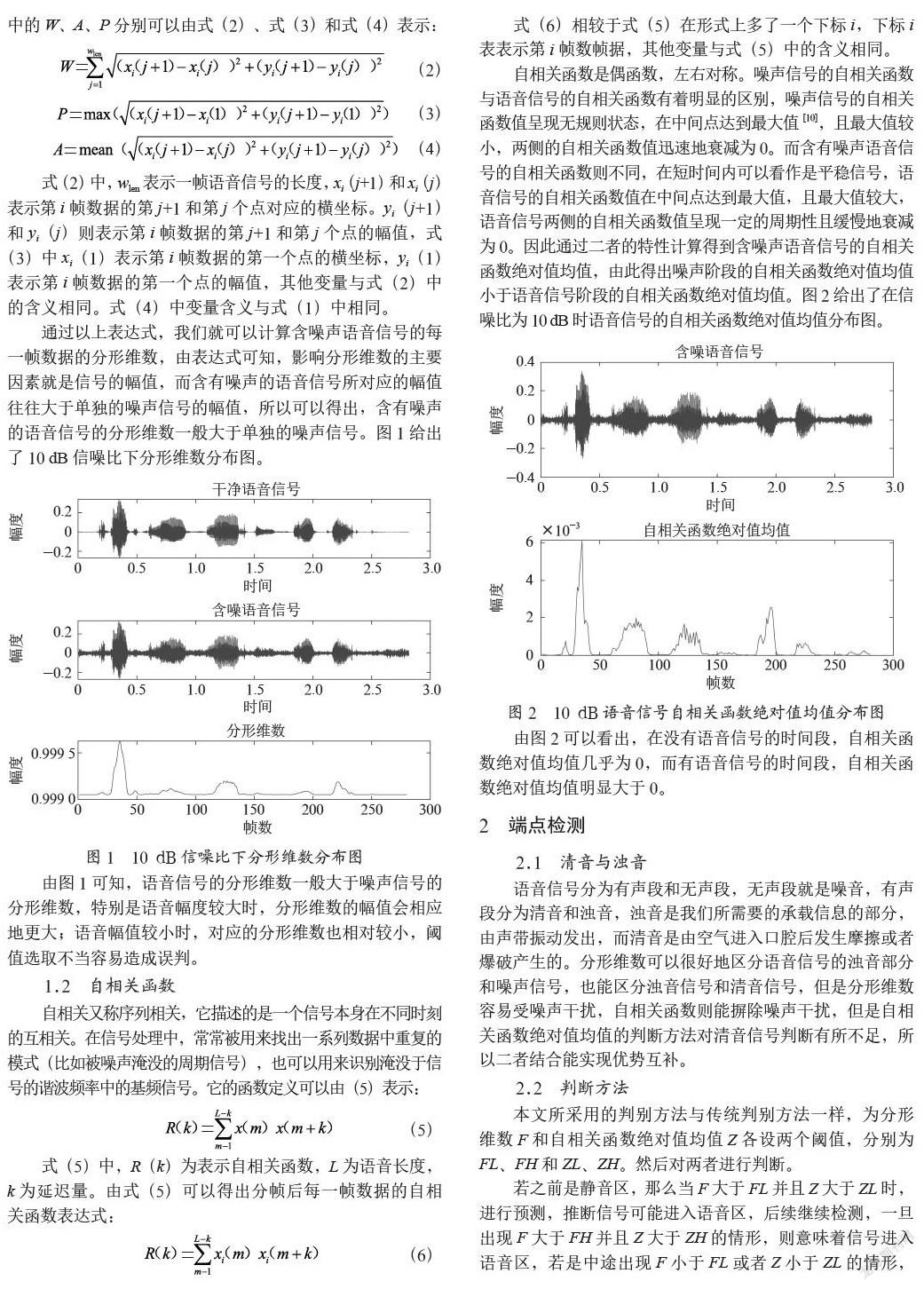
自相关函数是偶函数,左右对称。噪声信号的自相关函数与语音信号的自相关函数有着明显的区别,噪声信号的自相关函数值呈现无规则状态,在中间点达到最大值[10],且最大值较小,两侧的自相关函数值迅速地衰减为0。而含有噪声语音信号的自相关函数则不同,在短时间内可以看作是平稳信号,语音信号的自相关函数值在中间点达到最大值,且最大值较大,语音信号两侧的自相关函数值呈现一定的周期性且缓慢地衰减为0。因此通过二者的特性计算得到含噪声语音信号的自相关函数绝对值均值,由此得出噪声阶段的自相关函数绝对值均值小于语音信号阶段的自相关函数绝对值均值。图2给出了在信噪比为10 dB时语音信号的自相关函数绝对值均值分布图。
由图2可以看出,在没有语音信号的时间段,自相关函数绝对值均值几乎为0,而有语音信号的时间段,自相关函数绝对值均值明显大于0。
2 端点检测
2.1 清音与浊音
语音信号分为有声段和无声段,无声段就是噪音,有声段分为清音和浊音,浊音是我们所需要的承载信息的部分,由声带振动发出,而清音是由空气进入口腔后发生摩擦或者爆破产生的。分形维数可以很好地区分语音信号的浊音部分和噪声信号,也能区分浊音信号和清音信号,但是分形维数容易受噪声干扰,自相关函数则能摒除噪声干扰,但是自相关函数绝对值均值的判断方法对清音信号判断有所不足,所以二者结合能实现优势互补。
2.2 判断方法
本文所采用的判别方法与传统判别方法一样,为分形维数F和自相关函数绝对值均值Z各设两个阈值,分别为FL、FH和ZL、ZH。然后对两者进行判断。
若之前是静音区,那么当F大于FL并且Z大于ZL时,进行预测,推断信号可能进入语音区,后续继续检测,一旦出现F大于FH并且Z大于ZH的情形,则意味着信号进入语音区,若是中途出现F小于FL或者Z小于ZL的情形,那么就否定之前的预测,回归到靜音区的判定。
若之前是语音区,后续如果出现F小于FH或者Z小于ZH的情形,可以假设语音即将结束,如果后面出现F小于FL或者Z小于ZL的情形,那么就认为语音区结束。
3 实验验证
在计算分形维数和自相关函数之前,需要对语音信号进行预处理。语音信号的预处理分为预加重和加窗分帧处理两部分。预加重的目的是为了提升高频部分,加重之后会使得信号的频谱变得更加平坦,那么在低频到高频的整个频段中就可以使用同样的信噪比来求解频谱,方便后续的频谱分析和声道参数分析。加窗分帧处理使用汉明窗,采用交叠分帧方式进行处理,这样能使得分帧后的数据具有连续性,过渡更加自然。这里采用ZOIZEUS数据库语音信号进行实验,实验数据的采集频率为8 000 Hz,因为语音在10 ms到36 ms之间被认为是平稳的,所以我们以200个数据点为一帧数据信号(即以25 ms为一帧数据),步长为80个数据点(10 ms)。取5 dB street、airport环境下的含噪声语音信号进行实验,并将本文算法结果与传统双门限法的结果进行对比,得到的实验结果如图3所示。
从图中可以看出,5 dB噪声下,无论是airport还是street环境下,语音信号的过零率均已受到噪声的严重影响,语音信号与纯噪声部分的过零率不再出现陡峭的下降趋势,而是下降过程变得相对平缓,甚至反而升高,此时已经失去了在高信噪比时噪声信号过零率远大于语音信号过零率的特点,所以在检测中,检测结果会出现偏差甚至是错误。本文未曾在途中标出检测结果,因为过零率已经产生明显偏差,不可能得到正确的检测结果。而本文的方法中,分形维数和自相关函数绝对值均值两个因素受噪声的影响都相对较小,各自的特性不曾发生明显改变,所以在二者的相互作用下,依旧能获得较为准确的检测结果。
4 结 论
根据语音存在混沌的特性,引入了分形维的概念。根据语音信号和噪声信号自相关函数的区别,引入了自相关函数绝对值均值。通过对语音信号进行分帧预处理,计算各个语音帧的分形维数与自相关函数绝对值均值,然后将分形维数与自相关函数绝对值均值结合起来,基于传统的双门限思想,对分形维数与自相关函数绝对值均值设置合适的阈值,对语音的端点进行检测。实验表明本文方法能够有效避免噪声干扰,准确地判断出语音的起止点,也能判断出语音的清音部分。通过与传统双门限检测方法的对比,展现出基于短时能量与短时过零率的传统双门限检测方法的不足,表明了本文方法的效果优于传统的检测方法。当然本文方法也有许多有待改进的地方。本文不曾对汉语语音进行测试,对于汉语中语音结构复杂的端点检测有待后续进一步深入研究,同时,本文方法未与信号降噪等方法相结合,对于先通过降噪算法进行语音降噪处理然后再采用本文方法判断端点的联合效果也有待进一步研究。
参考文献:
[1] 陈锡锻.一种双门限语音端点检测算法 [J].浙江工贸职业技术学院学报,2021,21(2):43-46.
[2] 沈蓉.智能门禁系统声纹识别中端点检测算法研究 [D].西安:西安科技大学,2015.
[3] 吴边,王忠,刘兴涛.强背景噪声下语音端点检测的算法研究 [J].计算机工程与应用,2011,47(33):137-139.
[4] 薛胜尧.基于改进型双门限语音端点检测算法的研究 [J].电子设计工程,2015,23(4):78-81.
[5] 邓艳容,景新幸,杨海燕,等.语音端点检测研究 [J].计算机系统应用,2012,21(6):240-243.
[6] 朱春利,李昕.基于LMS减噪与改进的双门限语音端点检测方法 [J].系统仿真学报,2017,29(9):1950-1960+1967.
[7] 夏令祥.低信噪比环境下语音端点检测方法的研究 [D].徐州:中国矿业大学,2019.
[8] HAGHANI S K,AHADI S M. Robust voice activity detection using feature combination [C]//2013 21st Iranian Conference on Electrical Engineering (ICEE).Mashhad:IEEE,2013:1-5.
[9] 刘炜杰,安桐,张涛.基于Katz维数的改进谱减算法 [J].信息与控制,2021,50(6):677-684.
[10] 崔东东,张恒璟,程鹏飞.一种自相关函数绝对值均值变点的去噪方法 [J].测绘科学,2019,44(12):42-49.
作者简介:陈航(1998—),男,汉族,湖北孝感人,硕士研究生在读,主要研究方向:数字信号处理;伍子嘉(1997—),男,汉族,江苏扬州人,硕士研究生在读,主要研究方向:机器视觉与深度学习;彭勇(1967—),男,汉族,江苏无锡人,副教授,硕士,主要研究方向:嵌入式软件与设计;宋伟(1981—),湖北恩施人,教授,博士,主要研究方向:机器学习、自然语言处理。
