A comparative study of the self-propelled jumping capabilities of coalesced droplets on RTV surfaces and superhydrophobic surfaces

Sheng-Wu Wang(王晟伍), Lu Peng(彭璐), Jun-Wu Chen(陈俊武), and Lee Li(李黎)

School of Electrical and Electronic Engineering,Huazhong University of Science&Technology,Wuhan 430074,China

Keywords: self-propelled jumping,vulcanized silicon rubber(RTV),superhydrophobicity,self-cleaning

1. Introduction

The self-propelled jumping phenomenon induced by droplets coalescence is considered with distinct engineering application prospects,[1,2]as it helps surfaces to achieve anti-condensation,[3,4]anti-icing,[5,6]and selfcleaning properties.[7,8]Understanding the mechanism of selfpropelled jumping phenomenon is crucial for optimized manufacturing of outdoor functional coatings,for instance,the insulation coatings of electrical power system’s apparatuses,with the above-described properties,to reduce the hazards induced by high humidity,icing,and contamination.

The phenomenon was first observed by Boreyko and Chen in 2009.[9,10]Due to its distinct application potential,the mechanism of self-propelled jumping behavior has been extensively studied through experimental observations,[11,12]numerical analysis,[13,14]and simulations[15,16]and well understood during the past decade. However, so far self-propelled jumping phenomenon has been only observed and studied on the surfaces with superhydrophobicity, which is normally quantified by a water contact angle above 150◦and a contact angle hysteresis value less than 5◦.[17]While neither in laboratory conditions nor in practice, the phenomenon has been observed on the surfaces with weaker hydrophobicity,such as room temperature vulcanized silicon rubber(RTV)coatings.

From the perspective of thermodynamics-based energy conservation,energy surplus is a necessary requirement for the coalesced droplet to jump. Whether the criterion of superhydrophobicity coincidently determines the surface capability of promising energy surplus for coalescence-induced jumping is still unclear.This is of importance,as it poses the question that whether all superhydrophobic surfaces can trigger the jumping of coalesced droplets, or whether all the surfaces without superhydrophobicity cannot be supposed to promote the desired behavior.

In this paper,basing on a numerical prediction model,we found there existing a critical value of apparent contact angle,with which the energy leftover of the coalesced droplet is zero.Moreover,the droplet-size dependent variation characteristics of the kinetic energy magnitudes of coalesced droplets appear to be totally different between the cases with apparent contact angles higher and lower than the critical one.

With respect to the above issues, the energy conversions during the droplets’ coalescence processes on RTV surface and superhydrophobic surface are analyzed quantificationally,the magnitudes of the energy released and dissipated during the coalescence process is calculated through the proposed cluster of equations and then compared,corresponding results demonstrate in detail how the apparent contact angle difference between RTV coatings and superhydrophobic coatings can lead to completely different energy conversion results of the coalesced droplets onside, which lead to different motion behaviors of the coalesced droplets.

2. Numerical model description

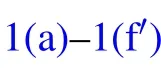
In humid conditions, on superhydrophobic surfaces, the volumes of individual droplets increase due to continuous condensation,adjacent droplets meet and start to merge into each other to achieve minimal surface energy.[18]At the moment the liquid bridge linking the coalescing droplets hits the substrate surface,[19]the horizontal velocity transits into vertical velocity, as being illustrated in Figs. 1(b)–1(d), the apparent contact area between the coalesced droplet and substrate shrinks, meanwhile, the centroid of the merged droplet ascends gradually,[2]when the contact area reduces to zero,the coalesced droplet would be able to jump as long as the vertical velocity at this moment is positive(Figs.1(e)–1(f)).

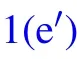
Considering the energy conversions during the processes described above, during the coalescence, the droplets merge into each other to achieve energy minimization, by reducing the total surface area,leading to surface energy surplus.

Fig.1. Schematic diagram of the dynamic behaviors of coalesced droplets on superhydrophobic surface(a)–(f)and RTV surface(a)–(fh).

During the process of droplet coalescing and deformation, the released surface energy ∆Eswould compensate for the internal viscous dissipation ∆Evisof the droplet,the work of adhesion ∆Ehys, the contact angle hysteresis induced energy consumption ∆Ecah,the rise in gravitational potential energy ∆Eh, together with the rise in surface energy ∆Ecoaldue to the shrinking of solid–liquid’s interface area.[2]After being consumed by the energy dissipations described above,the energy surplus ∆Ek0will partially transfer into the kinetic energy triggering droplet jumping. The coalescence process of droplets satisfies the law of energy conservation,the relationship between the energy surplus ∆Ek0and the energy dissipations mentioned above is derived as

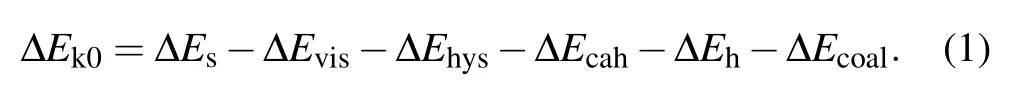
A positive value of ∆Ek0permits the coalesced droplet to jump, in contrary, a non-positive value of ∆Ek0indicates the released surface energy ∆Eswould be totally consumed by those energy dissipations, and cannot support the further motions of the coalesced droplet. In the latter scenario, the coalesced droplet would oscillate at the position it pins, and finally becomes steady after a period of time.[22]

During the coalescence process, the reduction of the solid–liquid contact area is equal to the increase in the gas–solid contact area,the surface energy released during the coalescence process is calculated as[13,23]

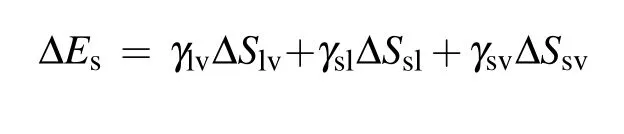
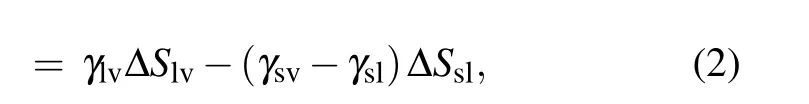
with

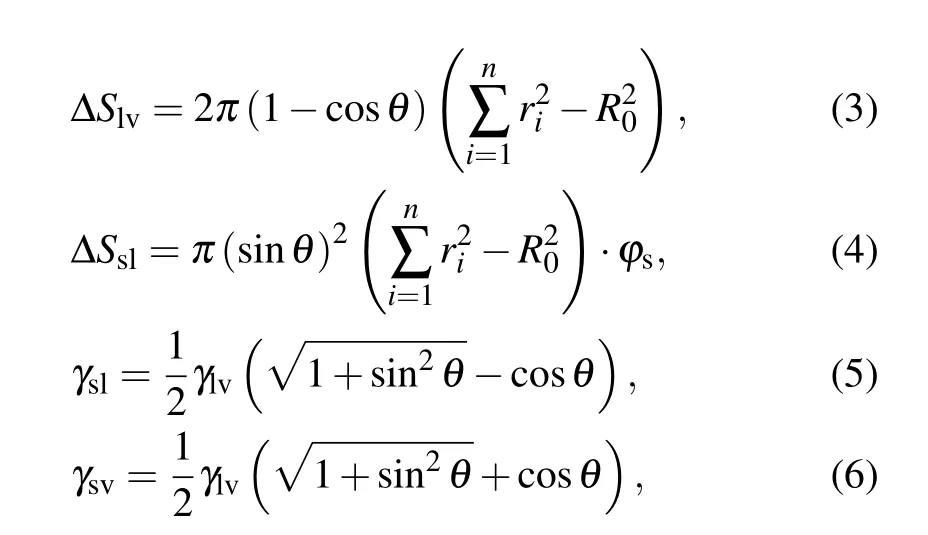
where ∆S is the change in contact area, γ denotes the surface or interface tension, the subscripts s, l, and v represent solid,liquid, and vapor, respectively, ϕsis the fraction of the solid phase contacting the liquid phase, and θ is the apparent contact angle of the liquid.

The internal viscous dissipation within droplets is commonly computed according the following approximate equation:[14]

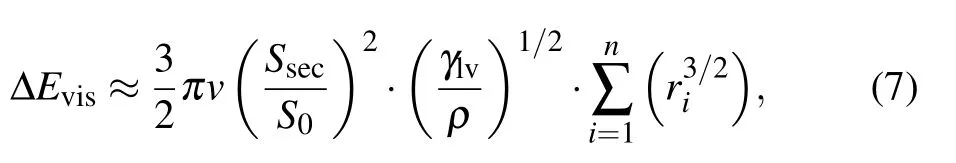
with

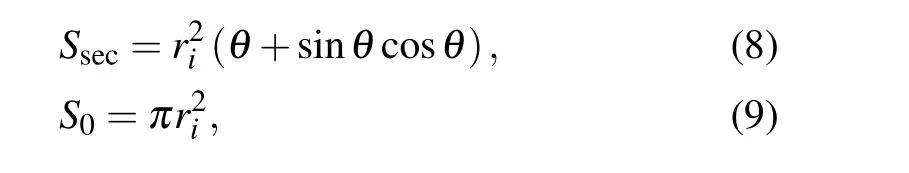
where v is the viscosity of the liquid,and ρ is the liquid density.

During the coalescence process, the work of adhesion∆Ehysis calculated as[14,24]

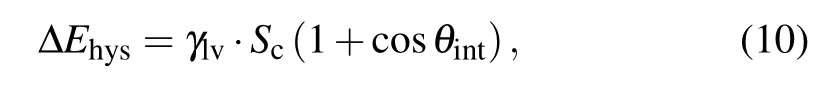
with

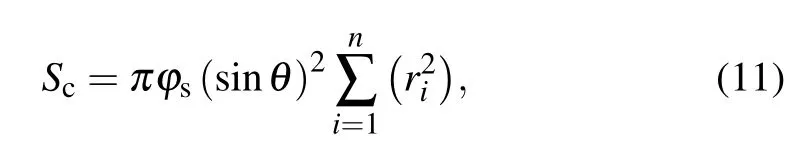
where Scis the total contact area between the pre-coalesced droplet and the substrate surface,and θintdenotes the intrinsic contact angle.

Due to the inherent structural defects and chemical heterogeneity of surfaces, the contact line (which is the outer boundary of the solid–liquid interface)pins to the surface and causes contact angle hysteresis.[25]The energy required for a droplet to move against contact angle hysteresis is calculated by multiplying the hysteresis resistance with the displacement of the contact line[26]

where θais the advancing angle, θris the receding angle, the difference between cosθaand cosθris defined as contact angle hysteresis. k is an empirical coefficient,the value of which is depended on the shape of the three-phase line. In our cases,k=1.27.

The increase in the gravitational potential energy of the coalesced droplet comes from the following two aspects: on the one hand, the centroid of the droplet is raised by the increase in the droplet volume,on the other hand,for the merged droplet to jump, its centroid would be raised to the critical height,in which case the droplet is about to leave the substrate surface(Fig.1(e)).

Considering the shape of droplets on surface to be spherical caps,[27]during the coalescence process, the centroid height of each connected droplets hi,and that of the entire coalescing droplet formed by the connected individual droplets H0could be calculated respectively by[16]

where H0=hiin the case that the coalescing droplets have equal radius.

The critical centroid height of the entire droplet H1at the moment Ssl=0 is calculated as[16]

Hereby the increase in gravitational potential energy at the moment the coalesced droplet is about to leave the surface is calculated as

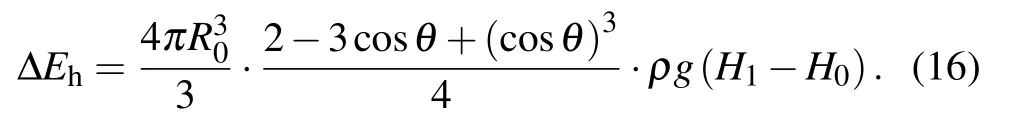
During the procedure indicated as Figs. 1(d)–1(e), the bottom radius of the droplet shrinks due to the inertia force,leading to the reduction of the solid–liquid contact area, as well as the increase in the droplet surface free energy ∆Ecoal,which could be calculated as

After the moment the liquid bridge between coalescing droplets hits the substrate, the direction of kinetic energy converts from horizontal to vertical with efficiency around 25.2%,[2]the kinetic energy ∆Ekthat could drive the droplet to jump is

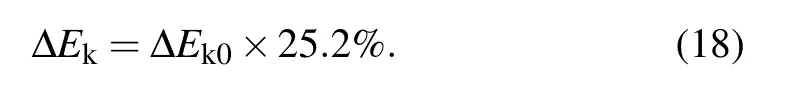
After the moment the droplet is about to jump, the effective kinetic energy of the droplet would completely convert into gravitational potential energy(with the ignorance of air resistance),[2]the initial velocity v0of the pre-bouncing droplet is calculated as

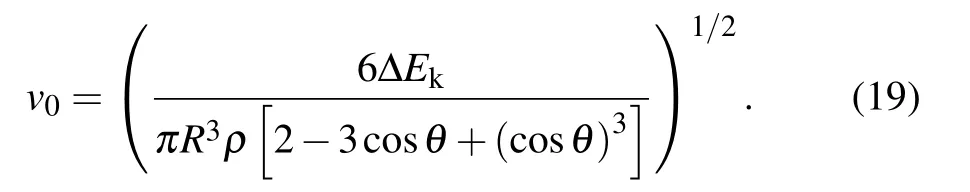
For verifying the accuracy of the theoretical model deduced above,the radius dependent variation curve of the initial jumping velocity v0of the two droplets with the same radius r is shown in Fig.2.

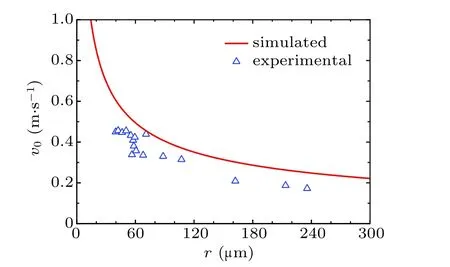
Fig.2. Initial velocities of the droplet coalesced from two individuals with equal radius.

The overall variation trend of the simulated curve aligns with that of the experimentally tested data,the over-prediction can be explained, as having been demonstrated by Chen et al.[28]In practice, during the coalescence process of individual condensates, the moving condensates contacting surfaces with dynamic interfacial areas are larger than the constant values substituted into the numerical equations, therefore inducing larger work of adhesion. Besides,the calculation of ∆Ecahhas assumed that the contact line is circular. While in practice,the profiles of contact lines are more complex,[29]especially on surfaces with microscale roughness, therefore the energy required for contact line moving is larger, resulting in larger value of ∆Ecah.

Apart from the over-prediction, the velocity variation trend in Fig.2 decreases monotonically. While in some works,[2,24]the patterns of obtained velocity variation trends are different,they have an increase at first and afterwards decrease. The discrepancy between the two patterns of variation trends appears in the cases with small radius,as in practice,[28]when the droplet size is smaller than that of micro-scale structures on solid surfaces,they would be trapped within the gaps between the structures and contact the surface with significantly larger area than the theoretical value, causing significant positive deviations in the magnitudes of energy dissipation terms introduced in Eq. (1). As a result, the previously introduced equations can be failed in predicting the velocities of the coalesced droplets under these conditions.

From Fig.2,it could be observed that when droplet radius r is larger than about 60 µm, the simulation result of droplet velocities based on the proposed model agrees well with the previously-reported experimental results.[30]In this paper,we only consider the scenarios with droplet radius no less than this threshold.

3. Analysis of the characteristics of critical apparent contact angle

The existence of effective kinetic energy of the coalesced droplet is a necessary requirement for inducing the jumping behavior. As we have mentioned previously, almost all reported self-propelled jumping phenomena were observed on the superhydrophobic surfaces whose apparent water contact angles are over 150◦. Basing on the previously introduced equations, the magnitudes of kinetic energy ∆Ekin the cases with different combinations of droplet size and surface wettability(quantified by apparent contact angle)are plotted. At the same time,it has been found that the coalescence induced self-propelled jumping capability can be enhanced with more droplets.[31]At the same time,according to Chen et al.,[28]the probability of the coalescence event with more than 4 droplets is small. In this work, whether the coalescence of different number of droplets with equal radius on the surfaces with different wettability would produce the energy surplus required for droplet jumping is investigated.

For a specified kind of liquid (here we choose water for instance) on the different non-wetting surfaces with different apparent contact angles, the values of ∆Ekin the cases with two,three,and four equal-sized droplets are shown in Figs.3,4, and 5, respectively. The abscissas are the apparent water contact angles quantifying the surface wettability,and the ordinates are the radius of the coalesced droplets. The values of droplet size and apparent contact angle can be assumed to be independent,[32]therefore the influence of each parameter on the values of ∆Ekcan be independent as well to that of the other. The vertical dotted lines are the critical value indicators along which the value of ∆Ekis zero. On the left-hand side of the dotted line, ∆Ekhave negative values, indicating there being no energy leftover from the coalescence process.On the right-hand side of the dotted line,the values of ∆Ekare positive,which is the necessary condition for inducing droplet jumping.

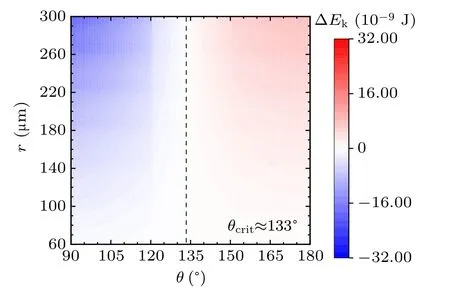
Fig.3. Energy leftover of the droplet coalesced from two equal-radius ones in the cases with different contact angles and radii.

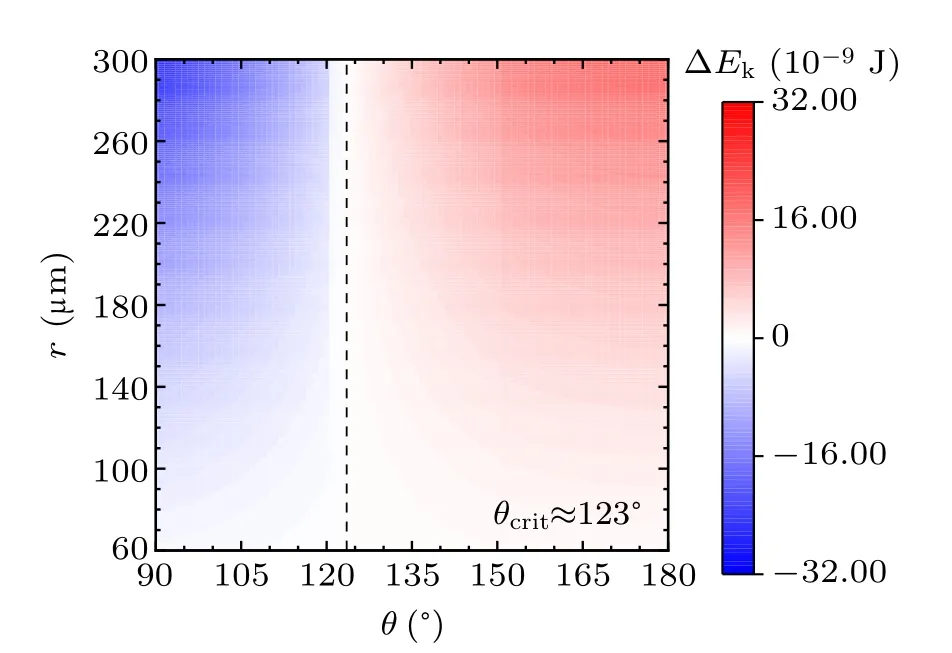
Fig.4. Energy leftover of the droplet coalesced from three equal-radius ones in the cases with different contact angles and radii.

Fig.5. Energy leftover of the droplet coalesced from four equal-radius ones in the cases with different contact angles and radii.

The simulation results in the above figures indicate the critical values of apparent contact angle θcritquantifying surfaces according to their water-repellency into two categories,one of which can promise kinetic energy for the specified kind of coalesced droplet,and the other cannot. For self-propelled jumping being promoted, the apparent water contact angle of surface is required to be higher than θcrit,so that the released surface energy can have surplus after compensating the energy dissipations during the coalescence process, to partially convert into kinetic energy to induce droplet’s jumping. θcritdecreases with the increase of droplets number convergently.

Apart from this, from the figures it can be inferred that on the surfaces with apparent water contact angles(as we used water to be the liquid)larger than θcrit,the increase in droplet size leads to the higher magnitude of ∆Ek. On the contrary,for the surfaces with weaker water-repellency,the increase in droplet size would make ∆Ekeven smaller. From the above description,the variation characteristics of energy conversions on the two kinds of surfaces are completely different.

In practice,the apparent water contact angle on RTV surface is no larger than 120◦,the reason that coalesced droplets on RTV surface are not able to jump can be explained by the theoretical results. Superhydrophobic surfaces support sessile drops with apparent contact angles larger than 150◦, according to the calculated results,the coalesced droplets can be promoted to jump due to the surplus of the released surface energy.

4. Analysis of the energy conversions during the droplet coalescence process on RTV surfaces and superhydrophobic surfaces

In the above section, we have found the contact angle value threshold θcrit,above which there will be kinetic energy leftover after the droplet coalescence process. The threshold categorizes water-repellent surfaces into two categories, between which the radius-dependent variations characteristics of∆Ekare different.

In this section, the difference is analyzed by comparing each kind of energy terms generated and dissipated during the coalescence processes on different surfaces.

4.1. Analysis of the surface energy released during coalescence process

The surface energy released during the coalescence process of droplets is calculated in the cases with different droplet radii. At the same time,the dependency of the energy magnitude on the apparent contact angles,droplet numbers,and size ratios is considered respectively.

Figure 6 shows the droplet radius dependent variation of the surface energy ∆Esreleased from the coalescence process of droplets on RTV surfaces and superhydrophobic surfaces,quantified by different apparent water contact angles. Both on RTV surfaces and superhydrophobic surfaces, the surface energy released is positively related to the value of droplet radius. In the cases with the same droplet radius, ∆Esreleased on superhydrophobic surfaces is larger than that on RTV surfaces,moreover,the larger the apparent water contact angle is,the larger the magnitude of the released surface energy will be.This could be explained by that a larger apparent water contact angle of the coalesced droplet indicates a larger gas–liquid contact area and a smaller liquid–solid contact area,leading to a larger amount of surface energy being released from the coalesced droplet.

Fig.6. Surface energy released during the coalescence of droplet pairs on RTV surfaces and superhydrophobic surfaces (SHP), in the cases with different surface wettability.

The apparent contact angle of a certain liquid droplet on a surface is commonly regarded as the wettability of the surface. The apparent water contact angles on RTV surfaces are normally smaller than 120◦,but on superhydrophobic surfaces are literally larger than 150◦. The water-repellency of RTV coatings leads to the less amount of surface energy ∆Esreleased from the coalescence process.

To further validate the conclusions drawn above,take the RTV surface and the superhydrophobic surface with apparent water contact angles of θ =100◦and θ =160◦respectively for instance, simulate the surface energy released in the scenarios with different numbers of droplets and different ratios of droplet radius,and check the variations of the released surface energy.

Figure 7 shows the droplet radius dependent variations of the surface energy ∆Esreleased from the coalescence process of the droplets with equal radius, in the cases with different droplet numbers and different surfaces. With equal droplet radius, and on the same kind of surface, the released surface energy ∆Esis correlated positively with the numbers of droplets. With equal droplet radius and numbers, ∆Eson superhydrophobic surfaces is larger than that on RTV surfaces.

Figure 8 shows the droplet radius dependent variation of the surface energy ∆Esreleased from the coalescence process of the two droplets with different radii. The values along the horizontal axis are r1,which denotes the radius of the smaller droplet, hence the radius of the larger droplet is r2=r1·k,where k is the radius ratio. The trends indicate that within the considered range of droplet radius, the higher the value of k,the larger the magnitude of ∆Es.

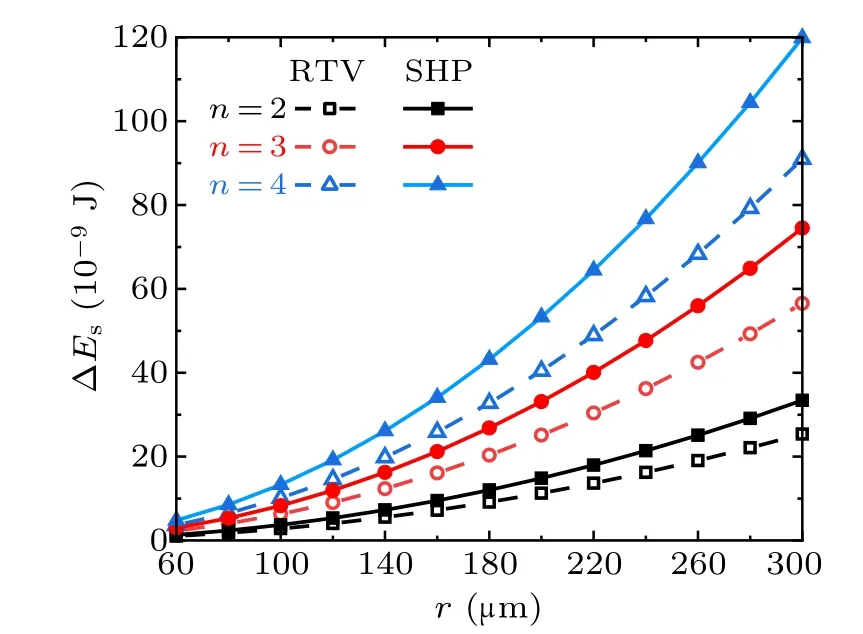
Fig.7. Surface energy released from the coalescence of different numbers of droplets on RTV surfaces and superhydrophobic surfaces(SHP)in the cases with different droplet radii.

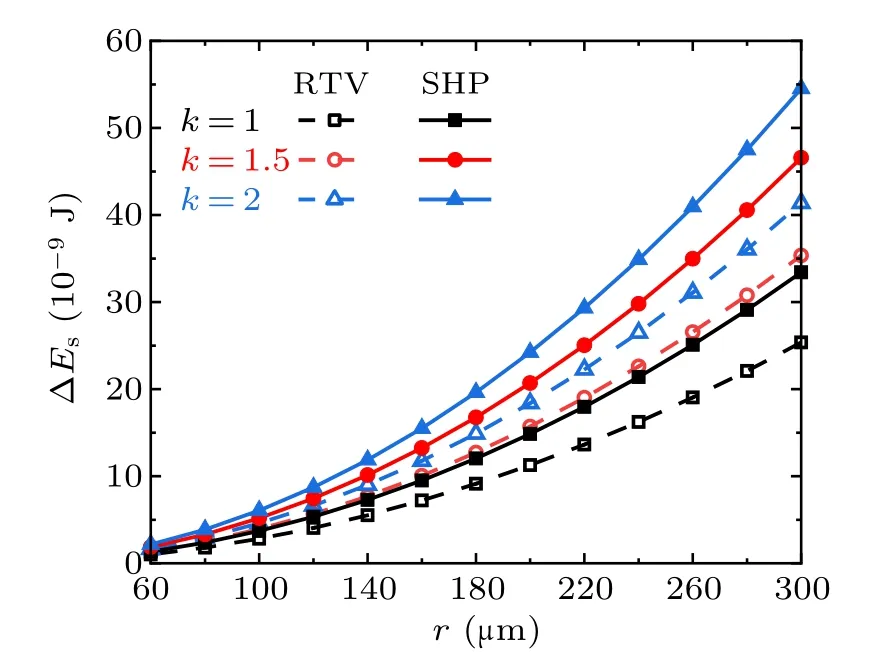
Fig.8. Released surface energy in the cases with different radius ratios on RTV surfaces and superhydrophobic surfaces(SHP).

According to the calculation results, from the perspective of surface wettability, with equal numbers and radius of droplets,the surface energy ∆Esreleased from the coalescence process on super-hydrophobic surfaces is always larger than that on RTV surfaces,no matter how the droplet number or the radius ratio changes within the considered range. On the same surface,∆Esis positively related to the number of droplets and the droplet radius ratios.

4.2. Analysis of the energy dissipations during droplets coalescence process

The surface energy ∆Esreleased during coalescence process would be partially or completely consumed by the various kinds of energy dissipations. Basing on the previously presented equations, the variations of different kinds of energy dissipations during the droplet coalescence process on RTV surfaces and superhydrophobic surfaces are studied.

To analyze the variation characteristics of the energy dissipations during droplets coalescence processes on RTV surfaces,set the water contact angle,advancing angle,and receding angle to be 100◦, 110◦, and 70◦respectively, set ϕs=1,for the coalescence process of two droplets with equal radius,the magnitudes and proportions of each kind of energy dissipations in the cases with droplet radius in the range from 60µm to 300µm are illustrated in Figs.9 and 10,respectively.

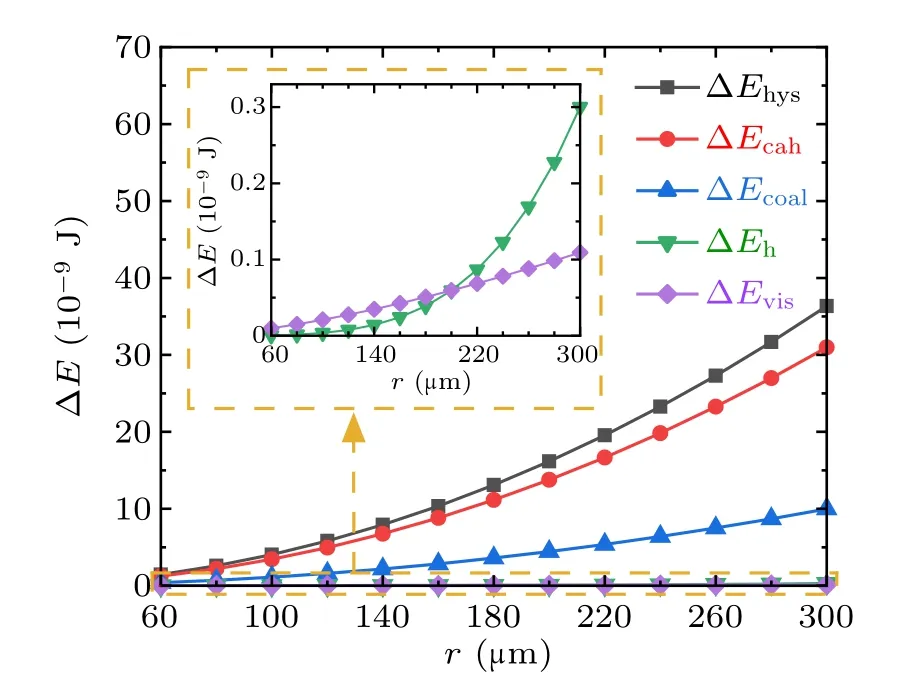
Fig.9. Magnitudes of energy dissipations during the droplets’ coalescence process on RTV surfaces.

From Figs. 9 and 10, during the coalescence process of droplets on RTV surface, the magnitudes of all kinds of energy dissipations increase with the droplet radius. The largest proportion is 70%,taken by ∆Ecahwhich is caused by the contact angle hysteresis,and followed by ∆Ehys,which is around 30%. The proportions taken by ∆Ehand ∆Evisare both less than 0.5%,and therefore negligible.

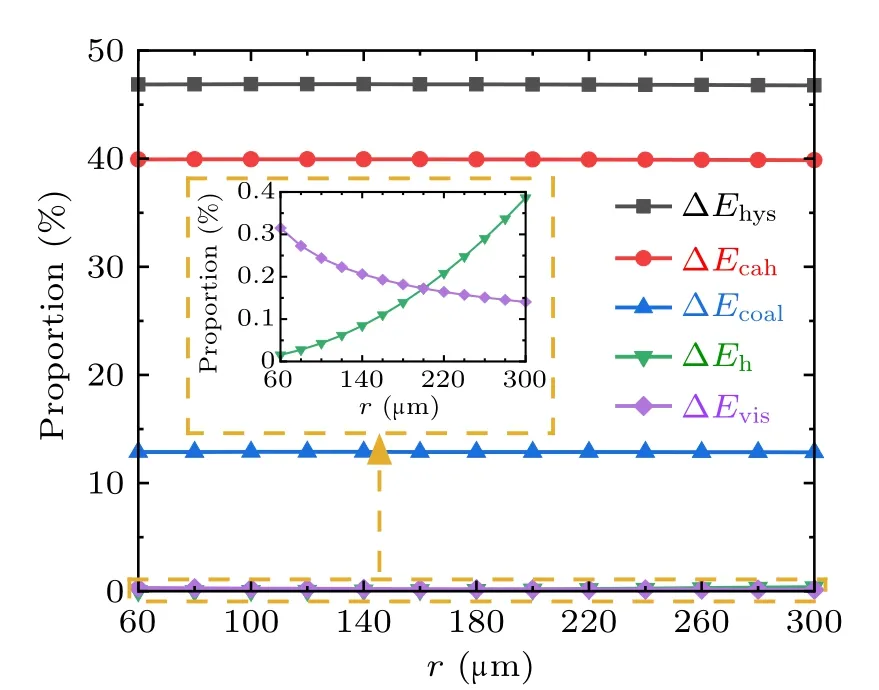
Fig.10. Proportions of each energy dissipation during the droplets’coalescence process on RTV surfaces.

For the cases with superhydrophobic surfaces,set the apparent water contact angle,advancing angle,and receding angle to be 160◦,161◦,158◦,respectively,set ϕs=0.8,for superhydrophobic surface. The magnitudes and the corresponding proportions of each kind of energy dissipations in the cases with different droplet radius within the considered range are illustrated in Figs.11 and 12,respectively.

From Figs. 11 and 12, the major proportion of the energy dissipation during the coalescence process on the superhydrophobic surface is around 70%. taken by ∆Ehys, and the proportions taken by the other energy dissipations are relatively indifferent.

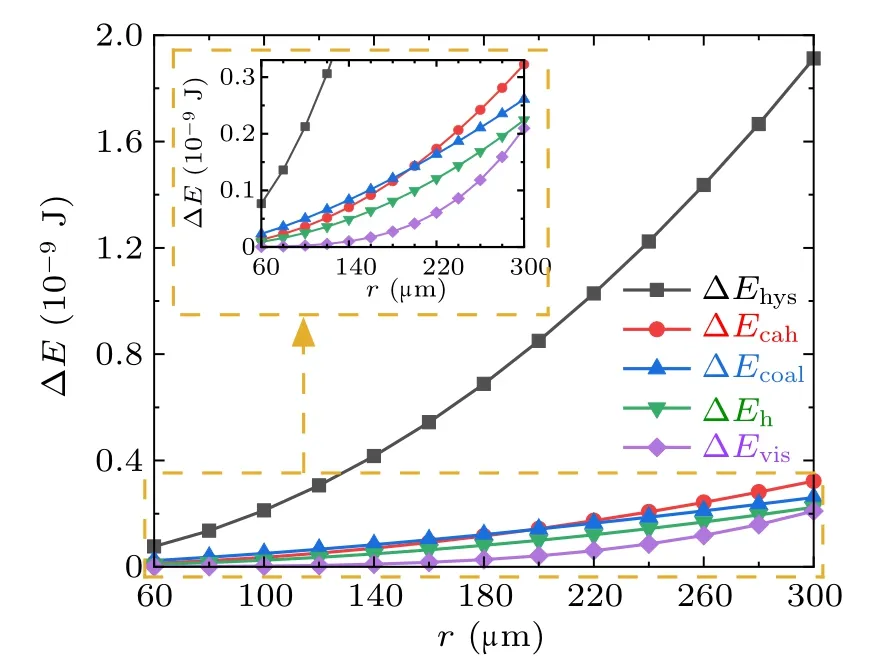
Fig.11. Magnitudes of energy dissipations during the droplets’coalescence process on the superhydrophobic surface.

Fig.12. Proportions of the energy dissipated during the droplets’coalescence process on the superhydrophobic surface.

By comparing the magnitudes and corresponding proportions of energy dissipations during coalescence process on the RTV surfaces and the superhydrophobic surfaces, it is clear that the magnitudes of ∆Ehand ∆Evisare similar,and have little effect on the coalescence process. The difference between droplet motion characteristics on the two kinds of surfaces mainly relates to the magnitudes of ∆Ehys,∆Ecah,and ∆Ecoal,as the three quantities on RTV surface are significantly larger than those on superhydrophobic surface, the released surface energy would be totally exhausted before the droplet could reach the critical jumping position on RTV surfaces. As a result,the thermodynamic condition for droplet jumping cannot be fulfilled,the coalesced droplet cannot be triggered to jump.

The difference between the variation characteristics of∆Ekin the cases with surface wettability weaker and stronger than the critical value,respectively,can be explained by comparing the magnitudes changes of the above considered energies. For the RTV coating with apparent water contact angle of 100◦and the superhydrophobic coating with apparent water contact angle of 160◦, the changes in the magnitude of each energy term before and after increasing droplet radius from 60µm to 300µm are shown in Fig.13.

Fig.13. Differences in the magnitudes of energy terms between the cases with droplet radius being 60µm and 300 µm,respectively. Blue bars are for the case with RTV coating, and red bars are for the case with superhydrophobic coatings(SHP).

For the above specified case, as having been calculated,the critical value of apparent water contact angle θcritis 133◦.In the case with the RTV coating, θ is less than θcrit, and the increase in droplet radius has more influence on the magnitudes of energy dissipations than that of released surface energy. Especially for ∆Ehysand ∆Ecah, from Fig.13, both of their magnitude changes are higher than that of ∆Es. While in the case with the superhydrophobic surface,the magnitude of the released surface energy is more sensitive than those of energy dissipations to the variation of the droplet size.

Here the discrepancy between the kinetic energy variation characteristics can be explained. With the surfaces that cannot guarantee energy surplus for coalesced droplets,the increase in droplet size leads to significant increase in the magnitudes of energy dissipations,but relatively small increase in that of the released surface energy. With the surfaces that can promise energy surplus for droplet jumping, the increase in droplet size leads to larger amount of released surface energy and can cause relatively little increase in the magnitudes of energy dissipations. As a result, droplets coalesced from larger individual condensates would have more kinetic energy.

In practice,considering corona effect and natural contamination, the aged RTV insulation coatings have lower water contact angle and higher contact angle hysteresis values than the values considered in this paper,[33,34]making it harder for the coalesced droplet to have the kinetic energy for further motions. The larger the condensates are,the harder for the dissipations to be fully compensated by the released surface energy on the RTV coating.

5. Conclusions

With respect to the fact that coalescence-induced jumping behavior has only been observed on superhydrophobic surfaces other than the water-repellent surfaces of RTV coatings,we analyzed the energy conversions during the coalescence processes,and further found the reasons for different variation trends of the kinetic energy leftover for the coalesced droplet on the different kinds of surfaces. Details are as follows.

1. From the thermodynamic-based energy conservation perspective, for a specified combination of liquid droplet and solid surface, there exists a critical value of apparent contact angle,which can be affected by the number of individual droplets to be coalesced and can be smaller than the value indicating superhydrophobicity. RTV coatings normally have apparent water contact angles smaller than the critical one,which means it cannot promise kinetic energy leftover for coalesced water droplets,therefore cannot meet the necessary condition for coalescence-induced jumping.

2. The critical apparent contact angle divides waterrepellent surfaces into two categories with respect to their apparent contact angle values. With smaller angles,the theoretical values of coalesced droplets’ kinetic energy are negative and decrease with the increase of the radius of the individual droplets before coalescence. With larger angles, the theoretical values of kinetic energy are positive, and are positively correlates with the radius of individual droplets to be coalesced together.

3. For superhydrophobic surfaces with apparent contact angles larger than the critical one,the surface energy released during the coalescence process is more sensitive to the change in droplet radius. For RTV coatings with apparent contact angles smaller than the critical one, the energy dissipations magnitudes are more sensitive to the change in droplet radius,hence the coalescence of larger droplets indicates there being more energy dissipations to be overcome for coalesced droplet jumping on RTV surfaces.