Ground-state structure and physical properties of YB3 predicted from first-principles calculations∗

Bin-Hua Chu(初斌华), Yuan Zhao(赵元), and De-Hua Wang(王德华)

School of Physics and Opto-Electronic Engineering,Ludong University,Yantai 264025,China

Keywords: first-principles,high pressures,convex hull

1. Introduction

Superhard materials are widely used in industrial applications such as abrasive substance and polishing tools to wearresistant coatings.[1–3]The most well-known superhard materials are diamond and c-BN.At present,the diamond is still the most rigid and the best thermal conducting material.However,over 800◦C, diamond reacts readily with ferrous metals.[4]The hardness of cubic boron nitride(c-BN)is between 32 GPa and 50 GPa.[5]Unfortunately,it has to be synthesized at high pressure and high-temperature condition,which needs tremendous cost. This makes them expensive and rare.[6–9]Recently,we find that intercalating light elements(boron,carbon,nitrogen, or oxygen) into transition metals could be the right way for searching for potential superhard materials. These compounds,with strong directional covalent bonds,can effectively increase the resistance against the plastic deformations in no small extent. As we all know, the crystal structure is the key to solving the mechanical properties of materials. Therefore,researchers strive to explore novel superhard materials. Recently, many transition metal compounds have been studied,such as ReB2, OsB2, RuO2, WN2, and WB4.[10–17]In these borides,boron rich compounds,such as transition metal(TM)tetraborides and TM triborides have attracted a lot of attention.These compounds are expected to have high bulk and shear moduli. Moreover, they usually form the three-dimensional(3D)covalent bond networks,for example,CrB4,WB4,FeB4,MnB4,VB4,MoB4,and HfB4.[18–31]According to the report,the hardness of CrB4is 48 GPa and the hardness of WB4is 43 GPa. These compounds are regarded as superhard materials. Unfortunately, subsequent studies revealed that the WB3and MoB3are more stable than the earlier mentioned WB4and MoB4structures, and they have unique mechanical properties.[32]An idea raises: Will TM triborides with these similar structures be stable? Whether they have better physical properties? In this situation, many TM triborides,such as TaB3, OsB3, TcB3, RuB3, MoB3, ReB3, CrB3, IrB3,HfB3, and ScB3have been explored and discussed in many works.[33–42]In 2014,Zhang et al. predicted two orthorhombic Cmcm and Amm2 structures for ZrB4. The two structures have large shear modulus and high hardness (42.8 GPa for Cmcm and 42.6 GPa for Amm2).[43]They are all potentially superhard materials. A few more years passed, Zhang et al.predicted a novel C2/m phase for ZrB3. The hardness of this phase is up to 42 GPa. The strong covalent bonding contributes to the high hardness for ZrB3.[44]Yttrium is adjacent to the zirconium in the periodic table,so we expect that boronrich yttrium borides may have good physics properties. In previous studies, there are four phases can be experimentally observed(YB2, YB4, YB6, and YB12)in Y–B systems.[45,46]However, the ground state structure of YB3has never been solved theoretically or experimentally up to now. Therefore,exploring the crystal structure of YB3has an essential significance for high boron contents in Y–B systems.

In the present work, the particle swarm optimization(PSO)algorithm for crystal structure prediction is used to explore the crystal structures of YB3. A novel Cmmm structure for YB3has been revealed under ambient conditions by using the CALYPSO crystal structure prediction method.This method has successfully confirmed by experiments. In our work, the Cmmm-YB3structure is energetically preferable to previously predicted WB3-type, ReB3-type, FeB3-type, and TcP3-type structures. The stability of Cmmm-YB3is confirmed through the study of the elastic constants and phonon.Besides,we also explore the formation enthalpy,elastic constants, and bonding properties of Cmmm-YB3by firstprinciple calculations.

2. Computation details

In this work, the PSO methodology on crystal structural prediction has been performed in the CALYPSO. We have searched the potential crystal structures of YB3under ambient conditions containing 1–4 formula units in each simulation cell. CALYPSO has successfully solved the structures of various systems requiring only chemical compositions and specified external conditions.[47–49]The calculations are implemented in the Vienna ab initio simulation package(VASP)code.[50–52]The generalized gradient approximation (GGA)with the projector-augmented wave(PAW)potential is treated as the exchange–correlation functional.[53,54]The energy cutoff 500 eV and appropriate Monkhorst–Pack k meshes are chosen. Monkhorst–Pack k meshes of 3×4×8 for Cmmm phase,8×3×10 for Pmmm phase, 7×7×5 for WB3-type structure,13×13×7 for ReB3-type structure, 8×12×6 for FeB3-type structure, and 2×11×6 for TcP3-type structure. For hexagonal structures, we use Γ-centered grids. The formation enthalpy of YmBnis confirmed by the following equation:∆H=H(YmBn)−mH(Y)−nH(B),in here,the solid α-B12element is considered as the referenced phases.[55]The phonon calculation is carried out in the PHONOPY code.[56,57]The calculated bulk modulus B and shear modulus G is obtained by the strain–stress method. The theoretical Vicker’s hardness is estimated by Chen’s model.[58]

3. Results and discussion

In the present work, a new orthorhombic Cmmm structure is revealed by the CALYPSO crystal structure prediction method. The orthorhombic Cmmm structure includes six YB3f.u. (a=11.598 ˚A,b=7.761 ˚A,c=3.491 ˚A,α =β =γ =90◦) in a unit cell at ambient conditions. The metal Y atoms have the Wyckoff 4i (0, 0.8093,0) and 4g (0.2754, 0,0)sites, and the four B atoms are at the Wyckoff 8q(0.4214,0.8829,0.5),8q(0.3247,0.7144,0.5),4h(0.8806,0,0.5),and 4l(0,0.5,0.7959)sites,respectively. The polyhedral view for the predicted Cmmm structure is presented in Fig.1. We can see that the Cmmm structure can be described as the alternative arrangement by Y atoms and puckered network formed by B atoms,there is an interesting B–Y–B sandwich stacking sequence along the c axis.

For further investigate the stabilities of different YB3phases,we calculated the total energy per formula unit vs volume for these two candidate structures. For comparison, the four possible structures of the known TM compounds: WB3(P63/mmc, No. 194), ReB3(P¯6m2, No. 187), FeB3(P21/m,No.11), and TcP3(Pnma, No.62)are also considered as the potential phase for YB3, and we define them as the WB3-,ReB3-, FeB3-, and TcP3-type structures. The E–V curves of all considered phases of YB3are illustrated in Fig.2. Among these six considered structures, at first, the Pmmm phase has the lowest total energy minimum. However,with the increase of volume, we can see that the predicted Cmmm phase of YB3is lower in energy than the other phases. There is a phase transition process in our calculations. For aiding experimental synthesis in future,we explore the thermodynamic stability of YB3. The predicted Cmmm structure concerning the separate phases is investigated by the reaction route∆H =H(YB3)−H(Y)−3H(B). The Y (space group: Fm-3m)and α-Boron(space group: R-3m)are chosen as the referenced phases. From Fig.3, it can be seen that the Cmmm phase has the negative formation enthalpy at about −2.2 eV at ambient conditions, indicating that the Cmmm phase is thermodynamic stable and can be synthesized by elemental yttrium and boride. As the pressure increases, the stabilities of the Cmmm phase is gradually decreased. When the increasing pressure comes over 31 GPa, the phase transforms from the Cmmm phase to the Pmmm phase, indicating that the Pmmm phase is a high-pressure phase and more energetically stable at high pressure.

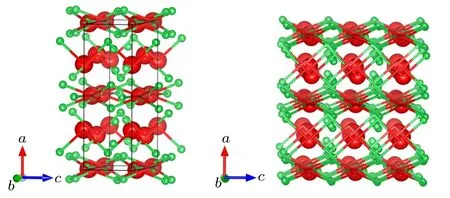
Fig.1. Crystal structure of Cmmm-YB3. Small green spheres represent boron atoms and large red spheres represent yttrium atoms,respectively.

Fig.2. The total energy per f.u. volume for YB3 as a function of volume with six different structures.

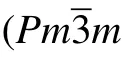
Fig.3. Formation enthalpis versus pressure for different yttrium borides structures.

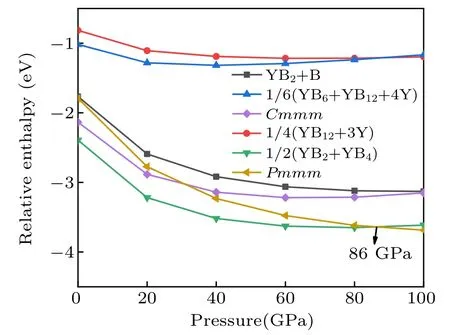
Fig.4.The relative enthalpy–pressure diagrams of the Cmmm-YB3,Pmmm-YB3 and its respective competing phases with respect to elemental Y and B.The α-B(0 GPa–19 GPa),γ-B(19 GPa–89 GPa),and α-Ga phase(89 GPa–100 GPa)were used in the calculations.

To further verify the stability of the Cmmm and Pmmm structures,we present the convex hull plots. We know that all the structures lie on a convex hull could be seen as thermodynamically stable and composable in theory. From Fig.4,the stability of the predicted Pmmm phase is superior to the competing phase YB2+YB4above 86 GPa,so we calculate the convex hull under the pressure of 100 GPa. The convex hull plots of the Y–B system at the selected pressures are depicted in Fig.5. From the convex hull in Fig.5(a), all enthalpies of formation of these compounds are negative, and four stable stoichiometry(YB2,YB4,YB6,and YB12)appear in our convex hull plots. Our proposed Cmmm-YB3is located above the curve of the convex hull,suggesting it is unstable and is going to decompose. Furthermore,from Fig.5(b),the Pmmm structure exactly sits on the curves of the convex hull,indicating it is stable and will not decompose.

Fig.5. The convex hulls of YB3 at the pressure of(a)0 GPa and(b)100 GPa.

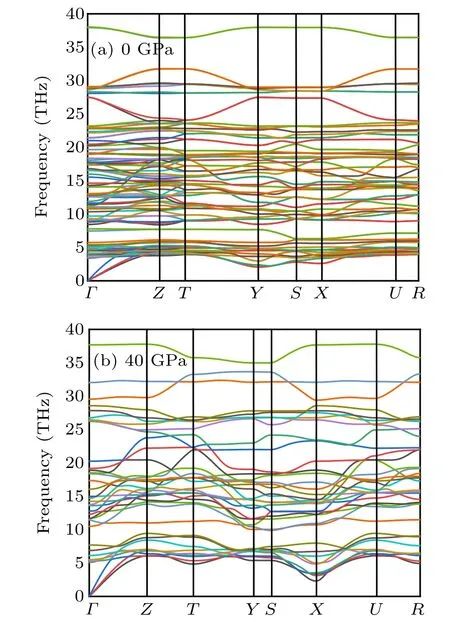
Fig.6. The phonon-dispersion curves. (a) Cmmm phase at 0 GPa, and (b)Pmmm phase at 40 GPa,respectively.

To obtain a deep insight into the dynamical stabilities of the two considered structures,we calculated their phonon dispersion curves. As shown in Fig.6(a),there are no imaginary phonon frequencies in the whole Brillouin zone for Cmmm structure indicates that it is dynamically stable at ambient conditions. From Fig.6(b), there is no soft mode at any vectors in the whole Brillouin zone,suggesting the stability of Pmmm structure at 40 GPa. Besides,the vibrational bands of the optical part into higher frequencies at high pressure.

To further confirm the stabilization of the Cmmm structure,we studied its mechanical stabilities. Mechanical stability plays a crucial role in the stabilization of a crystal.The mechanical properties can also provide beneficial information for the stability and stiffness for materials. The elastic constants were obtained by fitting the stress of the strained structure and the strains. For an orthorhombic crystal, the elastic stability criteria are displayed as follows:

C11>0,C22>0,C33>0, C44>0,C55>0,C66>0,

[C11+C22+C33+2(C12+C13+C23)]>0,

(C11+C22−2C12)>0,

(C11+C33−2C13)>0,

(C22+C33−2C23)>0.

All the elastic constants of the Cmmm structure and Pmmm structure were calculated in comparison with the other transition metal triborides TMB3(TM=W, Cr, Os, and Ta)as seen in Table 1. As shown in Table 1, it is clear that the Cmmm structure satisfies these criteria, indicating that it is mechanically stable at zero pressure. So the Cmmm structure is both mechanically and dynamically stable at ambient conditions. The bulk modulus B and shear modulus G is calculated by using the elastic constants. Besides, Young’s modulus Y and Poisson’s ratio υ are obtained by the equations Y =(9BG)/(3B+G) and υ =(3B−2G)/(6B+2G).As seen in Table 1,the calculated C22for the Cmmm structure is bigger than C11and C33,indicating that the resistance to deformation along the b direction is stronger than that along a and c directions. Besides,the Cmmm structure has a G value of 132 GPa, so it is supposed that this structure can endure the shearing strain to a great extend. Young’s modulus can reflect the stiffness of materials. In Table 1,the Young’s modulus of the six structures exhibit a sequence of WB3>CrB3>OsB3> TaB3> Cmmm > Pmmm. As a result, a structure with a high Y value has a greater stiffness than a structure with a low Y value. Besides, the value of Poisson’s ratio (υ) can be used to describe the degree of directionality of the covalent bonding. From Table 1, we can be seen that all the υ value is below 0.33. Besides,the Cmmm structure has similar Poisson’s ratio to that of CrB3. The ratio value of B/G is a criterion to describe the ductility or brittleness of materials. A B/G value higher(or lower)than 1.75 is considered to be ductile(or brittle).[60]From Table 1,except TaB3,the B/G values of the other phases are under the critical value,implying their brittle nature. The Vickers hardness is calculated by using the Chen’s formula Hv=2(K2G)0.585−3,in which G denotes the shear modulus and K=G/B, respectively. According to this formula, the hardness value of the Cmmm structure is calculated to be 23.8 GPa at ambient conditions. This suggests that the Cmmm structure is a potentially hard material.

Table 1. Calculated elastic constants(in unit GPa),bulk modulus B(in unit GPa),shear modulus G(in unit GPa),Young’s modulus Y (in unit GPa),Poisson’s ratio υ,and B/G ratio of the Cmmm phase,Pmmm phase,WB3,CrB3,OsB3,and TaB3.

To understand the bonding mechanism and origin of materials’ physical properties, the electronic properties of the Cmmm and Pmmm phase were investigated by analyzing their total and partial density of states. From Fig.7(a),we can see that the Cmmm phase exhibits metallic character, with the finite value of the DOS at the Fermi level. Y-4d and B-2p electrons occupy the major orbital,which is the leading cause for the metallicity.Moreover,there is no clear overlap of yttrium’s d electron and boron’s p electron in the range of −11 eV and 5 eV.From Fig.7(b),we can also see that the Pmmm phase exhibits metallic character. Meanwhile, for the two phases, the Y-4d states and B-2p states contribute to most of DOS, and the B-2s states are mainly situated at the bottom of the valence bands.

To gain more in-depth insight into the bonding character of the predicted Cmmm structure,we calculated the electronic localization function(ELF).The electronic localization function(ELF)is widely used to describe chemical bonding. The ELF is a contour chart with the value from 0 to 1. Generally,ELF=1 suggests the entire localization property, ELF=0.5 offers homogeneous free-electron gas, and ELF=0 suggests perfect delocalization. It is worthwhile to note that the bonding type of materials (metallic, covalent, and ionic bonding)can be determined based on the ELF.We plot the contours of ELF=0.75 and(001)plane for the Cmmm structure.As shown in Fig.8,there is the existence of a strong covalent B–B bonding in the Cmmm structure. Therefore, the strong covalent interaction between B–B bonds is the primary reason for its high hardness and stability.

Fig.7. Calculated total density of states(DOS)and partial density of states(PDOS)of the Cmmm phase(a),and Pmmm phase(b).

Fig.8. The contours of the electronic localisation function (ELF) of the Cmmm phase on the(001)planes.

4. Conclusions

In summary, the calypso algorithm with first-principles calculations discovers two stable phases: one ground-state Cmmm-YB3and a high-pressure Pmmm-YB3. These two phases are dynamically and elastically stable. The estimated Vickers hardness values are 23.8 GPa for the Cmmm phase at ambient conditions. This means that the Cmmm structure is a potentially low compressible and rigid material. Analysis of chemical bonding indicates that there are strong covalent and directional B–B bonds in Cmmm-YB3. As we have updated the phase diagram of the Y–B system, we aim to stimulate a further experimental realization of boron-rich transition metal borides through our present theoretical investigation.