卫星通信下行链路鲁棒安全波束成形设计

顾晨伟, 林 志, 林 敏，*, 解路瑶, 欧阳键, 黄 硕

(1. 南京邮电大学通信与信息工程学院, 江苏 南京 210003;2. 国防科技大学电子对抗学院, 安徽 合肥 230037;3. 上海航天电子通讯设备研究所, 上海 201109)

0 引 言

众所周知,多波束天线技术在当前的卫星通信领域得到了广泛的研究和应用,通过对多个点波束进行联合处理,在扩大卫星通信覆盖范围的同时,还能有效地提高卫星通信系统的频谱效率与通信容量[1-2]。然而,由于卫星通信的广域覆盖特性和无线信道的广播特性,卫星发送至合法用户的私密信息很容易被窃听者窃取。据报道,2014年6月一名英国黑客入侵并窃取了美国国防部卫星通信系统中超过800个用户的详细信息,随后还将这些信息在网上传播,美国国防部声称此次黑客事件造成了重大的损失。由此可见,信息安全问题成为了当前卫星通信领域亟待解决的关键问题之一[3-4]。卫星通信系统的安全传输主要依赖传输上层的加密技术得以实现,但是随着计算机技术的发展,尤其是量子计算技术的出现,基于复杂计算的传统加密技术面临着严峻的挑战。在这种情况下,迫切需要探索新的卫星通信安全技术。

近几年来,基于信息论的物理层安全(physical layer security, PLS)技术成为了无线通信领域的研究热点[5-7]。PLS的基本概念首先由Wyner提出,在文献[8]中定义了窃听信道,并构造了窃听信道的数学模型。文献[9]指出当合法用户信道容量大于窃听信道容量,即安全容量大于零时,合法用户的通信是安全的。目前,国内外有关地面通信物理层安全技术的文献比较多[10-11]。与此同时,也有一些文献对卫星通信的物理层安全技术进行了研究,例如文献[12]将PLS技术应用到多波束卫星通信系统的下行链路中,构建了一套针对卫星通信系统的安全性能评价指标,并对构建的指标进行了定性和定量的分析。文献[13]针对存在单个窃听者的多波束卫星通信系统的下行链路,以最大化安全和速率为优化目标,提出了迫零和增强信漏噪比两种安全波束成形(beamforming, BF)算法。文献[14]又将其扩展到了存在多个窃听者的多波束卫星通信系统中,以卫星发射功率为约束,建立了以安全和速率最大化为准则的优化问题,并在此基础上设计了两种安全BF算法。文献[15]研究了基于网络编码的多波束卫星安全通信方法,使用半正定规划(semi-definite programming, SDP)和一维搜索得到了最优BF权矢量,最大程度地提高了多波束卫星通信系统的安全速率。除此以外,还有文献研究了星地融合网络的安全通信,例如,文献[16]分别针对认知星地融合网络中存在单个窃听者和多个窃听者的两种不同情况,在地面用户信息传输速率与卫星用户安全速率满足约束的条件下,以卫星和地面基站总发射功率最小化为优化目标,提出了两种联合BF算法。

虽然文献[12-16]验证了将PLS技术应用到卫星通信中,能够使卫星通信系统具有更好的安全性能,但窃听者通常不是网内用户,假设准确已知窃听者信道状态信息(channel state information,CSI),对于卫星而言不太实际[17]。因此,本文针对存在多个窃听者并且仅知道窃听者大概位置的多波束卫星通信系统,分别以安全速率与安全能效为优化目标提出了两种鲁棒安全BF方案。一是基于系统安全速率最大化准则,在卫星总发射功率受到约束的条件下建立了优化问题,通过将问题转换为广义瑞利商的形式,推导出了最优BF权矢量;二是基于系统安全能效最大化准则,在系统安全速率和卫星总发射功率受到约束的条件下建立了优化问题。由于优化问题中的目标函数为非凸的分式形式,因此本文将其转换成等效的凸差规划形式,然后利用罚函数法和凹凸过程方法将原始问题转换为凸问题,接着提出了一种嵌套迭代算法计算出BF权矢量。最后仿真验证表明,本文所提出的鲁棒BF方案相比非鲁棒BF方案具有更好的安全性能。

1 系统模型

如图1所示,本文研究工作在Ka频段的多波束卫星下行传输系统。该系统由一个静止轨道(geosynchronous equatorial orbit, GEO)多波束通信卫星,一个合法用户和K个窃听者组成。其中多波束卫星采用多馈源单反射面形式的天线,配置有L个馈源产生N个波束(K+1≤N≤L)。合法用户和窃听者均使用高增益的抛物面天线以补偿自由空间损耗带来的影响。在多波束卫星向地面合法用户发送信号时,位于卫星覆盖区域内的K个窃听者采取合作窃听的方式试图窃听卫星发送的信号。

图1 系统模型

在多波束卫星通信系统中,通常采用BF技术来提升系统的性能[18]。假设卫星向合法用户发射的信号为x(t),满足E[|x(t)|2]=1,那么通过卫星BF权矢量w∈CN×1处理后,星载天线的发送信号为wx(t)。该信号经过卫星信道后,合法用户接收的信号和第k个窃听者接收的信号可以分别表示为

(1)

(2)

式中,{hu,hk}∈CN×1分别表示卫星与合法用户,以及卫星与第k个窃听者之间的信道矢量;nu,nk分别表示合法用户和窃听者的加性高斯白噪声,噪声功率可表示为σi=κTiBi,i∈{u,k},其中κ≈1.38×10-23J/K表示玻尔兹曼常数;T为噪声温度;B为噪声带宽。由式(1)和式(2)可以得到合法用户和第k个窃听者处的输出信噪比分别为

(3)

(4)

本文假设K个窃听者采取合作窃听的方式对卫星发送的信号进行合作窃听,卫星通信系统的可达安全速率[19]可表示为

(5)

式中,[a]+=max(0,a)。

当卫星向合法用户传输数据时,不仅发射信号需要消耗能量,并且卫星内部电路也会产生能量损耗,所以卫星通信系统的总功耗为

Ptot=PT+Pc

(6)

式中,PT表示卫星的发射功率;Pc表示卫星发射端的电路功耗。

安全能效定义为安全速率与卫星总功耗的比值[20],可以表示为

(7)

在现有的GEO多波束卫星通信系统中,通常采用Ka频段实现宽带传输。在这种情况下,考虑地面用户天线增益、雨衰、卫星多波束增益和路径损耗等因素的影响,卫星与第m个地面用户之间的下行链路信道矢量可建模为

(8)

(9)

式中,Gmax表示抛物面天线的最大增益;θm为信号到达方向与第m个用户天线主轴方向之间的夹角。式中,bm=[bm,1,bm,2,…,bm,N]T表示波束增益[22],其中的元素为

(10)

(11)

式中,c表示光速;fc表示载波频率;dm,n表示第m个地面用户到第n个卫星波束的距离。

在实际的卫星通信系统中,卫星获得的窃听信道的信道状态信息往往存在误差,窃听者的理想信道状态信息难以获取。因此,本文假设卫星仅已知窃听者的大概位置,窃听者位于不确定坐标区域内,第k个窃听者信道的不确定模型可以表示为

k∈{1,2，…,K}

(12)

式中,xk,L和xk,U分别为第k个窃听者位置坐标x轴的下界与上界,yk,L和yk,U分别为第k个窃听者位置坐标y轴的下界与上界。

2 安全速率最大化准则下的鲁棒BF方案

为了保证卫星与合法用户通信的安全性,本小节研究系统安全速率最大化为准则,同时考虑卫星发射功率受限作为约束条件。该优化问题在数学上可表示为

(13)

(14)

(15)

式中,

k∈{1,2，…,K}

(16)

由于log2(·)函数的单调递增特性,最大化问题可以转换为

(17)

为了便于求解,根据文献[24],基于位置误差的窃听信道可表示为

(18)

式中,μk,i为加权系数;Hk,i为Λk中的第i个离散元素;Mk表示样本个数。

命题1Hk∈Λk的目标函数与Hk∈Ψk的目标函数等价,即

(19)

由此,可得

(20)

同时,可以对wHHkw,∀Hk∈Ψk进行分解:

wHHkw=

wH(μk,1Hk,1,μk,2Hk,2+…+μk,MkHk,Mk)w=

μk,1wHHk,1w+μk,2wHHk，2w+…+μk,MkwHHk,Mkw

(21)

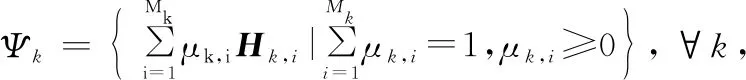
(22)

此时满足

(23)

综合以上,可得

(24)

证毕

命题2式(19)中等式右边的max-min问题与min-max问题等价,即

(25)

证明首先,定义函数ξ(w,Hk):

ξ(w,Hk)=

(26)

∀W,∀Hk∈Ψk

(27)

参考文献[26]中的max-min问题中鞍点的性质,可得

(28)

(29)

将式(29)中的W转换成w,可得

(30)

证毕

根据上述命题1和命题2,式(17)便可改为

(31)

(32)

Rs=

(33)

此时BF权矢量为

w=

(34)

式中,λmax(A,B)表示矩阵B-1A的最大特征值;eig(A,B)表示矩阵B-1A最大特征值对应的归一化特征向量。

进一步,通过使用柯西-施瓦兹(Cauchy-Schwarz)不等式,可得

(35)

因此,为了保证系统的鲁棒性,μk,i的取值应为

(36)

(37)

此时的最优BF权矢量为

w*=

(38)

至此,得到了安全速率最大化准则下的最优BF权矢量的解析解。从推导可知,本方案具有较低的计算复杂度。

3 安全能效最大化准则下的鲁棒BF方案

在第2节中,将安全速率作为优化目标,得到最优BF权矢量。考虑到安全能效作为一个同时衡量安全速率与功率消耗的重要指标,本节将系统安全速率和卫星的发射功率作为约束条件,研究安全能效最大化问题,在数学上建立优化问题:

(39)

(40)

(41a)

(41b)

(41c)

(41d)

rank(W)=1

(41e)

将式(18)中的窃听信道模型代入约束条件中,可以等价改写为

(42)

参考式(36),可以得到μk,i的最优取值。

显然,式(41)为非凸的,为了将其转换为凸问题,引入命题3。

命题3令η*为最大安全效率,那么当且仅当φ(η*)=0时,式(41)与下述问题等价:

log2β-η(tr(W)+Pc)

s.t.式(41c)～式(41e),式(42)

(43)

(44)

(45)

(46)

(47)

(48)

可以进一步转换为

(49)

证毕

同时,由于约束条件rank(W)=1与tr(W)=λmax(W)等价,通过引入惩罚因子ζ,式(43)可以改写为

η(tr(W)+Pc)-ζ(tr(W)-λmax(W))

s.t. 式(41c)～式(41d),式(42)

(50)

式中,log2(·)为凹函数;λmax(·)表示矩阵的最大特征值,是一个凸函数,因此目标函数非凸,将式(50)转化成凸差规划问题来求解:

ζtr(W)-(log2β-ζλmax(W))

s.t.式(41c)～式(41d),式(42)

(51)

ζtr(W);g(W,β)=log2β-ζλmax(W)。依据凹凸过程方法的概念,在第i次迭代过程中,用g(W,Wi,β,βi)作为估计值去逼近函数g(W,β),式中g(W,Wi,β,βi)是g(W,β)在点(Wi,βi)附近的一阶泰勒展开,同时,考虑到g(W,β)为凹函数,可得

g(W,β)≤g(W,Wi,β,βi)=g(Wi,βi)+

(52)

由此可以将式(51)改写为

s.t.式(41c)～式(41d),式(42)

(53)

算法 1 迭代算法

4 计算机仿真

本节将通过仿真验证本文所提的两种鲁棒BF方案的有效性,并引入了非鲁棒BF方案进行对比。假设地面合法用户的坐标位置(x,y)已知为(0 km,0 km)。同时,假设存在两个仅知道坐标范围的窃听者,第1个窃听者位于坐标范围为{(x,y)|150≤x≤300,350≤y≤500}(km)的地面区域内,第2个窃听者位于坐标范围为{(x,y)|150≤x≤300,-500≤y≤-350}(km)的地面区域内。仿真用到的主要参数如表1所示。

表1 主要参数

如图2和图3所示的归一化方向图显示了当卫星波束数为7时,使用安全能效最大化方案得到的BF权矢量进行BF后,合法用户与窃听者的接收信号增益。

图2 归一化三维方向图

图3 归一化俯视方向图

可以看出,使用该方案得到的BF权矢量的最大方向指向合法用户,并将两个窃听者在不确定的区域内的接收信号增益都限制在了-30 dB以下,有效地抑制了潜在的窃听行为,验证了本文所提出的安全能效最大化方案在获得最大系统安全能效的同时,其安全速率也能够满足限制条件。

图4为系统安全速率随卫星发射功率门限的变化曲线图,将窃听信道CSI理想情况下安全速率随发射功率门限变化曲线作为参考,视为性能的上限，设置卫星波束数为7个。

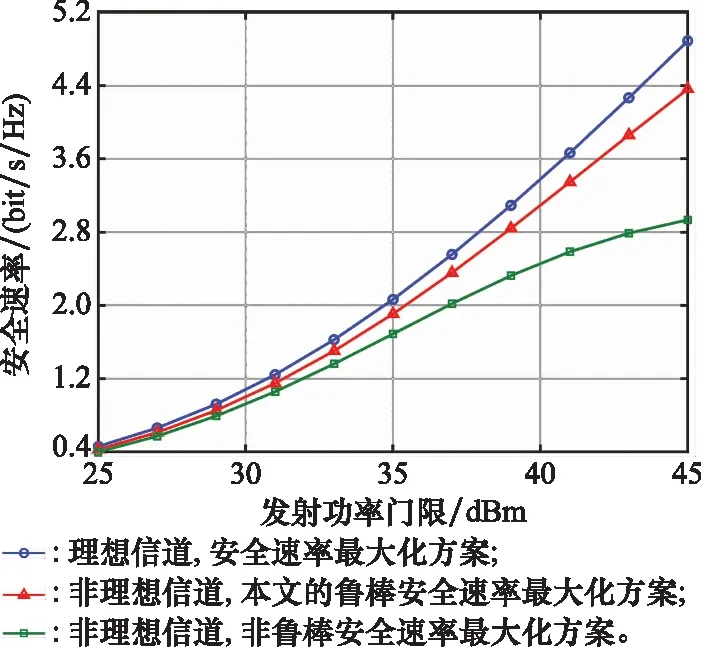
图4 安全速率随发射功率门限变化曲线图

从图4中可以看出安全速率随发射功率的上升而增长。与传统的非鲁棒方案相比,本文的鲁棒最大安全速率方案的求解复杂稍高,但性能更接近窃听信道CSI理想情况下的性能,说明本文所提方案能够更好地抑制不确定区域内窃听者对卫星信号的窃取。图5为系统安全速率与卫星波束数量关系直方图,设置发射功率门限值为40 dBm。

图5 安全速率与卫星波束数量关系直方图

从图5中可以看出,增加卫星波束数能够提高系统安全速率。图6为系统安全能效随发射功率门限的变化曲线图,将窃听信道CSI理想情况下安全能效随发射功率门限变化曲线作为参考,视为性能的上限，设置卫星波束数为7个。

图6 安全能效随发射功率门限变化曲线图

图7为系统安全能效与卫星波束数量关系直方图,设置发射功率门限值为40 dBm。从图7中可以看出,本文提出的鲁棒安全能效最大化方案相比于传统的非鲁棒方案,求解的复杂度稍高,但性能更接近窃听信道CSI理想的情况,因为传统的非鲁棒方案无法抑制不确定区域内窃听者对卫星信号的窃取,从而安全能效较低。同时,增加卫星波束数能够有效地提高系统的安全能效。图8为安全能效与最低要求安全速率门限值的关系曲线图,图9为安全速率与最低要求安全速率门限值关系曲线图。从图8和图9可以看出,存在一个临界的最低要求安全速率门限值,在到达该临界值之前,增大安全速率门限值,系统的安全能效与安全速率均保持不变,并且此时的系统安全速率均等于该临界值。而在到达临界的最低要求安全速率门限值之后,增大安全速率门限值,安全能效减小,因为此时的系统安全速率会随着安全速率门限值的增大而同步增大,这时需要大量提高卫星发射功率来满足不断增加的安全速率要求。从而说明本文所提出的鲁棒安全能效方案能够在最大化系统安全能效的同时,还能在满足最低要求安全速率约束的条件下,最大化系统的安全速率。

图7 安全能效与卫星波束数量关系直方图

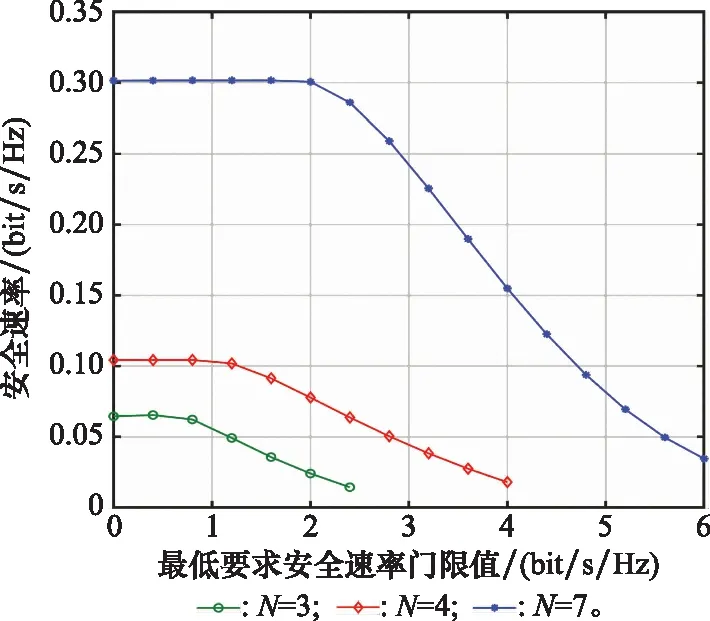
图8 安全能效与最低要求安全速率门限值关系曲线图

图9 安全速率与最低要求安全速率门限值关系曲线图

5 结 论

本文针对存在非理想窃听信道CSI的多波束卫星无线通信系统,基于安全速率和安全能效两种PLS准则分别提出了两种鲁棒BF方案。首先,以卫星发射功率为约束建立安全速率最大化为准则的优化问题,利用广义瑞利商的性质求得BF权矢量的解析解。接着,又以安全速率和卫星发射功率为约束,建立安全能效最大化为准则的优化问题,考虑到目标函数为分式形式,所提出的优化问题非凸,通过将目标函数转换成等效的减法形式,并且引入罚函数法和凹凸过程方法将优化问题转换成凸问题求解。计算机仿真结果显示,本文所提出的两种鲁棒BF方案都要优于相应的非鲁棒BF方案。与基于安全速率准则的方案相比,基于安全能效准则的方案在较大发射功率时能够更好地获得安全性与功耗间的平衡,而基于安全速率准则的方案得益于较低的求解复杂度,适合应用于发射功率较小的场景。两种方案均可以通过增加卫星波束数或者适当地提高卫星的发射功率来提升系统的安全性能。