启发式前后向链条优化组合在轨多目标观测规划算法

张晟宇, 孙煜坤, 朱振才, 胡海鹰

(1. 中国科学院微小卫星创新研究院, 上海 201203; 2. 上海微小卫星工程中心, 上海 201203;3. 中国科学院大学, 北京 100039)

0 引 言

随着敏捷卫星的发展,其姿态机动能力逐步增强,面对突发事件可以通过快速姿态机动完成特定区域指向,以及对多个待观测点的快速切换[1-4]。卫星在轨可以通过接收其他卫星或者地面注入的先验引导信息来完成事件驱动的在轨任务实时响应[5-6]。如在山火蔓延时,大幅宽卫星可以获得多个疑似火点,并将火点信息传输到后方敏捷卫星,引导其进行详查。敏捷卫星一般视场较小,若火点较多,想要在一次过境过程中对多个火点开展有效探测,Liu[7]提出了任务合并的方法，同时需要在轨实时开展观测序列任务规划[8-10],并充分合理地调度卫星姿态机动等资源实现较高观测收益[11-12]。敏捷遥感卫星姿态机动能力提升后,面临着在轨自主能力不足,无法充分利用姿态机动能力提升观测能力的问题。高效自主快速的任务规划方法[13-15],能有效地提升敏捷遥感卫星在轨资源利用效率,增强在轨应用能力。

现在的敏捷卫星具备俯仰、滚动两个维度的机动能力。在轨接收应急任务时,一次过境有限时间窗口内可以对多个点目标进行观测。在轨任务规划应具备:① 实时响应能力,规划求解方法应在较短时间内获得满足任务要求的规划结果;② 充分利用卫星姿态机动能力达到观测效益最大化。

敏捷成像卫星任务规划问题是NP难问题,难以求解。任务规划问题的指数爆炸特征十分明显。贺仁杰[16]总结了主要的遥感卫星规划模型及动态规划、树搜索、智能优化、贪婪算法等主要的求解算法,分析了任务规划求解的特点。其结论是难以建立通用的遥感卫星规划模型,具体问题需要专门的模型及求解方法。

在规划算法的实时响应能力方面。陈书剑[17]针对应急规划问题提出了由自适应免疫算法(adaptive immune algorithm, AIA)和前向动态规划算法(forward dynamic programming algorithm, FDPA)相结合的分解优化策略进行求解的方法,获得了较好的时间响应特性,但总体耗时依然较长。孙凯[18]提出了一种基于专家知识的多种启发式规则,以一种前瞻启发式算法(look-ahead algorithm,LA)在较短的时间内获得局部效果最优的规划效果,但该算法主要解决超过1天的长周期规划任务序列排序问题,时间响应程度不高。伍国威[19]提出了一种面向在轨实时引导成像的多星自主任务规划方法,可实时地通过高收益目标替代低收益目标的方式提高整个规划方案的成像收益,但该方法主要解决多目标向多星系统的分配问题,没有考虑对于单个卫星姿态机动能力的充分挖掘。姜维[20]提出算法协同进化模型求解技术,引入启发式信息的遗传禁忌求解算法,但是同样存在求解时间较长,规划目标数量较少的问题。

在充分利用星上资源方面。Han[21]建立了一个敏捷卫星观测多目标(点目标)的物理模型,基于任务收益的评价和能源及姿态机动的约束,提出基因算法进行观测序列求解的方法,获得了较好的收益效果,但可规划的目标数量较少,同时是以较少的能源消耗作为优化方向的。Mok[22]针对两个自由度机动能力的卫星,开展对于多个点目标的观测序列规划,其主要方法是通过将待观测目标分类、选择,并设计一种基于优先级的任务评价函数结合所有观测时间窗口的冲突消解来进行观测序列规划与优化,由于需要计算所有潜在的窗口并多次迭代,算法只能适应不超过10个目标的观测序列规划,不适用数量较大的目标规划。张科科[23]也提出过在分布式卫星任务规划中将待规划目标编成序列的方法,也未考虑充分发挥卫星机动能力的设计。何磊[24]在提出的云层遮挡时间窗口的计算方法中增加了预判和二分法推进环节,有效提高了算法的求解效率,但主要是针对无云窗口的组合问题求解。陈金勇[25]构建了多星协同任务规划组合优化模型,并且建立超启发式算法求解问题框架,具有一定的面向资源利用模型设计上的启发性,但主要开展的是多种智能算法的比较,不具备问题针对性。Guo[26]提出了面向姿态、数传等资源约束的在轨应急求解算法,具有较好的星上可实现性,但只解决了星上不同任务模式的排序组合问题。孙立远[27]设计了针对导弹目标的基于动态优先级的启发式算法,能够克服群体智能算法在模型适配性和实时性方面的缺陷,但存在适配目标较少的问题。

结合以上方法的分析可以看出,对于敏捷遥感卫星的任务规划算法的研究体现出了非常明显的问题导向趋势,不同的具体问题需要相对应的任务规划策略,不同的时效性要求和优化效益评估也决定了求解方法的选用。针对在轨一次过境多目标的观测序列规划问题,没有针对性的研究。

本文面向具备两维姿态自由度的敏捷卫星一次过境对100个目标进行观测序列规划,提出一种基于启发式前后链条优化组合的点目标观测路径序列规划算法,结合卫星两维自由度提出了前向链条和后向链条的链条生成策略,再通过链条间组合所产生的姿态机动代价决定链条间的组合选择,并在此过程中有选择地进行链条上目标数量的调整。该算法时效性好,星上计算开销小,有较好的工程可实现性。

1 多目标观测问题描述

1.1 问题描述

本文主要研究敏捷卫星在轨对大量待观测目标进行观测序列规划的问题。典型场景中宽幅载荷获得大范围内多个待观测的点目标的位置信息和优先级,如图1所示。后续飞越的敏捷卫星接收这些点目标的位置信息及状态评估信息,在过境的有效时间内通过在轨规划,充分利用卫星姿态机动能力实现观测收益的最大化。

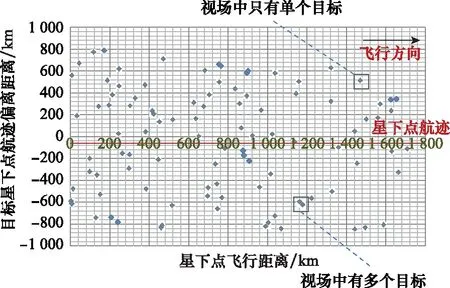
图1 目标沿卫星航迹分布示意图

根据敏捷卫星的机动能力,验证对于目标数量在30～100个之间的观测路径规划能力。目标在分布上应该考虑到其合并情况,即如果两个目标之间的沿迹向与切迹向的距离,小于目标在此观测角度的视场的宽度与长度,则可将2个点目标进行合并,以二者连线的点为指向点后,作为一个目标进行规划。

1.2 任务模型

在该问题中,敏捷卫星的姿态机动能力被定义为具备滚动轴与俯仰轴两轴的自由度。如果只考虑滚动轴一维的姿态机动能力即一维自由度,则卫星飞越待观测区域的过程中主要采取的观测模式只有左右两侧的正侧视观测模式。如图2所示,一旦卫星飞越目标则卫星不具备对目标的观测可能性。二维自由度的目标观测模式下,如图3所示卫星不但具备滚动向的姿态机动能力,同时具备俯仰轴的机动能力,因此卫星具备在未飞达目标时对目标进行前向观测,以及在飞越目标之后对目标进行后向观测的能力,使得卫星拥有更为灵活的观测模式。

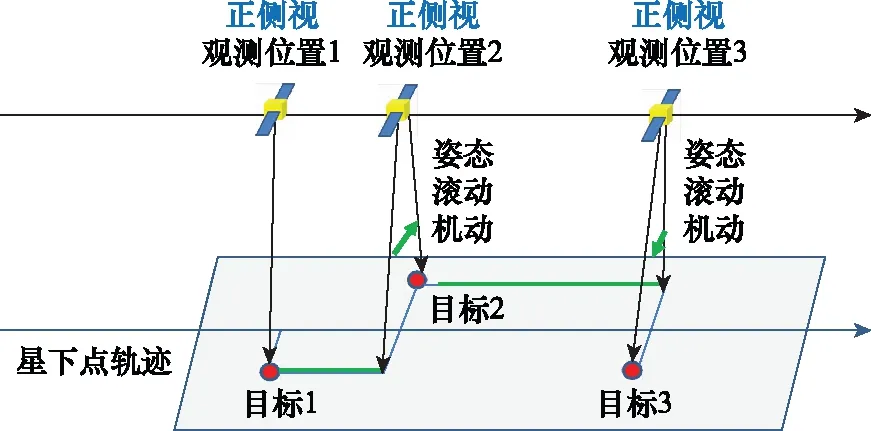
图2 一维自由度的目标观测模式

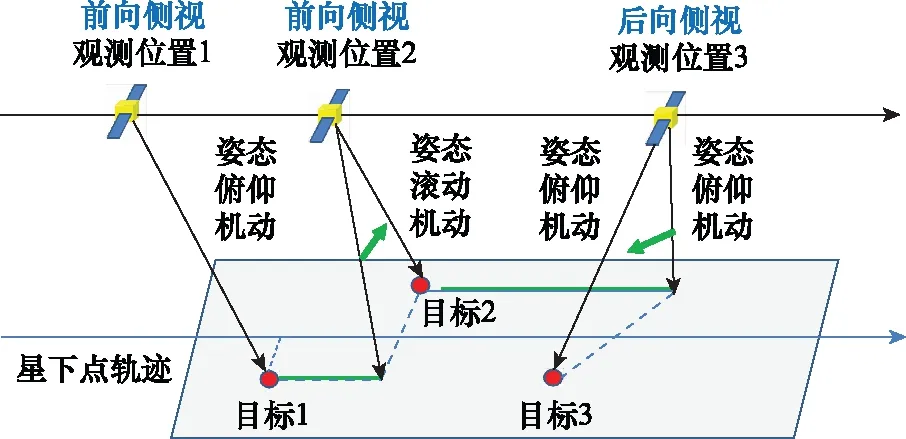
图3 两维自由度的目标观测模式

具备两个轴向姿态机动自由度的敏捷卫星,不但可以观测更大的区域,也可延长对同一目标的观测窗口,因此自主任务规划可以有效提升两维自由度敏捷卫星在轨工作的灵活性,满足更为复杂的任务要求。

本文主要考虑两个轴向的机动能力来实现前向观测与后向观测的在观测过程中的结合,从而提出本文的主要求解方法:前后向链条优化组合方法。该方法在前向观测时采用连续几个处于前向观测的目标组合成为前向的观测序列,同理将同次后向观测的目标组合成为后向观测序列,最后再综合考虑前后向链条的组合,从而形成过境期间的完整观测序列。

1.3 规划模型

通过对于卫星在一次过境中对于多目标的观测收益进行总和计算,对前后向链条优化组合的规划收益进行评价。目标收益函数:

(1)

式中,PI为本次卫星过境的全部目标观测的总收益;Cn为第n个观测目标观测收益;wn为第n个观测目标的权重,其与观测收益的乘积作为第n个观测目标的实际观测收益;tθ,n为向第n个观测目标机动花费的滚动向机动时间;tφ,n为向第n个观测目标机动花费的俯仰向机动时间;k为姿态机动时间消耗权重。该目标收益函数主要的优化方向是尽量优先对于高优先级的目标进行观测,同时将对向该目标进行姿态机动作为主要的约束条件。

1.4 约束条件

在本文中主要考虑的约束包含敏捷遥感卫星的姿态机动范围,也就是滚动轴和俯仰轴向上的最大机动角,该约束实际约束了敏捷遥感卫星可以组成观测链条的前后向范围。

滚动方向约束:

∀θn,|θn|≤θmax

(2)

俯仰方向约束:

∀φn,|φn|≤φmax

(3)

姿态机动速度约束实际约束的是角度机动所花费的时间。

滚动方向机动时间约束:

(4)

式中,Ωθ,n为滚动向的姿态机动速度;Ωθ,n-max为卫星可以达到的最大滚动向姿态机动速度。

俯仰方向机动时间约束:

(5)

式中,Ωφ,n为俯仰向的姿态机动速度;Ωφ,n-max为卫星可以达到的最大俯仰向姿态机动速度。

为了将问题简化,将重点用于任务规划,故这里Ωθ,n,Ωφ,n为平均的滚动向与俯仰向姿态机动速度,不考虑实际在轨过程中的加减速过程。采用较大的姿态机动速度可以获得较短的姿态机动时间,最短为tθ,n-min与tφ,n-min。最大的姿态机动速度会消耗较大的卫星姿态机动资源,获得较低的姿态机动时间消耗权重k。在该问题中,主要考虑以卫星本体进行姿态机动的情况,最大的姿态机动速度不超过4° /s;以及以转台为指向的情况,角度机动范围为5°/s～8°/s。

2 前后向链条多目标观测序列规划算法

2.1 算法设计

前后向链条优化组合方法的目标是充分发挥卫星的姿态机动能力,获得最大化的目标收益。基于以上目标,设计了启发式算法运行的基本规则。

原则 1优先选取高权重目标原则。wn为第n个观测目标的权重,最高为1,最低为0,划分为10个等级。相关权重矩阵默认为星上任务规划前的前置输入。该规则下优先安排观测任务定义价值高的目标。

原则 2链条合成的启发式原则。链条的组合以链条观测点收益最大与卫星姿态机动角最小为规则,选择合成方案。观测点收益由目标权重决定,链条的观测开销由观测链条的长度和方向决定。tθ,n为向第n个观测目标机动花费的滚动向机动时间;tφ,n为向第n个观测目标机动花费的俯仰向机动时间。两者定义了两相邻观测点间姿态机动的所需时间。姿态机动的权重k由向第n个观测目标机动与当前姿态机动方向的比较决定，表达式为

(6)

在本文的仿真场景中,Δθmax=90°,Δφmax=120°。k最大为1,代表卫星在两个方向上都要改变为完全相反的方向,姿态开销最大。k最小为0,代表不用改变姿态就能观测下一点,姿态开销最小。前向链条与卫星运动方向相反,则k值较大,结合姿态机动时间形成总的链接开销。完成组链后链条方向确定,则下一次迭代依据此方向延伸组合链条。

原则3链条边缘点丢弃原则。区域链条组合完成后,分别计算两端各丢弃1点与丢弃2点,返回组链后收益最高的组合,形成最终观测序列。

2.2 算法步骤

算法的流程如图4所示,具体步骤如下。

步骤 1初始化设置,获取多目标的经纬度信息、观测权重及观测开始点信息、卫星的姿态机动能力、每个点目标观测收益,作为任务规划的输入条件。

步骤 2进行初始链条组链,选择本一级观测权重的目标通过最小自动开销计算形成包含2个观测点的元链条。

步骤 3元链条的两端搜索最近的链条或者孤点,以整链收益最高的原则组成新链条,若同一链条为多组链条所选,则选择收益最高组链,如果组成链条节点相同,以收益高的方向组链条。

步骤 4组链后判断链条是否达到局部最优,及是否达到该方向组链长度的上限。满足任意一项则形成局部单条链条,准备开始全局链条组合。如局部收益不是最优，判断是否达到上限,如未达上限,则链条继续增长。

步骤 5进行长链条组合,如最近链接端,姿态开销较大,收益较低链条以丢弃最末节点来组链条,计算丢弃1点与丢弃2点,选组合后最大收益完成组链。返回收益最大链条,如果未超过最大姿态约束则输出链条,如超过,则丢弃两端代价较大点。

步骤 6输出观测序列。

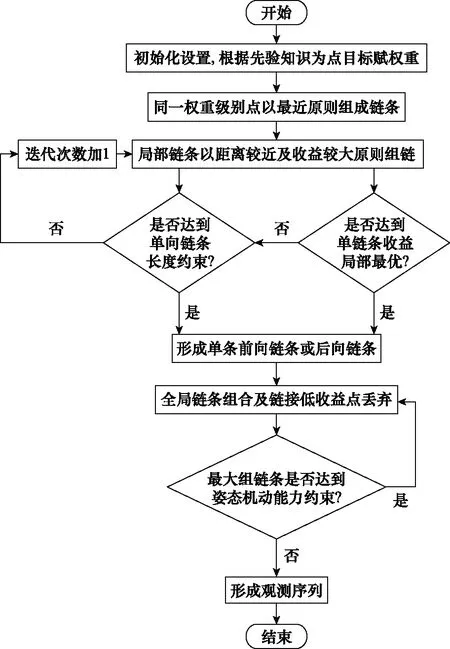
图4 前后向链条优化组合方法规划流程

2.3 算法时间复杂度分析

假设有n候选观测目标,每个目标最坏情况下需要尝试m种链条组合方式才能建立链接。对于每个点根据组合链条的规则进行链条组合符合性的计算,计算m次,时间复杂度为O(log2m)。而针对n个候选目标的时间复杂度,需要完整地循环n次,则总的时间复杂度为O(n·log2m)。由此可见,候选观测目标数量n是影响算法时间复杂度的主要因素,链条组合的尝试次数也对整体的复杂度有影响。

3 仿真校验

3.1 不同机动能力下观测路径分析

仿真卫星轨道高度为800 km,滚动向机动范围θmax=±45°;俯仰向机动范围φmax=±60°。

以不同的机动能力设置了不同数量的待观测目标场景。在场景1中,设置沿星下点航迹两侧500 km内,卫星飞越1 000 km内随机分布30个目标。以低速姿态机动1°/s,2°/s,3°/s,4°/s为输入,进行观测序列路径的规划,结果如图5所示。

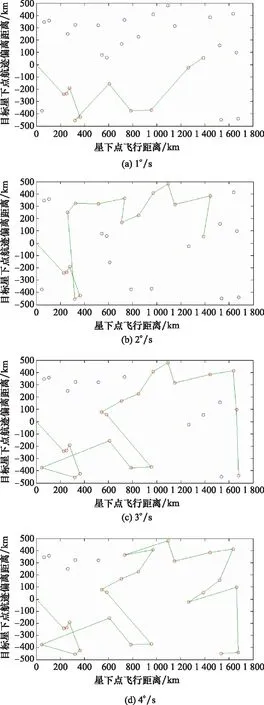
图5 低机动能力下观测序列规划结果

以上结果中,红色的圈点为被选入观测序列的目标点,蓝色圈点为未被选入的观测点。绿色线条为最终组成的完整链条即观测序列。纵坐标的中心0为星下点的轨迹。

针对同一观测场景的观测结果中,在卫星的姿态机动能力较低的情况下,如图5(a)中卫星具备1°/s的姿态机动能力,在30个待观测点的情况下,仅完成对10个左右目标的观测。且观测目标基本分布在卫星侧摆的同一侧。从链条方向上看,主要为前向链条,唯一的后向链条只包含2个观测点。结果表明,卫星在姿态能力较低的情况下,姿态机动能力更适应与飞行方向一致的前向链条。

随着姿态机动能力的增强,在图5(b)和图5(c)中,链条分布于卫星飞行轨迹的两侧。后向链条较少较短。在图5(d)中开始出现包含3个以上观测目标点的后向链条。表明在卫星姿态机动能力到达4 °/s后可以开展更为灵活的成像观测任务。同时可以看到在图5(d)观测路径几乎覆盖了全部的待观测目标点,只遗留5个目标点未被观测。

考虑基于转台,具备更高姿态机动能力情况下可以应对目标量更高的场景。因此,设置包含100个目标的场景2进行仿真。在场景2中,设置沿星下点航迹两侧800 km内随机分布的100个目标。以高速姿态机动为假设场景,分别对姿态机动能力5 °/s,6 °/s,7 °/s,8 °/s输入对目标进行观测序列路径的规划,结果如图6所示。图6(a)和图6(b),在规划覆盖的目标数量上区别较小。姿态机动能力提高之后,链条在卫星轨迹两侧的分布更为平均。图6(c)和图6(d)中都可见有较多后向长链条。其结果与图5(d)呈现的趋势是一致的。后向链条的增加有助于提高整体观测序列的观测收益。

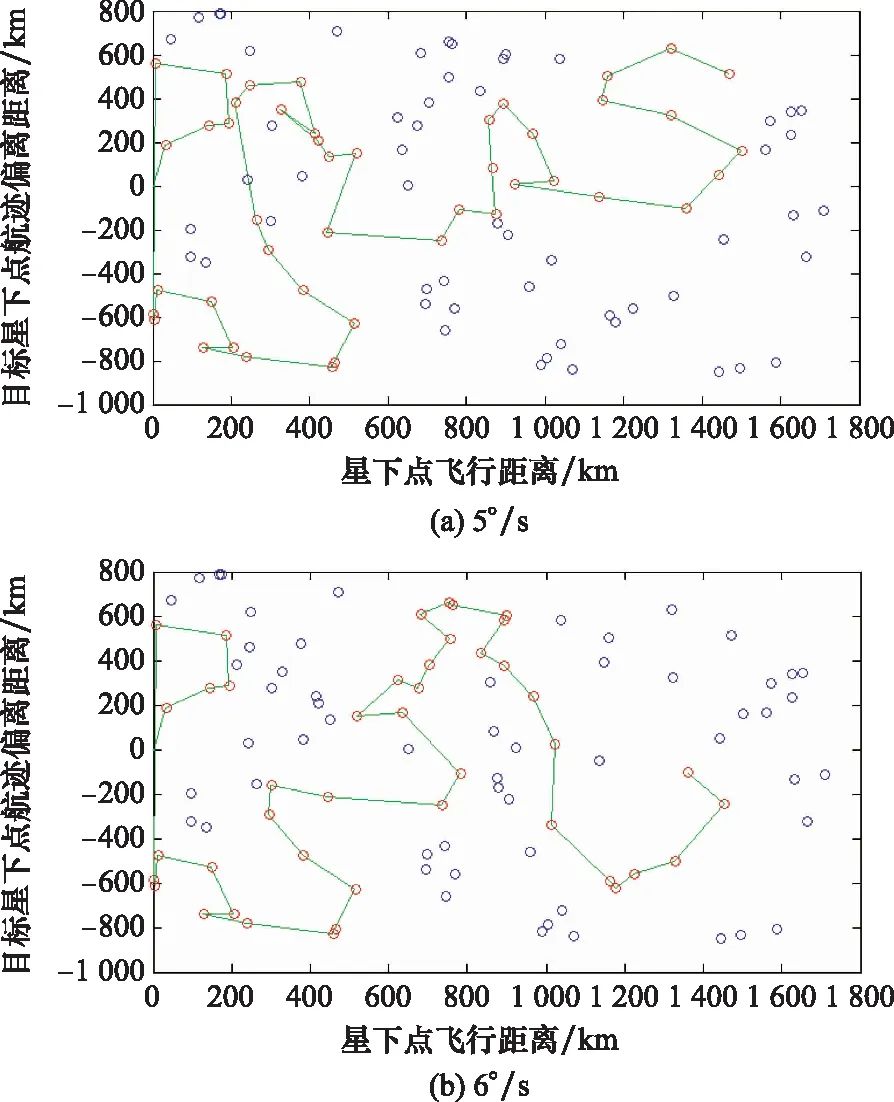
图6 高机动能力下观测序列规划结果

为提高算法的时效性,在仿真中对链条的长度进行了约束,如场景1与场景2中都设置了不大于7跳的链条长度约束。计算开销方面30个目标规划仿真平均规划计算时间约为50 ms,100个目标规划仿真平均规划计算时间约为200 ms。

采用7跳的链条长度约束造成一些较佳链条未被选择,如一些分布较为集中的目标。因此,采用打靶的方法对不同的链条选择原则进行了优化。

3.2 打靶分析

场景1与场景2的仿真中采用单一的链条长度约束设置,仿真结果中出现了一些比较集中分布的观测点未被纳入观测序列的情况,基于场景2进行了不同链条长度约束下的打靶分析。每种约束下,对于不同的观测驻留时间,各进行1 000次随机分布目标的观测收益计算。链条组合打靶分析结果如图7所示。经过打靶分析,在驻留时间较短的场景下,前向和后向链条长度接近的组合方式可获得高的观测收益。随着观测时间的增加,后向链条的长度增加有助于提高观测效能,效果在增加3～5跳时最为明显，如图7中最顶部分所示。在前向链条与后向链条的长度约束都设置到15次时,观测收益已呈现出下降趋势。依据仿真结果,前向链条的长度在6～9跳之间,后向链条的长度在7～13跳之间组合可以获得较好的组合收益。链条较短时容易遗漏密集分布的观测目标点。在链条较长时,由于最后组链时只使用丢弃1点和丢弃2点原则,造成已形成的链条难以进一步丢弃影响收益的观测点。最后,计算开销方面100个目标规划仿真平均规划计算时间约为200 ms,最大不超过300 ms。

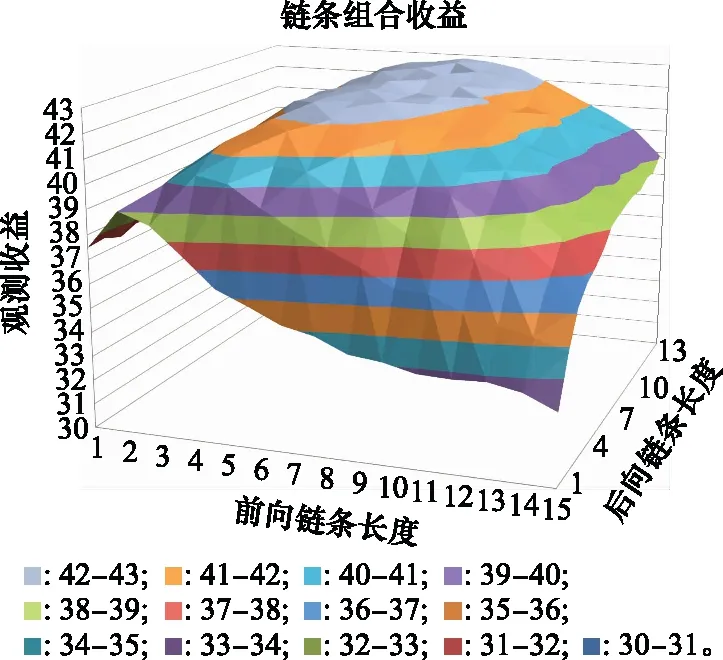
图7 链条组合分析

3.3 观测时间对链条的影响

对于不同凝视时间下的链条长度的置信度进行分析,分析结果如图8所示。

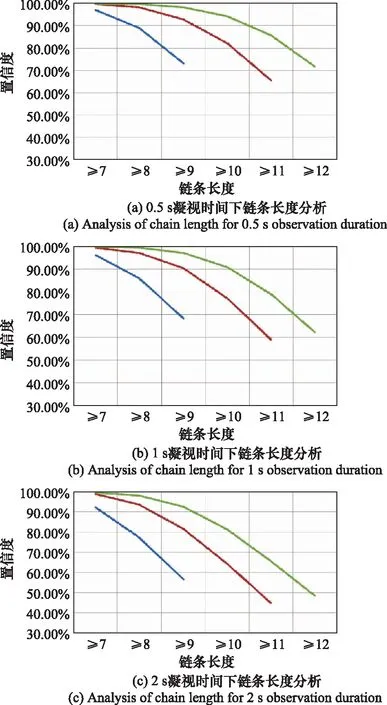
图8 观测时长分析

图8(a)中在凝视时间为0.5 s时,结果分布在优于85%的置信区间内,30个目标,选用的链条长度应小于7跳;40个目标,选用的链条长度应小于10跳;50个目标,选用的链条长度应小于11跳。

图8(b)～图8(d)中,随着对于同一个目标点的观测驻留时间的增加,不同目标数量下的链条选用长度都进一步缩减。观测模式中增加目标凝视模式,适用的链条长度缩短。

4 结 论

本文从工程应用出发,针对具备两个轴向自由度的敏捷遥感卫星在一次过境对多目标的观测,提出了一种以其姿态机动能力为约束的前后向链条优化组合方法。

本文建立了问题模型与目标函数,并完成了前后向链条优化组合方法的算法设计。经过仿真表明算法有效,可以依据在轨条件实现实时的观测路径规划。同时在固定链条长度约束下,任务规划方法会导致一些较佳链条未被选择的情况。因此，对链条长度进行优化,得出了特定场景下的前后向链条长度的选择区间。最后，考虑了在不同凝视情况下对链条长度的选择影响情况。综上,前后向链条优化组合方法有效,计算开销在星上条件下都小于1 s,可应用于敏捷卫星面向大量点目标的在轨自主任务规划应用。未来工作中,需要在链条针对目标分布的自适应选择方面开展进一步的研究。