基于载荷谱的转向架焊接构架疲劳可靠性分析*
2021-05-06辛俊胜商跃进杨朋朋张洁娟
辛俊胜,商跃进,薛 海,杨朋朋,张洁娟
(兰州交通大学机电工程学院,兰州 730070)
0 引言
转向架是铁路机车车辆的重要组成部分,而焊接构架又是轨道车辆转向架的主要零部件之一,起着承载、连接以及传递载荷的作用[1]。轨道车辆的车轮在运行一段时间后会因滚动接触、牵引、制动和车辆振动等多种因素的影响而产生磨耗,使得轮轨间作用力增大,从而导致焊接构架在服役过程中应力随之增大,容易产生疲劳裂纹,影响车辆的运行安全。
在转向架疲劳寿命研究当中,相关学者做了诸多研究:卢耀辉等[2]参照UIC 515-4标准对比分析了考虑焊缝和不考虑焊缝的客车构架疲劳强度,并绘制构架Goodman曲线;刘旭等[3]选取构架箱体梁为研究对象,以静强度为基础建立了主焊缝关于名义应力、结构应力和缺口应力的三种应力模型,并进行寿命预测;文献[4-5]根据焊接结构疲劳失效的特点发展了热点应力和缺口应力的分析方法,排除了接头名义应力的分散性。焊接件的焊缝是最容易出现疲劳破坏的部位,而且疲劳破坏通常发生在焊缝的焊趾处,并沿着焊趾在厚度方向上扩展[6];文孝霞等[7]对焊接构架焊缝参数进行敏感性分析,表明焊接厚度和焊接熔深将直接影响焊缝的寿命;王红等[8]选用热点应力法对焊接构架疲劳寿命进行了预测,由于热点应力法考虑了应力峰值的影响,因此相对于名义应力法精度有所提高。
考虑随机变量的不确定性对焊接构架寿命的影响,文章以应力强度理论为基础,建立可靠性状态函数,并采用一次二阶矩法对焊接构架薄弱焊缝处进行可靠性分析,以概率的形式描述构架运行安全性,并对随机变量进行灵敏度分析。该方法可为转向架焊接构架的设计、结构改进及制定维护策略提供参考。
1 可靠性设计理论
1.1 可靠性分析
可靠性分析是通过由状态函数的概率分布求出的可靠性概率,其结果是由影响状态函数的随机变量所决定的[9]。状态函数由式(1)表示:
Z=R-S=g(X),X=[x1,x2,···,xn]
(1)
式中,R为结构强度;S为工作应力;X为随机变量参数,n为影响可靠度参数的数量。
一次二阶矩法是求解可靠度常用的解析方法,通过将非线性的状态函数展开成线性状态函数,从而计算出可靠性指标并求出可靠度。

(2)
则状态函数的均值和标准差为:
μZ=g(μX)
(3)
(4)
状态函数g(X)对各随机变量X求偏导为:
(5)
则可靠性指标和可靠度分别为:
(6)
(7)
1.2 可靠性灵敏度分析
可靠性灵敏度反应了各随机变量参数对机械可靠度影响的大小,灵敏度绝对值越大,说明该参数对可靠性影响越明显。根据可靠度计算公式推导出各随机变量均值和方差的灵敏度计算公式分别为式(8)、式(9):
(8)
(9)
其中,
(10)
(11)
(12)
2 构架静强度分析
2.1 有限元模型建立
高速动车组转向架焊接构架主要由管状横梁、纵向连接梁和侧梁焊接为H型,为了提高计算效率,依据焊接构架结构特点及受载情况,对不影响求解结果的一些孔以及圆角结构等进行简化处理。根据构架整体尺寸,并考虑焊缝处应力仿真结果的准确性,在Hypermesh软件中,采用C3D8R单元进行有限元网格划分,共生成 918 501个单元,432 098个节点。图1为转向架有限元模型。

图1 焊接构架有限元模型
2.2 载荷工况及边界条件
参考UIC 615-4与EN 13749标准,考虑了电机载荷、焊接吊座载荷等外载荷,组合共得到直线驱动、直线制动、曲线驱动、曲线制动等49种运营工况[10],在这里只列出载荷条件复杂的第49载荷工况下所对应的应力云图,如图2所示。

图2 第49种工况下应力云图
构架局部应力分析如表1所示[11],由表1可知转臂定位座立板与侧梁下盖板焊缝连接处的应力幅值最大,因此选取此处来代替整个构架进行可靠性分析。

表1 构架局部应力分析
3 载荷谱
3.1 车辆动力学模型建立
根据350 km/h公里级车辆表2的相关参数建立的高速动车组多体动力学模型如图3所示。
随着互联网电子商务的不断发展,自助售卖机和各种自助服务已基本成熟,提供了适宜电商与自助家庭化的物质保障,在大中型城市已经广泛应用。

图3 车辆多体动力学模型
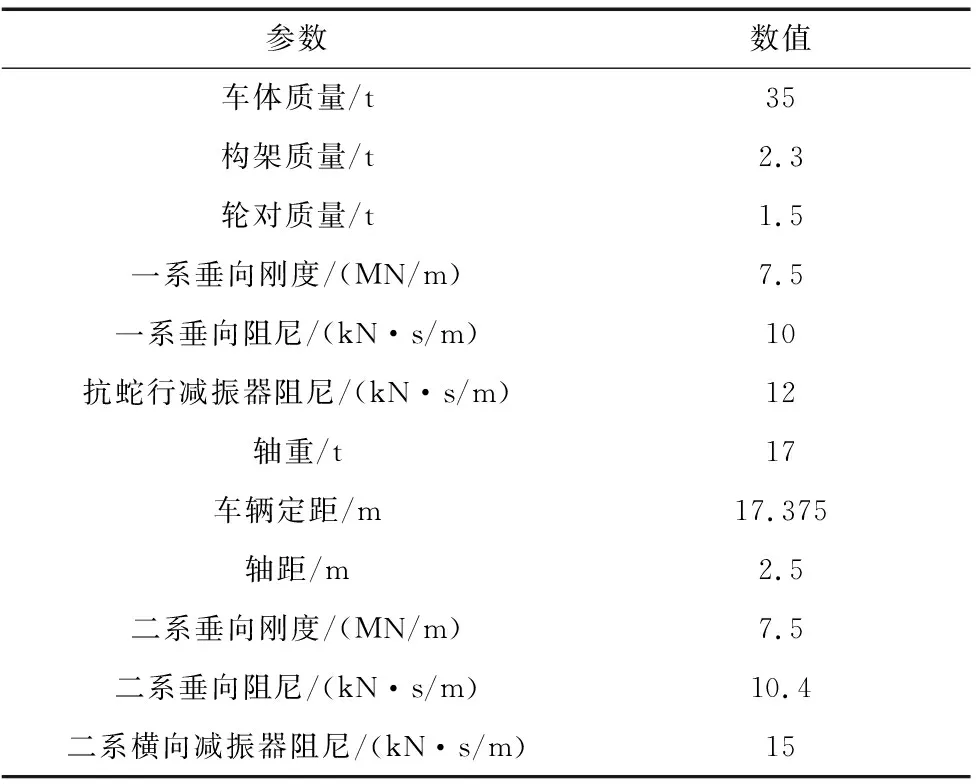
表2 车辆主要参数
3.2 分级载荷谱
选取直线运行以及曲线通过两种工况类型,直线工况下设置列车行驶速度为350 km/h,曲线通过工况下设置列车行驶速度为300 km/h;列车行驶时间均设置为50 s。高速动车组动力学模型转臂处的采样频率为200 Hz,载荷数据采集时间为50 s,因此共得到1.0E4个载荷信号并,对转臂定位座焊缝区域进行分级统计。
由于采集到的载荷数据样本量较大,采用8级谱分级数所反应的载荷数据不完整,因此,选择载荷谱分级数为16级,以5%的载荷幅值作为门槛值[12],对转臂定位座焊缝区域在直线运行条件以及曲线运行条件时的载荷频次分别进行分级统计,得到两种运行条件下的16级载荷谱如表3所示。

表3 转臂定位座位置载荷谱

续表
3.3 载荷与应力转化关系
对构架进行可靠性分析需要得到相应的应力谱,因此要将载荷谱转化为应力谱。转向架构架动应力与动载荷之间具有线性对应关系,因此可根据有限元的计算结果与所加的载荷值求解出与之对应的比例系数,具体结果按照式(13)进行求解:
(13)
式中:σeqc代表相应的Von-mises应力;F代表标准规定的相关载荷。为了得到更加精确的焊缝区域的应力值,本文采用子模型法对转臂定位座进行分析。根据圣维南定理,必须满足切割边界远离模型要研究的应力集中的区域[13],对转臂定位座与箱型梁下盖板处建立详细的角接焊缝结构并进行精细网格划分。图4所示为所建子模型有限元模型(包含4条角接焊缝)。判断子模型建立正确性的方法是对比切割边界区域的应力应变结果与全局模型是否一致,如果结果一致,则认为该子模型是有效的。通过验证得出该有限元模型的边界满足子模型要求,如图5所示。
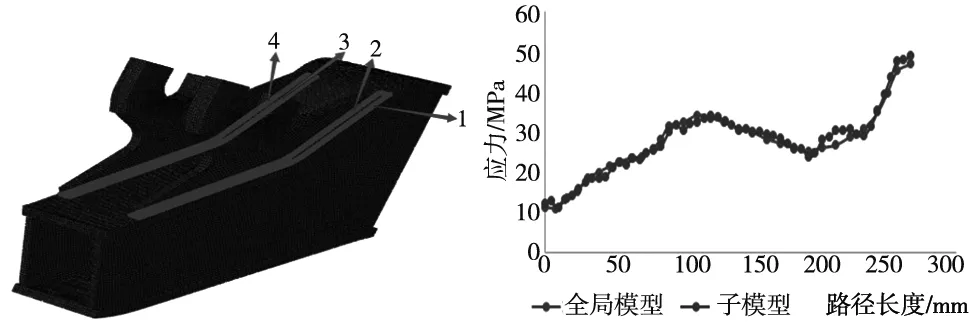
图4 子模型有限元模型 图5 子模型边界验证
所提取子模型转臂定位座与箱型梁下盖板连接焊缝的应力值,由于最大应力节点出现在第二条焊缝所在位置,因此在这里只列出第二条焊缝所有节点随焊缝长度变化的应力值如图6所示,选取最大应力值所对应的节点进行载荷转换系数K的计算。根据公式(1)计算得到载荷-应力转换系数为K=1.71。

图6 第二条焊缝节点应力值
4 可靠性灵敏度分析
转臂定位座焊缝处等效应力计算公式为:
(14)
式中,L为车辆运营公里数;L1为实测公里数;N为循环次数,取200万次;m为材料常数,取m=3.5;K为转换系数;Fi为第i级载荷谱幅值;ni为第i级载荷幅值对应的循环次数[11]。
则可靠性状态函数为:
(15)

表4 参数表
通过一次二阶矩法计算焊接构架可靠度随运行里程的变化曲线如图7所示,并通过Monte-Carlo法进行验证。由图7可以看出:
(1)车辆运行至1000万公里以后,焊接构架可靠性开始降低,当运行至1200万公里时可靠度为0.998 7,满足3σ设计要求;
(2)两种方法计算得到的可靠度结果非常接近,故采用一次二阶矩计算可靠度结果可以接受。

图7 可靠度变化曲线
图8、图9分别为各随机参数均值和方差随运行里程对可性度的灵敏度曲线,由图8和图9可以看出:
(1)各参数均值对可靠度的影响中,转换系数k对可靠性影响最为明显,许用应力r影响最小;
(2)各参数方差对可靠度的灵敏度均为负值,且载荷-应力转换系数k灵敏度绝对值最大。

图8 参数均值灵敏度

图9 参数方差灵敏度
5 结论
(1)对转向架焊接构架进行有限元分析,得到转臂定位座焊缝处应力幅值最大,进而对应力薄弱区采用子模型法进行分析计算,得到了更加精确的焊缝区应力值,并求得载荷-应力转换系数K=1.71。
(2)以强度-应力干涉理论为基础,建立可靠性状态函数,并采用一次二阶矩法对转臂定位座焊缝处进行可靠度计算和灵敏度分析,并采用Monte-Carlo法验证了一次二阶矩计算可靠度的准确性。
(3)车辆运行至1200万公里时,焊接构架可靠度为0.998 7,满足3σ设计要求,转换系数均值和方差对可靠度的影响最为明显。
