亚声速条件下十字形伞充满时间系数的解算方法及仿真验证

喻东明，马啸民，杨 品

（1.航空工业航宇救生装备有限公司空降空投技术研发部,襄阳441003；2.航空工业航宇救生装备有限公司应用技术部,襄阳441003）

在降落伞的工作过程中，充气阶段是最为复杂的一个阶段，在该过程伞衣的结构变形和伞衣周围的流场变化相互耦合，使得难以精确建立伞衣充气的理论模型[1-3]。目前,对于降落伞充气性能的研究主要是通过一些实验结果的统计分析来获取的,充气性能与开伞条件之间的关系也是通过试验结果统计、拟合出来的。这使得充气时间、伞衣投影面积变化的一些经验公式存在着一定的局限性[4]，只能在某型情况下适用。

十字形伞最早由法国人提出，具有工艺简单、稳定性好、开伞动载小等优点，被广泛应用于飞机阻力伞、航弹伞及投物伞领域。该伞的结构简单，伞衣由两个相同的矩形织物面组成，这两个矩形织物面彼此成直角相交连接，形成一个有4 个相同矩形幅的平面，结构示意图见图1。

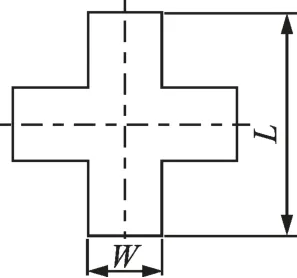
图1 十字形伞示意图Fig.1 Schematic diagram of cruciform parachute

十字形伞的充满时间与开伞动载、充满距离关系密切，特别是对于水平着陆的飞行器减速而言，充满时间的长短则直接影响着滑跑距离消耗的多寡。因此，通过放伞速度以及伞衣面积评估十字形伞充满时间对于研究飞行器着陆滑跑性能以及十字形伞开伞载荷特性具有极其重要的意义，在目前缺乏十字形伞充满时间参数的条件下评估其充满时间则需要进行充满时间系数的解算以及验证。

1 解算方法及结果

1.1 经验公式的简化

降落伞充气过程是一个流进伞衣的空气体积大于流出的空气体积而使伞衣体积逐渐扩大的过程（图2），伞衣内空气的平衡方程如下

式中：V 为伞衣体积；rd为伞顶孔半径；v∞、vq为自由气流速度和透过伞衣织物的平均气流速度；n1、n2为入口气流和通过伞顶孔气流速度修正系数。

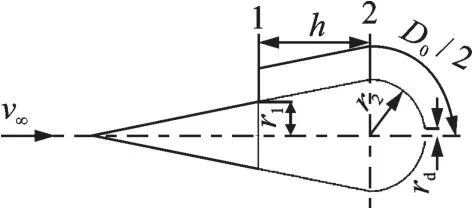
图2 伞衣充气模型Fig.2 Canopy inflation model

从以上平衡方程可以看出，伞衣体积V 越大则充满时间越长，来流速度v∞越大则充满时间越短。降落伞的充满时间指伞衣拉直后从底边充气开始至伞衣完全张满结束所经历的过程时长。降落伞的充满时间与拉直速度成反比，与其几何结构尺寸成正比。降落伞充满时间的经验公式如下

式中：v1为拉直速度；D0为伞衣名义面积；K 为伞衣充满时间系数；为简便起见，n 取1。

根据充气过程中物-伞系统的减速程度，降落伞充气分为“有限质量”充气和“无限质量”充气。“无限质量”充气引起的物-伞系统减速可忽略不计，而“有限质量”充气引起的物-伞系统减速则非常明显。

由于“无限质量”充气引起的物-伞系统减速可忽略不计，对于“无限质量”充气、亚声速工况下的十字形伞，其充满时间的经验公式则可简化为（以开伞速度vf代替拉直速度v1）

1.2 解算过程及结果

目前缺乏十字形伞充满时间系数K 的取值规范，难以事先评估不同伞衣面积十字形伞的充满时间，制约着飞行器着陆滑跑性能以及十字形伞开伞载荷特性的研究。因此，需要结合充满时间的实测值通过式（5）解算出充满时间系数

根据定义，伞衣面积与伞衣名义直径的关系如下

将充满时间实测均值μ、开伞速度vf以及由式（5）计算出的名义直径D0代入式（4），容易得出充满时间系数K=9.47。

1.3 圆整处理

以上得出的充满时间系数K 含有小数位，需要圆整后才便于其在工程上的推广应用。

在充满时间的实际判读过程中，起始影像中难免会伴有部分伞衣、伞绳拉直的画面，即充满时间的判读起点有时会前移，导致其实测值比真实结果偏大。鉴于此，充满时间系数K 应向下圆整为9。

2 校验对比

2005 年某型阻力伞（简称15 型）进行了飞机着陆放伞试验，该型伞伞衣为十字形，面积20 m2，放伞速度（即下文中所称开伞速度）一般为300 km/h（83.3 m/s），处于亚声速阶段。

试验过程中利用高速摄像机拍摄了阻力伞放伞过程的影像，通过判读伞衣从底边充气（图3）开始至完全张满（图4）所经历的影像帧数（每秒125 帧）换算得出的充满时间的实测值如表1所示。

图3 伞衣底边充气Fig.3 Inflation at the bottom of the canopy

图4 伞衣完全张满Fig.4 Inflated canopy

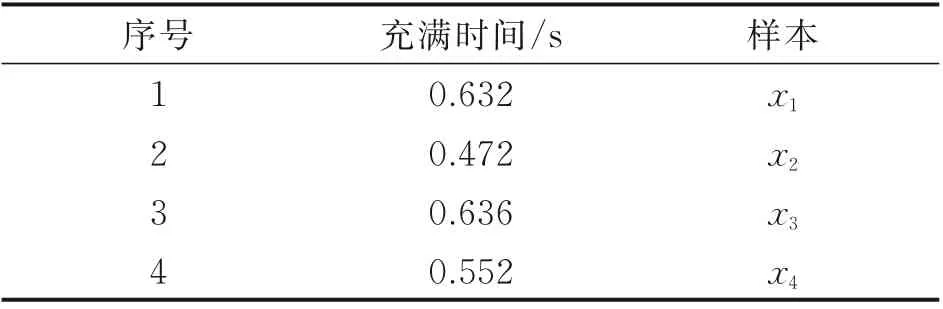
表1 阻力伞充气时间实测值Table 1 Measured value of inflation time of drag para-chute

将充满时间看作连续性随机变量X，假设其服从正态分布，根据式（6，7）可以计算出以上4 个样本的均值μ 为0.573，样本标准差σ 为0.077，95%置信区间（0.419，0.727），数据离散程度不大。可以认为，该组小样本量数据作为后续解算的依据是可信的。

根据相关文献资料介绍，美国标准T-10 型伞兵伞为平面底边延伸伞，与十字形伞在伞型分类上同属于密实织物伞，其充满时间系数K 通常取8。通过伞型比对可知：十字形伞充满时间系数的解算结果稍大于已有的密实织物伞经验值，这是因为十字形伞和平面底边延伸伞虽同属密实织物伞，但前者在伞衣张满后叶片间会形成缺口，加大了流出空气的体积，从而延缓了伞衣体积扩大的进程，导致充满时间延长，充满时间系数K 稍大。

15 型伞与T-10 型伞兵伞在相同开伞速度条件下的充满时间明显存在差异，这主要是因为两者的名义直径相差太大导致的（见表2），与十字形伞充满时间系数的解算结果稍大于已有的密实织物伞取值结果的结论不矛盾。

表2 T-10 型伞兵伞与15 型伞Table 2 T-10 paratrooper and 15 paratrooper

为了便于估计不同伞衣面积的十字形伞充满时间，将式（5）变换为

将开伞速度及K 值代入，式（8）可进一步简化为

一定开伞速度（tm）条件下不同伞衣面积（S）的十字形伞充满时间曲线如图5 所示。

注：以上结果是在“无限质量”充气条件下获得的，对于“有限质量”充气条件下十字形伞充满时间的解算，需在开展进一步研究的基础上对以上结果予以适当修正。

3 仿真验证

前文通过利用小样本量实测值解算十字形伞充满时间系数的方法得到了相应结果，该结果是否准确、可信，除完成初步校验外，还应进行一定范围的仿真验证。

以另一型别十字形阻力伞放伞为研究对象，建立仿真模型，模拟阻力伞从开始充气至张满过程，得到伞衣张满时间，对得到的伞衣张满经验公式进行仿真验证。

3.1 数值仿真理论基础

本文采用LS-DYNA 软件SALE 算法进行流固耦合仿真。该算法由流场控制方程、网格控制方程、结构控制方程组成。流场控制方程由质量方程、动量方程和能量方程组成，分别为[5-9]

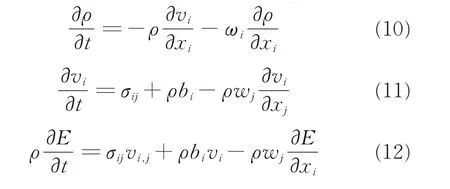
式中：vi为物质速度，wi为相对速度，wi=vi-ui，ui为 网 格 速 度；σij为 应 力 张 量，σij=-ρδij+μ(vi,j+vj,i)；bi表示单位体积力；δij为Kronecker δ-函数。

网格控制方程为

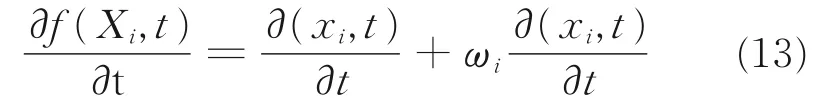
式中：Xi为拉格朗日网格坐标；xi为欧拉坐标；wi为相对速度。材料运动速度由膜的结构动力学特性决定。结构控制方程为

式中：M、C、K 分别表示单元质量、阻尼模量和弹性模量，F 为膜单元所受合力。

3.2 仿真模型建立

阻力伞放伞仿真模型由飞机、阻力伞系统、地面、流场域4 部分组成，对飞机放伞区域的流场网格进行加密，如图6 所示[10]。

3.3 求解关键字设置

在提交LS-DYNA 求解器计算前，需进行关键字设置，包括各组成部件的单元算法、材料模型及不同部件间的耦合、接触、连接、动网格、边界、加载、沙漏、输出等求解关键设置，以下对其中几类关键设置进行说明。

(1) 流固耦合：选择考虑透气性的适合织物类仿真的11 号流固耦合算法。根据试验测得的该伞衣压差与透气量数据，参考Ergun 公式得到伞衣透气性的黏性和惯性两个参数。

(2) 流场域填充：SALE 方法进行流场建模的方式和ALE 方法直接进行网格划分不同，SALE流场域只需设置3 个维度方向的位置和网格数量，再将所定义的物质材料（空气）对该部件进行填充。

(3) 流场域运动：在定义流场域部件，会设置其所在的坐标系，若该坐标系运动，则流场域随之运动,若该坐标系静止，则流场域静止,以此途径实现空气域随飞机放伞系统同步运动。

(4) 接触：放伞过程中伞衣自身、伞衣和伞舱、伞绳和伞舱、伞衣和地面等会产生接触，本文用到的接触有自接触、面面接触和点面接触。

(5) 动网格：通过LS-DYNA 提供的SALE 相关关键字进行设置，使得流场域网格与飞机同步运动，避免大规模流场域网格。

(6) 加载：设置飞机和伞系统的初始运动速度，本次计算设置其速度为300 km/h。

(7) 输出：伞衣受力传递到伞绳，并通过连接带叉带、连接带主部、连接绳索传递到飞机，设置输出连接绳索首单元的受力曲线，并每隔0.015 s 输出d3plot 文件。

设置完求解关键字，形成K 文件，将其提交LS-DYNA 求解器进行计算。

3.4 计算结果及分析

在后处理中打开d3plot 文件，可动画播放阻力伞充气张满的工作过程。以阻力伞伞顶被引导伞拉出时刻为系统零点，当t=0.68 s 时，伞衣开始充气，当t=1.30 s 时伞衣充气张满，如图7、8所 示[11-13]。

图7 伞衣开始充气Fig.7 Canopy starting to inflate

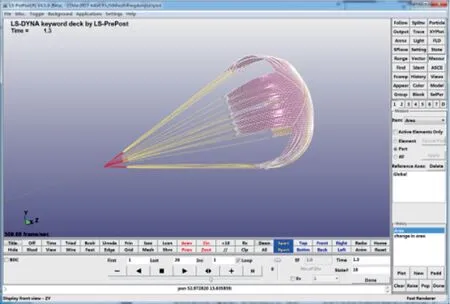
图8 伞衣充气张满Fig.8 A fully inflated canopy

由此可知，伞衣张满时间为0.62 s。该型阻力伞伞衣面积为28 m2，按照式（9）计算其张满时间为0.65 s，仿真与理论计算较为接近，相对误差为4.6%。

4 结 论

目前十字形伞充满时间系数缺乏取值依据、充满时间不易估算，利用亚声速条件下充满时间实测值可解算出十字形伞充满时间系数，其圆整结果稍大于已有的密实织物伞经验值。通过一定程度的仿真验证表明：利用十字形伞充满时间系数圆整结果得出的充满时间基本准确、可信。

本文只讨论了一定开伞速度下十字形伞充满时间的估算问题，对于不同开伞速度、不同伞衣面积十字形伞充满时间的预估，可以在本文结果的基础上利用充满时间与拉直速度vf的反比函数关系间接计算。