降雨条件下飞机尾涡演化数值模拟研究

周金鑫，陈迎春,2，李 栋，张泽宇，潘卫军

（1.西北工业大学航空学院, 西安710072；2.中国商用飞机有限责任公司, 上海200126；3.中国民航飞行学院空中交通管理学院, 广汉618307）

尾涡是飞机产生升力的副产品，是一对反向旋转的涡流。当后机遭遇前机的高强度尾涡时，会对其飞行姿态产生不可忽视的影响，如发生滚转，使其无法改出，这对处在起飞和降落阶段的后机来说是致命的。因此，尾流影响着机场容量与进近阶段的飞行安全[1]。国际民航组织规定了相对保守的尾流间隔，其制定依据主要是基于常见的气象条件对尾涡演化的影响规律，如中等或较弱强度的大气湍流和温度分层等干净大气条件。为了缩减尾流间隔，数值模拟方法被应用到尾涡演化的研究中，Gerz 等[2]在不同的速度分量方向采用不同的能谱来初始化湍流场，通过更换计算域尺寸及网格尺寸的方法来研究尾涡演化过程。Hennemann 等[3]基于大涡模拟结果提出尾涡变形与大气湍流等级和温度分层有关，也受到涡对的下降速度和涡核半径的影响，改变涡核尺寸直接影响尾涡强度的演化。Han 等[4]通过添加人工外部力的方法产生湍流初始场，并在此基础上研究尾涡的演化过程。林孟达等[5]采用自适应网格,基于大涡模拟研究了不同大气湍流强度和温度分层下的尾涡演变规律。可见，大气湍流和温度分层对尾涡演化有重要影响。然而，对于降雨等特殊的气象条件在尾涡演化中起到的作用，国内外的相关研究较少。

目前，考虑降雨条件的尾涡研究，主要通过对尾涡场中雨滴的雷达观测或模拟来反演和监控尾涡的强度和位置。Barbaresco 等[6]利用高分辨雷达观测了降雨率分别为1、5、20 mm/h 进近阶段的飞机尾涡，得到了尾涡的多普勒谱宽。Schneider 等[7]建立了尾涡反演的经验模型，利用雷达扫描得到雨滴多普勒频谱反演了尾涡的环量。但由于分辨率的限制，雷达观测只能的获得尾涡宏观的速度和位置信息，无法捕捉降雨条件下尾涡的演化细节。在国内的研究中，国防科技大学在研究雨雾天气的尾流雷达信号模拟方面做了很多工作，如Li 等[8]对尾涡附近雨滴的速度和加速度进行了估计，提出了一种基于垂直指向雷达环量反演方法来监控尾涡；屈龙海[9]研究中建立了雨滴运动方程并忽略其对尾涡的影响，基于二维尾涡速度场实时更新雨滴的位置信息，通过对尾涡雷达信号模拟来研究其强度。然而，雨滴与尾涡运动是耦合的，两者存在动力学上的相互作用，雨滴对尾涡演化存在一定程度的影响，在计算中不可简单地忽略。因此，为了相对准确地捕捉降雨条件下尾涡的演化规律，雨滴与尾涡的相互作用需要予以考虑，这无论对补充特殊气象条件下尾流间隔数据，还是为尾涡的雷达观测提供理论支持都有实际意义。

本文引入了多相流模型，通过添加空气相与雨相之间拖拽力考虑了尾涡与降雨的相互作用，利用数值模拟方法研究了不同降雨强度条件下，尾涡演化过程中环量、涡量和涡核附近速度分布和下沉速度等特征量演变规律，也分析了尾涡对雨滴的分布浓度及运动轨迹的影响。

1 控制方程

实际中，空气中的雨滴或雾滴是以离散的形式存在，而采用欧拉多相流方法，各相被假设为连续介质且是相互渗透的，因此体积分数将作为待求解未知量出现在控制方程中。欧拉方法中的各流动相的输运需要满足连续性和动量方程，不同相的耦合作用通过施加相间拖拽力实现。

1.1 空气相方程

对于空气相，也就是尾涡流场的求解采用大涡模拟，并使用动态亚格子模型封闭方程组，相间的拖拽力通过在动量方程中添加源相体现。控制方程为

式中：下标r 表示雨相；a、D 和Re 分别表示雨相体积分数、雨滴直径、相对雷诺数。需要说明的是，在实际降雨条件下，雨滴包含丰富的长度尺度，直径主要介于0.01～6 mm 之间，大致呈高斯分布[10]，本文取其平均数0.5 mm。CD为阻力系数，模拟雨滴在空气中运动时受到的阻力效应，其值为

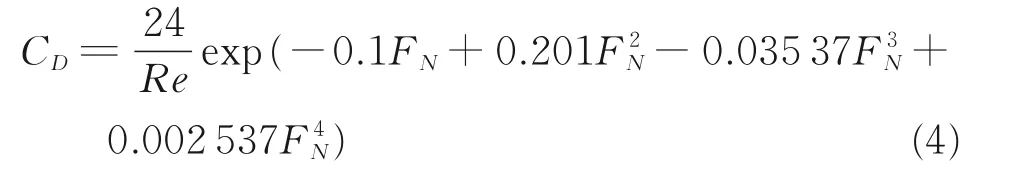
式中FN=log(1+Re)。在动量方程的时间项和对流项中没有出现空气相的体积分数，这是由于雨滴相对空气的体积占比很小，为了简化方程，不考虑其对动量输运的影响。

1.2 雨相方程

对于雨相的模拟，通过ANSYS Fluent UDF添加两个标量输运方程求解

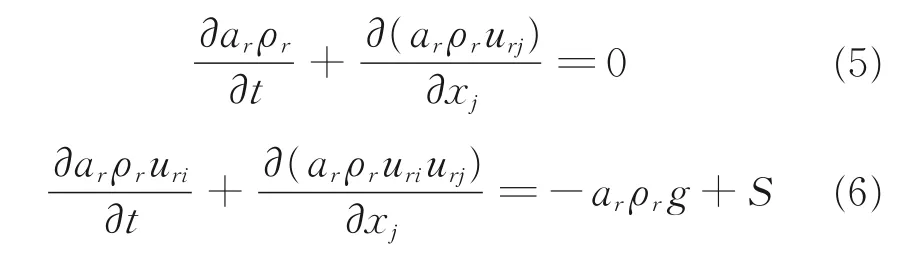
式 中，arρr整 体 可 看 作 为 有 效 密 度，g 为 重 力 加 速度，也就是说源相考虑相间拖拽力和重力的影响。此欧拉多相流模型也被Huang 等[11]的风驱雨研究中所采用，其结果与Blocken 等[12]的现场测量数据吻合良好。

2 初始和边界条件

2.1 尾涡模型

根据椭圆翼假设，前机的初始环量为

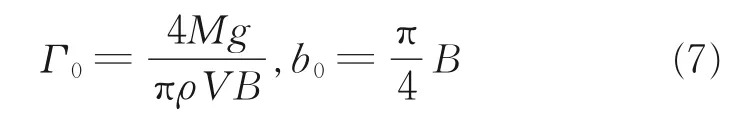
式中：Mg 为飞机重力，V 为飞行速度，B 为翼展。尾涡初始流场采用Burnham-Hallock 涡模型模拟，单涡流场的切向速度由初始环量Γ0、涡核半径rc和到涡心距离r 决定，其表达式为

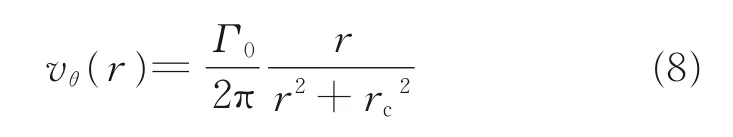
选取中型机的尾涡作为研究对象，设尾涡参数为初始环量Γ0=200 m2/s，涡核间距b0=26.7 m，涡核半径rc0=0.11b0=3 m，尾涡初始下降速度w0=Γ0/(2πb0)=1.19 m/s，特 征 时 间t0=b0/w0=22.4 s。将左右两个以涡核为中心的涡场叠加可得到前机尾涡速度场，如图1 所示。

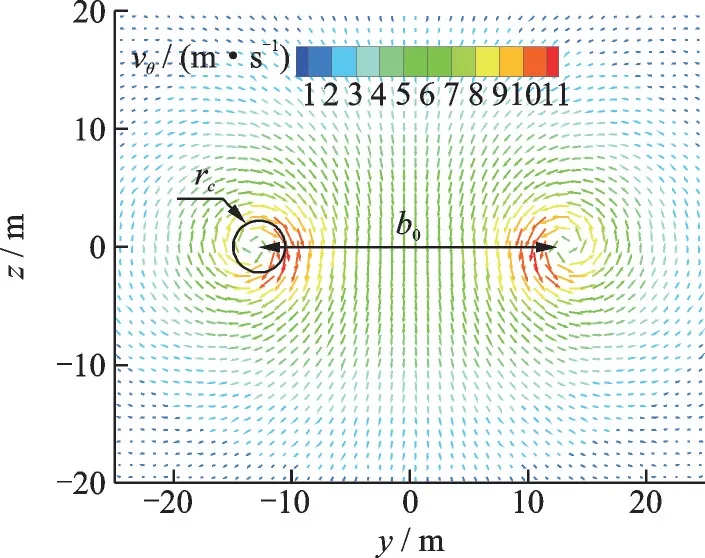
图1 初始切向速度vθ 分布Fig.1 Profile of initial tangential velocity vθ

2.2 大气湍流场

大气湍流强度对尾涡耗散进程有重要影响，因此在降雨条件下也应予以考虑。将尾涡速度场与大气湍流场叠加作为空气相的初始条件。

初始大气湍流场可看作均匀各向同性，采用Rogallo 提出的速度场构造方法[13]。在本文中，设大气湍流满足的目标能谱为文献[14]提出的修正的冯卡门能谱

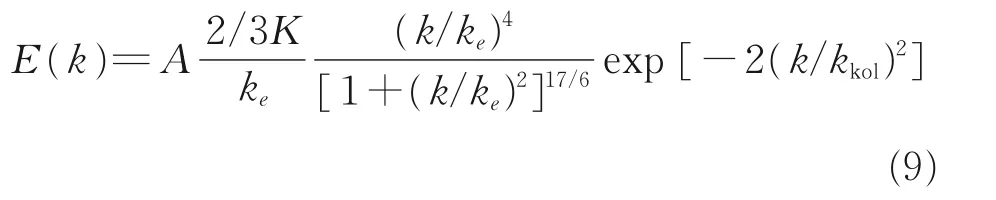
式 中：ke为 波 峰 波 数，取 为(2π/100) m-1；kkol=(ε/ν3)1/4为Kolmogorov 波 数。参 数A 与K 的 乘 积由以下关系式确定。

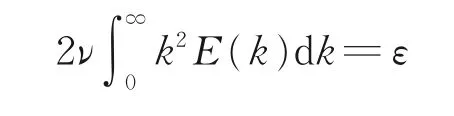
大气湍流场在边长为256 m 的立方体网格上生成，3 个方向的网格数均为256，网格尺寸1 m。网格能分辨的最大波数为（2π/256）m-1，能分辨的最小波数为π m-1，本文目标能谱的惯性子区被包含在区间[2π/256，π] m-1中，说明大气湍流场的计算域的边长与网格尺寸选择合理。首先在谱空间构造初始大气湍流场，谱空间速度分布为

当波数处于能谱惯性子区时，均匀各向同性湍流特性只由唯一参数湍动能耗散率ε 决定，为了能与其他研究结果进行对比，将其量纲为一后ε∗=(εb0)1/3/w0。大气湍流速度场生成后，将其插值到尾涡计算域上。本文选取湍动能耗散率ε*=0.05来表示中等强度湍流（能谱如图2 所示），作为降雨条件下尾涡演化的背景大气环境。

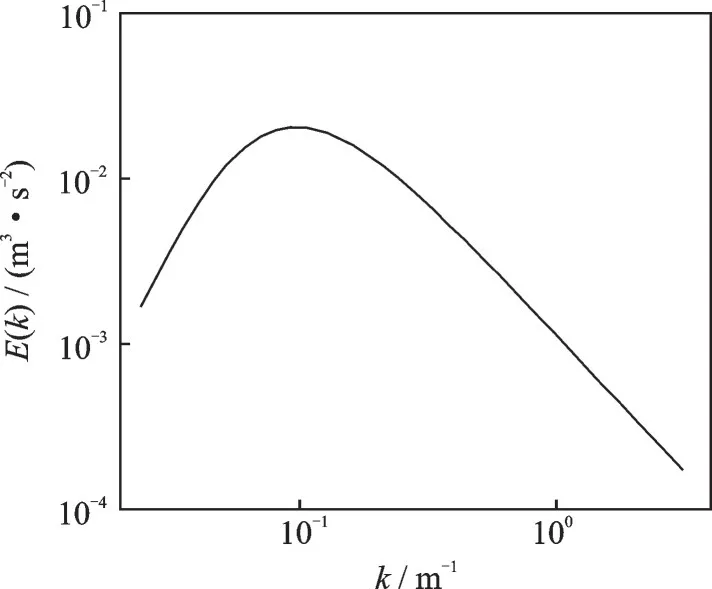
图2 ε∗=0.05 大气湍流初始能谱Fig.2 Energy spectrum of ambient turbulence for ε*=0.05

2.3 雨相初始与边界条件

雨滴在下降过程中，受到自身重力和空气阻力的作用，当下落雨滴速度增加到一定水平时，重力与阻力平衡，这时雨滴可认为是匀速运动。对于本文给定的雨滴直径D=0.5 mm，其最终速度可由以下经验公式计算[15]。

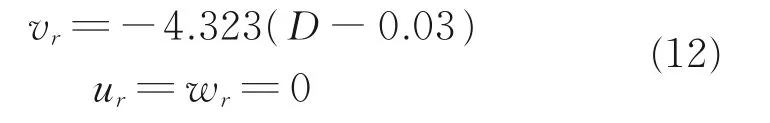
将此作为雨相的速度初始值。

雨相的初始体积分数由以下公式计算。

式中：R 为降雨率，本文取3 个等级的降雨强度，分别为R=0，5，10 mm/h；f 为某一直径的雨滴占总雨滴数的比例，由于本文选取了雨滴直径均数，故f=1。

选 取 计 算 域 尺 寸Lx×Ly×Lz=8.5b0×8.3b0×12.4b0，其中x，y 和z 分别表示飞行方向、展向和垂直方向。3 个方向的网格尺寸均为Δ=0.5 m，涡核半径与网格尺寸的比值rc0/Δ=6。需要注意的是，由于大气湍流场的生成网格与尾涡演化计算网格的尺寸不同，需将前者的速度场插值到后者的网格上。由于尾涡演化中会产生Crow 不稳定性变形，其变形波长约为8b0，因此飞行方向尺寸8.5b0是足够的。对于空气相，计算域的顶部和底部采用零梯度边界条件，即∂(u,v,w)/∂z=0，其他边界采用周期边界条件。而雨相的上边界给定速度入口，其值为前文的雨滴最终速度，下边界为零梯度边界，即∂(ur,vr,wr)/∂z=0，其他边界与空气相相同。空间和时间离散分别采用中心差分格式和二阶迎风格式，计算时间步长取0.01 s，保证CFL（Cou-rant number）数小于0.5。

3 降雨条件下的尾涡演化分析

为了分析网格对尾涡耗散的影响，设计了5 个不同网格尺寸的二维大涡模拟算例，主要考察尾涡的切向速度对网格的敏感性。5 个算例的涡核半径内包含的网格数分别为rc0/Δ=2.5，5，6，10 和12，其中rc0/Δ=6 为本文研究降雨条件尾涡演化的网格分辨率。图3 显示了t*=1 时刻尾涡的切向速度分布。可以看到，网格分辨率rc0/Δ=2.5 产生很大的数值耗散，切向速度峰值下降到了初值的57%。网格分辨率rc0/Δ=6 的峰值为0.95，而当网格尺寸进一步减小时，网格数值耗散不再明显下降，说明本文采用的网格分辨率足够，同时也没有过度的提高计算成本。

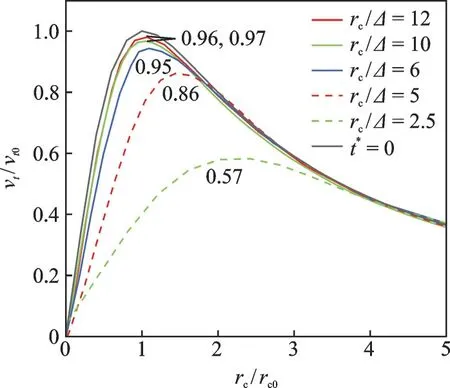
图3 t*=1 时二维算例不同网格分辨率的切线速度Fig.3 Tangential velocity of two-dimensional cases under different gird sizes for t*=1

在干净大气中，尾涡的演化与耗散可分为两个阶段[16]，在尾涡形成与发展的初期，其强度的衰减较慢，尾涡基本处在直涡或微小变形阶段，而在其发展的第2 阶段，尾涡由于Crow 长波不稳定性出现严重的变形，其强度也迅速减弱，直涡逐渐发展为涡环。

本文首先计算了无降雨条件（即R=0 mm/h）的尾涡演化情况。在计算中，包含雨相的两个方程（式（5）和（6）），但给定一个极小的雨相体积分数ar。虽然此时是无降雨情况，但这里如果不考虑雨相方程，只计算空气相的大涡模拟方程，或是给定雨相体积分数为0，是无法评估文本多相流方程的合理性的。本文计算了3 个不同大气湍流度、R=0 mm/h 条件下尾涡演化情况，图4 显示了中等强度（ε*=0.05）和高强度（ε*=0.23）大气湍流下的尾涡结构。

尾涡的环量反应了其强度。这里环量的计算方法是取11 个圆面（以涡心为圆心，半径为5～15 m）涡量的面积分的平均值，积分涡量的方向为前机飞行方向，再用t=0 时刻的初始环量对其量纲为一[17]

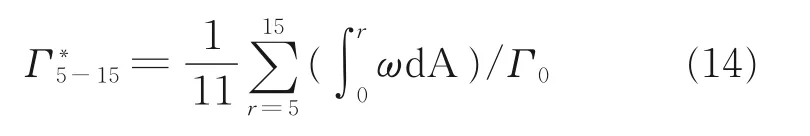
图5 为尾涡环量随量纲为一时间（t*=t/t0）的演化，可以看到不同的背景大气湍流强度对初期尾涡耗散速率几乎没有影响，而对尾涡进入快速耗散的时间影响明显，该时间随湍流度的增大而减小。通过与文献[3]基于单相流的尾涡环量演化结果对比，可以看出本文结果与其吻合较好。

为了进一步验证本文结果的可靠性，本文采用了雷达回波模型来计算尾涡中雨滴的回波信号来与雷达观测结果对比，模型表达式为

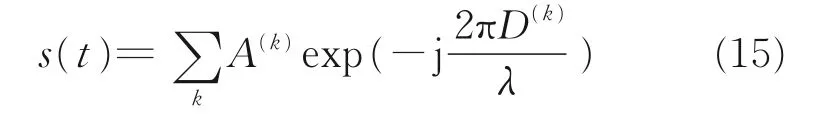
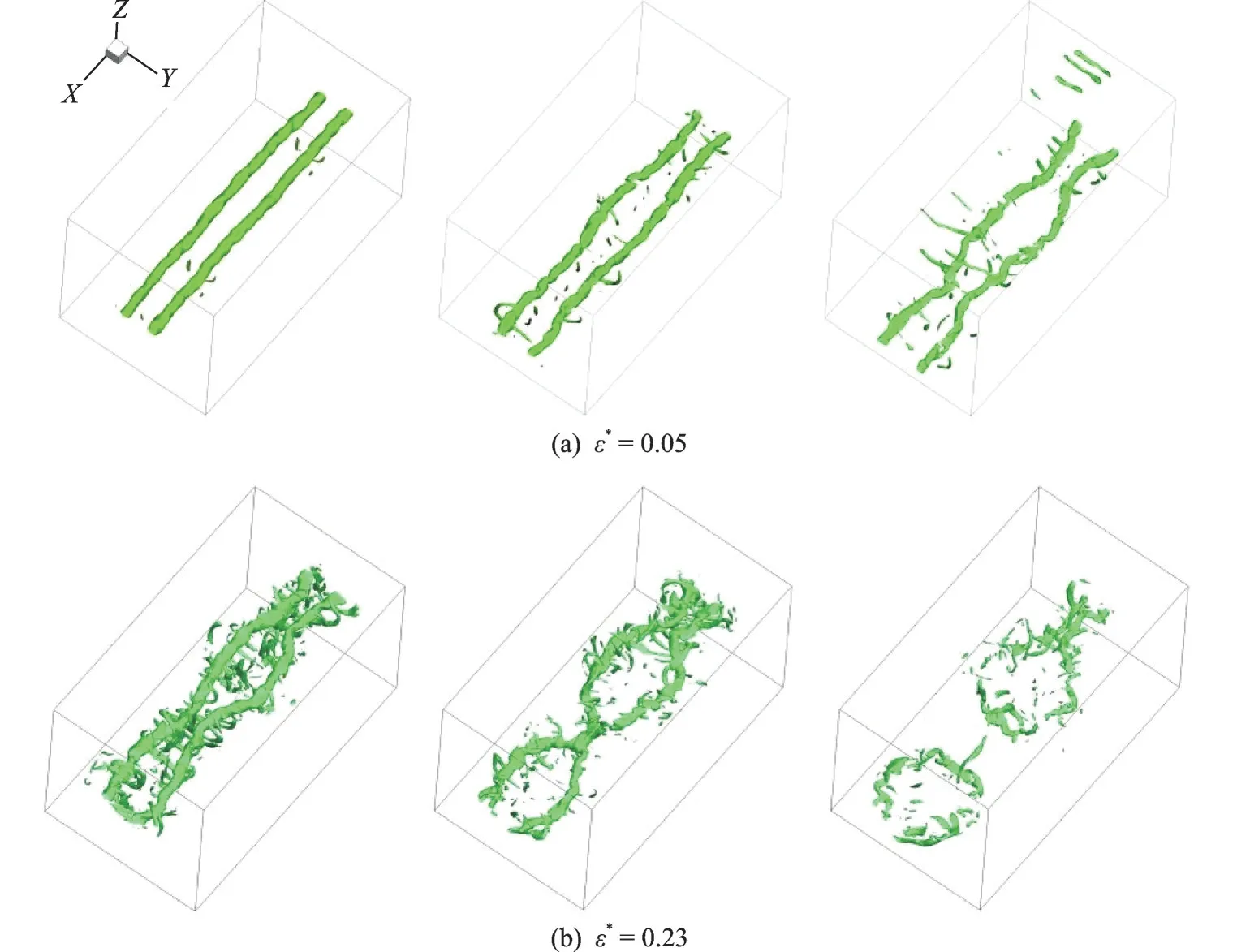
图4 涡量等值面ω=2/s（左：t*=3，中：t*=4，右：t*=5）Fig.4 Iso-surface of vorticity with ω=2/s (left：t*=3, middle：t*=4, right：t*=5)

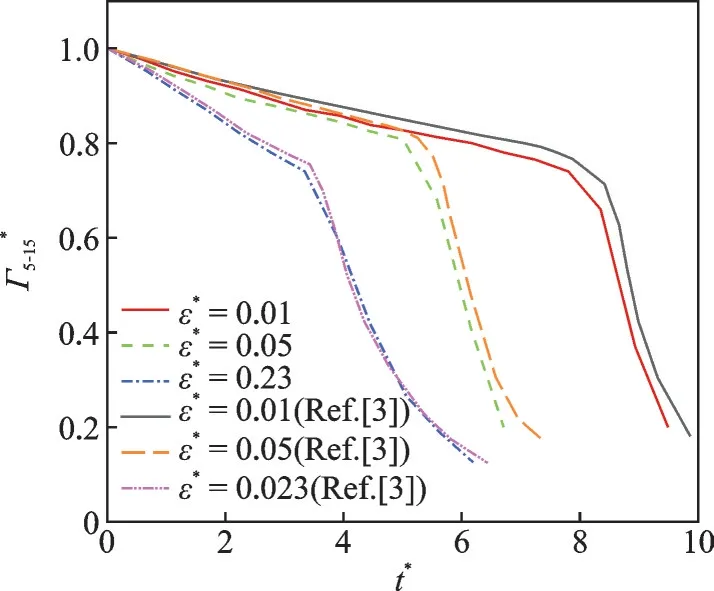
图5 降雨率R=0 mm/h 条件的环量演化Fig.5 Evolution of circulation under R=0 mm/h

式中t 为采样时间，k 为雨滴编号，由于该回波模型是基于离散的雨滴回波信号，因此在雨相插入了离散点，并根据雨相速度场进行实时更新。A 为信号幅度，D 为雨滴到雷达的距离，λ 为雷达波长。通过对256 个原始信号采样点进行傅里叶变换，得到尾涡场中雨滴的多普勒谱，如图6（a）所示。从图6 中可以读出，雨滴的多普勒宽度约为8 m/s，它反映了尾涡的速度范围。图6（b）为文献中采用X 波段雷达并经过数据处理得到A320 尾涡周围雨滴多普勒谱[6]，其中横轴为多普勒速度，纵轴为量纲为一能量，本文只呈现出了其大致趋势，将能量的幅度波动细节忽略。从图6 中可以看出，本文结果与现场观测结果的能量幅度值和多普勒速度的范围有区别，这是因为两者的量纲为一和雷达扫描方式不同，但是两者的多普勒宽度很接近，也就是尾涡的速度范围相近，说明本文方法能对雷达观测有较好的模拟效果，也证明了本文数值模拟方法的可靠性。

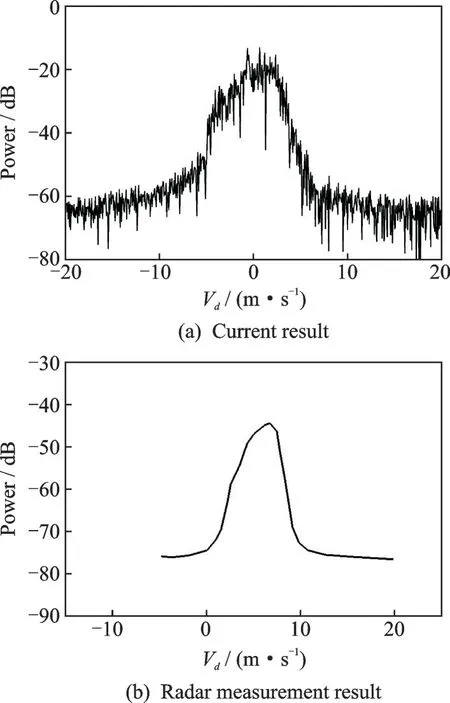
图6 本文模拟与雷达观测的多普勒谱对比。Fig.6 Comparison of Doppler spectrum between simulation and radar measurement

对于有降雨的情况（即R=5 mm/h 和10 mm/h），本文设定了中等强度的大气湍流条件。图7 为3 个降雨率条件下尾涡环量随时间的演化。可以看到，降雨率的不同影响尾涡进入快速耗散阶段的时间，降雨率越大，尾涡的耗散越快。这是由于空气相通过拖拽力源相将能量传递给雨相，体积分数越大，能量的传递越多，使得尾涡更容易失稳变形。然而，由于雨滴在空气中的体积分数很小，能量的交换是有限的，这使得降雨率对尾涡耗散的影响小于大气湍流。图7 中显示，降雨率R=10 mm和5 mm 条件下尾涡的快速耗散开始时间比无降雨情况大约提前了0.5 和1 个量纲为一时间，尾涡强度耗散到后机可承受程度的时间也就缩短了相应的时间。通过量纲为一时间可以将这个趋势扩展到其他机型，机型越大，缩减的时间越长。这说明，在降雨条件下的机场尾流间隔可根据降雨率的大小与前后机组合作适当调整。图8 显示了t*=5时不同降雨率下的涡旋结构，由2/s 的涡量等值面显示。可见，雨中尾涡的不稳定性演化与晴空中相同，都是从直涡到变形涡再到涡环的过程。但是由于降雨的影响，尾涡的变形和连接比干净大气要早，尾涡的快速耗散是从涡对的连接开始，因此这一结论与尾涡环量的演化是一致的。

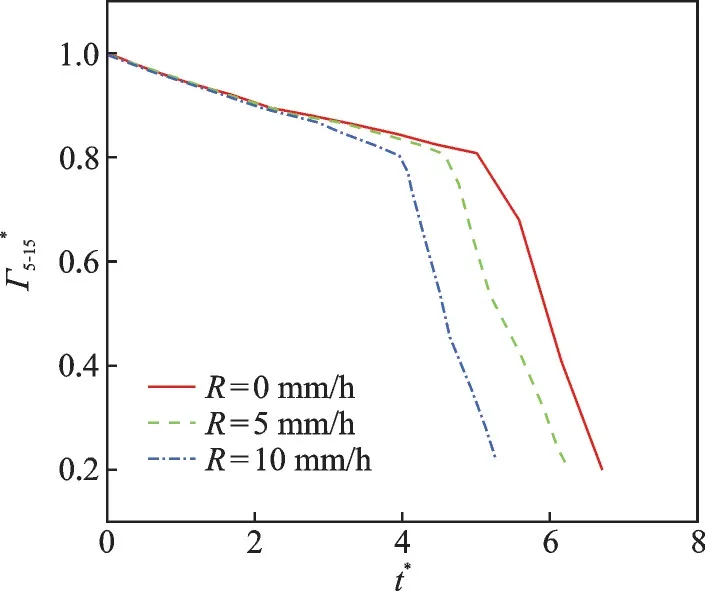
图7 不同降雨率下的环量演化Fig.7 Evolution of circulation under different rainfall rates

图8 ε*=0.05、t*=5 时不同降雨率的尾涡结构Fig.8 Vortex structure under different rainfall rates with ε*=0.05 at t*=5

图9 为t*=1.5 时刻不同降雨率对量纲为一涡量的影响。可以看到随着降雨率的增大，涡核的高涡量区域在减小。对于无降雨情况，左涡核的最大量纲为一涡量为140.2；降雨率为R=5 mm/h 时，最大量纲为一涡量为136；降雨率R=10 mm/h 时，最大量纲为一涡量减小到了129.8，这也再次说明了雨相的存在消耗量尾涡能量，削弱了其的旋转趋势，从而加速了尾涡的耗散。同时还可以从图9 注意到，由于降雨的影响，尾涡位置也有所不同：降雨率越大，尾涡下降越快，这是由于雨相的最终速度是向下的，给予尾涡一个向下的拖拽力，使得尾涡加快下沉。

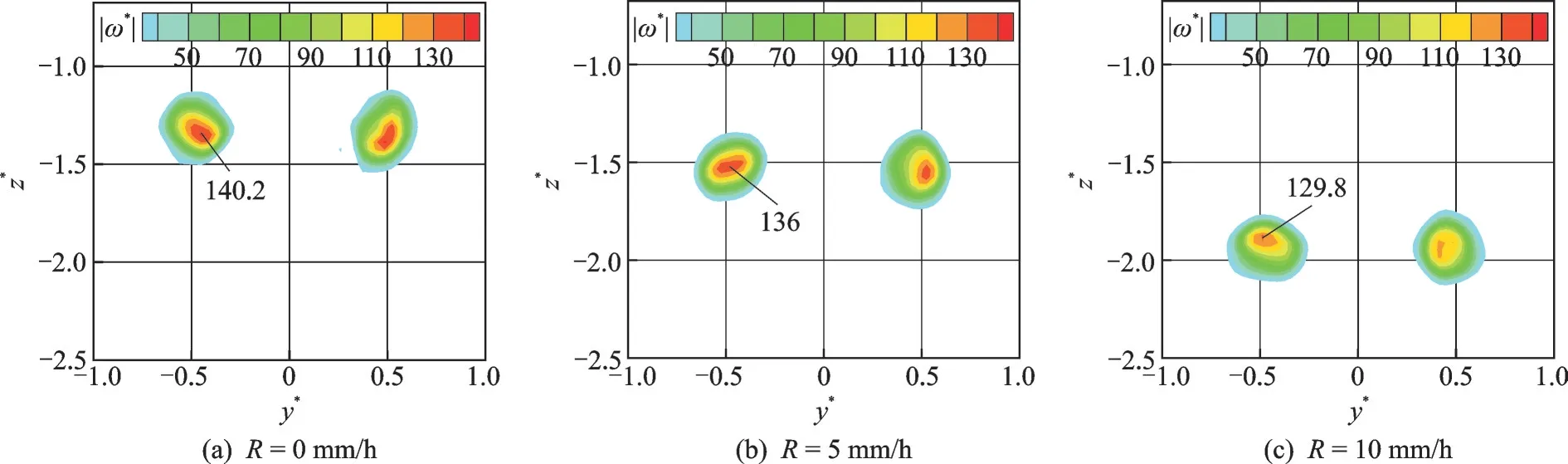
图9 t*=1.5 时刻3 个降雨率下的涡量|ω*|=|ωt0|分布Fig.9 Vorticity distribution under different rainfall rates at t*=1.5 (|ω*|=|ωt0|)

降雨率导致涡核处涡量减小，也可以从速度分布直观地看出。图10 为3 个降雨率的涡核处的垂直速度分布。图10 中显示降雨使得速度峰值下降，R=10 mm/h 情况的变化尤其明显，速度峰值较无降雨减少了约1/3。可见，与大气湍流一样，雨相的存在对涡核区域的速度分布有“抹平”作用，使尾涡加速耗散。这种现象产生可由动量方程中的源项解释，其中的空气相与雨相间的速度差(ui-ur)是主要原因。雨滴的自由下落被尾涡扰动，这时两相在距离涡心一个涡核半径位置的的速度差最大，而向靠近和远离涡心的两个方向速度差逐渐减小，速度差越大，雨相施加在空气相上的拖拽力越大，因此，速度峰值下降明显。这个作用与大气湍流产生的耗散机理不同，后者是将扰动或是涡量注入到尾涡中，使尾涡产生长波或短波不稳定性，涡结构的变形和二次涡加速了其耗散。

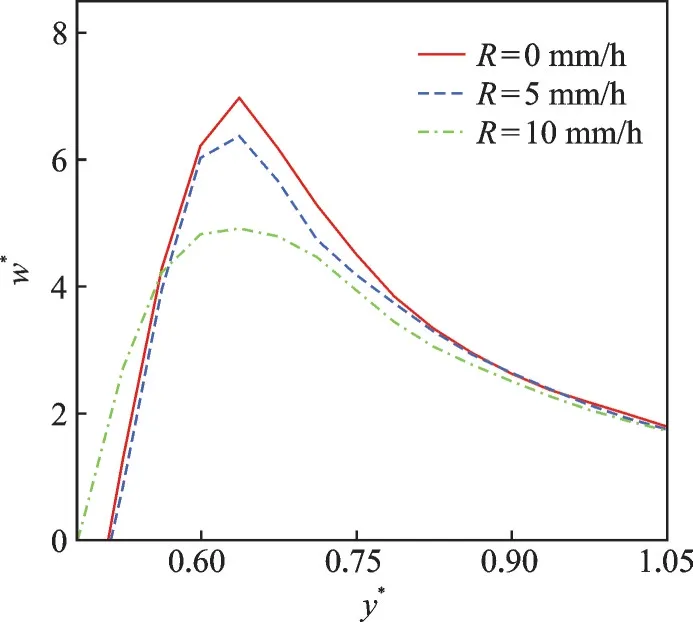
图10 t*=1.5 时刻涡核高度的垂直速度分量Fig.10 Vertical velocity component at t*=1.5

图11 为各降雨率下尾涡的下降情况。与预想情况一样，降雨率越大，尾涡下降地越快。由于本文在R=5 mm 和10 mm 选取了相同雨滴直径均数，使得两者有相同的最终速度，因此两个降雨率的初始速度差（t*=0 是两相速度的差）也基本一致，但体积分数是不同的，这也使不同降雨率情况对空气相的拖拽作用是有区别的。雨相输运方程中的重力源项提供了速度势，由拖拽力源项与空气相产生动量交换。雨相对尾涡下降的影响也与大气湍流的作用方式不同：在扩散阶段，尾涡在不同强度的大气湍流下基本能保持同一速度，即初始下降速度w0，而降雨改变了尾涡这一下降规律。在降雨条件下（中、小雨率），由于雨滴体积分数很小，不足以与尾涡产生大的动量交换，尾涡仍保持两相演化特征。降雨率的大小影响动量的交换。降雨率或体积分数越大，雨滴的有效密度越大，对尾涡的拖拽作用越强。降雨加速了尾涡的下降，这可能使尾涡危险区域（超过后机可承受的滚转力矩）更早地脱离后机的飞行廊道，减少后机遭遇高强度尾涡的风险。

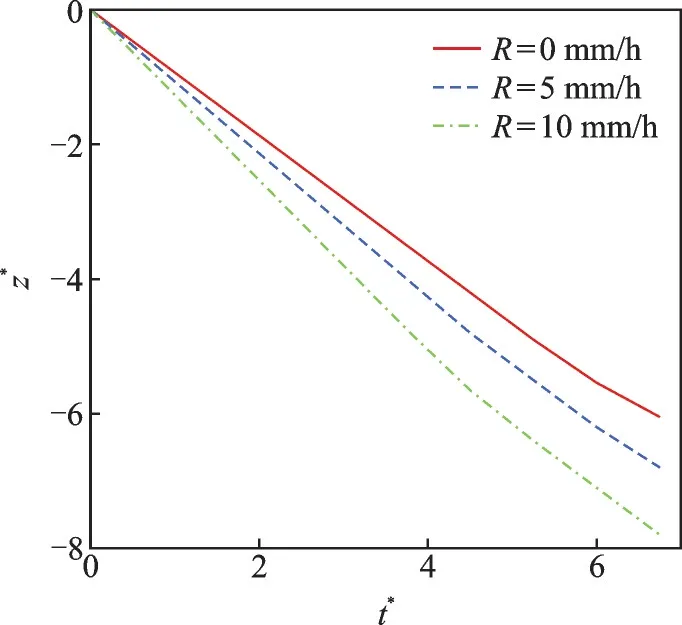
图11 尾涡的下降Fig.11 Wake vortex descent

由于雨滴对尾涡的跟随特性，尾涡的强度和位置对雨滴的运动轨迹和速度有很大的影响。因此，雨滴的运动可以反映尾涡的主要特征，雨滴的响应可以进一步用于反演尾涡环量。图12 显示了两个降雨量雨相体积分数及其流线。在本研究中，降雨被视为连续相，因此这些流线可视为雨滴的轨迹。如图12 所示，尾涡场对雨滴的运动轨迹有显著影响。轨迹在形状和密度上都发生了变化，这导致了雨滴浓度和速度的改变。尾涡存在使雨滴的分布受到干扰，不同区域有着不同的雨滴的浓度。在涡核的斜下方区域，由于穿过该区域的雨滴较少，雨滴浓度降低，但是在两个涡核之间的区域，由于汇聚作用，浓度增加。但同时也注意到，两个降雨率在涡核位置有着几乎相同的浓度。在对尾涡的雷达观测中，雨滴浓度的变化会影响局部区域的反射率。此外，由于雨滴的跟随性，雨滴的速度与涡核附近的尾涡速度近似相等，雨滴浓度和速度特性将反映在雷达信号中，这将使雷达信号的多普勒宽度增加（从前文采用雷达模型得到多普勒谱可以看到），可以间接地监控尾涡强度。

4 结 论

在进近阶段，飞机遭遇高强度的尾涡会导致其难以着陆和复飞等后果。对尾涡强度的精确评估尤为重要，雷达观测是监测尾涡的有效手段。降雨条件下，雨滴的强散射特性有利于雷达观测尾涡。数值模拟可以方便地建立降雨率与尾涡强度的关系，为尾涡的雷达观测提供理论支持。本文采用欧拉-欧拉多相模型模拟了降雨条件下尾涡的演化过程。空气相的模拟采用大涡模拟湍流模型，对于雨相，通过两个标量方程控制其动力学输运，两相间的耦合利用动量源项实现能量的传递。通过给定一个极小的体积分数来研究无降雨条件下尾涡的演化特征并与先前研究结果对比，验证了此多相流模型和数值方法的准确性。本文研究了中等大气强度（ε*=0.05）、降雨率为R=0，5，10 mm/h 条件下尾涡的演化特性。研究得到了以下结论：

（1）与欧拉-拉格朗日多相流模型相比，该模型考虑了雨滴动力学对尾涡演化的影响，可以更直接地控制降雨的初始条件和边界条件。

（2）降雨率R=5 mm/h 和10 mm/h 的快速耗散开始时间较无降雨情况的分别提前了0.5 和1 个量纲为一时间，说明降雨加速了尾涡环量的衰减。

（3）降雨削弱了尾涡的旋转趋势，使得涡核区域的最大涡量减小。雨相对涡核附近的速度梯度有“抹平”作用，R=10 mm/h 情况的速度峰值较无降雨条件减少了约1/3。

（4）降雨改变了尾涡扩散阶段的下降规律，使得初始下降速度大于w0。

（5）尾涡也影响了雨滴的运动轨迹和浓度，雨滴在涡核与其斜下方位置分散，在涡核正下方汇聚。

以上结论说明，降雨与尾涡存在运动上的耦合效应，降雨率与尾涡强度具有相关性。降雨气象条件下，尾涡强度被削弱，降低了尾涡遭遇的危险性，提高了着陆飞机的飞行安全性。