基于遗传算法的电力企业仓库货位分配优化

叶可欣，周 靖

（1.新乡学院管理学院，河南 新乡 453003；2.国网新源水电有限公司新安江水力发电厂，浙江 杭州 311608）

0 引言

随着电力企业生产规模的不断扩大，传统模式下的仓库管理模式由于利用率较低等问题已经不能很好地胜任电力企业仓储管理的需要[1]。自动化立体仓库又称为自动仓储，极大地提高了物流整体运行效率，在物流活动中有着举足轻重的地位[2-4]。对货位进行有效分配至关重要，合理的拣选路径可以节约时间、提高效率、同时降低拣选过程中设备所消耗的能量，进而降低成本。

货位分配就是考虑货物货架的实际性质，给出入库货物分配合理储位，达到仓储利益最大化的目的。文献[6]以仓储用途为标准进行区位划分，将仓库分为5大区模块；文献[7]利用不同的仓库水平位置，按照货物流通速度、出入库频率高低划分区位；文献[8]将仓库入料作为参数，建立数学模型用来寻取最优货位；文献[9]在研究不规则空间的自动仓库系统货物分配策略的基础上，构建了货位优化的数学模型。文献[10]在研究仓库信息化、现代化的过程中，引入了自动化分配的概念，将建模指标确定为货位的动态分配

本研究基于某电力企业立体仓库，将货物出入库效率、存储货物之间的相关性以及保证货架的稳定性作为优化目标进行研究，建立货位分配的优化模型，并引入多目标遗传算法对优化模型进行求解，从而能有效提高仓库作业效率。

1 自动化仓库货位分配优化

1.1 模型假设

货位分配就是考虑货物、货架的实际性质、货物出入库频率等因素，给出入库货物分配合理储位，以降低仓储作业成本，从而达到仓储利益最大化的目的。

货物入库和出库的分配主要分为两种情况：入库时的货位分配和出库时货位的选择分配。前者根据入库的货物情况选择适当数目的货位进行摆放，后者根据出库的货物情况，将不同位置的同类货物进行出库操作。仓储过程中货物的合理分配一般遵循以下几个原则：

（1）先入先出原则。同一种类型的货物必须满足先进入仓库的要先出库这一原则，这样才可以减少货物在仓库中积压的时间，并安排入库频率高的货物置于离出入库口较近的货位，从而使货物的存储更加方便，让货物出入库的效率得到普遍的提高。

（2）稳定性原则。即将货物合理均匀分配在货架上，轻物安放在货架的上层，重物放置在货架的下层，实现货架“上轻下重”，从而保证货架稳定性。

（3）相关性安放原则。若货物之间存在一定的相关性，把需要同时出库的货物将其放在相近或是相邻的货位。考虑货物自身的性质应谨慎安排货位，如特殊类型货物要放在特殊的位置并且尽量安放在一起。

根据某电力企业仓库实际情况，进行模型简化。描述如下：假设在某个仓库区域中，该仓库共有a排立体货架，且每排为b列c层。因此，位于第ak排bk层ck列的货架可表示为：(ak，bk，ck)（ak=1，2，…，a；bk=1，2，…，b；ck=1，2，…，c），坐标（0,0,0）表示仓库的入口。图1为本研究货架俯视效果图。

图1 货架俯视效果图

从货架俯视图中可以将货位进行优化，针对此问题作以下假设：

（1）已知每种零件存放的种类，并且相同体积的容器其质量分布均匀；

（2）每种零部件的周转率已知；

（3）一种零部件对应一个货位；

（4）立体仓库采用单端出入库方式；

（5）每种货位单元格的长宽高以及巷道宽度均为定值l0；

（6）仅考虑拣选时间，不考虑零部件存取耗费的时间。

1.2 参数定义

根据假设，(a，b，c)：货架共有a排、b列、c层；(x，y，z)：货物在第x排，第y列，第z层的坐标；Vx：堆垛机在巷道上取送相应货物水平方向的平均速度；Vy：堆垛机沿另一水平方向的平均移动速度；Vz：堆垛机沿垂直方向的平均移动速度；l0：长度、宽度、高度相同的货架单元格；n：所有货物共n类；k：货位上存放的是第k类货品；pk：第k类货品的周转率；mk：第k类货品的质量；nxyzk：k在每个货位的取值不定；nxyz：存储在(x，y，z)货位坐标上的第k类货物的数量。

2 多目标优化的数学模型

2.1 出入库周转效率分析

在仓储管理的时候，必须要对每一个入库的货品进行严格地检查，执行严格的出入库管理。实际货物物流的过程中，每天都会有大量的货物进出仓库，因此合理利用好仓库空间，协调好管理人员之间的关系，提升货物出入库效率是仓储管理中急需解决的一个问题。想要提升货物出入库的效率，首先就要把时间作为一个重要的考虑因素：将货物出入库的实际时间作为衡量标准，推算出货物出入库位置合理的距离公式。

在现代的仓储管理中，货品上架和下架基本都是由堆垛机完成的，而堆垛机在竖直方向和水平方向上移动速度是不同的。对于大部分仓库而言，堆垛机的速度大致是差不多的，尽管堆垛机在实际独立取送货物中有着x轴和y轴两个不同的速度，但是它们的平均速度大致相同。假设（xk，yk，zk）是货位的坐标，用k表示摆放在货位的第k类货品，那么X，Y，Z方向上的移动平均速度表示为Vx，Vy，Vz，l0为货架单元格长宽高，并且都是已知的常量，假设堆垛机3个方向的平均速度Vx、Vy、Vz是不变的，可以推导出提高出入库效率模型公式：

2.2 出入库稳定性分析

重心低的物体具有较好的稳定性，为了降低货架的重心，将货品按照“上轻下重”的原则放置，以此来增强货架的稳定性。将货架的重心设置为第二个计算因子，将货架的重心降到最低就是货物摆放所要达到的最优目标。

根据排列层的样式，首先设计仓库货架布局，计算每排每列货架的重心。为了求取整个货架重心的最优解，首先需将每排的所有列进行加权，然后再将所有排整体求和。对该目标函数进行推导，得到货架中心。整个仓库的货架稳定性函数模型如下：

2.3 货品种类分析

要实现仓储管理的现代化，就必须使仓库在有限的空间内放置更多的货品，在探求货品存放最优模式时，不仅要考虑布局仓库货位对空间的占用，还要注意货品摆放的序列。根据仓库货位放置的货品来确定第k类货品（ak，bk，ck）中心坐标位置。根据不同实际情形，建立单独的目标函数模型。联立后如式（3）所示：

式中，每个货位单元格的长度l0，第k类（k∈[1，n]）货品的周转率pk，第k类货品的质量mk，货位分类存放时第k类货品的中心点坐标为（ak，bk，ck），该坐标第k类货品的存放数nabck。

3 货位优化的多目标遗传算法实现

本文基于多目标遗传算法建立一系列效用函数与目标函数之间的相关联系，借助效用函数关联多个目标，在效用函数的协调下，使得多目标优化向单目标优化转化，便于最优化运算求解[12，13]。对于货物优化问题，可将货物坐标标识为基因，染色体即为货物坐标的排序序列，多条染色体可组成一组有效种群解，从而在种群基础上搜寻多目标规划问题的最优解。

3.1 货位算法编码

根据实际仓库情况，货架的排和列数小于32，层数小于8。对货位的编码：货位编号由6位数组成，编号是从010101到323208，仓库货位前面两位编号表示排，中间两位编号表示列，最后两位编号表示层，这种编号前两位和中间两位阿拉伯数字不能超过32，最后两位不能超过8。编号编码表如表1所示。

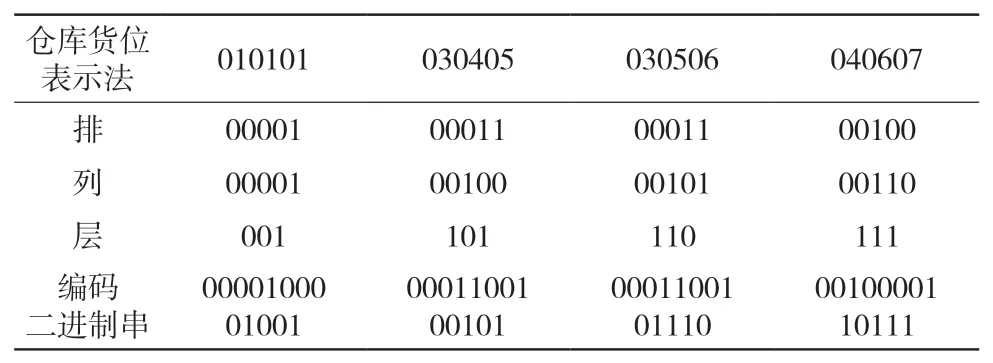
表1 货位编号

实际操作中，需要按照不同的编码方法进行编码，同时又想把不同编码方法得到的参数结果连接在一起，则常要在GA编码方式中利用参数级联编码方式，目的是在不改变原来编码的基础上依次将它们按照顺序连在一起，从而得到整个参数的编码。综上分析采用5∶5∶3编码方式对参数解码。解码过程顾名思义则将其按照5∶5∶3这样比例进行拆分开来，例如二进制编码串为X:1000101111100，可以将二进制编码串拆分成3个子串，并分别将3个子串进行解码：10001转换为十进制是X1=16+1=17；01111转换为十进制是X2=8+4+2+1=15；100转换为十进制是X3=04。因此，可以求出二进制编码解码为(171504)。

3.2 初始化种群

在进行货位优化方面，首先考虑初始种群的设定，因此在整个仓库中，货位和货物是相互对应的关系。一旦货位确定下来，货物的位置也就相应的确定下来。在用二进制编码时，就不用担心生成的是不是0或1，仓库中总会使货物与货位有着匹配的关系，然后将每个产生的货位编号连接起来即可构成一个初始个体。为了更加合理有效地对货位进行分配，在盘点一些短期或长期储存的货物时要尽可能的采用货位优化方式，更要在货物刚要入库上架的时候运用进来。

4 实例仿真验证与结果分析

4.1 仿真参数设定

基于某实际仓库算例，具体需要优化的数据参数如表2进行设定，利用MATLAB程序对货位进行分配优化。表2中的参数建立在仓库2排6列4层分类的固定货架，在它的基础上，分别设置了水平方向和垂直方向的恒定速度，单位长度为定值的货架。通过初步设置以及接下来的数据样本导入，为整个货位分配优化及仿真运行提供了准备。

表2 优化仿真参数

对于不同类货物单位质量、仓库存货数量，可以在企业物资部门出入库订单信息中查询到。零部件的周转率是通过数据计算得到的，即现有仓库样本存量与初始入库样本量的比值。由于上述中涉及到货物之间的相关性，需要对货位的中心坐标进行设定，表3给出了初始存储货位坐标和中心坐标零部件初始数据。

表3 待优化零部件初始数据

4.2 仿真结果分析及模型验证

仿真结果分析：选取零部件重量和周转率作为数据样本，在优化过程中将周转率数据以百分百数值代入优化程序，如周转率为0.56的零部件实际代入优化求解程序的数值为56。运用MATLAB对程序进行优化处理，其结果追踪如图2所示：

图2 目标函数解结果追踪

通过目标函数仿真运行追踪解可知，目标函数在寻找最优解时，它们在收敛时的优越性是不一样的，但基本上都找到了在该领域内的优解。由于多目标优化在权重系数灵活性的变化下，通过线性组合转化为单目标优化进行求解，通过图2单目标优化追踪解比较分析，迭代次数在100以内基本上趋于稳定。

表4 目标函数值对比

从表4中可以看出，经优化后的零部件的出库效率、货架重心最低、货物相关性等性能都得到一定程度上的改善，3个目标降低率分别为：18.20%、33.46%、12.22%。

为了更加直观地观察货位优化后的实际效果，根据货位坐标，利用MATLAB模拟出优化前后货位分配状态的三维模拟图，图3为优化前后的货位分配状态。

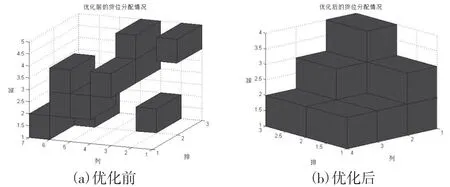
图3 优化前后货位分配状态

对优化前后的货位分配状态进行对比发现：货位进行优化前，优化区域内的货位分配杂乱无序，布局不合理，经过货位优化后，货位的分配都尽可能地靠近仓库出入口和货架低层，货位分配的布局变得有序合理，这就使得货位分配方案在满足提高零部件出库效率的基础上，降低了货架的重心，提高了货架的稳定性。

5 结束语

针对物资仓库存在的诸多实际问题，基于某电力企业仓库实际情况，进行货位分配模型建模与优化算法设计，建立了货位分配优化模型并引入相应的算法和改善的算法。根据货位多目标优化模型实际需要，采用改变权重系数来解决该问题。最后利用MATLAB软件验证经过优化后的货位模型具有较好的适用性和合理性，充分证明了本研究优化策略的可靠性。