船舶动力设备拆装过程的网络模型及复杂性分析

陈登智　江国和　孙久航　刘婵娟

摘要：

船舶动力设备拆装是船员适任证书考试的重要环节，为对该考试过程进行智能化评估，将船舶动力设备拆装过程抽象为以拆装任务为节点、任务之间联系为边的复杂网络。从网络整体结构特征和局部特征两个方面对网络复杂性进行分析;通过测量网络节点中心性指标对设备拆装关键任务进行识别;通过计算网络最短路径进行任务相关性分析，确定设备拆装的步骤。以船用6135柴油机吊缸拆卸过程为例，验证了模型的有效性。本文提出的方法还可为其他机械设备的拆装和维修过程提供参考。

关键词：

船舶动力设备; 虚拟拆装; 复杂网络; 中心性指标; 复杂性分析

中图分类号：  U664.12

文献标志码：  A

收稿日期： 2020-06-01

修回日期： 2020-12-16

基金项目： 国家自然科学基金（11571008）;上海海事大学研究生创新基金（2015ycx076）

作者简介：

陈登智（1980—），男，湖南衡阳人，助理研究员，博士研究生，研究方向为船舶动力设备拆装过程建模和智能优化，

（E-mail）dzhchen@shmtu.edu.cn;

江国和（1963—） ，男，江西都昌人，教授，博导，博士，研究方向为动力机械振动噪声控制，（E-mail）ghjiang@shmtu.edu.cn

Network model and complexity analysis of disassembly and assembly process of marine power equipments

CHEN Dengzhia， JIANG Guohea， SUN Jiuhanga， LIU Chanjuanb

（a. Merchant Marine College; b. Institute of Logistics Science & Engineering， Shanghai Maritime University， Shanghai 201306， China）

Abstract：

The disassembly and assembly of marine power equipments is an important link in the certificate examination of competency for seafarers. In order to evaluate the examination process intelligently， the process of disassembly and assembly of marine power equipments is abstracted into a complex network composed of nodes denoting tasks and connecting lines between tasks. The network complexity is analyzed from the overall structure characteristics and the local characteristics of the network. The key tasks are identifiedby measuring centrality indices of the network nodes. The task correlation is analyzed by calculating the network shortest path， and the process of equipment disassembly and assembly is determined. Taking the process of disassembly of the marine 6135 diesel engine cylinder as an example， the validity of the model is verified. The proposed method can provide reference for the disassembly， assembly and maintenance process of other mechanical equipments.

Key words：

marine power equipment; virtual disassembly and assembly; complex network; centrality index;complexity analysis

0 引 言

船舶動力设备拆装是船员适任证书考试的重要环节，也是轮机员实践操作技能的重要体现。然而，目前船员适任证书考试评估仍处于凭经验评估阶段。为对该考试过程进行科学、合理的评估，优化船舶动力设备拆装过程，本文结合复杂网络理论对船舶动力设备拆装过程的复杂性进行分析。

由于船舶动力设备的组成部分各有特点，且各个零部件在质量、尺寸、精度等方面存在差异，若拆装不当，会使零部件受损，造成不必要的浪费和安全事故。因此，必须对一些复杂的重要零部件进行必要的识别和标记，用以提醒在拆装过程中严防敲击和注意保护等[1]。目前，国内外学者对船舶动力设备拆装过程的研究并不多，且多采用SolidWorks模拟设备拆装过程[2-4]。侯政良等[5]提出了在SolidWorks环境下进行虚拟拆装的方法，建立了柴油机虚拟拆装平台，对某型船用柴油机的拆装过程进行了模拟。段尊雷等[6]根据实时的系统参数检测结果和隶属函数得出模糊关系矩阵，经多重模糊综合评判得出评估结果。

船舶动力设备是一个由众多零部件组装而成的复杂系统，可把每个零部件看作一个拆装任务，而每个零部件在拆装过程中的前驱、后继关系可以抽象为网络的边。因此，可以将船舶动力设备拆装过程抽象为一个以拆装任务为节点、任务之间联系为边的复杂网络。张青等[7]提出基于惯性动作捕获设备交互控制关系从而进行虚拟装配的方法，解决了高精度实时姿态信息收集问题。机械设备的拆装对设备的保养、检修、维护和延长生命周期具有重要意义[8]。制定复杂联动器械的拆装步骤需要考虑设备稳定性和零部件特征[9-10]。分析设备拆装过程的复杂性和拆装过程特征，是设计和优化拆装过程的基础[11]。

1998年在《Nature》上发表的《小世界网络的群体动力学行为》和1999年在《Science》上发表的《随机网络中标度的涌现》开启了复杂网络研究的新时代，复杂网络理论开始被广泛应用于生物学[12]、社会学、医学[13]、交通[14]等领域。对动力设备的拆装顺序及其制约关系采用网络进行建模，可以把对拆装过程复杂性的研究转换为对网络本身复杂性的研究。目前，尚未见将复杂网络应用于动力设备拆装过程的研究。

基于以上背景，本文应用复杂网络理论对船舶动力设备拆装过程的复杂性进行分析。首先构建船舶动力设备拆装过程的网络模型，分析整体网络特征，然后基于复杂网络理论的中心性指标建立设备拆装关键任务识别模型，并基于网络最短路径进行拆装任务相关性分析，以期为船舶动力设备拆装过程优化提供新的方法和思路，提高船员适任证书考试评估的科学性和准确性。

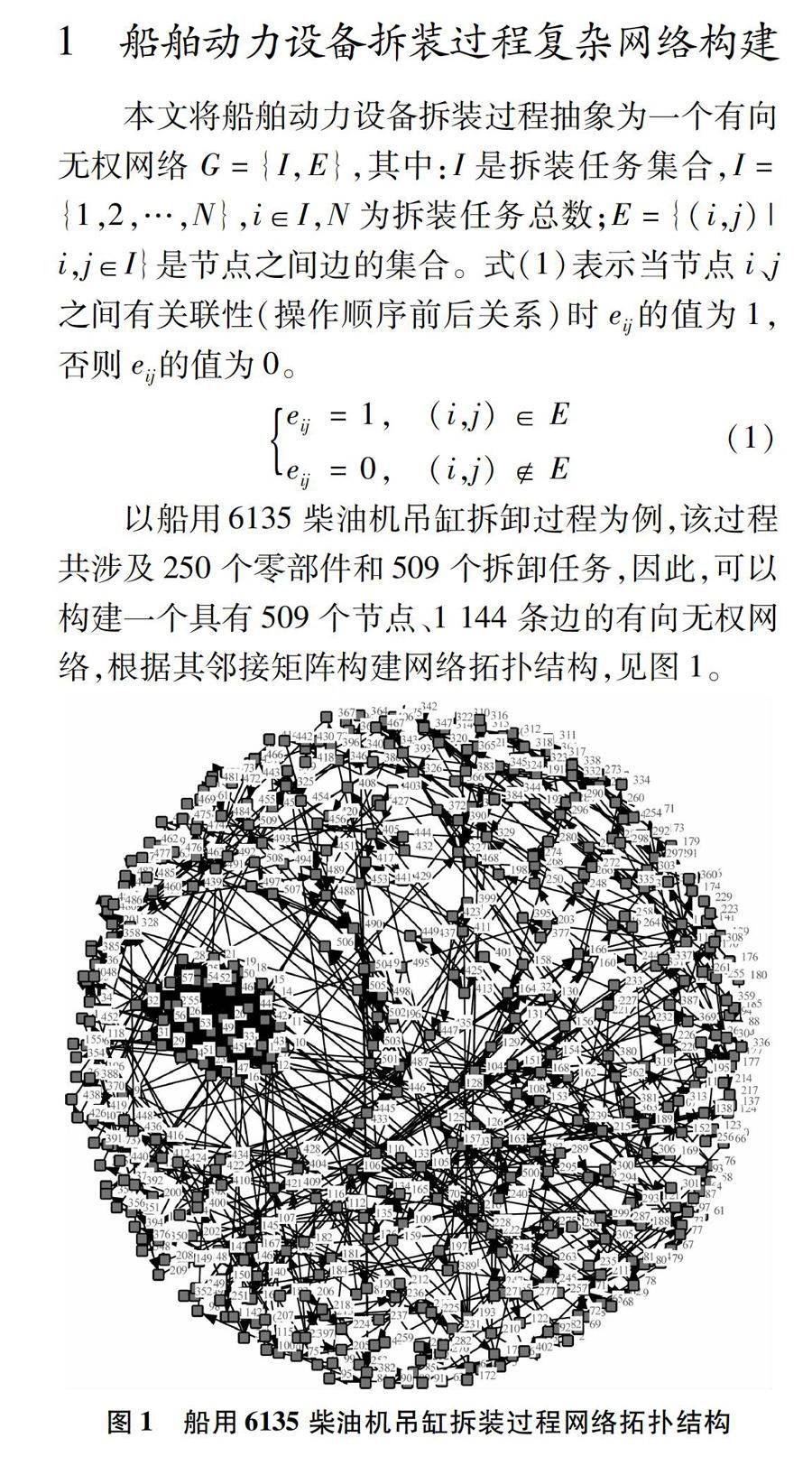
1 船舶动力设备拆装过程复杂网络构建

本文将船舶动力设备拆装过程抽象为一个有向无权网络G={I，E}，其中：I是拆装任务集合，I={1，2，…，N}，i∈I，N为拆装任务总数;E={（i，j）|i，j∈I}是节点之间边的集合。式（1）表示当节点i、j之间有关联性（操作顺序前后关系）时eij的值为1，否则eij的值为0。

eij=1， （i，j）∈E

eij=0， （i，j）E

（1）

以船用6135柴油机吊缸拆卸过程为例，该过程共涉及250个零部件和509个拆卸任务，因此，可以构建一个具有509个节点、1 144条边的有向无权网络，根据其邻接矩阵构建网络拓扑结构，见图1。

2 网络整体结构分析

在社会网络理论中，网络整体结构或多或少会对其中行动者的行为产生影响，即“社会结构”影响“能动作用”。根据船舶动力设备拆装任务之间的关系计算整体网络密度、网络聚集系数和网络平均最短路径。

整体网络密度。网络密度反映网络节点之间的联系程度，网络密度越大，表明网络节点之间的联系越紧密。在一个有向网络中，若网络节点数为N，那么这些节点之间包含的关系总数在理论上的最大值为N（N-1）/2，若网络中包含的实际关系数为M，那么整体网络密度就是“实际关系数”除以“理论上的最大关系数”：

D=2M/（N（N-1））

（2）

网络聚集系数。节点聚集系数c（i）表示该节点与其邻接节点之间的紧密程度;k表示节点i的度;T（i）表示节点i的k个邻接节点之间可能形成的最大连接边数;E（i）表示节点i的k个邻接节点之间的实际连接边数;整个网络的聚集系数c（s）为网络中所有节点的聚集系数的平均值。相关计算式如下：

c（i）=E（i）/T（i）（3）

T（i）=k（k-1）/2（4）

c（s）=Ni=1c（i）/N（5）

网络平均最短路径。任意两个节点i、j之间的最短路径用其所包含的边数dij来衡量。整个网络的平均最短路径L为网络中所有节点对之间最短路径的平均数：

L=2N（N-1）i≥jdij

（6）

计算结果显示：该网络的整体网络密度（0.004）较小，说明它是一个稀疏网络;各任务之间的集聚性较低（网络聚集系数为0.073），表明各任务之间互相影响的可能性较小，绝大多数任务具有一定的相对独立性;该网络的平均最短路径约为7.034，说明任意两个任务之間经过约7个任务的链接就会产生间接影响。

3 基于网络节点中心性指标的设备拆装关键任务识别

中心性是社会网络分析的研究重点之一，一般衡量网络节点中心性的指标有度数中心性、接近中心性、中介中心性、特征向量中心性等。本文构建的船舶动力设备拆装过程网络为一个有向无权网络，因此，选取FREEMAN[15]提出的度数中心性、接近中心性和中介中心性指标对网络节点特征进行分析，用以识别船舶动力设备拆装过程中的关键任务。

3.1 度数中心性

节点i的度数中心性指与节点i直接相连的节点的个数，可以直观反映该节点与网络中其他节点发生直接联系的可能性大小。出度kouti指从节点i指向的其他节点的个数，入度kini指从其他节点指向节点i的节点的个数，其计算公式为

kouti=jeij（7）

kini=jeji（8）

3.1.1 出度

节点i的出度反映该节点对其他节点的影响程度。图2为6135柴油机吊缸拆卸过程中各任务的出度计算结果和出度概率分布。由图2a可知，网络中仅极少数节点的出度较大，大部分节点的出度都在5以下;由图2b可知，其出度服从阶段幂律分布，因此所建网络为无标度网络。

表1给出了部分拆卸任务的出度及其排名。由表1可知：任务T6（放缸套水）和T15（拆进气管）对其他任务的影响最大，其出度均为30，这说明这两个任务与其后续30个任务都有直接联系，在设备拆卸过程中，一旦这两个任务操作过程出现错误或者失败，将导致其后续30个任务也无法完成;任务T111（检查漏水、漏气和运行状况）为最后一个拆卸任务，因此其出度为0。T6和T15的拓扑结构见图3。

3.1.2 入度

节点j的入度反映该节点受其他节点影响的程度。图4为6135柴油机吊缸拆卸过程中各任务的入度计算结果和入度概率分布。由图4a可知，与出度计算结果相似，网络中仅少数节点的入度较大，大部分节点入度都在3以下;由图4b可知，其入度也服从阶段幂律分布，再次证明了所建网络为无标度网络。

表2给出了部分拆卸任务的入度及其排名。由表2可知，入度为23的任务共有15个，说明与这15个任务直接相连的前驱任务均有23个。对于这15个任务而言，不论其前驱任务（各有23个）中的哪一个任务出错或者失败，都会导致这15个任务无法完成。

3.2 接近中心性

用接近中心性衡量一个节点不受其他节点控制的程度。如果一个节点与网络中所有其他节点的距离都很近，则称该点具有较高的接近中心性。接近中心性用节点i与网络中其他节点之间的距离测度：

CPi=jdij

k

jdkj

（9）

3.2.1 出度接近中心性

表3给出了部分任务的出度接近中心性及其排名。由表3可知：任务T15和T6的出度接近中心性最大，这说明这两个任务与其他任务之间的距离最远，对其他任务的影响和控制程度最低;相反，在所有任务中有8个任务（如T110和T74.1）的出度接近中心性几乎为0，这说明他们与其他任务之间的距离极近，其他任务非常容易受到这8个任务的影响和控制。

3.2.2 入度接近中心性

表4给出了部分任务的入度接近中心性及其排名。由表4可知：任务T102（安装油头）的入度接近中心性最大，这说明其他任务与T102的距离较远，对该节点的影响和控制能力较弱;相反，在所有任务中有3个任务（T1A、T1B、T29.2）的入度接近中心性几乎为0，这说明这些任务在整个设备拆装网络中与其他任务之间的距离极近，非常容易受到其他任务的影响和控制。

3.3 中介中心性

用中介中心性C*i来衡量节点i对其他节点的控制程度，其计算式如式（10）所示，其中gjl表示节点j、l之间存在的最短路径数量，gjl（i）表示节点j、l之间存在的经过节点i的最短路径数量。

C*i=jl（gjl（i）/gjl），

j≠i， l≠i， j

（10）

表5给出了部分任务的中介中心性及其排名，其中任务T27（拆气缸盖螺丝）的中介中心性远远大于其他任务的中介中心性，说明其在网络结构中处于中介位置，在整个拆卸过程中起极其重要的作用，想要完成大部分拆卸任务都必须先完成任务T27。

3.4 各种中心性指标计算结果比较

图5为本文所选取的5种中心性指标计算结果的对比图。由图5可知，部分中心性结果的变动过程具有一致性，比如，该网络节点的入度与中介中心性的变化过程基本一致，入度高的节点也具有较高的中介中心性。

为进一步研究各种中心性指标之间的关系，对5种中心性结果进行标准化处理后，进行相关性分析，结果见图6。由图6可知：节点的入度和出度分布集中在低值区域;高出度（入度）节点的入度（出度）较低;高出度节点的入度接近中心性较低，出度接近中心性较高;节点的入度接近中心性与中介中心性负相关，当节点的入度接近中心性增加时，其中介中心性显著降低。

4 基于网络平均最短路径的拆装任务相关性分析

船舶动力设备拆装过程网络的平均最短路径越短，两个任务之间的中间环节就越少，涉及的零部件就较少，两个任务之间的关系就越紧密，任务之间的相关性就越高。通过计算网络中任意两个节点之间的最短路径得到，与节点7、33的最短路径为1的节点数最多，均为30，说明这两个节点与网络中其他节点之间的相关性最大，其子网络分别见图7和图8。

5 结 论

本文将船舶动力设备拆装过程抽象为以拆装任务为节点、拆装任务之间的联系为边的复杂网络。首先，对这个网络的整体结构进行分析发现：以船用6135柴油机吊缸拆卸过程为例所建的网络的整体网络密度较小，是一个典型的稀疏网络;该网络的聚集系数也较小，表明各任务之间的集聚性较低，各任务之间互相影响的可能性较小，绝大多数任务具有一定的相对独立性;该网络的平均最短路径约为7.034，即任意两个任务之间经过约7个任务的链接就会产生间接影响。

其次，提出基于网络节点中心性指标的设备拆装关键任务识别模型。计算结果表明，根据不同中心性指标得到的网络关键任务各不相同，出度最大的任务为T6（放缸套水）和T15（拆进气管），这两个任务在整个设备拆卸过程中拥有最多的后续任务，对其他任务的影响程度最大。在实际操作中，放缸套水和拆进气管都是进行其他操作的必要步骤，进一步验证了该结论与实际操作情况相符。入度最大的节点有15个，其入度均为23，说明这15个任务都拥有23个前驱任务，故这15个任务在整个设备拆装过程中都受相應的23个前驱任务的影响，拆卸操作难度最大。出度接近中心性最大的任务为T6 和T15，说明这两个任务与网络中其他任务之间的距离较远，因此他们对其他任务的影响和控制程度最低。入度接近中心性最大的任务为T102（安装油头），说明网络中其他任务与任务T102的距离最远，对该任务的影响和控制能力比较弱。任务T27（拆气缸盖螺丝）的中介中心性远远大于其他任务的中介中心性，说明其在网络结构中处于中介位置，在整个拆卸过程中起极其重要的作用，想要完成大部分拆卸任务都必须先完成任务T27。

最后，通过对网络最短路径分析发现，与节点7、33的最短路径为1的节点数最多，均为30。这说明这两个任务与网络中其他任务之间的相关性最大。

本文将船舶动力设备拆装过程抽象为一个网络，采用复杂网络分析研究这个网络的复杂性，以此反映拆装过程的复杂性，有别于直接研究拆装序列，是一种通过网络统计揭示拆装过程复杂性的新的尝试。因此，通过该文提出的方法，能够分析和评估拆装过程本身的复杂性。对网络节点中心性指标的分析能够识别和评价关键拆装任务对整个拆装过程的影响。下一步将进行船舶动力设备拆装过程路径智能优化。本文在实践层面有利于明晰船舶动力设备拆装实操培训的重难点，也为船员适任证书考试中关于船舶动力设备拆装项目的智能评估系统评分赋值提供依据。

参考文献：

[1]王昊， 曾鸿， 倪文利， 等. 基于虚拟现实的船舶辅机设备拆装训练系统[J]. 江苏科技大学学报（自然科学版）， 2017， 31（1）： 44-48.

[2]曾鸿， 王心红， 张均东， 等. 面向实操评估的轮机虚拟拆装考试系统开发[J]. 中国航海， 2014， 37（1）： 24-28.

[3]胡畔. 基于SolidWorks的虚拟设备拆装系统研究[J]. 软件导刊， 2011， 10（10）： 40-41.

[4]苏玉龙， 吴桂涛， 曾鸿. 内河船机电设备虚拟拆装考试系统设计与实现[J]. 大连海事大学学报， 2014， 40（2）： 101-104， 108. DOI： 10.16411/j.cnki.issn1006-7736.2014.02.023.

[5]侯政良， 张波， 刘敬. 基于VB的船舶柴油机虚拟拆装系统研究[J]. 中国水运， 2013， 13（1）： 79-80.

[6]段尊雷， 任光， 曹辉， 等. 基于遗传算法优化的虚拟机舱协作智能评估[J]. 哈尔滨工程大学学报， 2017， 38（ 4）： 514-520.

[7]张青， 郑岩， 郭庆， 等. 航空发动机设备拆装快速装配仿真研究[J]. 计算机仿真， 2018， 35（3）： 257-261.

[8]ABUZIEDH ， SENBEL H ， AWAD M ，et al.A review of advances in design for disassembly with active disassembly applications[J]. Engineering Science and Technology， an International Journal， 2020， 23： 618-624. DOI： 10.1016/j.jestch.2019.07.003 2215-0986.

[9]BEDEOUIA， HADJ R B， HAMMADI M，et al. Assembly sequence plan generation of heavy machines based on the stability criterion[J]. The International Journal of Advanced Manufacturing Technology， 2019， 102： 2745-2755. DOI： 10.1007/s00170-019-03359-0.

[10]BATTAAO， DOIGUI A， HERAGU S S，et al. Design for manufacturing and assembly/disassembly： joint design of products and production systems[J]. International Journal of Production Research， 2018， 56（24）： 7181-7189. DOI： 10.1080/00207543.2018.1549795.

[11]KIMH J， HARMS R， GNTHER G.et al.Automatic control sequence generation for a hybrid disassembly system[J]. IEEE Transactions on Automation Science and Engineering， 2007， 4（2）： 194-205. DOI： 10.1109/TASE.2006.880538.

[12]MADARN， KALISKY T， COHEN R，et al. Immunization and epidemic dynamics in complex networks[J]. European Physical Journal B， 2004， 38（2）： 269-276. DOI： 10.1140/epjb/e2004-00119-8.

[13]MEYERSL A， POURBOHLOUL B， NEWMAN M E J，et al. Network theory and SARS： predicting outbreak diversity[J]. Journal of Theoretical Biology， 2005， 232（1）： 71-81. DOI： 10.1016/j.jtbi.2004.07.026.

[14]WANGYuhong， CULLINANE K. Measuring container port accessibility： an application of the principal eigenvector method （PEM）[J]. Maritime Economics & Logistics， 2008， 10（1/2）： 75-89.

[15]FREEMANL. Centrality in social networks conceptual clarification[J]. Social Networks， 1979， 1（3）： 215-239. DOI： 10.1016/0378-8733（78）90021-7.

（編辑 赵勉）