半平面问题远域辐射阻尼的时域边界元法模拟研究
2021-04-30李宏军郝文秀龚海天
张 梅, 唐 波,2, 李宏军*, 郝文秀, 龚海天
(1.河北农业大学 城乡建设学院,保定 071001; 2.上海强劲地基工程股份有限公司,上海 200233;3.新加坡清水建设株式会社,新加坡 339509)
1 引 言
当无限及半无限域受到动力荷载作用时,应力波向远域介质传播,能量发生逸散,形成辐射阻尼。辐射阻尼对受力体的动力响应具有重要影响,甚至较之受力体本身阻尼更为重要[1],但半无限域问题中远域辐射条件较难满足,致使远域辐射阻尼的模拟尚没有较为完善的方案。实际工程中诸如岩石基坑爆破开挖、边坡稳定、结构抗震以及结构-地基动力相互作用[2]等问题均会涉及到远域辐射阻尼。
目前处理远域辐射阻尼的方法主要有有限元法与边界元法。由于实际问题应力波的传播距离是有限的,无论采用哪种数值方法,都可以通过截取足够大区域(完全包含应力波的影响范围)进行计算,从而避免辐射阻尼的处理,其操作方法简单,但是离散单元多,计算量较大,对于不同时程需求的问题往往需要多次改变模型,计算繁复。对于有限元法,若截取区域较小(未完全包含应力波的影响范围),需要设置人工边界[3]或直接采用比例边界有限元法[4,5],以考虑远域辐射阻尼的影响。人工边界的引入可以很好地模拟各种无限域的辐射阻尼,但也存在缺点,即低阶边界精度低和高阶边界稳定性较差[6];比例边界元法兼具有限元法和边界元法的优点,是处理远域辐射阻尼的一种较为理想的方法,但由于需要确定固定的比例中心,在求解具有偏心域或平行侧边界的问题时较为困难。对于无限域问题,采用全空间基本解的边界元法,能够自动满足无穷远处的辐射条件,目前国内外对于该问题的研究已经较为成熟[7-10]。对于半无限域问题,国内外学者通过采用基于半空间基本解的边界元法来满足无限长边界上的辐射条件,并进行了较为深入的研究[11-13],然而动力学问题的半空间基本解较为复杂,且边界不规则问题的基本解不易得到,甚至不存在[14,15],使得该方法的通用性不强。在处理半无限域动力学问题时,有较多学者采用基于较为成熟的全空间基本解的时域边界元法[15,16],但由于半无限边界的存在,通常只能截取部分有限边界进行动力分析,不能完全考虑辐射阻尼影响,有些学者在边界离散的基础上采用无穷边界元模拟半无限边界[15,17],对半空间进行频域动力分析,既保证了结果的准确性,又提高了求解效率,但该方法不能求解非线性问题,且需要在频域和时域间多次转换,计算繁复。综上,目前国内外对于半无限域辐射阻尼的模拟尚没有较为完善的方案。
本文以全空间基本解的TD -BEM[7-10]为基础,结合应力波的传播特性,在时域内提出了一种新的单元,即自适应半无限边界单元,专门用于离散远域半无限边界,以考虑远域辐射阻尼,近域边界及无限边界仍采用常规TD -BEM处理。该单元实质上是一个可随时间-空间参数自动调整单元大小的有限单元,因此,可以采用目前已经成熟的数值方法[7,8]对该单元进行处理,理论上不具有困难。
2 半平面问题的时域边界积分方程
在分析半平面问题时,可将其边界划分为有限域边界Γ1、无穷远边界Γ∞及一端延伸到无穷远处的半无限边界Γ2和Γ3,如图1所示。由于Γ∞上的场点都位于无限远处,有限时间段内任意瞬时发出的应力波波前只能到达有限远处,对Γ∞上的场点无任何影响,因此在计算时无需考虑Γ∞。在初始条件为0和忽略体力的条件下,弹性动力学半无限平面问题的时域边界积分方程为
(1)
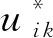
(cs/cd)(Fi k/Ld+Ji kLdNd)Hd]
(2)
(3)
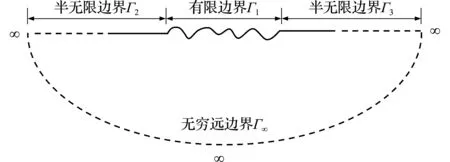
图1 半无限平面边界
式中Ei k=δi k,Fi k=δi k/r2,Ji k=-r,ir,k/r2



Hw=H[cw(t-τ)-r]

3 远域边界的处理方法
有限时间段内的动力学问题,应力波传播距离亦为有限远,对于超过Γ1范围的应力波,应考虑无限域的辐射阻尼,反之,始终处于Γ1范围的应力波不需考虑此效应。实际工程中,涉及无限域的辐射阻尼问题较为常见,为了较好解决这一效应的模拟问题,本文将半无限边界Γ2和Γ3分别采用一个自适应半无限边界单元进行数值离散,半无限边界与有限边界公共点A和应力波的波前位置B分别作为自适应半无限边界单元的内外侧节点,构建自适应半无限边界单元,如图2所示,P点为任意应力波源点,cd(t-τ)为τ时刻作用在源点P处的应力波在t时刻传播的最远距离。根据几何关系,节点B的坐标通式为
(4)
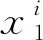
本文提出一种新的单元,即自适应半无限边界单元,专门用于离散远域半无限边界,该单元外侧节点B是一个始终处于应力波波前位置的动态节点,保证计算区域在任何情况下都恰好包含应力波的影响范围,从理论上为远域辐射阻尼的模拟提供保障。
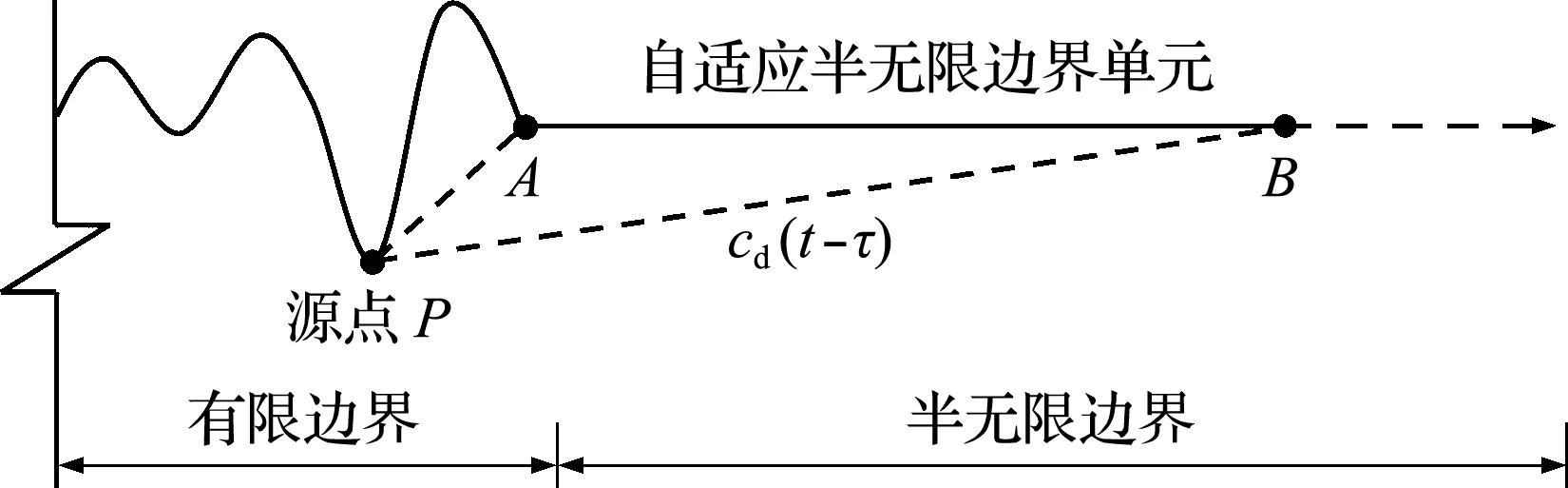
图2 自适应半无限边界单元
4 数值处理
首先将边界进行数值离散,再求出各单元的位移和面力影响系数,最后进行组装形成代数方程组并求解边界点位移。由于边界Γ1为有限边界,其数值处理方法与常规TD -BEM的处理方法完全相同,不再赘述,本节着重介绍半无限边界单元的数值处理。
4.1 数值离散
空间上,根据应力波在弹性介质中的传播特性,将两侧的半无限边界转化为两个自适应半无限边界单元。假定面力和位移在半无限边界单元上线性变化,其插值函数表达式为
(5)
式中ξ为自然坐标,取值范围为[-1,1]。
时间上,将时间域[0,t]离散为M个步长为Δt=t/M的时间单元。且令时间节点tm=mΔt,其中m取值范围为0,1,…,M。假定在每一时间步上面力为常量,位移线性变化,对于任意时间单元,面力和位移的插值函数分别为
(6,7)
离散后,单元面力影响系数gi k与位移影响系数hi k表达式为
(8)
式中a,b=1或2。
4.2 影响系数的求解
通过数值离散,将边界积分方程的半无限边界部分转化为自适应半无限边界单元积分,积分中奇异性情况及求解方法如下。
(1) 无奇异性。采用高斯数值积分法计算。
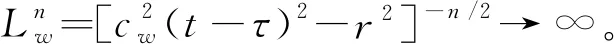
(9)
(10)
式中 表示Hadamard主值积分的计算符号。
(3) 空间奇异性。此时r→0,奇异性的表现形式为1/rn→∞。这类奇异性可通过考虑P波及S波的相互作用,将两种波对应的数学表达式进行代数求和,采用分子有理化的数学方法对奇异积分解析求解,可表示为
(11)
(4) 双重奇异性。即同时具有波前和空间奇异性。这类奇异性需要在波前及空间奇异性处理的基础上,再通过在空间上影响系数组装时,考虑变形协调条件联系奇异点两侧单元影响,将两侧单元相应表达式进行代数求和,即可解析互消。
按以上方法求解,可以得到各单元的影响系数。
4.3 组装
(12)
(e=2~Ne-1)(13)
5 验 证
5.1 算例描述
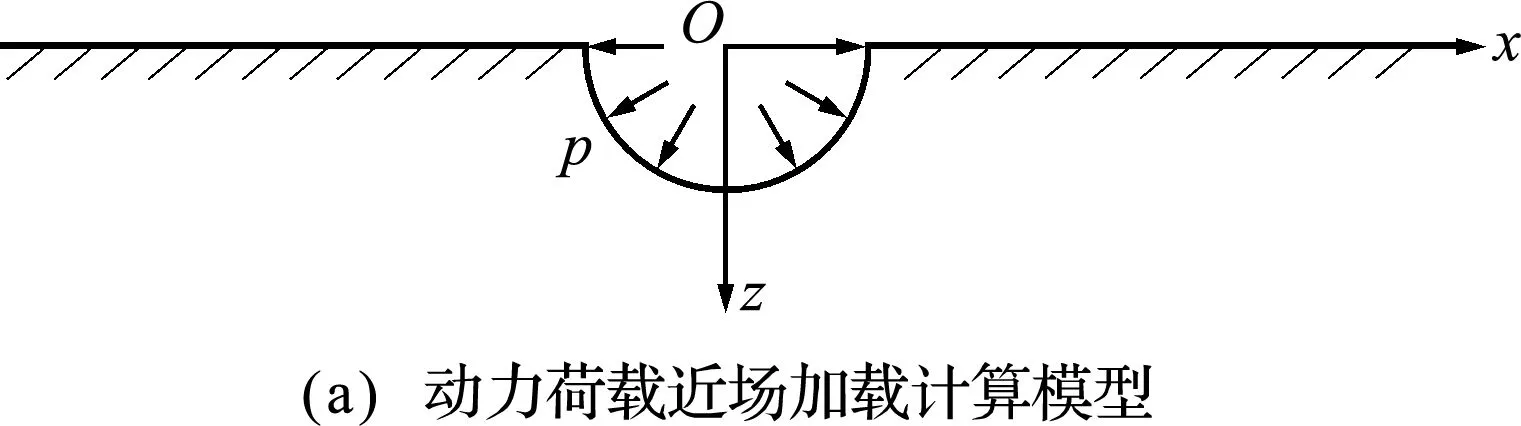
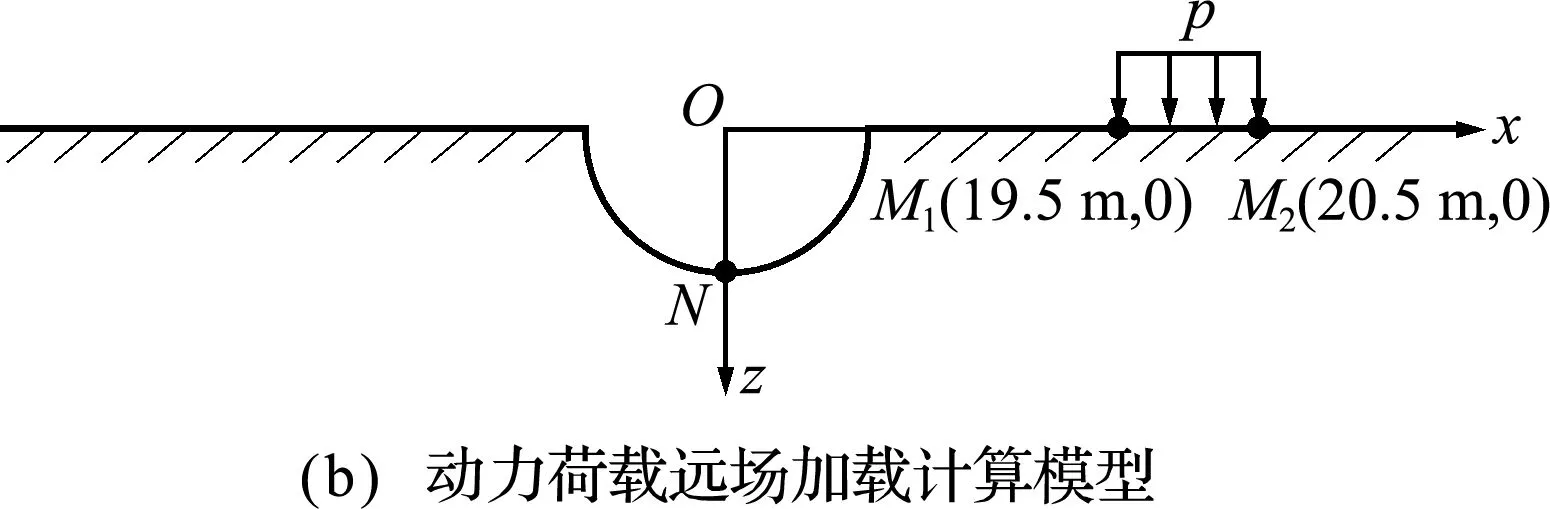
图3 动力荷载作用下的弹性半平面计算模型
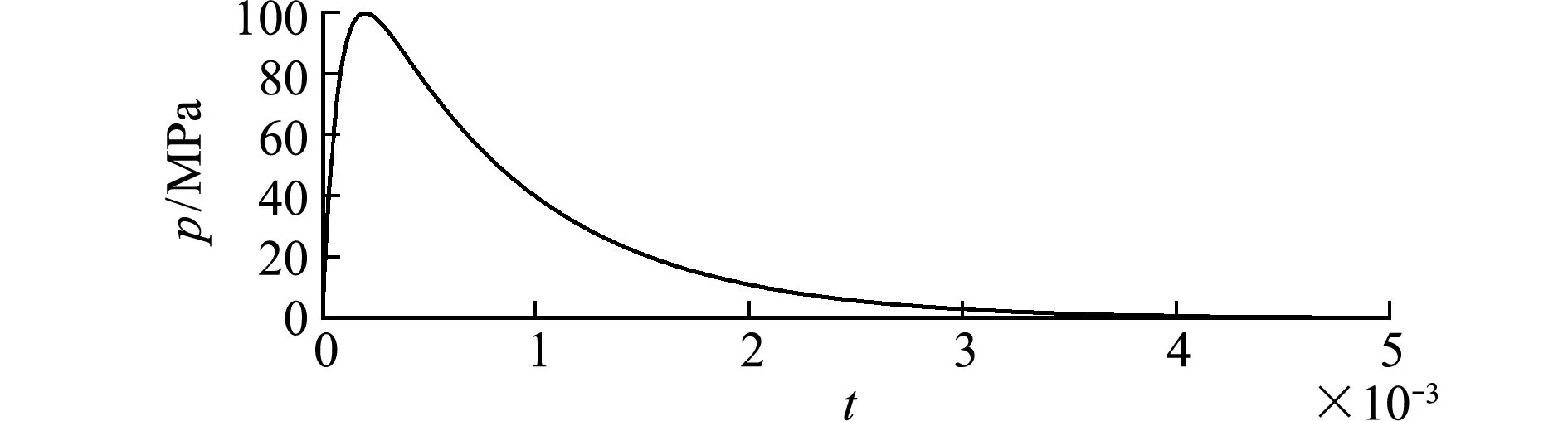
图4 动力荷载函数图像
5.2 对比验证方案
采用3种方案对两种加载方式的算例进行求解,并将计算结果进行对比验证。
(1) 采用FEM(ANSYS)计算,取距荷载60 m范围内的区域作为计算域,共离散了44984个PLANE42单元。
(2) 采用常规TD -BEM求解,取距原点25 m以内区域进行计算,共离散500个有限边界单元。
(3) 采用结合自适应半无限边界单元的时域边界元法求解(下称自适应TD -BEM),与方案(2)相比,仅在有限边界两侧各添加了一个自适应半无限边界单元,其他处理保持不变。
此处需要说明,离散系数β[9](β=cdΔt/lmax,lmax为最大单元长度)是影响TD -BEM计算精度的重要因素之一。对比半平面问题β=0.5~3.0 时的计算结果,发现β=1.5~2.5时,较为理想。因此,方案(2,3)选取了β=2对有限域边界进行离散。
5.3 计算结果及讨论
近场加载选取地表r=10 m和20 m处节点的位移响应进行比对,结果如图5和图6所示;远场加载选取沟槽底部N点进行比对,结果如图7所示(注:图5~图7设置为每6个时间步显示一个结果点,并对横坐标时间变量进行了无量纲化处理)。
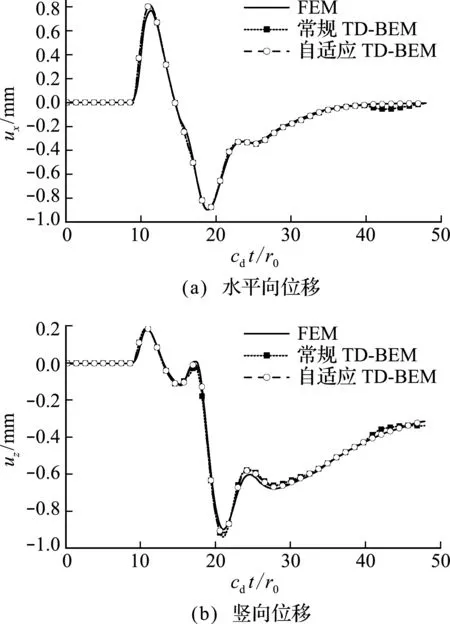
图5 近场加载r =10 m处计算结果
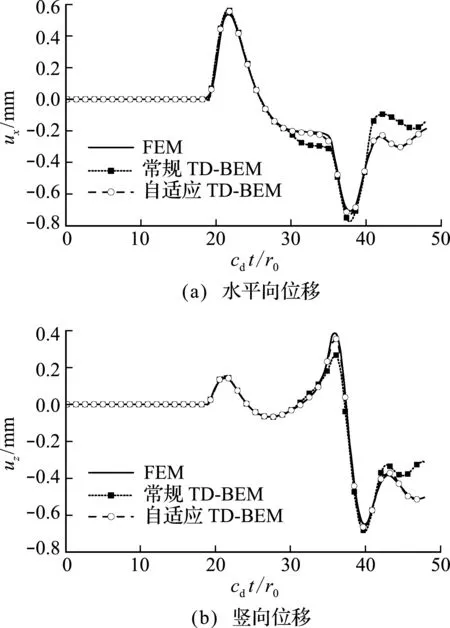
图6 近场加载r =20 m处计算结果
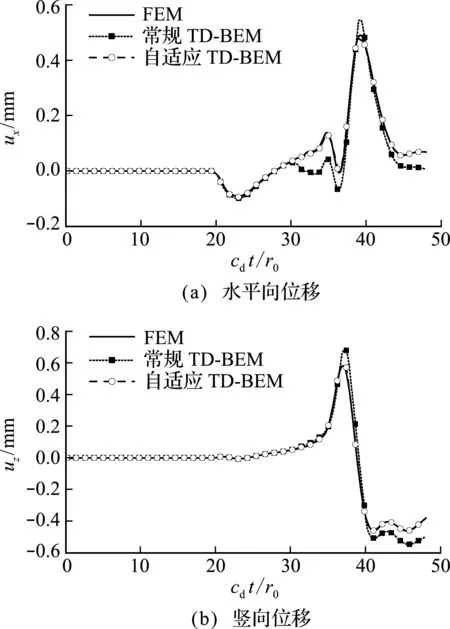
图7 远场加载节点N计算结果
计算结果表明,常规TD -BEM由于仅截取了部分有限边界进行计算,不能考虑应力波在远域的辐射条件,应力波出现了回弹,近场入射r=10 m和20 m地表处以及远场入射的节点N处,分别在cdt/r0=40,30和30时,回弹应力波刚好到达计算点,节点在受到回弹应力波的影响后,其位移与FEM结果相比出现较大差异;而自适应TD -BEM得到的结果能够与FEM结果吻合良好,满足了应力波在半无限域上的辐射条件,较好地模拟了远域辐射阻尼效应。
如果想要通过常规TD -BEM得到更精确的结果,势必要扩大计算范围,离散更多的网格。而自适应TD -BEM仅在原有限边界的基础上添加两个自适应半无限边界单元,即可自动满足半无限域的辐射条件,在计算时间成本与常规TD -BEM几乎相同的情况下,得到了较高精度的计算结果。
6 结 论
本文根据应力波在弹性介质中的传播特性,将半无限边界转化为自适应半无限边界单元,该单元可根据具体的时间-空间参数自动调节单元大小,保证计算区域在任何情况下都恰好包含应力波的影响范围,满足了应力波在半无限域上的辐射条件。采用自适应半无限边界单元的TD -BEM较好地解决了远域辐射阻尼的模拟问题,且在计算时间成本与常规TD -BEM几乎相同的前提下,具有更高的计算精度。
需要说明的是,本文以弹性动力学问题为切入点,重点研究远域辐射阻尼的模拟方法。对于非线性动力学问题,足够远域介质往往处于弹性阶段,因此,本文提出的基于TD -BEM的自适应半无限边界单元模拟远域辐射阻尼的方法和结论依然是适用的。对于近域非线性问题TD -BEM的详细介绍可参见文献[20,21]。
