单纤维捕集过程中亚微米颗粒的布朗团聚

张俪安,刁永发,楚明浩,王如歌,沈恒根

单纤维捕集过程中亚微米颗粒的布朗团聚

张俪安,刁永发*,楚明浩,王如歌,沈恒根

(东华大学环境科学与工程学院,上海 201620)

针对亚微米颗粒(0.1~0.5μm)在单纤维捕集过程中的布朗团聚规律,基于计算流体动力学-颗粒群平衡模型(CFD-PBM)对粉尘颗粒在单纤维捕集过程中的布朗团聚行为进行了数值模拟研究,采用分区法对颗粒群平衡方程(PBE)进行求解,综合考虑了停留时间、入口粉尘粒径、气流温度、数对布朗团聚的影响,并将数值模拟与实验结果进行对比.结果表明,布朗团聚核UDF符合数值模拟计算要求.粉尘颗粒的布朗团聚贯穿整个过程,团聚有效时间=/(速度方向模型尺寸长度/入口流速);粉尘颗粒越小,布朗团聚越强,Bin-7与Bin-0区间的数量浓度差距越小,粒径与布朗团聚强度呈负相关;气流温度是通过改变气流动力黏度以及聚并系数来影响布朗团聚,与布朗团聚强度呈正相关,当=300K,p³0.5μm时,颗粒的布朗团聚效应可以忽略;数通过扩散系数的变化影响布朗团聚,与布朗团聚强度呈负相关.

亚微米颗粒；CFD-PBM；布朗团聚；分区法；单纤维

PM2.5等微细颗粒物对人体免疫系统、呼吸系统和中枢神经系统都有着不良影响[1].目前工业上袋式除尘器对于PM2.5以下的颗粒存在穿透区,纤维难以捕集[2].

目前国内外对于纤维捕集颗粒物的研究主要包括纤维截面形状(异型纤维)[3-4]、纤维直径[5]、填充率[6]、颗粒物沉积特性[7-9]以及纤维排列结构[1,10]和纤维交叉角度[11]等参数的变化对捕集效率和压降的影响.所研究的粒径区间主要集中在两个范围,一方面p>0.5μm粒径段范围,该区间粒径较大,布朗运动效应基本可以忽略,其纤维捕集颗粒时主要依靠惯性碰撞和拦截效应.另一方面p£0.5μm粒径段时存在一部分亚微米级颗粒(0.1~0.5μm)[12],在流场中会由于布朗效应做无规则运动,此时布朗运动已经不能忽略,纤维捕集颗粒主要依靠粉尘颗粒的布朗效应,且颗粒由于布朗扩散作用被纤维捕集的效率计算公式繁多[13-16].基于计算流体动力学-离散相模型(CFD-DPM),添加布朗力UDF或Boltzmann法模拟可以计算出粉尘颗粒因布朗运动而被纤维捕集的运动轨迹或过滤性能,进而得出颗粒做布朗运动的相关信息[17-18].但是,布朗团聚信息仅仅依靠CFD-DPM等方法并不能很好的得出计算结果,该方法在计算时忽略了颗粒与颗粒之间的相互作用[19].

为了更好地探究出单纤维捕集过程中亚微米级颗粒因布朗运动而团聚的现象,基于CFD-PBM,采用分区法对颗粒群平衡方程进行求解,进而对整个过程进行数值模拟,而对于分区法则是把颗粒尺寸分布曲线进行离散,划分为有限数目的个区间,认为每个区间内颗粒尺度分布满足一个统一的分布函数,在每个区间内针对某个颗粒属性的分布函数,建立平衡方程,联立求解平衡方程,可以得到某个颗粒属性的分布函数随时间演变的过程.

同时,模拟的颗粒尺寸范围选择0.1~0.5μm粒径段.根据文献[20]研究结果,当0.1μm£p£0.4μm,随着粒径的减小,布朗团聚开始逐渐增强.在研究亚微米颗粒布朗团聚过程中,通过编写UDF在PBM模型中添加布朗团聚核函数,以实现颗粒在流场中的布朗团聚过程,改变停留时间、入口粉尘粒径、气流温度、数等工况来探究对流场中亚微米颗粒布朗团聚的影响.为后续开展纤维捕集亚微米颗粒的数值模拟提供借鉴.

1 数值计算模型

1.1 多相流模型

多相流模型采用欧拉-欧拉双流体模型,连续性方程和动量方程如下[7]:

式中:为流体的密度,kg/m3;为体积分数项;是流体的速度,m/s;为计算单元的压力,N;为流体黏附性应力张量;为重力加速度,m/s2;为网格单元内受到的综合作用力,N.

1.2 颗粒群平衡方程

颗粒的团聚可以用粒子聚并的动力学方程(GDE/PBE)来进行描述,聚并动力学方程如下[21]:

1.3 布朗团聚核

Knudesn数可用来表征颗粒和环境气体之间的质量、动量和能量的交换和转移,且根据颗粒的数将颗粒分为自由分子区、过渡区、近连续区(或滑流区)和连续区,其表达式如下[22]:

式中:为空气分子的平均自由程,nm;为颗粒的半径,μm;p为颗粒直径,μm.

根据Allen等[23]空气的平均自由程的计算式如下:

表1 不同直径颗粒的Kn值大小(300K)

通过大小和表2的范围可知,0.2~0.5μm范围内的颗粒属于近连续区/滑流区(0.1££1),当p=0.1μm时,=1.368,但由于0.1μm的颗粒仍接近于近连续区间,为了简化研究,考虑同样属于近连续区间.

对于近连续区/滑流区的布朗团聚核为[22]:

式中:d和d分别为颗粒的直径,μm;co为连续区及近似连续区的碰撞系数;B为玻尔兹曼常数, 1.380649×10-23J/K;为气流的动力黏度,Pa·s;0= 1.83245×10-5Pa·s;为气流的绝对温度,K;0和S为温度常数,K;为环境气体的绝对温度,K.

表2 不同直径颗粒的Kn数和区域(温度300~2000K)[22]

对于连续区,Stokes-Cunningham,滑移修正系数c=1,对于近似连续区,一般c的计算式如下[24]:

2 边界条件

对颗粒群平衡方程PBE采用分区算法,初始颗粒分布为单分散相体系,以入口颗粒粒径为0.2μm为例,将颗粒群大小划分为8个子区间, Bin-7~Bin-0区间粒径大小由初始通入颗粒的粒径计算得来,(分区后,相邻区间后一区间颗粒体积与前一区间颗粒体积满足k+1=sk, 1.08£s£3.0),Ratio Exponent数值取1.0满足要求,在每个子区间内对群体平衡模型进行积分即可得到一系列离散的方程,表3为初始计算时各区间对应的粒径大小和体积分数.

图1 计算区域及边界条件示意

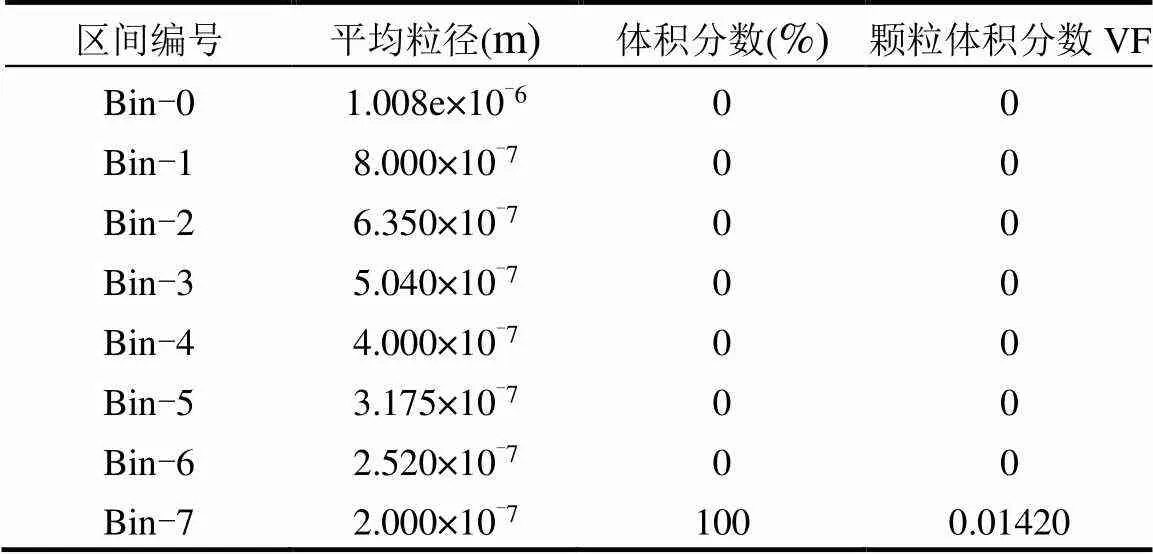
表3 Bin-7-Bin-0区间粒径大小以及初始体积分数

注:不同的入口粒径对应不同组的Bin-7~Bin-0.

3 模型正确性验证

对于模型的正确性验证包括网格独立性检验以及布朗团聚核UDF检验,单纤维捕集结构模型根据[26]计算结果选取50多万六面体结构化网格进行数值模拟计算,对比进出口压降,与Darcy压降经验公式(8)误差在5%范围内.

而对于布朗团聚核的正确性根据徐俊波等[27]的实验数据进行验证,以0.5μm聚并乙烯标准微球通入凝并器为例,物理和化学特性比较稳定,密度为783kg/m3,颗粒入口的固含率为10-6,入口气流速度为3.5L/min,通过计算<2300,流动为层流,颗粒间不存在湍流团聚.空气为连续相,并采用不可压缩流体描述,密度为1.225kg/m3,气固两相流的曳力系数根据Schiller-naumann关联式,由于p=0.5μm,= 0.2736,处于近连续区/滑流区,符合布朗团聚核UDF的验证,数值模拟结果如图2所示:

由图2可知,凝并器出口颗粒分布呈多分散相分布,粒径尺寸趋向于大颗粒偏移,且分布主要集中在0.5~1.0μm之间,模拟结果与实验结果定性一致,而在实验结果中出现的低于0.5μm的颗粒原因可能是实验过程中凝并器被环境气体污染及实验过程污染等因素,数值模拟结果0.5μm颗粒较多是由于团聚时间短,大量的初始颗粒还未团聚.

图2 数值模拟与实验结果对比

式中:D为进出口压降,Pa;为填充率;为流体的动力黏度,Pa·s;颗粒入口风速,m/s;为过滤层厚度,µm;f为纤维直径,μm.

4 数值模拟计算

4.1 停留时间对布朗团聚影响

如图3(a)所示,单纤维捕集过程中存在明显的布朗团聚行为,粉尘颗粒的布朗团聚贯穿整个过程,随着停留时间的增加,Bin-7区间颗粒数量浓度逐渐减小,粉尘颗粒逐渐向大颗粒偏移,布朗团聚的效果越来越明显,当=/时(速度方向模型尺寸长度/入口流速),颗粒数量浓度基本不变,颗粒流出单纤维捕集结构,布朗团聚过程结束.

通过多项式拟合,由图3(b)出口平均粒径与停留时间变化曲线可知,随着停留时间的增加,出口平均粒径随着停留时间是逐渐增加的,且逐渐趋于稳定,出口颗粒平均粒径与停留时间满足一元二次多项式关系,表达式如下:

Ave=+-2(、、均为常数)(9)

4.2 入口粉尘粒径对布朗团聚影响

如图4(a)可知,入口粒径越小,Bin-7与Bin-0区间颗粒数量浓度差距越小,粉尘颗粒的布朗团聚效果越强.这是因为粉尘颗粒粒径越小,布朗运动强度越强,碰撞几率越大;同时,粉尘颗粒体积分数一定时,粒径越小,则单纤维捕集结构中所含有的颗粒数越多,同样增加了粉尘颗粒的碰撞几率,对于颗粒的团聚有促进作用,粒径的大小与布朗团聚强度呈负相关.

对于曲线中凸点的出现是因为亚微米颗粒在流场中发生布朗团聚后,颗粒变化过程是(Bin-7→Bin-6→Bin-5→Bin-4→Bin-3→Bin-2→Bin-1→Bin-0),Bin-7区间的颗粒数量浓度会减小,逐渐由小颗粒向大颗粒变化,Bin-6~Bin-0区间的颗粒数量浓度会增加,若布朗团聚效果明显,有效团聚时间内, Bin-7区间颗粒数量浓度下降多,此时凸点就会产生,若布朗团聚效果不明显,Bin-7区间颗粒数量浓度下降少,Bin-6~Bin-0区间颗粒数量浓度小于Bin-7时就不会产生凸点.

Ave=A-Bp+Cp2-Dp3+Ep4

(A、B、C、D均为常数)(10)

4.3 气流温度对布朗团聚影响

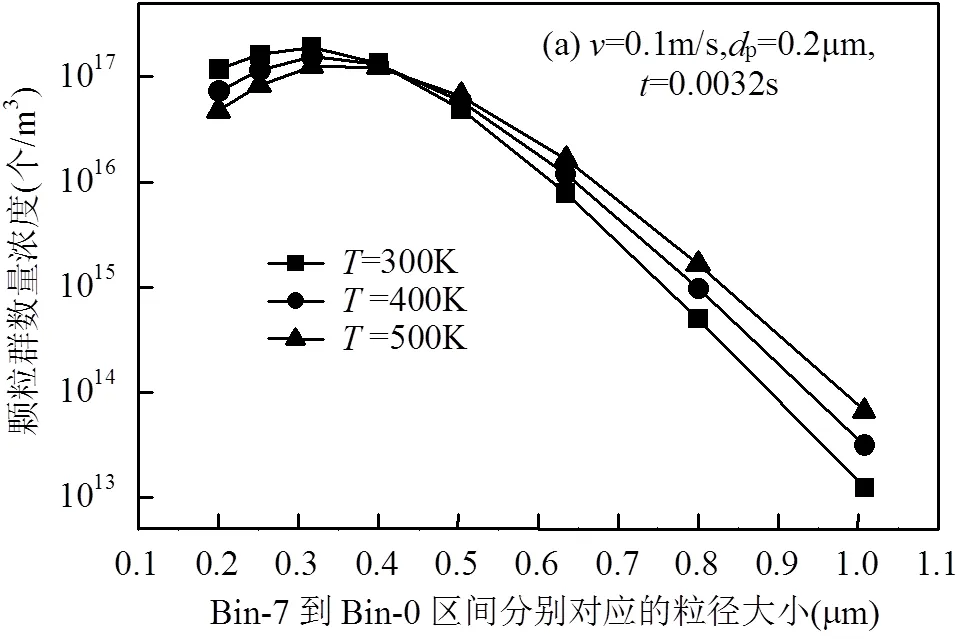
如图5(a)所示,图中3条曲线分别为流体温度为300,400和500K时的数值模拟结果.由图可知,粉尘颗粒的布朗团聚效果随着气流温度的提高而增大,这是因为气流温度改变导致气流的动力黏度以及聚并系数发生改变,当温度由300K增加到500K时,聚并系数co由1.492´10-16增加到1.719´10-16,聚并系数的增加直接导致团聚的增强.同时温度升高,颗粒的布朗运动越剧烈,促进了粉尘颗粒的团聚,气流温度对于粉尘颗粒的布朗团聚效果呈正相关.

通过多项式拟合,由图5(b)出口平均粒径与气流温度变化曲线可知,随着气流温度的增加,出口处平均粒径随着气流温度变化逐渐增加,出口处平均粒径与气流温度满足一次函数关系式,表达式如下:

Ave=A+B(A、B均为常数)(11)

4.4 Pe数对布朗团聚影响

数对于布朗扩散的影响主要来源于与粉尘颗粒的扩散系数有直接的关系,由公式(12)可知,数与扩散系数成反比关系,数越小,此时粉尘颗粒的扩散系数越大,粉尘颗粒的运动越剧烈,加剧了布朗扩散运动,因此团聚强度增强,计算公式如下:

对于颗粒的扩散,又称布朗扩散,扩散系数由斯托克斯-爱因斯坦提出[28]:

式中:B为玻尔兹曼常数,B=1.380649´10-23J/K;为环境气体的绝对温度,K;为动力黏度,Pa·s;C为库宁汉滑移修正系数;为粒子的迁移速率,m2/(N·s).

如图6(a)所示, 图中3条曲线分别为数为88.03、66.42和51.81时的数值模拟结果.粉尘颗粒的布朗团聚效果随着数的减小而增大,这是因为数由88.03减小到51.81时,扩散系数由2.272× 10-10m2/s增加到3.860×10-10m2/s,扩散系数的增加直接导致布朗团聚的增强.

通过多项式拟合,由图6(b)出口平均粒径与变化曲线可知,随着数的增加,出口处平均粒径随着逐渐减小的,出口处平均粒径与数满足一元二次多项式关系,表达式如下:

Ave=-2(、、均为常数)(14)

5 结论

5.1 对于亚微米级颗粒来说,单纤维捕集结构中存在明显的布朗团聚行为,且贯穿整个捕集过程,团聚有效时间=/,出口平均粒径与停留时间呈一元二次多项式关系.

5.2 粉尘颗粒越小,布朗运动的强度越大,布朗团聚效果越强,出口处平均粒径与入口粒径相比增加的倍率越大,当=300K,p³0.5μm时,颗粒的布朗团聚效应可以忽略,粒径的大小与布朗团聚强度呈负相关.

5.3 粉尘颗粒的布朗团聚效果随着温度的提高而增大,气流温度越大,颗粒的布朗运动越剧烈,粉尘颗粒的布朗团聚效果越强,对于粉尘颗粒的布朗团聚强度呈正相关,出口平均粒径与气流温度呈一次函数关系;

5.4数与扩散系数成反比关系,数越小,粉尘颗粒的运动越剧烈,粉尘颗粒的布朗团聚效果越强,数与布朗团聚强度呈负相关,出口平均粒径与数呈一元二次关系式.

[1] Li W, Shen S N, Li H. Study and optimization of the filtration performance of multi-fiber filter [J]. Advanced Powder Technology, 2016,27:638-645.

[2] 熊桂龙,李水清,陈 晟,等.增强PM2.5脱除的新型电除尘技术的发展[J]. 中国电机工程学报, 2015,35(9):2217-2223. Xiong G L, Li S Q, Chen S, et al. Development of advanced electrostatic precipitation technologies for reducing PM2.5emissions from coal-fired power plants [J]. Proceedings of the CSEE, 2015, 35(9):2217-2223.

[3] Hosseini S A, Tafreshi H V. On the importance of fibers' cross- sectional shape for air filters operating in the slip flow regime [J]. Powder Technology, 2011,212(3):425-431.

[4] 朱 辉,杨 会,付海明,等.椭圆纤维过滤压降与惯性捕集效率数值分析[J]. 中国环境科学, 2019,39(2):119-127. Zhu H, Yang H, Fu H M, et al. Numerical analysis of filtration pressure drop and inertial collection efficiency for elliptical fibers [J]. China Environmental Science, 2019,39(2):119-127.

[5] Bucher T M, Vahedi Tafreshi H, Tepper G C. Modeling performance of thin fibrous coatings with orthogonally layered nanofibers for improved aerosol filtration [J]. Powder Technology, 2013,249:43-53.

[6] Hosseini S A, Tafreshi H V. 3-D simulation of particle filtration in electrospun nanofibrous filters [J]. Powder Technology, 2010,201(2): 153-160.

[7] Qian F P, Huang N J, Zhu X J, et al. Numerical study of the gas-solid flow characteristic of fibrous media based on SEM using CFD-DEM [J]. Powder Technology, 2013,249:63-70.

[8] Yue C, Zhang Q, Zhai Z Q. Numerical simulation of the filtration process in fibrous filters using CFD-DEM method [J]. Journal of Aerosol Science, 2016,101:174-187.

[9] Kasper G, Schollmeier S, Meyer J. Structure and density of deposits formed on filter fibers by inertial particle deposition and bounce [J]. Journal of Aerosol Science, 2010,41(12):1167-1182.

[10] Wang H M, Zhao H B, Wang K, et al. Simulation of filtration process for multi-fiber filter using the Lattice-Boltzmann two-phase flow model [J]. Journal of Aerosol Science, 2013,66:164-178.

[11] Fotovati S, Tafreshi H V, Pourdeyhimi B. Influence of fiber orientation distribution on performance of aerosol filtration media [J]. Chemical Engineering Science, 2010,65(18):5285-5293.

[12] 周 科,徐明厚,于墩喜,等.混煤燃烧减小细微颗粒物生成的实验研究[J]. 工程热物理学报, 2011,32(2):349-352. Zhou K, Xu M H, Yu D X, et al. Experimental study of coal blend combustion for fine particulates reduction [J]. Journal of Engineering Reduction Thermophysics, 2011,32(2):349-352.

[13] Fuchs N A, Stechkina I B. A note on the theory of fibrous aerosol filters [J]. Annals of Occupational Hygiene, 1963,6(1):27-30.

[14] Stechkina I B, Fuchs N A. Studies on fibrous aerosol filters-I. Calculation of diffusional deposition of aerosols in fibrous filters [J]. Annals of Occupational Hygiene, 1966,9(2):59-64.

[15] Lee K W, Liu B Y H. Theoretical study of aerosol filtration by fibrous filters [J]. Aerosol Science and Technology, 1982,1(2):147-161.

[16] Payet S, Boulaud D, Madelaine G, et al. Penetration and pressure drop of a HEPA filter during loading with submicron liquid particles [J]. Journal of Aerosol Science, 1992,23(7):723-735.

[17] Wang H M, Zhao H B, Guo Z L, et al. Numerical simulation of particle capture process of fibrous filters using Lattice Boltzmann two-phase flow model [J]. Powder Technology, 2012,227:117-122.

[18] Kang S K, Lee H, Kim S C, et al. Modeling of fibrous filter media for ultrafine particle filtration [J]. Separation & Purification Technology, 2019,209:461-469.

[19] 黄乃金,钱付平,查文娟,等.基于微观结构的褶式滤芯拟态化模拟及其过滤性能的数值模拟[J]. 过程工程学报, 2014,14(3):402-408. Huang N J, Qian F P, Zha W J, et al. Modeling of the pleated filter based on microscopic structure and numerical simulation of its filtration characteristics [J]. The Chinese Journal of Process Engineering, 2014,14(3):402-408.

[20] 甘 莉,柳朝晖,李瑞霞,等.均匀湍流内湍流-布朗颗粒碰撞的直接数值模拟研究 [C]. 重庆:中国工程热物理学会多相流学术会议, 2006:581-585. Gan L, Liu Z H, Li R X, et al. Direct numerical simulation of turbulent-Brown particle collision in uniform turbulence, Chongqing: Chinese Society of Engineering Thermophysics Multiphase Flow Conference. 2006:581-585.

[21] Piskunov V N, Golubev A I, Barrett J C, et al. The generalized approximation method for modeling coagulation kinetics-part 2: comparison with other methods [J]. Journal of Aerosol Science, 2002,33(1):65-75.

[22] 赵海波,郑楚光.离散系统动力学演变过程的颗粒群平衡模拟[M]. 北京:科学出版社, 2008:28. Zhao H B, Zheng C G. Particle swarm equilibrium simulation of the evolution process of discrete system dynamics [M]. Beijing: Science Press, 2008,2008:28.

[23] Allen M D, Raabe O G. Slip correction measurements of spherical solid aerosol particles in an improved millikan apparatus [J]. Aerosol Science and Technology, 1985,4(3):269-286.

[24] Randerson D. Atmospheric science and power production [C]. Washington D C: Division of Biomedical Environmental Research, US department of Energy, 1983.

[25] Davies C N, The separation of airborne dust and particles [J]. Proceedings of the Institution of Mechanical Engineers, 1952,1(5): 393-427.

[26] 张俪安,刁永发,庄加玮,等.高梯度磁场提升单纤维捕集PM2.5性能的机理[J]. 中国环境科学, 2019,39(7):2765-2773. Zhang L A, Diao Y F, Zhuang J W. The mechanism of high gradient magnetic field improving the performance of single fiber capture PM2.5[J]. China Environmental Science, 2019,39(7):2765-2773.

[27] 徐俊波,张 丽,岳仁亮,等.PM2.5细颗粒物凝并的计算流体力学模拟 [J]. 计算机与应用化学, 2013,30(8):3-6. Xu J B, Zhang L, Yue R L, et al. CFD simulation on the aggregation of PM2.5fine particles [J]. Computers and Applied Chemistry, 2013,30(8): 3-6.

[28] 向晓东.气溶胶科学技术与基础 [M]. 北京:中国环境出版社, 2012: 71. Xiang X D. Aerosol science technology and foundation [M]. Beijing: China Environment Press, 2012:71.

Brownian aggregation in the process of submicron particles captured by single fiber.

ZHANG Li-an, DIAO Yong-fa*, CHU Ming-hao, WANG Ru-ge, SHEN Heng-gen

(College of Environmental Science and Engineering, Donghua University, Shanghai 201620, China)., 2021,41(4)：1548~1554

In view of the Brownian aggregation law in the process of submicron particles (0.1~0.5μm) captured by single fiber, the Brownian aggregation behavior in the process of the dust particles captured by single fiber was numerically studied based on computational fluid dynamics-population balance model (CFD-PBM), and the partition method was used to solve population balance equation (PBE). The effects of residence time, inlet particle diameter, airflow temperature, andnumber on the Brownian aggregation were considered comprehensively, and the numerical simulation and experimental results were compared. The results showed that the Brownian aggregation kernel met the requirements of numerical simulation calculation. The Brownian aggregation of dust particles run through the entire process, aggregation effective time=/(dimension length along with flow field direction/face velocity). The smaller the dust particles, the stronger the intensity of the Brownian motion, the smaller the number density gap between Bin-7 and Bin-0, and the particle diameter was negatively correlated with the Brownian aggregation intensity. Brownian aggregation was affected by airflow temperature by changing flow field dynamic viscosity and aggregation coefficient, which was positively correlated with the Brownian aggregation intensity, when=300K,p³0.5μm, the Brownian aggregation effect of particles can be ignored; Brownian aggregation was influenced by the change ofnumber through the change of diffusion coefficient, which was negatively correlated with the Brownian aggregation intensity.

submicron particles；CFD-PBM；Brownian aggregation；partition method；single fiber

X513

A

1000-6923(2021)04-1548-07

张俪安(1990-),男,安徽省淮北市人,东华大学博士研究生,主要从事粉尘磁团聚研究.发表论文4篇.

2020-08-16

国家重点研发计划项目(2018YFC0705300);中央高校基本科研业务费重点项目(2232017A-09);中央高校基本科研业务费专项资金、东华大学研究生创新基金资助项目(CUSF-DH-D-2020067)

* 责任作者, 教授, diaoyongfa@dhu.edu.cn