流变对狭窄河谷高面板堆石坝应力变形的影响
2021-04-30袁丽娜向国兴
欧 波 袁丽娜 向国兴
(贵州省水利水电勘测设计研究院有限公司,贵州 贵阳 550002)
1 引 言
进入21世纪以来,混凝土面板堆石坝因其自身优点在国内外得到广泛应用,并且面板坝的坝高也在逐渐增加。然而,修建于狭窄河谷中的高面板坝数量相对较少,尤其是200m级的高面板堆石坝,比较有名的包括国外澳大利亚的Cethana坝,坝高110m,河谷宽高比1.94;委内瑞拉的Yacambu坝,坝高162m,河谷宽高比0.9;中国的吉林台面板坝,坝高157m,河谷宽高比2.48;洪家渡面板坝,坝高179.5m,河谷宽高比2.49等。在狭窄河谷地形约束下,高面板堆石坝的变形呈现出不同于宽缓河谷的特性,对于200m级高面板堆石坝,大坝堆石体流变变形的存在使得堆石体后期变形量较大,对坝体和面板应力变形等都有一定影响。因此,对狭窄河谷高面板堆石坝设计时应特别考虑时间效应,以便客观合理地计算堆石体流变变形的影响,并采取相应的工程措施减少堆石体流变对坝体应力和面板变形的影响。
黔中平寨水库混凝土面板堆石坝是建于贵州省喀斯特狭窄河谷地区的高面板堆石坝,基于已建类似工程的经验,采用大坝堆石料的流变模型和三维有限元数值模拟,分析流变特性对面板堆石坝竣工期、蓄水期以及运行期应力变形特性的影响。
2 平寨水库面板堆石坝的概况
平寨水库混凝土面板堆石坝位于贵州省三岔河中游,坝址以上集水面积3492km2,水库总库容10.89亿m3,最大坝高157.5m,坝顶高程1335m,坝顶长355m,坝顶宽10.3m。大坝上游坝坡(面板顶部)1∶1.404,下游坝面设置宽度8m的“之”字形公路,综合坝坡1∶1.533。坝址位于平寨峡谷河段,河谷宽高比为2.2,两岸左缓右陡呈现不对称的“V”形谷,见图1。
坝体从上游至下游依次分为石渣料盖重区(1B)、黏土铺盖区(1A)、防渗区(混凝土面板及止水设施F)、垫层料区(2A)、过渡料区(3A)、上游堆石区(3B)、下游堆石区(3C)、下游堆石排水区(3F)等8个区,见图2。其中面板分两期浇筑,大坝填筑至1255m高程后,浇筑Ⅰ期面板至1244m高程;大坝填筑至坝顶后,浇筑Ⅱ期面板至坝顶,大坝土石方开挖量约为50万m3,坝体填筑量约为520万m3。

图1 平寨面板坝坝轴线剖面图
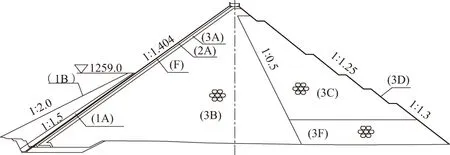
图2 平寨面板坝坝体典型剖面图
3 堆石料的流变模型
目前描述流变特性的主要方法有两种:ⓐ试验结果拟合的经验曲线;ⓑ流变模型。黔中平寨水库混凝土面板堆石坝采用南京水利科学研究院的大型数控流变仪对主堆石料和次堆石料等进行三轴流变试验。其中,主堆石料围压为1000kPa,应力水平分别为0、0.4、0.8三种状态下的实验结果见图3。
流变试验参数的整理采用三参数模型进行,由于该模型简单实用,因此被广泛应用于数值分析中。流变计算模型选用以指数型衰减的Merchant模型来模拟常应力下的ε-t衰减曲线,其蠕变曲线可以写为
εt=εi+εf(1-e-αt)
(1)
式中,εi为瞬时变形,kPa,可假定由弹塑性模型求得的变形为此瞬时变形;εf为随时间发展的最终变形量,kPa;εt为t时刻的流量变形量,kPa。
式(1)求导,可得
(2)
由式(2)可见,αεf为t=0时的初始变形率,α为初始相对变形率(即第一天的流变量占总流变量之比),
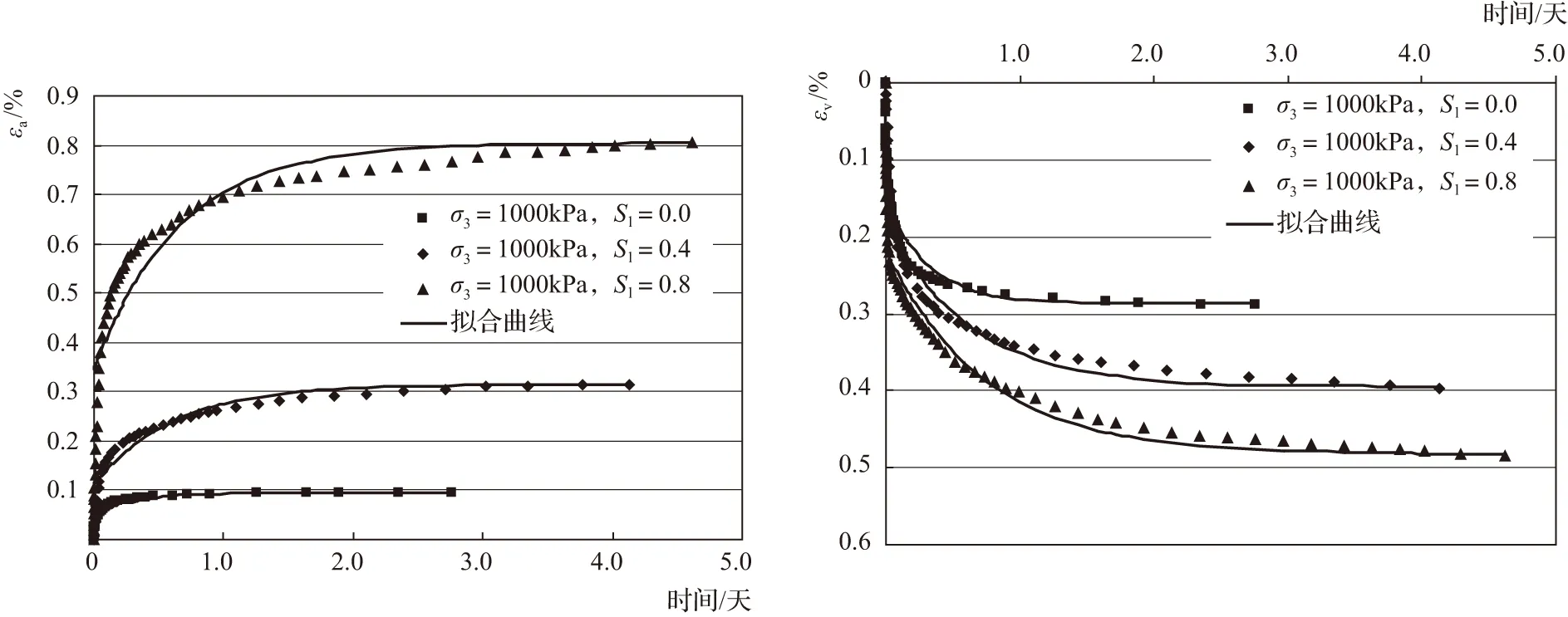
图3 主堆石区流变试验曲线
e为自然常数。故上式可以写为
(3)
在Prandtl-Reuss的假设下,应变率的张量可以表示为
(4)
式中,{s}为偏应力,kPa;σs为广义剪应力,kPa。
针对筑坝材料分别对体积变形和剪切变形假定了下列变形速率,可表示为
(5)
(6)
式中,εVf和γf分别为最终体积流变和最终剪切流变,kPa;可用下列公式表示
(7)
(8)
式中,σ3为围压,kPa;b、d为计算参数,b相当于σ3=Pa(大气压,100kPa)时的最终体积流变量,d为应力水平Sl为0.5时的最终剪切流变量;破坏时Sl为1,γf→∞。而εVt和γt为t时段已积累的体积变形和剪切变形,kPa;由下式计算
(9)
(10)
式(9)和式(10)中采用了相对时间而不用绝对时间的策略,克服了由于实际坝体填筑的复杂性,流变初始时间难以确定的问题。上述关系式中共包含α、b、d三个参数,故称之为三参数流变模型。
有限元应力应变分析中,为了在坝体应力应变分析过程中考虑流变变形引起的应变增量,需要通过以上流变试验成果整理出体积流变εVf以及剪切流变γf与应力之间的经验函数表达式。在三参数流变模型基础上,将堆石体流变变形的体积流变εVf和剪切流变γf计算公式修正为
(11)
式中:b、c、d、m1、m2、m3为模型参数;sl为应力水平;q为偏应力,kPa。
4 堆石料计算参数
对平寨水库面板堆石坝堆石料的瞬时弹性采用“南水”双屈服面弹塑性模型计算,该模型K、n、Rf、c、φ、Rd、cd和nd这8个参数,可由三轴试验整理得出,模型参数值见表1。混凝土面板、趾板按线弹性考虑,其重度γ=24.5kN/m3,弹性模量E=30GPa,泊松比μ=0.167。面板与堆石体中间采用Goodman单元模拟接触面,流变模型采用三参数模型,具体参数见表2。

表1 坝体填筑料计算参数

表2 流变模型计算参数
5 堆石流变对面板堆石坝应力变形的影响
平寨水库混凝土面板堆石坝三维有限元分析过程中,根据面板垂直缝共切取56个横剖面进行三维网格剖分。三维实体单元一般采用8结点六面体等参单元,坝体共形成三维实体单元12089个,结点14136个。大坝空间三维网格图见图4。通过河床最大剖面以及坝轴线纵剖面来描述坝体的变形特性,对于顺河向位移,以指向下游为正,指向上游为负;对于坝轴向位移,以左岸指向右岸为正,以右岸指向左岸为负;应力以压应力为正,拉应力为负。

图4 大坝三维网格图
5.1 流变对坝体变形的影响
考虑流变与不考虑流变计算成果的对比值见表3。考虑流变后竣工期和蓄水期的沉降都有明显的增大,分别为70.5cm和77.5cm,相应为坝高的0.45%和0.5%,与不考虑流变效应相比竣工期增加24.3%,蓄水期增加23.6%。并且运行20年后变形稳定期坝体沉降为85.7cm,为坝高的0.55%,较蓄水期增加了10.6%。顺河向考虑流变后变形表现为向坝内收缩,与不考虑流变计算结果相比,指向上下游向的水平位移均有所减小。坝轴线方向考虑流变后,轴向位移由两岸向河谷方向挤压严重,左岸向坡度较陡的右岸移动较大。因此,考虑流变后坝体沉降变形较大,变形持续时间较长。不考虑流变与考虑流变蓄水期的坝体变形见图5、图6。

表3 大坝变形计算成果对比 单位:cm
5.2 流变对面板应力的影响

图5 不考虑流变蓄水期坝体变形 (单位:cm)
表4给出了考虑流变与不考虑流变面板应力变形计算成果。考虑流变蓄水期面板的应力变形见图7,考虑流变蓄水期面板轴向位移与挠度见图8。受河谷形状的影响,河谷中上部面板受到较大的轴向压应力,两岸出现拉应力。考虑流变作用时,在蓄水时受拉区域有明显增加,面板的轴向应力和顺坡向应力均有较大幅度增大,尤其是河谷中上部面板坝轴向应力。蓄水期面板轴向压应力为10.1MPa,轴向拉应力为1.58MPa,面板顺坡向最大压应力为15.28MPa,比不考虑流变时分别增加9.8%、9.7%、8.2%。运行20年后,面板轴向压应力增加12.3MPa,轴向拉应力增加0.79MPa,面板顺坡向最大压应力增加2.4MPa。因此,堆石料流变对面板影响较大,考虑流变时,面板堆石坝运行期轴向压应力增幅较大,河谷段面板发生挤压破坏的可能性增大,周边面板发生拉伸破坏的可能性增大。

图6 考虑流变蓄水期坝体变形 (单位:cm)
坝轴线方向位移为岸坡段面板向河谷位移,变形最大值发生在面板顶部,考虑流变后面板顶部的轴向位移和挠度均有较大增加,蓄水期面板指向右侧和指向左侧的轴向位移分别为3.47cm和2.88cm,挠度为30.76cm,约为坝高的0.20%。运行20年后,指向右侧和指向左侧的轴向位移分别增大到8.32cm和7.35cm,挠度增大到38.18cm,约为坝高的0.25%。

表4 面板计算成果对比

图7 考虑流变蓄水期面板应力变形分布(单位:MPa)

图8 考虑流变蓄水期面板轴向位移与挠度分布图(单位:cm)
5.3 流变对面板周边缝和垂直缝的影响
考虑流变后周边缝三向变位和垂直缝张开量均有所增大,蓄水期和20年后三向变位最大值分别为:错动22.8mm和24.4mm;沉陷15.3mm和16.0mm;张开4.2mm和4.5mm。蓄水期和20年后面板垂直缝最大张开变形分别为3.9mm和4.1mm。考虑堆石流变后周边缝和垂直缝的开度总体变大,但变化幅度不大。
6 结 语
根据已建堆石坝的筑坝规律,结合堆石料的大型三轴试验,得出堆石料流变模型的计算参数,对黔中平寨水库混凝土面板堆石坝进行三维有限元应力变形分析,结果表明:堆石体流变特性对坝体变形影响比较明显。考虑堆石料流变特性后,坝体变形较大,变形持续时间较长,主要有坝体的沉降变形,坝体在顺河向和坝轴向的挤压变形;同时流变对大坝面板的轴向和顺坡向应力、止水缝变位等方面均有一定幅度的增大影响。尤其狭窄河谷对坝体和面板存在拱效应,河谷中上部面板受到较大的轴向压应力,两岸出现拉应力,并且堆石体流变特性对面板应力呈增大趋势。
因此,在坝体及面板应力理论分析和计算中应考虑流变特性的影响。狭窄河谷高混凝土面板堆石坝设计和实施过程中,应在理论研究成果的基础上加强工程措施:如合理选择筑坝材料,提高碾压填筑标准,减少坝体后期变形,并应加强在应力集中区域的安全设计;同时,在面板浇筑前设置较长的预沉降期,并设置面板永久水平缝等来减小面板被挤压破坏的可能。
