采用乘性RNN的雷达HRRP目标识别

徐 彬，张永顺，张 秦，王富平，郑桂妹

(1.空军工程大学 防空反导学院，陕西 西安 710051；2.西安邮电大学 通信与信息工程学院，陕西 西安 710121)

高分辨距离像(High Resolution Range Profile，HRRP)是宽带雷达信号获取的目标散射点子回波在雷达射线上投影的向量和的幅度波形。它反映了目标散射体的雷达散射截面积沿雷达视线的分布情况，包含有重要的结构特征。相比于SAR/ISAR图像，HRRP数据作为一维特征具有易获取、易存储、易运算等优点，获得了雷达目标识别领域(Radar Automatic Target Recognition，RATR)的广泛关注。

HRRP目标识别的核心在于提取可分性特征，大量学者对这一问题进行了深入研究[1-13]。文献[1]采用数据的频谱特征进行识别，用来解决平移敏感性。而文献[2]针对HRRP的平移敏感性提取了三种稳健特征，并设计了多特征融合的分类器。但这些方法过分依赖人为经验和对数据的认知，算法普适应较差。文献[3]采用了多任务稀疏学习方法进行统计建模，不同帧的HRRP样本能够通过共享帧间信息而产生相关性，使得模型能自动地从小样本中学习特征。文献[4]设计了一种多层自编码模型，通过设计目标函数使模型能自动地学习模型参数，并通过多层结构逐层地提取HRRP数据中的抽象特征。这些方法均通过模型自动学习参数实现精准的特征提取。但他们仅仅考虑了HRRP样本的包络信息，而没有考虑样本内部距离单元之间的时序相关性。文献[5]将HRRP样本转化为序列的形式，然后采用隐马尔科夫模型(Hidden Markov Model，HMM)对序列进行建模来提取样本距离单元间的时序关系。文献[6]采用循环神经网络模型(Recurrent Neural Network，RNN)对HRRP样本进行建模，模型通过相邻时刻隐层单元之间的转移矩阵传递时序信息，并采用注意机制将所有时刻的信息进行融合，输出样本的类别。为了考虑双向时序相关性，研究者将原始HRRP样本转化为前向和后向序列，并设计前向和后向长短期记忆(Long Short-Term Memory，LSTM)模型提取时序信息[7]。通过考虑时序相关性，这些算法能够更准确地对HRRP进行建模，提取可分性特征，进行有效的识别。但是，HRRP样本具有方位敏感性，当目标相对于雷达视线的姿态发生变化时，会导致散射点的相对径向距离发生变化，从而使得HRRP的包络发生较大变化。同时，对于不同方位角下的HRRP数据而言，其距离单元间的时序相关性也必然发生变化。

为了解决HRRP方位敏感性导致的时序相关性变化与参数固定模型不匹配的问题，笔者提出了一种乘性循环神经网络模型(Multiplicative Recurrent Neural Network，MRNN)对HRRP进行识别。首先，模型将HRRP样本转化为序列数据；然后该模型采用乘性的方式对不同序列数据自适应地选择对应参数，以便提取数据稳健的时序动态特征；最后采用投票的策略将时序信息进行融合，输出样本类别。基于实测数据的实验结果表明，该算法不仅能够提高识别性能，而且在一定程度上缓解了由方位敏感性引起的时序特征的变化。

1 基于MRNN模型的HRRP目标识别

采用乘性循环神经网络模型进行HRRP目标识别的过程主要包括三部分：将数据转化为序列形式，采用乘性循环神经网络进行特征提取以及采用投票机制对所有时刻的信息进行融合输出样本类别。

(1)

其中，d为滑窗的长度，b为相邻时刻输入数据重叠的距离单元，xt∈Rd×1为序列第t时刻的输入。经过滑窗处理，当前数据为x∈Rd×T，T为序列长度。其中，窗长和重叠单元会影响最终的序列长度，当序列长度过长时会对模型的传输信息能力要求较高，从而影响最终的识别性能；而当序列长度较短时，相邻输入数据的时序性较差，会导致模型的性能下降。

将HRRP样本转化为序列数据后，采用乘性循环神经网络模型对数据进行提取特征。图1展示了乘性循环神经网络模型的展开。从图中可以看出，模型主要包括三层，即数据输入层x，隐层特征层h以及类别输出层y。不同于传统的神经网络模型，循环神经网络模型在相邻的隐层时刻之间增加了权值系数Whh，通过该参数使得模型能够传递相关性信息。

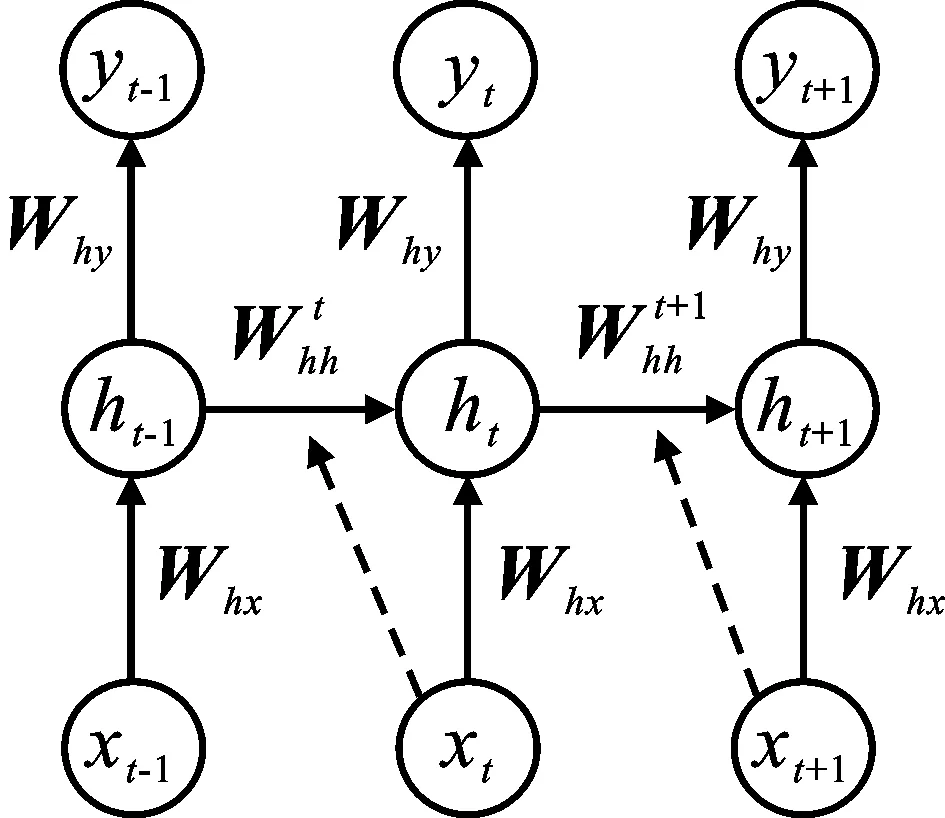
图1 乘性循环神经网络模型的结构图

对于输入序列x∈Rd×T，模型通过迭代的方式得到隐层特征，即

(2)

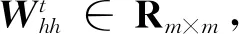
众所周知，HRRP数据具有方位敏感性，即不同方位角下的数据包络差异性较大，这使得其时序相关性也随之发生变化。而传统的循环神经网络模型中所有时刻的参数均是共享的，这使得模型不能有效地提取不同方位角HRRP数据的时序信息。为解决这一问题，张量循环神经网络模型被应用于HRRP识别中[11]。通过添加张量参数，模型能够根据输入数据自适应地选择模型参数，即

(3)

(4)

对于提取的隐层特征H=[h1，h2…，hT]，模型通过分类器将不同时刻的隐层输出样本类别。笔者采用soft-max分类器进行处理，即

(5)

其中，p(ytj|x，θ)对应于样本属于第j类的概率，wj∈R1×m为分类器中权值矩阵Why∈RK×m的第j行，K为样本类别个数，m为隐状态的维度，类别序列y=[y1，…，yT]。

不同于传统的序列数据输出类别序列，HRRP样本对应于单个类别。因此，笔者采用一种投票的策略将所有时刻的信息进行融合，输出样本x对应的类别。

(6)

(7)

(8)

其中，k*为样本对应的类别，zk指的是类别序列y中属于第k类的个数，Ot对应于xt所属的类别，ytk为xt属于第k类的概率，1(·)函数为当输入成立时等于1，而输入不成立时等于0。通过将所有时刻信息进行融合，乘性循环神经网络模型能够根据输入数据自适应地选择模型参数，精准提取不同方位角下HRRP时序信息，缓解了HRRP方位敏感性导致的包络变化问题，从而有效地提高了识别性能。

2 实验结果与分析

为了验证模型的有效性，笔者采用了国内某逆合成孔径雷达实测飞机的数据。该雷达的中心频率为5.5 GHz，带宽为400 MHz。三类飞机分别为安-26，奖状以及雅克-42，它们的飞行轨迹在地面上的投影如图2所示。

从图2中可以看出，三类飞机的飞行轨迹被分成多个数据段。为了验证模型的普适性，笔者在选取样本时主要按照两个原则：(1)训练样本和测试样本在不同段中；(2)训练样本基本覆盖所有方位向信息。选取安-26的5，6段，奖状的6，7段以及雅克-42的2，5段作为训练样本，其余段作为测试样本。其中，训练样本个数为7 800，测试样本个数为5 124，每个样本的维度D=256。样本均为时域数据，通过将样本取模值，并采用质心对齐的方式消除原始样本的幅度敏感性和平移敏感性。

为了验证当前算法(MRNN)模型的性能，将该算法同多种传统的HRRP目标识别进行对比，主要包括：最大相关系数法[13]，自适应高斯分类器[4]，隐马尔科夫模型[5]，深度置信网络模型[4]，除此之外，还展示了原始RNN模型6]以及张量RNN模型[11]的识别性能。对于MRNN模型，采用了adam算法进行模型参数的更新[12]，10个样本作为一个批次更新一次参数，所有的参数均采用标准差为0.1的高斯分布进行随机初始化。

为了分析模型参数对于识别性能的影响，分别比较了隐层维度和转移矩阵Whh的秩对于HRRP识别结果的影响。图3(a)展示了3种识别算法MRNN，TRNN以及RNN的识别性能随隐层维度的变化情况，其中MRNN模型中转移矩阵的秩为30。从图中可以看出，MRNN的性能随着隐层维度的提高略有提升，并逐渐趋于稳定，这是由于隐层维度的提高使得模型的自由度更高，更有利于提取特征，而当隐层维度达到一定程度后，模型趋于稳定。此外，从图中可以注意到，MRNN模型的性能在不同隐层维度下，识别性能均明显优于其他两种模型。为进一步分析转移矩阵的秩对于识别性能的影响，实验固定MRNN模型的隐层维度为50。图3(b)展示了MRNN模型的识别性能随秩的变化情况。从图中可以看出，识别性能随着秩的提高而逐渐增加，当达到30时处于峰值，而当秩再提高时性能逐渐下降。这是由于随着转移矩阵秩的提高，模型能够更准确地表达HRRP数据的时序性，当秩过高时，模型处于过拟合状态，使得测试数据的性能下降。因此，在后续的实验中将模型的隐层固定为50，秩为30。

(a) 安-26 (b) 奖状 (c) 雅克-42

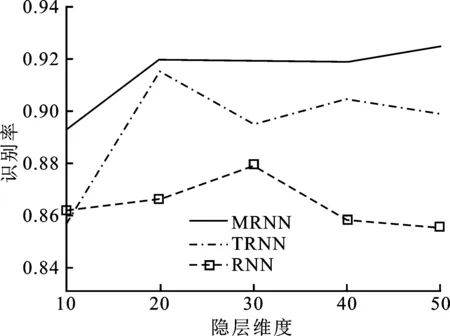
(a) 识别性能随隐层维度的变化情况

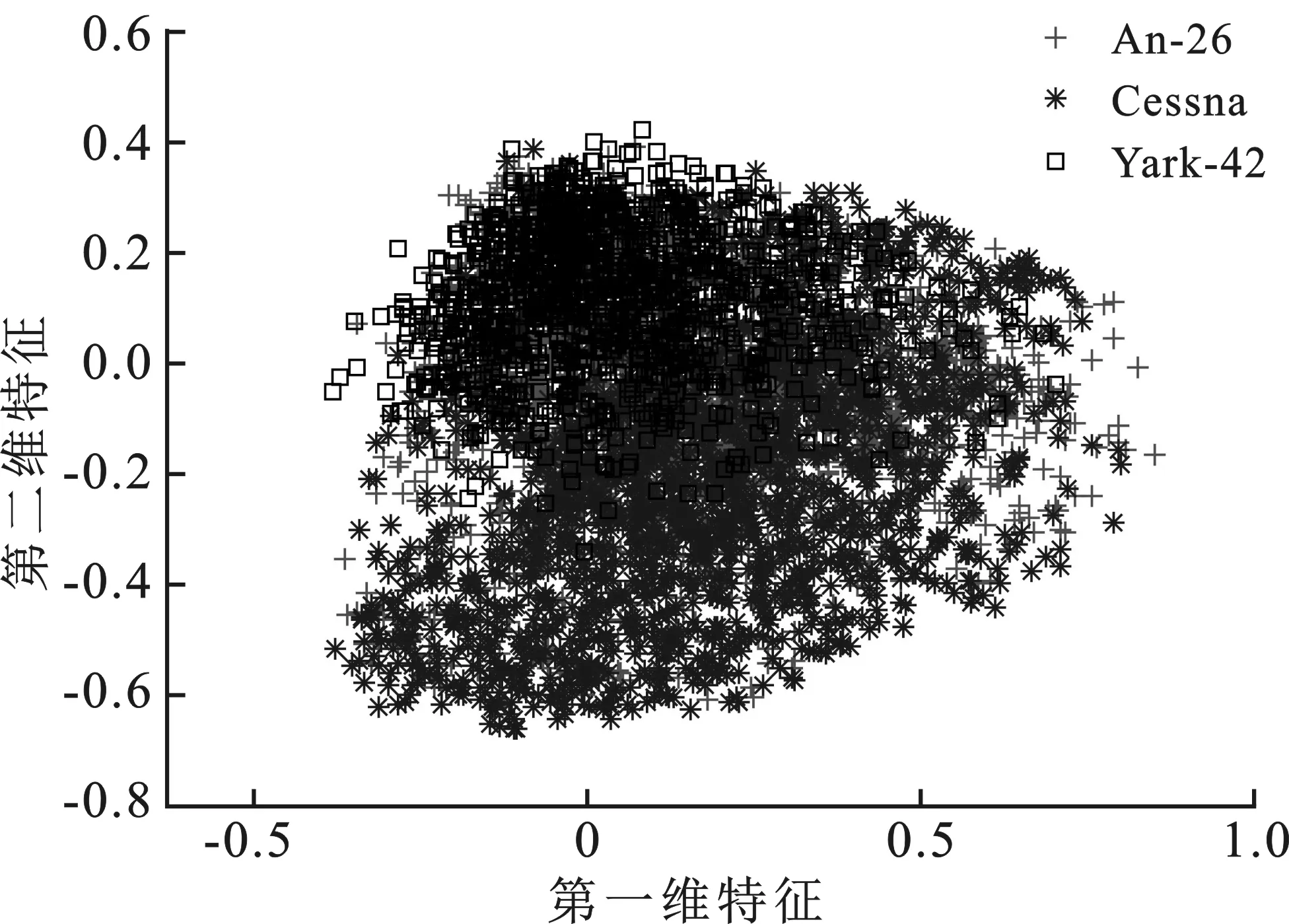
(a) 原始数据

表1展示了MRNN模型和不同HRRP识别方法的性能对比。从表中可以看出，通过考虑时序相关特性，RNN模型的识别性能要优于只考虑HRRP包络信息的DBN模型。TRNN模型通过加入张量参数使其能够根据输入数据自适应地选择对应参数，更有利于提取特征，识别性能要明显高于RNN模型。而文中提出的MRNN模型则进一步将TRNN进行改进，不仅降低了参数量，提高了运算效率，而且能够通过选择转移矩阵秩的维度，使模型的性能达到最优。

表1 MRNN和不同HRRP识别算法的结果对比

表2展示了RNN模型和MRNN模型的混淆矩阵以及平均识别性能，其中，混淆矩阵中每一列的和为1。从表中可以看出，MRNN模型性能的提高主要是由于奖状飞机的识别性能的提高。由于奖状飞机是小型喷气式飞机，相比于雅克-42和安-26，奖状飞机的包络起伏更为明显，当方位角发生变化时，时序性变化地更为剧烈。通过引入乘性参数，模型能够根据方位角的变化自适应地选择对应的参数，更准确地提取距离单元之间的时序相关性，提高识别性能的同时，对于方位敏感性也更为稳健。

表2 MRNN同RNN的混淆矩阵的识别性能

图4展示了原始数据和MRNN模型提取的特征的主成分分析(Principal Component Analysis，PCA)二维投影图。从图中可以看出，原始数据的投影点重合在一起，可分性较差。图4(b)分别用三种不同的结构表示MRNN模型提取的特征在二维平面上的投影。从图中可以看出，MRNN模型提取的特征的投影点重合部分较少，说明了当前模型提取特征具有可分性。

3 总 结

传统的HRRP识别算法没有考虑到其距离单元之间的相关性，且HRRP方位敏感性导致不同方位角下样本的时序相关性发生变化。为了解决这一问题，笔者提出了基于乘性循环神经网络模型(MRNN)的HRRP目标识别。该算法首先将HRRP样本转化为序列形式来考虑其时序相关性，并将转移矩阵同输入数据相关，使模型能够对不同的输入数据自适应地选择对应参数，提高了模型的表达能力，缓解了方位敏感性导致的时序相关性变化，最后采用投票策略将所有时刻的信息进行融合输出样本类别。基于实测数据的实验结果表明，当前的算法能够有效地提取可分性特征，提高了识别性能。