曲面拟合的GPS 高程转换研究
2021-04-29吴家杰刘锟铭
吴家杰 刘锟铭 黄 霞
(江西省煤田地质局测绘大队 江西南昌330001)
1 引言
在测量中,获取某地一高程时主要通过传统的水准测量或三角高程测量的方法,传统水准测量和三角高程测量法虽然在精度上可以达到要求,但是效率低,费用高,且要求点与点间互相通视。全球定位系统(GPS)具有全天时、高精度、高效率等优势,利用GPS 测量空间一点的空间位置是当前常用手段,但获取的高程是相对于WGS-84 椭球的大地高,其结果难用于工程测量中,需要将大地高转换为正常高才可运用于实际工作。
为了解决这一问题,国内外研究学者在GPS 高程转换研究中投入了大量精力,常用的GPS 高程转换法有数学模型法(即通过一些GPS 水准点来内插待求点)、重力测量法(即利用重力场模型来解求高程异常值)、联合平差法(即利用多种观测数据联合平差获取最优值)、神经网络模拟法。本文研究区域属于丘陵地区,在早期测量中拥有较多GPS 水准点且分布均匀,故本文运用较成熟的曲面拟合法将铅山区域GPS 高程点转换为正常高。
2 理论方法
2.1 GPS 测高基本理论
GPS 测量的高程是以WGS-84 椭球面为基准测量的大地高,工程测量常用的高程一般是以似大地水准面或大地水准面为基准的正常高或正高,如图1 所示即为参考面之间的相互关系[1]。我国采用的是以似大地水准面为基准的正常高系统[2]。
正高与大地高的关系如式(1)所示[3],正常高与正高的关系如式(2)所示,其中Hz代表正高、Hd代表大地高、Hzc代表正常高、N 是大地水准面差距、ξ 是高程异常。

图1 参考面之间的相互关系

2.2 曲面拟合法
曲面拟合法是工作中常用的拟合方法[4],要求控制点呈网状且均匀分布,根据已知资料特点,我们选择移动曲面法来拟合地表形态。移动曲面法是以待求点为圆心,选择半径为R 的区域进行搜索,根据选择区域内的已知点进行拟合,当搜索范围内的已知点数量不够时,则增大R 值来扩大搜索范围。移动曲面法所用曲面为二次曲面,当满足真实值与拟合值之差的平方和最小时,所求结果即为最优解,以下是移动曲面拟合法原理:
(1)建立局部坐标。设待求点坐标为(xi;yi),(i=1、2、3…n;n≥6),将待求点坐标改化到以P 点为原点的局部坐标中,如式(3)所示。

(3)列出误差方程式。选择二次曲面作为拟合曲面,式(4)即为拟合曲面误差方程式。

由n 个已知点列出的误差方程如式(5)。

(4)引入权值。由于每个GPS 水准点对待求点的影响不一,故引入权值来反映该点与待求点的相关程度,距离越小、对拟合结果贡献值越大。这里选择权为距离平方和的倒数,权的公式为pi=1/,其中di为GPS 水准点与待求点的距离。
(5)法化求解。根据平差理论,二次曲面系数的解为X=(XTPM)-1MTPZ,由于X′P=0,Y′P=0,即移动多项式的常数项为内插计算的内插值。
3 实验与分析
本次实验选取江西省上饶市铅山县全县区域为研究对象,铅山县自然资源局于2017 年曾开展“铅山县行政区域内1:1000 航测服务项目”,项目其中一项工作是全县GPS 静态E 级控制点布设并施测高程。本次实验数据采用的是全县GPS 静态D 级和E 级控制点,控制点布设均匀,其中D 级GPS 点28个,E 级GPS 点46 个,四等水准测量144 千米。

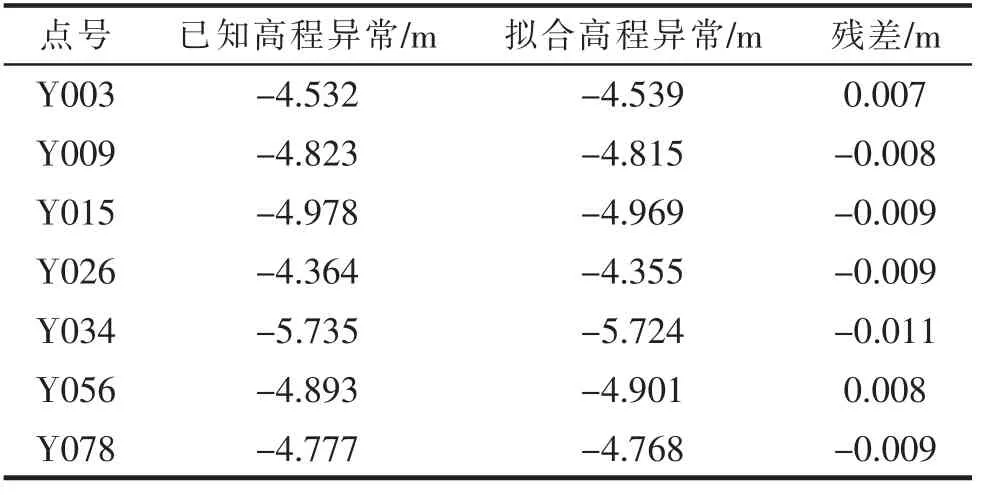
表1 检核点高程异常值对比
4 结束语
本文介绍了GPS 测高基本理论二次曲面拟合法,结合铅山县实际情况,选取了移动曲面拟合法对铅山县GPS 高程转换进行研究。实验证明,移动曲面拟合法计算的GPS 高程可替代四等水准测量。研究成果可应用于工程测量,可减少人力物力的投入,具有推广意义。
