江门市高精度GNSS控制网数据处理技术研究
2021-04-29涂纯二江翠云陈国恒
涂纯二,江翠云,陈国恒
(1.广东省国土资源测绘院,广东 广州 510500;2.广东省测绘工程公司,广东 广州 510000)
我国未来大地基准重点发展方向集中在2000 中国大地坐标系(CGCS2000)的建立与维持、高程基准现代化、兼容北斗的全球导航卫星系统(GNSS)多源数据融合、大地参考框架维持以及多源技术集成的空天参考基准一体化方面[1],而CGCS2000 是基于国际参考地球框架ITRF97,并定义在2000 历元下的坐标[2]。近年来,华南沿海地区包括广州[3]、珠海[4]、惠州[5]、桂林[6]、三明[7]、海口[8]等城市为响应国家统一使用2000 国家大地坐标系的要求,纷纷建立符合现代化测绘地理信息发展的测绘基准框架。本文以华南沿海城市江门作为应用实例,从建设高精度的2000 国家大地坐标系GNSS 控制网数据处理方面进行技术探讨,通过基线解算与网平差计算的策略优化,以获取高精度的GNSS 大地基准成果,为华南沿海地区的高精度现代化大地基准建设提供借鉴参考。
1 项目概况
江门市大地基准控制网分为G N S S 框架网(GNSS-B 级)与基本网(GNSS-C 级)。框架网由12 个GDCORS 基准站与15 个框架点构成,利用到的GDCOR 基准站有佛山更合站(FSGH)、恩平站(GDEP)、上川站(GDSC)、阳江站(YJGT)、台山站(GDTS)、新兴站(GDXX)、阳春站(GDYC)、高明站(GMGT)、江门站(JMGT)、金湾站(JWGT)、顺德站(SDGT)、中山站(ZSGT)。基本网由江门站(JMGT)、恩平站(GDEP)、阳江站(YJGT)、15 个框架点、140 个基本点组成。
项目结合华南沿海地区的地理环境特点,在满足规范基本要求的基础上,通过基线解算与网平差计算两方面的策略进行分析,以提高数据处理的精度。
框架网外业采样间隔由规定的30 s 缩减至10 s,基本网的外业采样间隔由规定的10~30 s 缩减至5~10 s,并以基本网的其中一个时段作为分析,分别使用30 s 与5 s 的采样间隔进行数据解算,分析其精度影响,以此来调整项目的基线解算策略。
2)基本网的观测时长增加至20 h 以上,并以其中一个时段作为分析,分别使用8 h 和20 h 进行数据解算,分析其精度影响,以此来调整项目的基线解算策略。
3)数据处理采用高精度的数据处理专用软件,其中基线解算采用GAMIT,网平差计算采用PowerNet或GLOBK,通过平差精度上的对比分析,以此来调整项目的网平差计算策略。
2 数据处理
2.1 基线解算分析
为研究分析本项目在基线解算上的策略,在使用GAMIT 进行基线解算时,保证以下考虑因素不变的条件下[9],再对采样间隔及观测时长进行调整解算。
1)卫星钟差的模型改正(用广播星历中的钟差参数);
2)换收机钟差的模型改正(用根据伪距观测值计算出的钟差);
3)电离层折射影响用LC 观测值消除;
4)对流层折射。框架网根据标准大气模型用萨斯坦莫宁(saastamoinen)模型改正,采用分段线形的方法估算折射量偏差数;基本网测站间距离较短、且观测时气候状况稳定,因此考虑不估计对流层天顶延迟,采用双差的方法来消除对流层延迟;
5)卫星和换收机天线相位中心改正,换收机天线L1、L2 相位中心偏差采用设定值;
6)测站位置的潮汐改正采用FES2004 模型;
7)框架网截止高度角为10°;基本网截至高度角为15°。
针对基线解算中的采样间隔选择,本文选取了基本网的第299 个年积日的时段数据,观测时长为8 h,基线解算采样间隔分别设置为30 s 和5 s,分别从N、E、U 各基线分量精度进行比对分析,见图1。

图1 采样间隔对基线精度的影响分析
由图1 可以看出,当选择5 s 的采样间隔时,N、E、U 分量的基线精度均优于选择30 s 的采样间隔。其中5 s 采样间隔N 方向精度在0.002 3 ~0.006 1 m 之间,平均精度为0.003 6 m;30 s 采样间隔N 方向精度在0.004 2 ~0.008 2 m 之间,平均精度为0.005 5 m;5 s 采样间隔使N 方向基线精度较30 s 平均提高了35.10%。5 s 采样间隔E 方向精度在0.002 6~0.007 3 m之间,平均精度为0.004 0 m;30 s 采样间隔E 方向精度在0.003 4~0.006 7 m 之间,平均精度为0.005 0 m;5 s 采样间隔使E 方向基线精度较30 s 平均提高了19.74%。5 s 采样间隔U 方向精度在0.003 8~0.010 6 m之间,平均精度为0.006 1 m;30 s 采样间隔U 方向精度在0.006 6~0.014 7 m 之间,平均精度为0.010 4 m;5 s 采样间隔使U 方向基线精度较30 s 平均提高了41.69%。因此,可选用较小采样间隔方案作为本项目的解算策略。
针对基线解算中的观测时长选择,本文同样选取了基本网的第299 个年积日的时段数据,采用间隔设置为10 s,分别将观测时长设为8 h 和20 h 进行基线解算,分别从N、E、U 分量精度进行比对分析。比较分析见图2。

图2 观测时长对基线精度的影响分析
由图2 可以看出,当选择20 个小时观测时长时,N、E、U 分量的基线精度均优于选择8 h。其中20 h 观测时长N 方向精度在0.001 5~0.003 8 m 之间,平均精度为0.002 3 m,8 h 观测时长N 方向精度在0.002 4~0.005 8 m 之间,平均精度为0.003 5 m,20 h观测时长使N 方向基线精度较8 h 平均提高了34.49%;20 h 观测时长E 方向精度在0.001 7~0.004 3 m 之间,平均精度为0.002 5 m,8 h 观测时长E 方向精度在0.002 2~0.005 2 m 之间,平均精度为0.003 3 m,20 h观测时长使E 方向基线精度较8 h 平均提高了22.95%;20 h 观测时长U 方向精度在0.002 4 ~0.006 8 m 之间,平均精度为0.003 8 m,8 h 观测时长U 方向精度在0.003 9 ~0.011 9 m 之间,平均精度为0.006 6 m,20 h 观测时长使U 方向基线精度较8 个小时平均提高了41.74%。因此,基本网可选用20 h 或以上的时观测时长方案作为本项目的解算策略。
采用上述两种优化后的策略进行本项目框架网和基本网的基线解算,并对基线重复性和闭合环进行检验。框架网与基本网共构成4 745 个闭合环,闭合差为0.004 9 m,基线重复性检验统计如表1 所示,两者均满足规范与项目设计要求。

表1 基线重复性检验
2.2 网平差计算分析
本项目选择我国自主研发的PowerNet 与美国麻省理工(MIT)和美国加利福尼亚大学SCRIPPS 海洋研究院(SIO)共同开发的GLOBK 软件[10]进行网平差计算。通过比较两套平差软件在平差结果上的精度,以此来调整本项目的网平差计算策略。
在数据处理过程中,通过采用PowerNet 软件进行无约束平差,发现JWGT 与其他站点不兼容,且与已知起算坐标值X方向差为4 cm,Y方向差为9 cm,Z方向差为4 cm,因此,将JWGT 仅作为待求点参与基线解算,不作为起算点进行平差计算。本次实验中以FSGH、GDEP、GDSC、YJGT、GDTS、GDXX、GDYC、GMGT、JMGT、SDGT、ZSGT 共11 个GDCORS 站点作为起算,其成果为2000 国家大地坐标成果(坐标框架为:ITRF97,历元为2000.0),平差得到各框架点与基本点在CGCS2000 框架下的坐标成果。
使用PowerNet 软件与GLOBK 软件以上述11 个GDCORS 站进行约束平差,分析比较平差结果文件中N、E、H 方向上的精度,如图3 所示。

图3 平差精度比较
通过图3 比较PowerNet 与GLOBK 平差后的精度,PowerNet 软件在N、E 方向上平差精度均在6 mm 以下,H 方向上平差精度(排除粗差点JWGT)均在10 mm 以下,平差精度良好;而GLOBK 相比与PoweNet 软件,在N、E、H 上其总体平差精度在N、E、H 方向上均更高。PowerNet 平差精度平均值为2.590 mm,GLOBK 平差精度平均值为0.937 mm,较PowerNet 平均精度提高了63.81%;在E 方向上,PowerNet 平差精度平均值为2.776 mm,GLOBK 平差精度平均值为1.007 mm,较PowerNet 平均精度提高了63.74%;在H 方向,PowerNet 平差精度平均值为4.953 mm,GLOBK 平差精度平均值为1.969 mm,较PowerNet 平均精度提高了60.24%。由此可见,使用GLOBK 软件进行本项目框架网与基本网的整体平差,其平差精度在N、E、H 上均优于PowerNet 软件,可选用GLOBK 作为本项目的网平差计算软件。最终选用GLOBK 软件进行网平差计算得到CGCS2000 坐标成果,点位精度统计见表2。
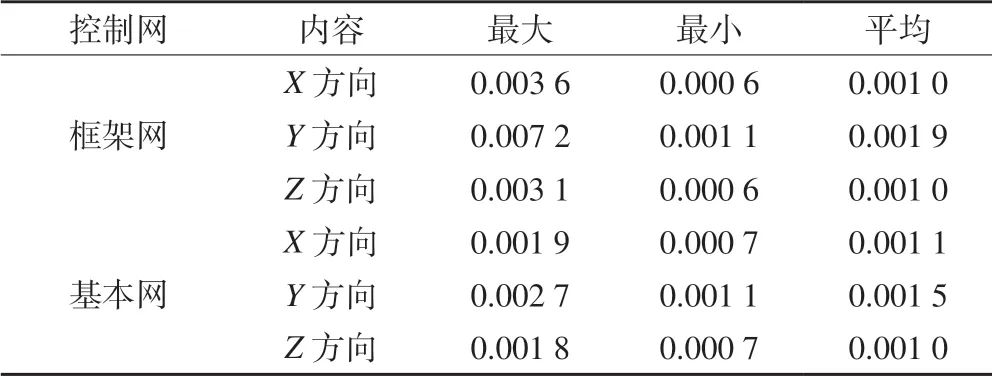
表2 点位精度统计/m
3 结 语
本文以华南沿海城市江门作为应用实例,从建设高精度的2000 国家大地坐标系GNSS 控制网数据处理方面进行技术探讨,通过基线解算与网平差计算的策略优化,得到以下几点结论。
1)框架网与基本网的基线处理采用GAMIT 软件,通过设置较小的采样间隔,以及基本网采用更长时间(20 h 以上)的观测时长,使在数据处理中获得更高的基线解算结果。将此基线解算策略应用于整网的数据处理,其基线重复性和闭合环检验均满足规范与项目设计的要求。
2)通过比较PowerNet 与GLOBK 两款高精度的平差软件,最终选择GLOBK 应用于本项目的网平差计算,得到该地区在CGCS2000 框架下的三维大地坐标基准。
3)高精度控制点坐标为今后基础测绘基准的最终建立提供了科学的依据,也可为高精度、高分辨率似大地水准面的建立提供均匀、可靠和精确的数据。
