网联通信时延下的混合队列控制特性分析*

许 庆 王嘉伟 王建强 李克强 高博麟

（清华大学车辆与运载学院 北京100084）

0 引 言

由于道路瓶颈和行车不确定性的存在，以车辆速度波动为主要形式的交通扰动会在交通流中不断产生[1]。在驾驶员反应时间长、感知范围小等特性的影响下，这些扰动在交通流中可能会被持续放大和不断累积，并最终导致交通激波的出现[2]，这一现象被认为是交通拥堵产生的重要原因。基于车联网和自动驾驶技术的智能网联汽车（intelligent and connected vehicle，ICV）的诞生克服了驾驶员驾驶车辆的缺陷，被广泛认为能给当今交通系统带来革命性改变[3-4]。

队列控制是ICV 的代表性技术，其中自适应巡航控制（adaptive cruise control，ACC）和协同自适应巡航（cooperative adaptive cruise control，CACC）是2 个典型案例。一般意义上，ACC 依赖于自车传感器获取与前车的相对距离与相对速度，从而进行跟车决策；而CACC 从ACC 拓展而来，增加了车车通信（vehicle-to-vehicle,V2V）等网联化手段获取其他车辆的加速度等信息，并基于此设计ICV 的跟车策略，提升自车跟车性能。大量研究均表明，上述技术能极大地提升交通效率，改善行车安全，以及降低燃油消耗[3-4]。

但传统的队列控制技术多针对所有车辆全部自动驾驶的工况，在实际的智能网联汽车技术推广过程中，势必会存在1个长期的过渡阶段，即智能网联汽车与驾驶员驾驶汽车（human-driven vehicle，HDV）共存的混合队列工况[5]。研究2 类汽车共存的混合队列系统，对于理解智能网联汽车对交通系统的影响、评价智能网联汽车技术的性能、制定智能网联汽车推广政策等等具有深远的意义。国内外已有部分研究从不同的角度对混合队列系统进行了一定的探索。例如，大规模交通仿真实验通常会发现，智能网联汽车需要达到一定的市场渗透率（market penetration rate，MPR）才能对交通系统产生明显提升[6-10]；Stern等[5]通过实车实验指出了智能网联汽车在极低渗透率下镇定交通流的可能，这一可能性随后被Zheng等[11]、Wang等[12]进行了理论上的证明，从而揭示了设计混合队列场景下的智能网联汽车特殊控制策略的潜能。上述研究一般会假设理想的车联网通信条件，但在实际应用过程中，往往会存在通信时延等非理想通信因素[13]，这些因素对于混合队列性能的影响尚不明确。

针对上述问题，笔者重点探讨网联通信时延影响下的，由CACC 控制的智能网联汽车与驾驶员驾驶汽车构成的混合队列系统的性能。首先，介绍CACC设计方法；随后，分析CACC系统和通信时延过长导致的退化后的ACC 系统的队列稳定性（string stability）；接着，搭建仿真场景，进行大规模交通仿真实验；最后，分析无时延的CACC、有时延的CACC、退化后的ACC在不同渗透率下的交通激波（traffic shockwave）特性。

1 协同自适应巡航控制方法

由于加速度信号通过V2V通信获取，因此可能存在一定的通信时延，假设时延量为θ（单位：s），则在前馈控制之前还存在时延环节D(s)=e-θs。综合上述各环节，从而得如图1（b）的CACC控制器系统框图。

图1 协同自适应巡航控制系统（CACC）Fig.1 Cooperative adaptive cruise control（CACC）

需要注意的是，当θ充分大时，即通信时延很大时，为保障跟车可靠性，往往会将CACC退化到仅依赖自车传感器进行跟车的ACC控制系统，即不再有前馈控制环节，F(s)=0。

2 队列稳定性分析

队列稳定性反映了自车抑制前车扰动的能力，是微观跟车层面反映车辆控制性能的重要指标。基于所设计的CACC 系统，在无时延CACC、有时延CACC 和退化后的ACC 这3 种情况下，讨论各自的队列稳定条件。

2.1 队列稳定性条件求解

队列稳定性的1种判定条件如下：定义第i辆车位移相关的队列稳定传递函数为[17]

2.2 队列稳定性条件数值验证

上述考虑通信时延下的队列稳定最小跟车时距式（23）为1 个近似解析解，下面通过数值求解分析其与真实数值解之间的误差，并分析通信时延对其数值的影响。

令车辆动力学模型（2）中的时间常数η=0.1，取反馈控制器K(s)中的2 组参数，见表1。在不同的通信时延量下（θ∈(0，0.5]s），利用Matlab对式（13）进行数值求解，解出队列稳定最小跟车时距的数值解，与式（23）求出的近似解析解进行对比。数值解与解析解在不同通信时延下的图像绘制见图2。

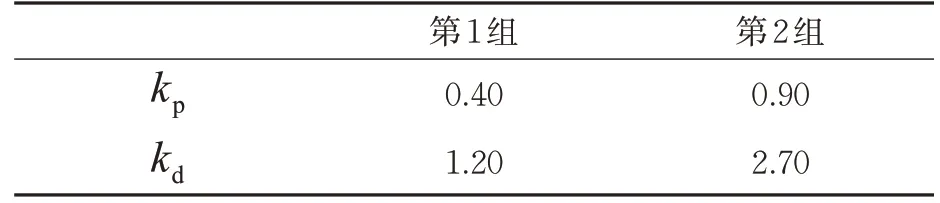
表1 反馈控制K( s )的参数取值Tab.1 Parameter setup for the feedback K( s)

图2 不同通信时延下的队列稳定最小跟车时距Fig.2 Minimum time headway for string stability at different communication delays

图2中，实线表示数值解，虚线表示解析解，2种不同的颜色代表2组控制器参数。从图像中可以看出，要满足队列稳定的实际最小跟车时距比近似解析解的数值更大，但相差的值有限。在所采取的2组控制器参数下，理论解析解与真实数值解的差值处于0.05～0.10 s之间。可以认为，在非理想通信下求解出的队列稳定最小跟车时距，即式（23），具有一定可靠性。

此外，图2 也明确反映了通信时延对CACC 系统抗扰动性能的影响关系，随着通信时延增大，CACC 系统所需的队列稳定最小跟车时距迅速增大。需要注意的是，在2组控制参数下，由式（25）得到的退化后的ACC 系统的队列稳定最小跟车时距分别为2.24 s 和1.49 s，均大于图2 中所展示的CACC 系统在通信时延达到0.5 s 下的队列稳定最小跟车时距，这一结果说明，即使受到了通信条件的一定影响，基于车联网的CACC 系统相比于仅依赖于自车传感器的ACC 系统依然能显著提升智能网联汽车的抑制交通扰动的能力。

表2 头车运动轨迹Tab.2 Velocity profile of the leading vehicle

3 混合队列仿真分析

交通瓶颈是引起交通流扰动、导致交通拥堵的重要因素，其可能由交叉路口、车道减少、匝道汇入、交通事故等一系列事件产生。据现有文献结论[6-8]，为重现交通瓶颈的现象，可以采取单车道中头车受较强的外部扰动的方式，并通过车辆轨迹数据，分析交通激波的传递，从而分析交通扰动对交通流的影响。本小节通过交通仿真，从宏观层面的交通激波传递特性分析无时延CACC、有时延CACC 和退化后的ACC这3种情况的混合队列性能。

3.1 仿真场景布置

布置单车道仿真场景见图3。道路总长2 km，共有1辆头车（灰色车辆）及200辆跟随车辆，跟随车辆中包含驾驶员驾驶汽车（绿色车辆）以及智能网联汽车（蓝色车辆）。智能网联汽车所占的比例由其市场渗透率MPR 决定，图3中的情形仅为示意。针对市场渗透率，考虑MPR ∈{0.0,0.2,0.4,0.6,0.8,1.0} 这6种情形。针对每一渗透率下的智能网联汽车空间分布，保证从编号i至i+4(i=5k,k∈[1,39] 且k∈N)这5 辆车中，有5 ⋅MPR 辆智能网联汽车，以避免智能网联汽车随机分布导致的可能影响。

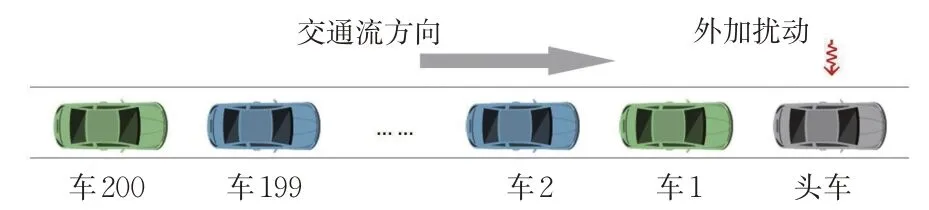
图3 仿真场景布置示意图Fig.3 Simulation scenario

考虑各车辆匀质的情形，即每一辆车具有相同的初始速度以及期望时距，车辆之间的初始间距为初始速度与期望时距的乘积。在仿真的前30 s内，不采取任何的外加干扰，让头车以初始速度匀速行驶，让200 辆跟随车辆在或驾驶员模型或队列控制系统的作用下达到稳定跟车状态。在仿真进行到30 s 之后，开始对头车引入外部干扰的作用。仿真总时长为200 s。对于外部干扰，假定头车在30 s时开始紧急制动，接着保持低速行驶，最后恢复至初始速度，具体运动轨迹见表2。

对于各个跟随车辆，智能网联汽车采用本研究设计的CACC 进行控制，驾驶员驾驶汽车利用IDM+模型进行描述[7,18]。IDM+模型中，车辆的加速度由式（26）决定。

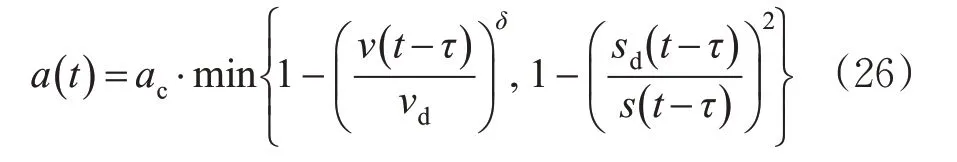
式中：ac为驾驶员舒适加速度，m/s2；vd为驾驶员期望速度，m/s；sd为驾驶员期望车头间距，m；s为当前车头间距，m；δ为自由加速度指数；τ为驾驶员反应时间，s。驾驶员期望车头间距sd满足

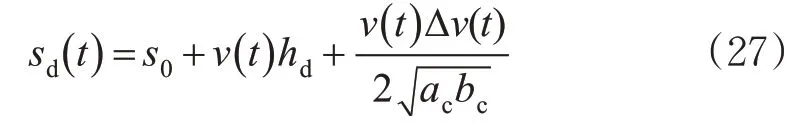
式中：s0为静止时的车距，m；hd为驾驶员期望车头时距，s，其与智能网联汽车的取值一致；bc为驾驶员舒适减速度，m/s2；Δv为自车与前车的速度差，m/s。各参数的具体数值见表3。

表3 交通仿真中的参数取值Tab.3 Parameter setup in traffic simulation

3.2 仿真结果与分析

为分析交通扰动在交通流中的传递，即交通激波的传递现象，现有研究常通过车辆轨迹数据进行分析，绘制所有车辆的时空轨迹图，随后通过车辆加速度[7]或车辆速度[8]反映交通激波，本文接下来也采用这2种方式进行分析。

情形1：所有车辆均为HDV时的实验结果分析。

首先考虑所有车辆均为驾驶员驾驶车辆的情形，即智能网联汽车渗透率MPR=0%的情形，结果见图4。图4（a）采用的是通过车辆速度进行区分交通激波的方法，红色越深表示车辆速度越低，蓝色越深表示车辆速度越大，速度低于期望速度25 m/s的区域即反映了激波影响的区域。从图中可以看出，当头车出现表2的扰动之后，在交通流中出现了2个交通激波：1 个向上游传播，1 个向下游传播，且2 个激波都没有明显消散的迹象。这说明交通流的后续车辆经历了2 次减速加速的过程，交通流产生了不稳定的振荡现象。

图4（b）采用的是通过车辆加速度进行区分交通激波的方法，当车辆出现a(t)＜-1 m/s（2即制动强度大于1 m/s2）时，认为该车辆受到了交通激波的影响。图4（b）中，灰色部分表示车辆加速度a(t)＞-1 m/s2，红色部分表示a(t)＜-1 m/s2，红色区域即反映了交通激波的传递。由图（1）可见：存在1个激波持续向上游传播，不会消散，这说明所有车辆均会经历1次强制动的过程；另外存在1 个较小的激波向下游传播，说明部分车辆会经历2次强制动的过程。

情形2：无时延CACC控制下的实验结果分析。

之前的实验结果反映了所有车辆均为驾驶员驾驶情况下的交通扰动持续传递且难以消散的现象，接下来考虑在不同渗透率下智能网联汽车采用CACC控制的实验结果，并假设通信时延θ=0 s。

在以速度区分交通波的情况下（见图5），可观察到的现象如下：①当渗透率达到20%及以上时，均只会产生1个交通激波，且最终会被消散；②随着渗透率的增大，低速区域的影响程度不断减弱，极低速区域的范围不断减小，即速度降至很低的车辆数目不断减少，交通效率得到提升；③离头车越远的车辆，受波动影响的程度越小，速度变化趋于缓和，说明驾驶舒适性得到了改善。

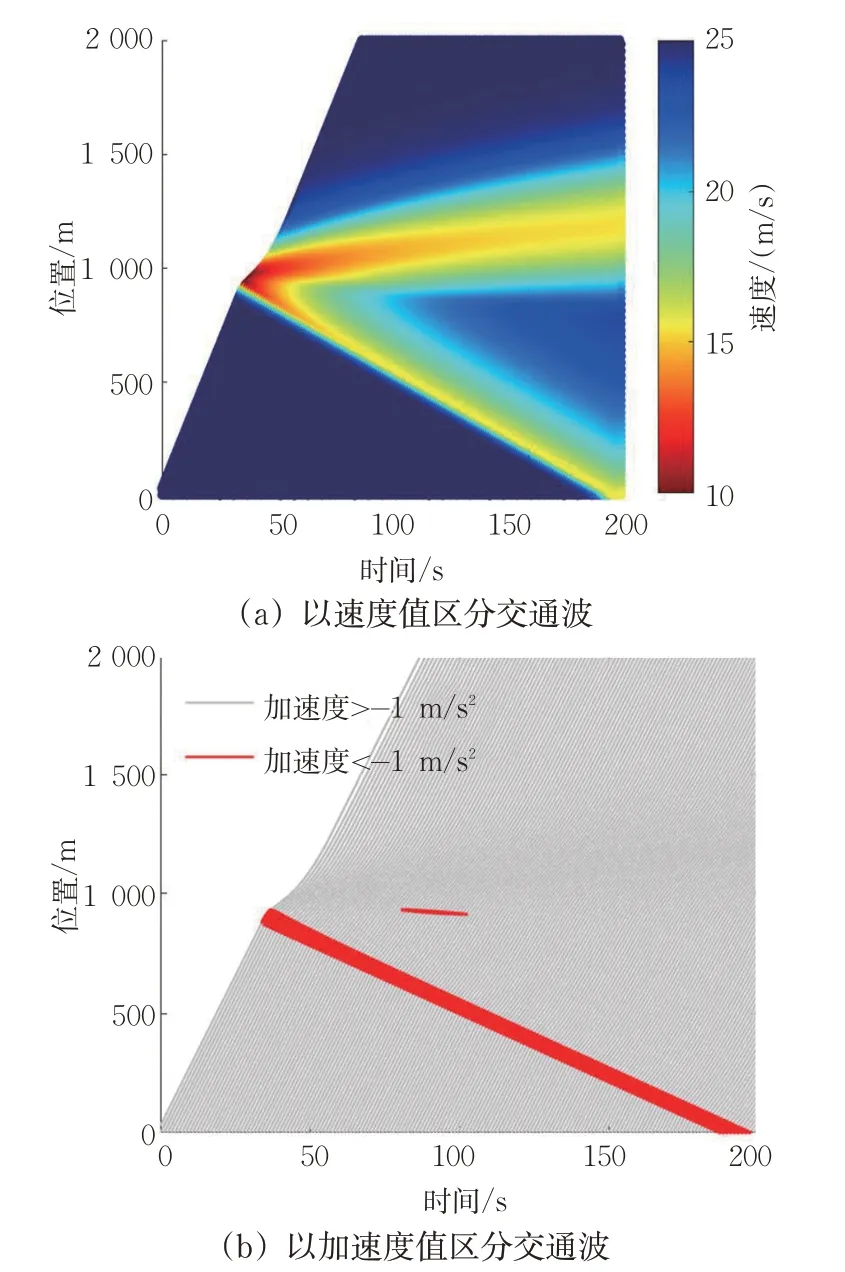
图4 所有车辆均为驾驶员驾驶汽车下的车辆轨迹图Fig.4 Vehicle trajectories when all the vehicles are human-driven

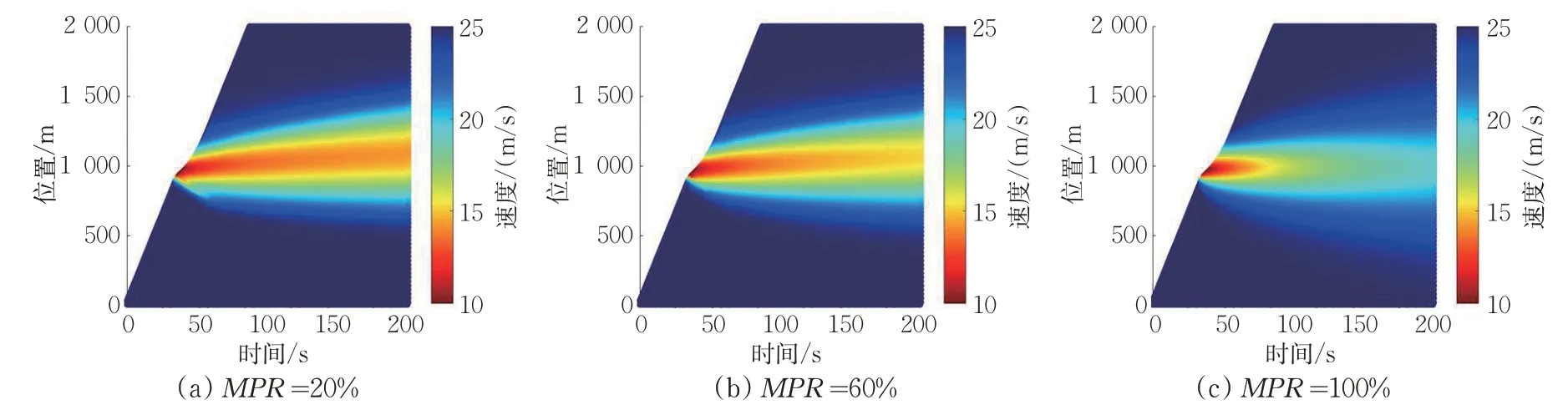
图5 通信时延θ=0 s时CACC控制下的车辆轨迹数据图（以速度区分交通波）Fig.5 Vehicle trajectories under CACC when θ=0 s（traffic wave is characterized by the velocity）

图6 通信时延θ=1 s时CACC控制下的车辆轨迹数据图（以速度区分交通波）Fig.6 Vehicle trajectories under CACC when θ=1 s（traffic wave is characterized by the velocity）

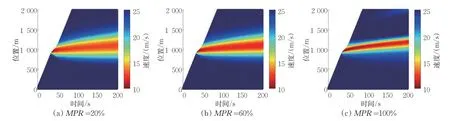
图7 退化为ACC控制下的车辆轨迹数据图（以速度区分交通波）Fig.7 Vehicle trajectories under ACC degraded from CACC（traffic wave is characterized by the velocity）

图8 通信时延θ=0 s时CACC控制下的车辆轨迹数据图（以加速度区分交通波）Fig.8 Vehicle trajectories under CACC when θ=0 s（traffic wave is characterized by the acceleration）

在以加速度进行区分的情况下（见图8），可观察到的现象如下：①当渗透率达到20%及以上时，交通激波会被明显消散，出现强制动现象的车辆局限在离扰动较近的部分车辆中，后续的跟随车辆不会再出现强制动的行为；②随着渗透率的增大，激波影响范围越来越小，持续时间越来越短。

相比于所有车辆均为驾驶员驾驶的情形，引入CACC控制的智能网联汽车之后，在低渗透率（例如20%）下交通流的抗扰动能力就得到了明显的改善，且随着渗透率的增加，扰动的影响越来越小，交通性能不断提升。

情形3：通信时延影响下的实验结果分析。

上述CACC 的实验并未考虑通信时延的影响，下面分析通信时延存在后，混合队列性能的变化。图6和图9展示了通信时延θ=1 s 时的仿真结果，可以看出，相比于无时延下的CACC控制（见图5与图8），整体交通流的抗扰动能力并未受到通信时延的明显削弱，交通波的影响范围略有扩大，持续时间略有上升，但总体保持了情形2的结果。

但当通信时延很大甚至通信信号丢失时，为保障控制效果，考虑CACC 退化后的ACC 控制策略，结果见图7与图10。可以看出，退化后的ACC控制相比于CACC产生了明显的不同，具体表现如下。

从速度角度区分（见图7）：①当渗透率达到20%及以上时，只会产生1 个激波，随着渗透率的升高，低速区域的范围越来越窄，持续时间越来越短；②但交通激波无法被完全消散，每辆车都会经历在短时间内迅速减速到极低速，又快速加速至原有速度的情况，且随着渗透率增加，速度变化的剧烈程度上升，影响了驾驶舒适性和安全性。

从加速度角度区分（见图10）：①当渗透率达到20%及以上时，交通激波会被明显消散；②但随着渗透率的增加，交通激波的影响范围不会越来越小，传递方向反而可能发生改变，从向上游传播（见图10（a）），变为固定的驻波（见图10（b）），最终变为向下游传播（见图10（c））。

综合情形3 的结果可知，当通信时延在一定范围内时（例如图6和图9展示的θ=1s的情形），通信时延对整体交通流的抗扰动性能影响较为有限，CACC 的引入依然显著提升了整体交通流的性能。若发生过大的通信时延或丢失通信信号，以致CACC退化至ACC系统后，尽管优于所有车辆均为驾驶员驾驶的情形，但相比于CACC控制下的情形，整体交通流的性能发生了明显的下降，ACC对交通效率、驾驶舒适性等性能的提升能力明显逊色于CACC的效果。

对比本研究中所考虑的ACC 系统和CACC 系统，二者的根本区别在于是否有基于前车加速度信号的前馈控制环节。上述仿真结果反映了该环节的重要性，通过网联通信，智能网联汽车可以获得其他车辆更丰富的信息，从而做出更有效的决策。即使存在一定的通信时延，该环节的引入也能帮助智能网联汽车实现对交通性能的进一步显著提升。

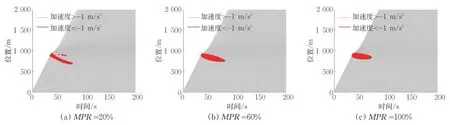
图9 通信时延θ=1 s时CACC控制下的车辆轨迹数据图（以加速度区分交通波）Fig.9 Vehicle trajectories under CACC when θ=1 s（traffic wave is characterized by the acceleration）

图10 退化为ACC控制下的车辆轨迹数据图（以加速度区分交通波）Fig.10 Vehicle trajectories under ACC degraded from CACC（traffic wave is characterized by the acceleration）

4 结束语

本文针对CACC 控制的智能网联汽车与驾驶员驾驶汽车构成的混合队列系统，分析了其在通信时延影响下的控制性能。从微观跟车行为的队列稳定性角度，本文求解了CACC 系统在不同通信时延条件下的队列稳定最小跟车时距，并指出其随时延增大而增大的特性。此外，也设计了大规模交通仿真实验，从整体交通流的交通激波传递现象角度，揭示了混合队列中CACC 相比于退化后的ACC，具有在一定时延范围内显著降低交通扰动、削弱交通激波的能力。考虑到近年来出现的新型的智能网联汽车队列控制技术，研究这些技术在通信时延影响下的混合队列性能，并与CACC 技术进行对比，是下一步需要开展的工作。