极值理论在重金属污染土壤修复中的应用

郭 兵，杨 庭，肖成磊，王永林

(中海石油环保服务(天津)有限公司，天津 300457)

引 言

由于重金属在土壤中的理化性质比较稳定且迁移性比较差，通过微生物或者其他手段无法将重金属降解，因此，重金属会在土壤中停留相当长的时间，累积到一定程度超过土壤的承载能力会破坏土壤结构[1]，影响土壤理化性质和土壤中的微生物群落[2]。随着工业社会的发展，重金属对环境的污染程度越来越得到重视，重金属可对自然环境和人体健康带来损害[3～5]。环境中的各种重金属来源[6]如表1所示，工业土壤中重金属污染场地以As、Pb、Cd、Cr污染最为典型[7]。

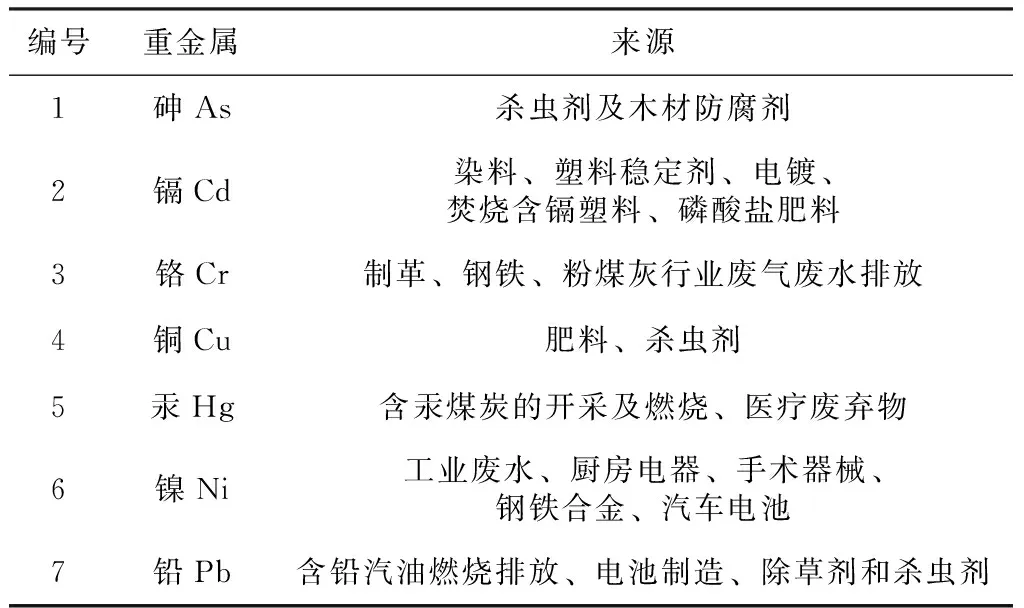
表1 环境中重金属污染来源Tab.1 Source of heavy metal pollution in the environment

对于重金属污染地块来说，重金属修复技术的适用性是影响修复效果的关键因素[8]，重金属修复技术的筛选需要以场地条件、修复目标、修复要求为依据来确定。通过土壤检测的重金属浓度值可以初步判断地块内不同区域内重金属污染程度，根据污染程度的不同对污染地块进行分块修复，地块分块区域的重金属浓度的平均值和最大值，可作为分块修复的依据，同时也为后续筛选修复技术、确定重金属修复药剂使用量等提供支持，而重金属污染区域内重金属的取样并不能完全覆盖到污染区域内每层深度的每一个点，需根据已有的重金属数据预测分块区域内重金属浓度的最大值，重金属污染区域的重金属浓度具有概率分布的特性，因此，可采用数理统计中的极值理论方法评价重金属污染区域内的重金属污染情况。1930年极值理论开始应用到洪水分析、地震分析、降雨量分析、极端气候分析等领域[9]，经过专家学者对极致理论研究的深入，极值理论被应用金融与保险领域中的股票市场崩溃、债券市场瘫痪以及汇率市场危机、工程领域中金属容器的腐蚀情况等[10～14]。1939年瑞典科学家Weibull在材料强度测度中首先用到了极值理论[15]。1958年Gumbel应用极值理论系统解释了洪水统计、气象异常观察值等问题[16]。Fisher[17]提出了极值类型定理，即独立分布的随机变量的最大值通过线性变换后依分布收敛于某一非退化分布。故不论总体分布F(x)是何种形式，其极值分布必定属于极值分布类型中的一种。

1 极值理论及土壤重金属浓度数据统计分析

1.1 极值理论

极值统计用于研究随机变量局部最小值或最大值的分布规律，其原理是对最小值或最大值数据进行极值统计，构造出相关实际问题的数学分析模型，根据数学模型推断最小极值或最大极值的估计值，作为解决实际问题的依据[18]。具体来说就是根据实际工程问题中最主要的检测数据，统计出最小值或最大值数据集合，将其拟合为极值分布类型中的一种，作为实际工程问题的数学分析模型，然后进行统计分析，推断出极小值或极大值的估计值。

表2 极值分布汇总表Tab.2 Extreme value distribution summary table

用广义极值(GEV)分布模型[19]将三参数极值Ⅱ型(Frechet(3P))分布和三参数极值Ⅲ型(Weibull(3P))分布模型统一成一种分布形式，当k>0时，F(x)表示Frechet(3P)分布；当k<0时，F(x)表示Weibull(3P)分布，只计算GEV分布的未知参数即可确定其分布类型，更加便于统计分析。

(1)

1.2 参数估计

各极值分布类型未知参数的常用参数估计方法主要有：矩估计法、概率权值法、线性最小二乘法、极大似然估计法等。

在此采用矩估计法来计算极值I型分布、两参数极值Ⅱ型分布和两参数极值Ⅲ型分布的未知参数，采用概率权值法计算广义极值分布的未知参数。

1.2.1 矩估计

假定Xi(i=1,2,3…)是一个完全样本，由矩估计可以得到极值I型分布、两参数极值Ⅱ型分布(Frechet(2P))和两参数极值Ⅲ型分布的等式。极值I型分布(Weibull(2P))的期望和均方差分别为：

(2)

(3)

根据给定数据，采用传统的期望和均方差公式进行计算，再由式(2)和式(3)计算出极值I型分布未知参数μ和σ。

两参数极值Ⅱ型分布的计算等式为：

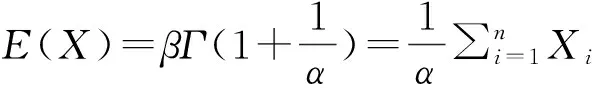
(4)

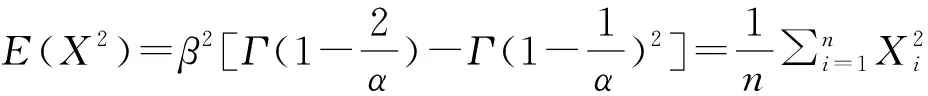
(5)

两参数极值Ⅲ型分布的计算等式为：

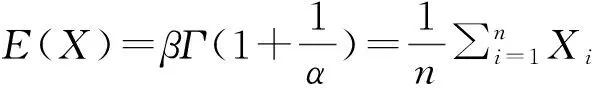
(6)

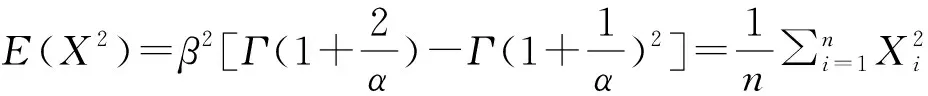
(7)

同理，根据式(4)和式(5)可以计算出两参数极值Ⅱ型分布的未知参数β和α，根据式(6)和式(7)可以计算出两参数极值Ⅲ型分布分布的未知参数β和α。

1.2.2 概率权值法

概率权值法应用简单，且在参数估计中具有较好的计算效果。应用概率权值法可计算广义极值分布的未知参数，具体的计算方法史道济[19]在《实用极值统计方法》中有详细描述。

1.3 土壤重金属浓度数据统计分析

1.3.1 实例分析

某重金属砷污染地块面积为125 478.2m2，在该地块的场地调查过程中发现，地块大部分区域内存在不同程度的重金属砷污染。对该重金属砷污染地块进行详细调查，测定污染区域内的重金属砷浓度，重金属浓度数据较多，为了简化数据模型，选择重金属污染比较严重的3块区域(A区、B区和C区)，将每块区域分成12块，并分别在0.5m、1.5 m和3.0 m深度处取重金属砷浓度的最大值(部分检测点位重金属砷未检出)，最终A、B、C块区域内得到重金属砷浓度数据34个(如表3所示)。

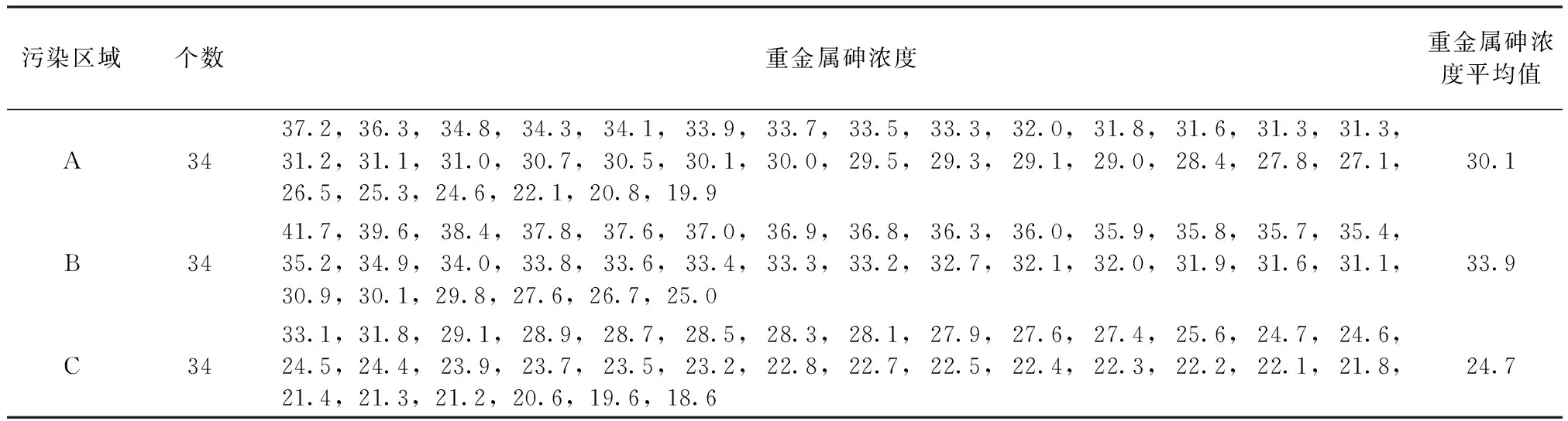
表3 重金属砷浓度数据表

将地块n个重金属砷浓度数据按照从大到小的顺序排列，其中第i个重金属砷浓度数据对应的累计概率为：

重金属砷浓度的经验分布图的X轴为重金属砷浓度数据xi，Y轴为重金属砷浓度数据对应的累计概率yi。

根据上述重金属砷浓度数据，采用矩估计法计算得到Gumbel、Frechet(2P)和Weibull(2P)分布的α和β的值，采用概率权值法计算得到GEV分布的k、σ和μ的值(表4)。

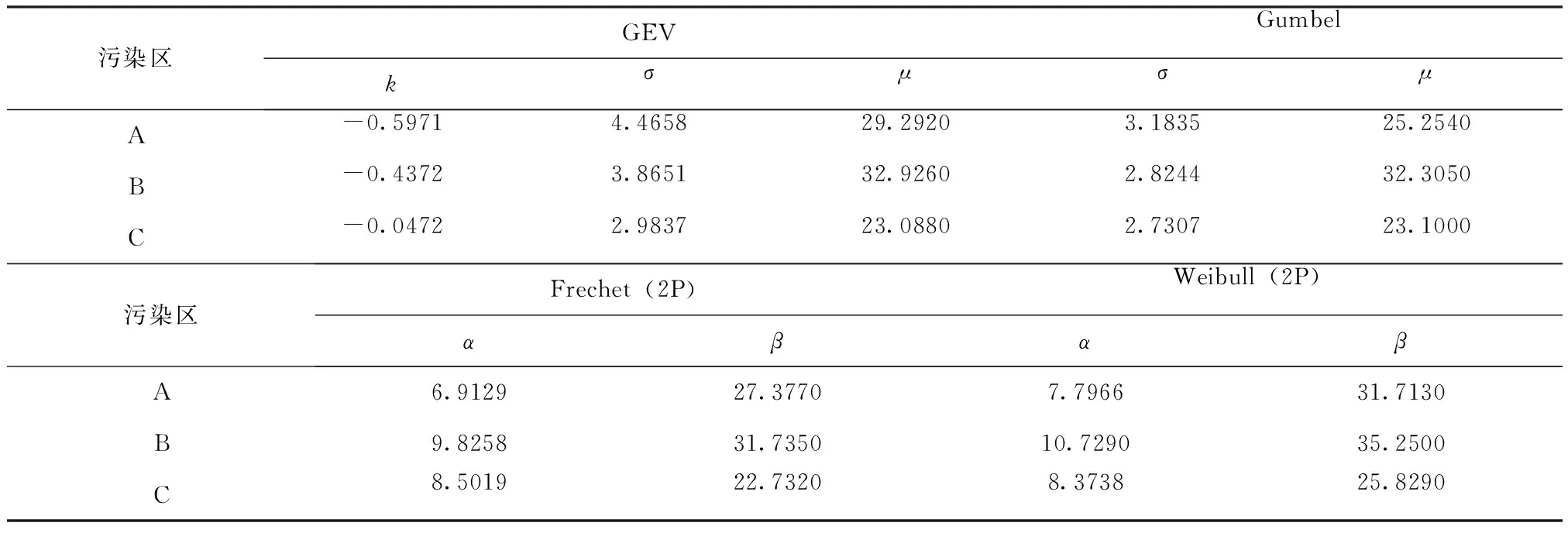
表4 GEV、Gumbel、Frechet(2P)和Weibull(2P)分布的参数估计值

1.3.2 拟合优度检验

拟合优度检验是用于检验某种分布刻画给定数据是否合适的方法[20]。常用方法为：作图法、A-D检验、回归方法、K-S检验法、Χ2检验等。其中，K-S检验法基于累积分布函数，用以检验一个经验分布与某种理论分布或者两种经验分布是否有显著性差异。其原假设H：两个数据分布一致或者数据符合理论分布。D=max|f(x)-g(x)|，当实际观测值D>D(n,α)，则拒绝H假设，否则则接受H假设，通过查表可以得到D(n,α)的值。作图法可形象直观地比较出经验分布与各极值分布的拟合效果，从而比较出与经验分布的拟合效果最好的极值分布形式。P-P散点图可以检验数据是否符合指定的分布，当数据符合指定分布时，P-P图中各点近分布在直线两侧，与直线偏离程度越小，说明拟合效果越好。

根据对A、B、C区域重金属砷浓度的参数估计可知，参数k<0，A、B、C区域重金属砷浓度数据的GEV分布就是Weibull(3P)分布。根据对A、B、C区域数据的4种分布形式进行K-S检验的结果(表5)说明，3个污染区域重金属砷浓度数据的经验分布均拒绝原假设，即重金属砷浓度数据的经验分布均符合各极值分布类型。依据图1～图3可以判断，广义极值分布与3个污染区域重金属砷浓度数据的经验分布的拟合效果最好。

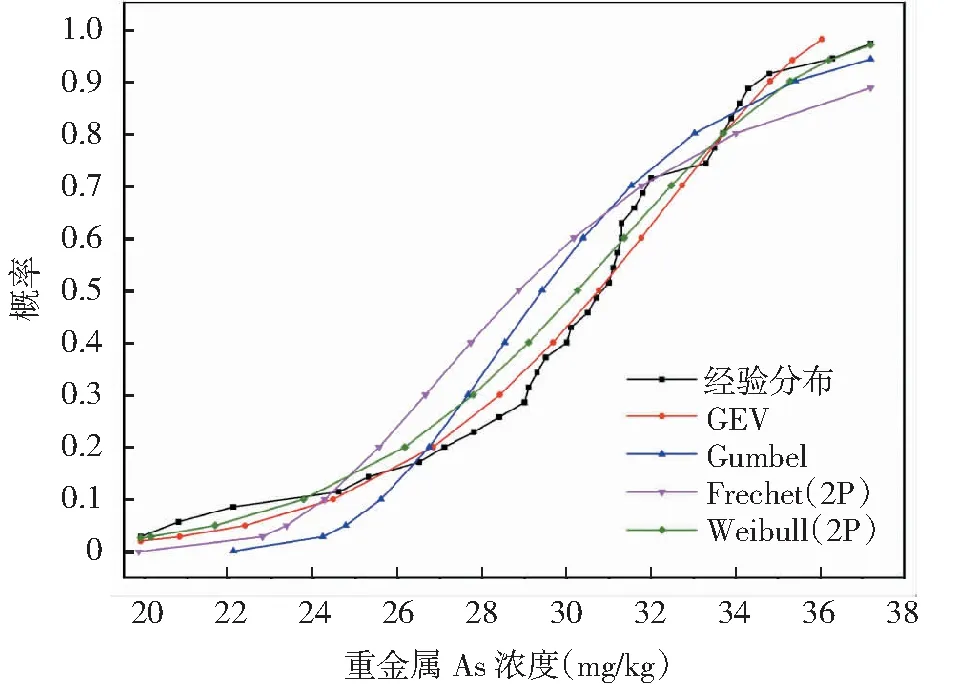
图1 GEV、Gumbel、Frechet(2P)、Weibull(2P)分布与经验分布对比图(A区)Fig.1 Comparison of GEV, Gumbel, Frechet (2P), Weibull (2P) distribution and empirical distribution (region A)

图2 GEV、Gumbel、Frechet(2P)、Weibull(2P)分布与经验分布对比图(B区)Fig.2 Comparison of GEV, Gumbel, Frechet (2P), Weibull (2P) distribution and empirical distribution (region B)

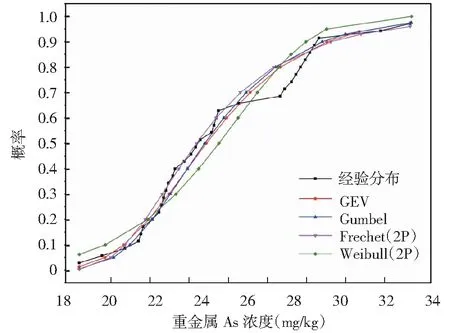
图3 GEV、Gumbel、Frechet(2P)、Weibull(2P)分布与经验分布对比图(C区)Fig.3 Comparison of GEV, Gumbel, Frechet (2P), Weibull (2P) distribution and empirical distribution (region C)

根据图1～图3，广义极值分布与重金属砷浓度数据的经验分布拟合效果最好。GEV分布形式中k参数的取值可以说明：A、B、C区重金属砷浓度数据均服从Weibull(3P)分布。

由A、B、C区重金属砷浓度数据的P-P散点图(图4～图6)可知，A、B、C区重金属砷浓度数据经验分布与广义极值分布的P-P点均分布在直角坐标系中直线y=x的两侧，其余类型的极

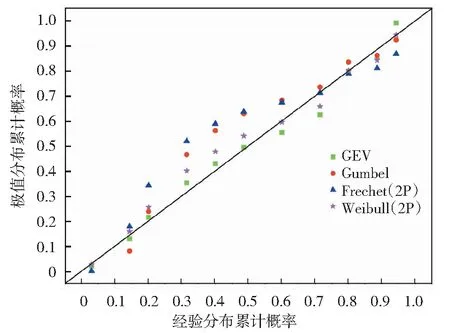
图4 各极值分布累计概率与经验分布概率P-P散点图(A区)Fig.4 The P-P scatter plot for the cumulative probability of each extremum distribution and the probability of the empirical distribution (region A)

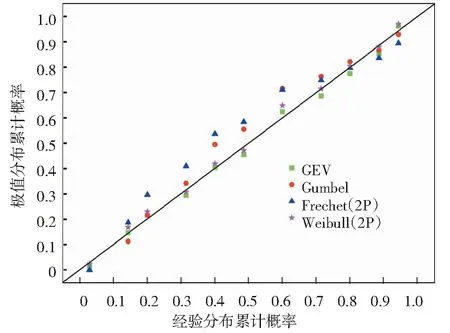
图5 各极值分布累计概率与经验分布概率P-P散点图(B区)Fig.5 The P-P scatter plot for the cumulative probability of each extremum distribution and the probability of the empirical distribution (region B)

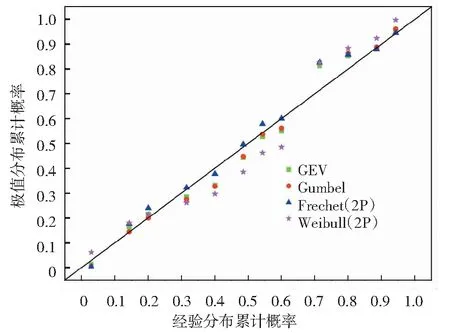
图6 各极值分布累计概率与经验分布概率P-P散点图(C区)Fig.6 The P-P scatter plot for the cumulative probability of each extremum distribution and the probability of the empirical distribution (region C)

值分布与经验分布的P-P点相对于广义极值分布来说偏离直线y=x的程度较大，再次验证广义极值分布与经验分布的拟合效果最好。

1.3.3 重金属砷浓度极值预测

与A、B和C区重金属砷浓度的经验分布拟合效果最优的广义极值分布表达式如式(8)、(9)和(10)：

F(x) =exp[-(-0.1337x+4.9165)1.6748]

(8)

F(x) =exp[-(-0.1131x+4.7244)2.2873]

(9)

F(x) =exp[-(-0.01585x+1.3659)21.1506]

(10)

由此可以根据GEV分布形式预测不同概率下重金属砷浓度最大值，A、B和C区重金属砷浓度数据在不同概率下的重金属砷浓度最大值如表6所示。

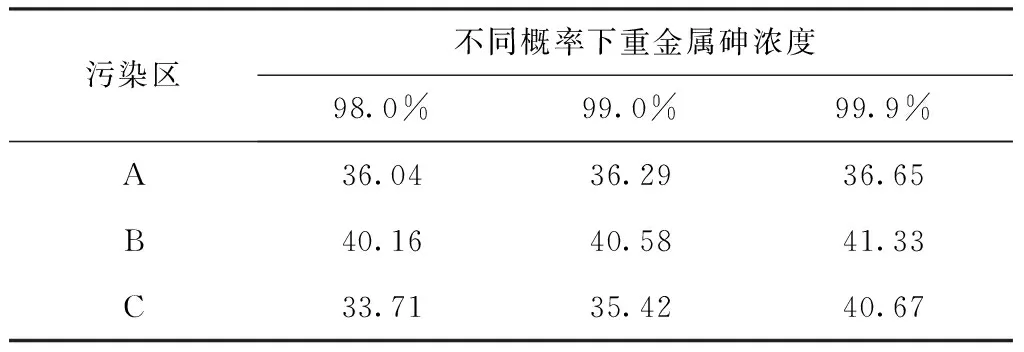
表6 不同概率下的重金属砷浓度最大值Tab.6 The maximum concentration value of heavy metal arsenic under different probabilities (mg/kg)

2 结 论

2.1 极值分布理论的广义极值分布(GEV)模型可以很好地表达Frechet(3P)和Weibull(3P)分布，且对重金属砷浓度数据的拟合效果最好。

2.2 Gumbel分布、Frechet(2P)分布和Weibull(2P)分布的未知参数采用矩估计法计算得出，广义极值分布的未知参数采用概率权值法计算得出。

2.3 K-S检验法可以判断重金属砷浓度数据的经验分布均符合各极值分布类型，作图法可以形象直观的判断出广义极值分布类型与经验分布的拟合效果最好，P-P散点图法再次验证重金属砷浓度数据的经验分布与广义极值分布模型的拟合效果最好。

2.4 通过已有的重金属砷浓度数据可以计算出广义极值分布形式的表达式，由此可以得出污染地块内不同区域重金属砷浓度在不同概率下的最大值。