形如(a2n+1)的孤立数
2021-04-29华程
华 程
(泰州学院 数理学院,江苏 泰州 225300)
0 引言及主要结论
对于正整数n, 设σ(n)是n的所有不同的正因数之和。 如果两个正整数a和b满足
σ(a)=σ(b)=a+b,
(1)
则称(a,b)是一对亲和数。一个相反的问题是:如果对于给定的a,不存在任何正整数b适合(1)式,则称a是一个孤立数(anti-sociable number)。笔者猜测:任何奇数都是孤立数。
本文给出了如下结论。
定理1对任意正整数n,当13≤a≤31,2a时,E(a,n)都是孤立数。
1 关键性引理
引理1素数都是孤立数。
证明设p是素数。 如果p不是孤立数,则有正整数b可使
σ(p)=σ(b)=p+b。
由于σ(p)=p+1,可知b=1。 而σ(1)=1≠p+1,矛盾,故p是孤立数。
引理2对任意正整数m,有σ(m)φ(m)≤m2。
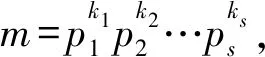

引理3[5]设x,y是互素的正整数,若素数p满足p∣(x2n+y2n),则p=2或p≡1(mod 2n+1)。

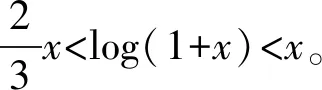
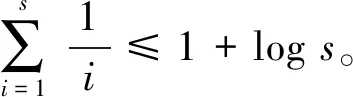
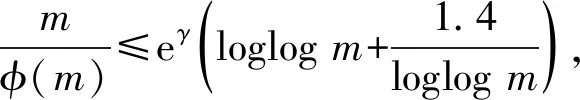
eγ=1.781 072 417 990 198。
2 定理1的证明
由于E(5,n)是孤立数,故E(25,n)都是孤立数。
假定E(a,n)(13≤a≤31,2a,a≠25)不是孤立数,则存在正整数m满足(1),即有
σ(E(a,n))=σ(m)=E(a,n)+m。
(2)
先证明n=1,2,3,4时,E(a,n)都是孤立数。
1)a=13时,由E(13,2)=14 281,E(13,3)=407 865 361为素数及引理1知,E(13,2),E(13,3)是孤立数; 由E(13,1)=5·17知,σ(E(13,1))=108,m=23,σ(m)=24,σ(E(13,1))≠σ(m),故E(13,1)是孤立数;由E(13,4)=2 657·441 281·283 763 713知,σ(E(13,4))=332 834 279 543 502 984,m=11·307·373·100 010 203,σ(m)=138 244 505 030 016,σ(E(13,4))≠σ(m),故E(13,4)是孤立数。
2)a=15时,由E(15,1)=113为素数及引理1知,E(15,1)是孤立数; 由E(15,2)=17·1 489知,σ(E(15,2))=26 820,m=11·137,σ(m)=1 656,σ(E(15,2))≠σ(m),故E(15,2)是孤立数;由E(15,3)=7 121·179 953知,σ(E(15,3))=1 281 632 388,m=52·7·1 069,σ(m)=265 360,σ(E(15,3))≠σ(m),故E(15,3)是孤立数;由E(15,4)=257·12 779 004 583 099 009知,σ(E(15,4))=3 296 983 182 439 544 580,m=2 927·38 737·112 706 333,σ(m)=12 783 700 605 888 576,σ(E(15,4))≠σ(m),故E(15,4)是孤立数。
3)a=17时,由E(17,2)=41 761为素数及引理1知,E(17,2)是孤立数; 由E(17,1)=5·29知,σ(E(17,1))=180,m=5·7,σ(m)=48,σ(E(17,1))≠σ(m),故E(17,1)是孤立数;由E(17,3)=18 913·184 417知,σ(E(17,3))=3 488 082 052,m=3·67 777,σ(m)=271 112,σ(E(17,3))≠σ(m),故E(17,3)是孤立数;由E(17,4)=257·1 801 601·52 548 582 913知,σ(E(17,4))=24 425 281 075 357 282 824,m=7 307·148 303·87 376 123,σ(m)=94 698 735 293 530 368,σ(E(17,4))≠σ(m),故E(17,4)是孤立数。
4)a=19时,由E(19,1)=181为素数及引理1知,E(19,1)是孤立数; 由E(19,2)=17·3 833知,σ(E(19,2))=69 012,m=3 851,σ(m)=3 852,σ(E(19,2))≠σ(m),故E(19,2)是孤立数;由E(19,3)=15 073·563 377知,σ(E(19,3))=8 492 359 972,m=3·192 817,σ(m)=771 272,σ(E(19,3))≠σ(m),故E(19,3)是孤立数;由E(19,4)=97·1 486 811 410 142 377 153知,σ(E(19,4))=145 707 518 193 952 961 092,m=3·25 583·19 372 388 045 999,σ(m)=1 982 492 703 075 456 000,σ(E(19,4))≠σ(m),故E(19,4)是孤立数。
5)a=21时,由E(21,2)=97 241为素数及引理1知,E(21,2)是孤立数; 由E(21,1)=13·17知,σ(E(21,1))=252,m=31,σ(m)=32,σ(E(21,1))≠σ(m),故E(21,1)是孤立数;由E(21,3)=62 897·300 673知,σ(E(21,3))=18 911 793 252,m=13·27 967,σ(m)=391 552,σ(E(21,3))≠σ(m),故E(21,3)是孤立数;由E(21,4)=1 217·2 689·31 873·6 857 635 489知,σ(E(21,4))=716 160 780 055 575 229 200,m=112·73·2 230 219·44 490 157,σ(m)=976 551 192 999 987 920,σ(E(21,4))≠σ(m),故E(21,4)是孤立数。
6)a=23时,由E(23,2)=139 921为素数及引理1知,E(23,2)是孤立数; 由E(23,1)=5·53知,σ(E(23,1))=324,m=59,σ(m)=60,σ(E(23,1))≠σ(m),故E(23,1)是孤立数;由E(23,3)=17·3 697·623 009知,σ(E(23,3))=41 470 037 640,m=13·178 041 923,σ(m)=2 492 586 936,σ(E(23,3))≠σ(m),故E(23,3)是孤立数;由E(23,4)=193·15 887 591 750 468 908 417知,σ(E(23,4))=3 082 192 799 590 968 233 092,m=32·1 625 153·1 086 228 787 243,σ(m)=22 948 757 760 561 562 488,σ(E(23,4))≠σ(m),故E(23,4)是孤立数。
7)a=27时,由E(27,1)=5·73知,σ(E(27,1))=444,m=79,σ(m)=80,σ(E(27,1))≠σ(m),故E(27,1)是孤立数;由E(27,2)=41·6 481知,σ(E(27,2))=272 244,m=11·593,σ(m)=7 128,σ(E(27,2))≠σ(m),故E(27,2)是孤立数;由E(27,3)=17·97·193·577·769知,σ(E(27,3))=152 306 652 960,m=17·97·6 726 431,σ(m)=11 865 426 048,σ(E(27,3))≠σ(m),故E(27,3)是孤立数;由E(27,4)=76 801·21 523 361·24 127 552 321知,σ(E(27,4))=39 883 742 699 152 216 808 328,m=52 189·9 986 026 096 723,σ(m)=521 170 701 988 025 560,σ(E(27,4))≠σ(m),故E(27,4)是孤立数。
8)a=29时,由E(29,1)=421,E(29,2)=353 641,E(29,4)=125 123 236 840 173 674 393 761为素数及引理1知,E(29,1),E(29,2),E(29,4)是孤立数;由E(29,3)=17·26 209·561 377知,σ(E(29,3))=264 846 912 840,m=7 583·1 941 673,σ(m)=14 725 655 616,σ(E(29,3))≠σ(m),故E(29,3)是孤立数。
9)a=31时,由E(31,1)=13·37知,σ(E(31,1))=532,m=3·17,σ(m)=72,σ(E(31,1))≠σ(m),故E(31,1)是孤立数;由E(31,2)=409·1 129知,σ(E(31,2))=463 300,m=34·19,σ(m)=800,σ(E(31,2))≠σ(m),故E(31,2)是孤立数;由E(31,3)=17·25 085 030 513知,σ(E(31,3))=451 530 549 252,m=11·59·38 651 819,σ(m)=27 829 310 400,σ(E(31,3))≠σ(m),故E(31,3)是孤立数;由E(31,4)=1 889·1 347 329·6 139 297·23 277 313知,σ(E(31,4))=363 904 447 727 903 776 016 400,m=192 886 854 311 144 102 159,σ(m)=192 886 854 311 144 102 160,σ(E(31,4))≠σ(m),故E(31,4)是孤立数。
综上,当n=1,2,3,4时,E(a,n)都是孤立数。
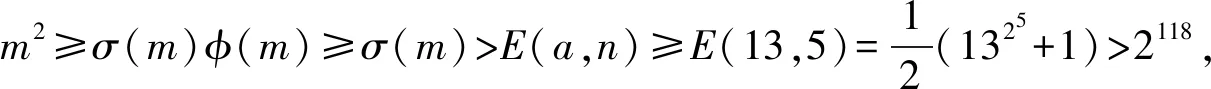
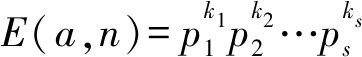
E(a,n)≥p1p2…ps>(2n+1+1)s。
(3)
由于n≥5,故由(3)式及引理4可得
(4)
再由(2)式及引理2、引理5,可得
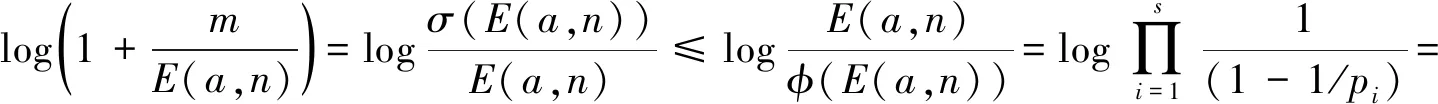
(5)
又pi≡1(mod 2n+1),pi≥2n+1i+1,i=1,2,…,s,代入(5)式,根据引理6,并结合(4)式,有
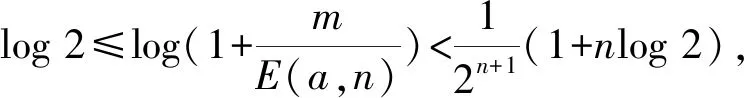
(6)
由于254>e40,所以log logm>log 40>3.6,根据引理2、引理7,得
(7)
由(6)式、(7)式可得
2n+2<3(1+nlog 2)(1.79log logm+0.7)。
(8)

(9)
结合(8)(9)两式得
2n+2<3(1+nlog 2)(1.79log(5·2n-3)+1.79log log 2+0.7)。
(10)
当n≥5时,(10)式不能成立(事实上,n=5时,左边为128,右边为121.92;n>5时,指数比对数增加更快)。因此,E(a,n)在13≤a≤31,2|/a时都是孤立数。定理得证。
