密封弧面半径对C形组合密封圈密封性能的影响
2021-04-29李海宁陈柳青曾佑奎曹春玲
李海宁, 陈柳青, 曾佑奎, 曹春玲
(西安科技大学机械工程学院, 西安 710054)
橡胶密封圈是密封装备的一种通用型基础元件,在密封和泄露这一对冲突中扮演十分必要的角色。密封虽然不属于顶尖的技术,但却也发挥着必不可少的作用。密封圈工作中所用的设备和工作的环境决定了其工作介质,譬如某些船只或在海上的机械大多数密封圈的工作介质都是海水。海水介质特殊的理化特性,造成了更加严峻的损伤、漏液及侵蚀等技术难题,因此,对工作介质为海水的密封元件密封性能的研究意义重大。
随着计算机技术的发展,目前利用有限元仿真技术进行密封圈密封性能的相关研究较多[1-6],肖彬[2]通过Newton-Raphson非线性算法,研究橡胶密封圈在刚性力作用下的应力与变形,通过分析指出橡胶材料在应变过程中产生疲劳和老化的区域,为橡胶材料可靠设计、优化提供了一定的指导意义。钟亮等[7]在建立O形密封圈有限元模型的基础上,分析了预压缩量、流体压力、摩擦系数以及运动速度对O形密封圈密封性能的影响,得到流体压力和摩擦系数是影响O形密封圈密封性能主要因素的结论。李红振等[8]分析了不同流体压力和预压缩率对X形密封圈力学性能的影响,得到X形密封圈在较低的流体压力和预压缩率下发生应力集中。赵敏敏等[9]对O形密封圈的二维轴对称模型在不同径向间隙和不同油压下的密封性能进行了分析,得到径向间隙以及油压对O形密封圈密封性能的影响。以往的有限元仿真技术对密封原件的相关研究中,所研究的密封结构及工作形式都相对简单,如针对O形密封圈[10]或者矩形密封圈的静密封形式的分析。很少有学者对组合密封圈的动密封形式特别是旋转密封形式进行相关研究[11]。
现以海上机械上使用的C形组合密封圈为研究对象,采用有限元仿真软件ANSYS建立其模型,分析密封弧面半径对其密封性能的影响。
1 有限元仿真
C形组合密封圈实物图及结构图如图1所示。
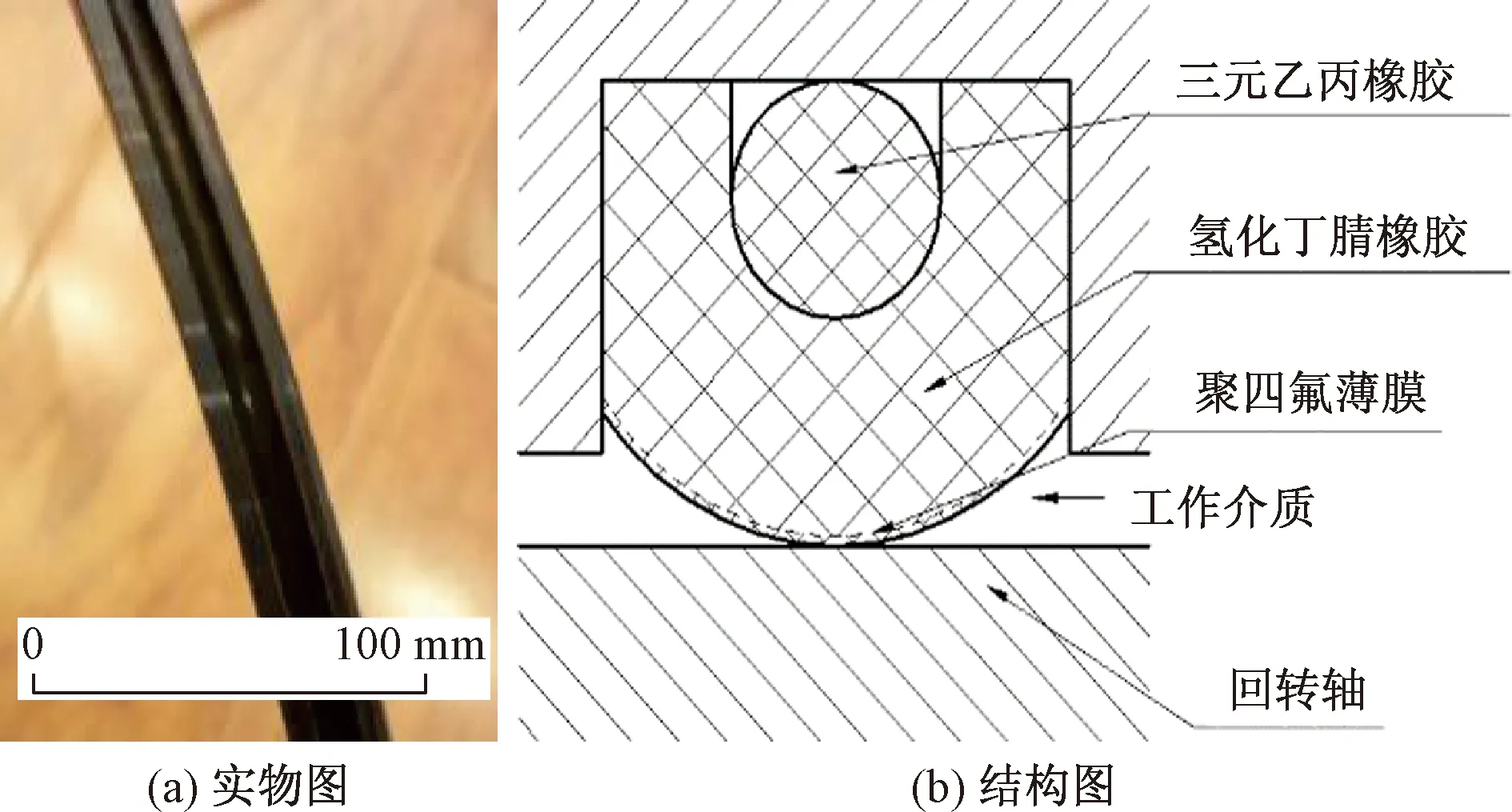
图1 C形组合密封圈实物图及结构图Fig.1 Physical picture and structure diagram of C-type combined sealing ring
弧面半径的变化将会引起C形组合密封圈密封性能的改变,如图2所示为密封弧面半径大小不一的C形组合密封圈。
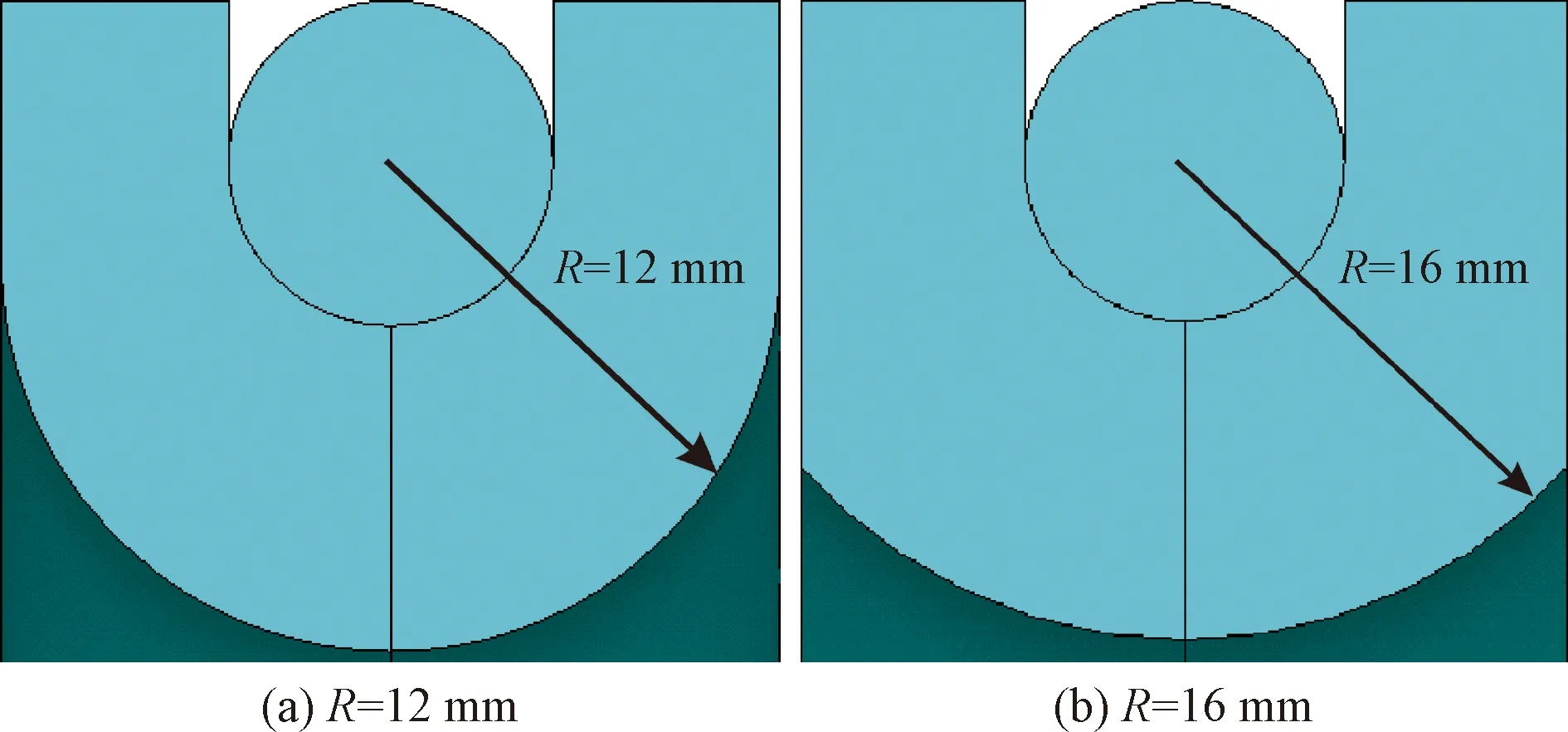
图2 不同弧面半径的密封圈Fig.2 Sealing rings with different arc radius
1.1 有限元分析模型
将某海上设备中回环往复处使用的C形组合密封圈作为探究对象。密封圈安装于沟槽内,凭借C形圈弧面对回转轴的外圆面进行密封。该组合密封圈外部的C形密封环由氢化丁腈橡胶构成,内部的O形密封圈由三元乙丙橡胶制成,且外部的C形密封环密封弧面均匀贴附一层厚度为0.2 mm的聚四氟乙烯薄膜。
由氢化丁腈及三元乙丙材料组成的C形组合密封圈都属于超弹性材料[12],具备高度的非线性,即几何、材料以及接触非线性。在ANSYS软件中用近似不可压缩的Mooney-Rivlin模型来描述这类橡胶材料,应变能方程为
W=C10(I1-3)+C01(I2-3)
(1)
式(1)中:I1、I2为应变张量的两个主不变量;C10、C01为Mooney-Rivlin的材料常数。其中氢化丁腈橡胶C01=18.54,C10=-5.928;三元乙丙橡胶C01=5.046 67,C10=-1.096 7。
在分析中,为了能清晰地展示密封圈内外结构及与端盖之间的装配状态,建立实体模型如图3所示为模型中的1/2。在数值模拟经计算过程中,为缩小计算量,在ANSYS中取密封结构的1/4进行分析,选取单元类型为20节点的SOLID186单元,选六面体扫略划分,把回转轴和沟槽隐藏,有限元模型如图4所示。
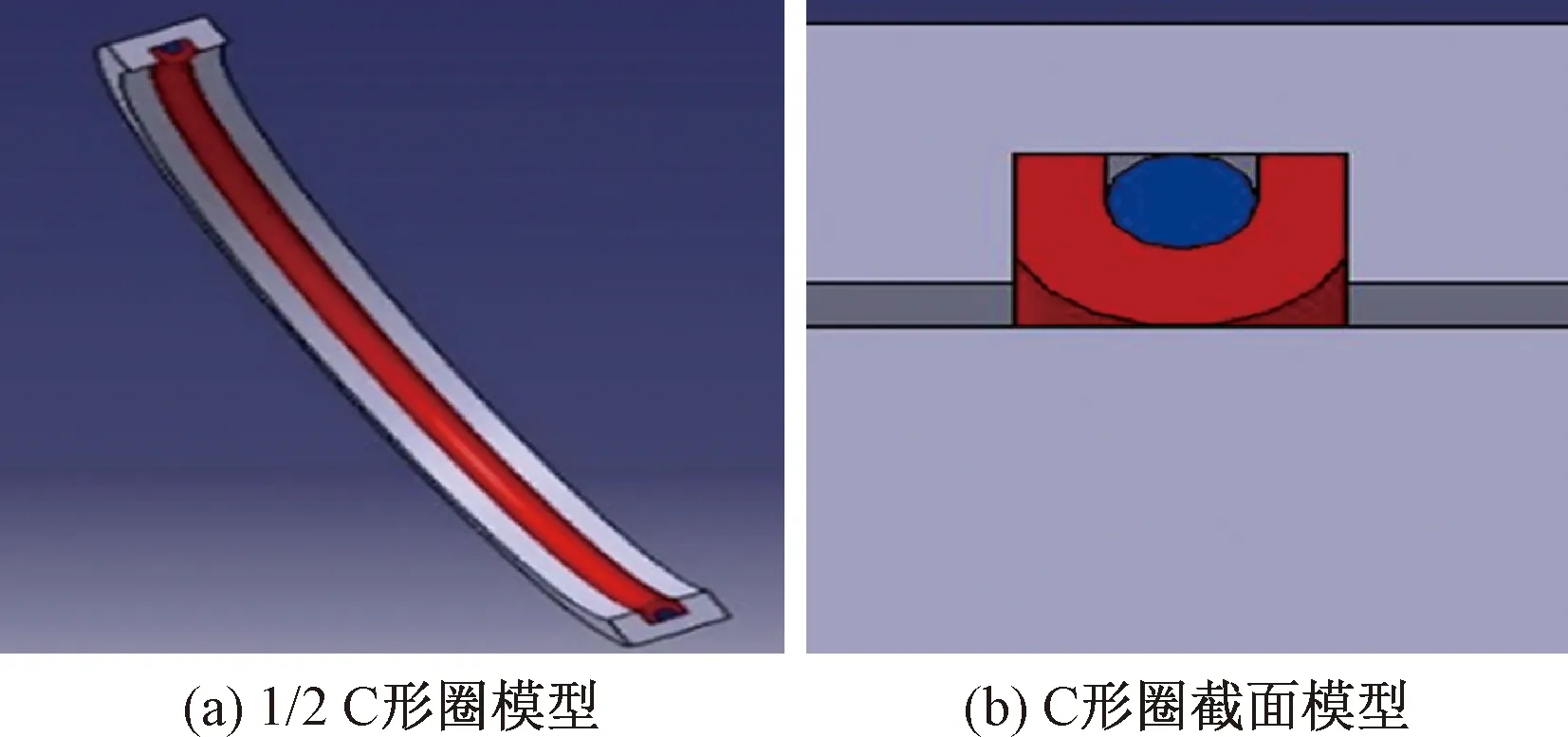
图3 实体模型Fig.3 Solid model

图4 有限元模型Fig.4 Finite element model
1.2 接触问题分析
在此实体模型下,所有零件互相构成面与面的接触,氢化丁腈[13]和三元乙丙橡胶构成柔体与柔体的接触,密封圈与顶部端盖、底部工作轴之间均构成柔体与刚体的接触,具体如图5所示。
整体密封结构中四个接触对如下所述:
(1)三元乙丙橡胶与氢化丁腈橡胶间的接触:即图5中所示面9、8、7和面13、12。
(2)C形圈和端盖沟槽的接触:即图5所示第二个接触对为面11、10、6、5和面3、2、1。
(3)三元乙丙橡胶和沟槽刚体的接触:即面12与面2。
(4)底部C形圈圆弧面以及回转轴外圆表面的接触:即图5所示第四个接触对为面4和面14。
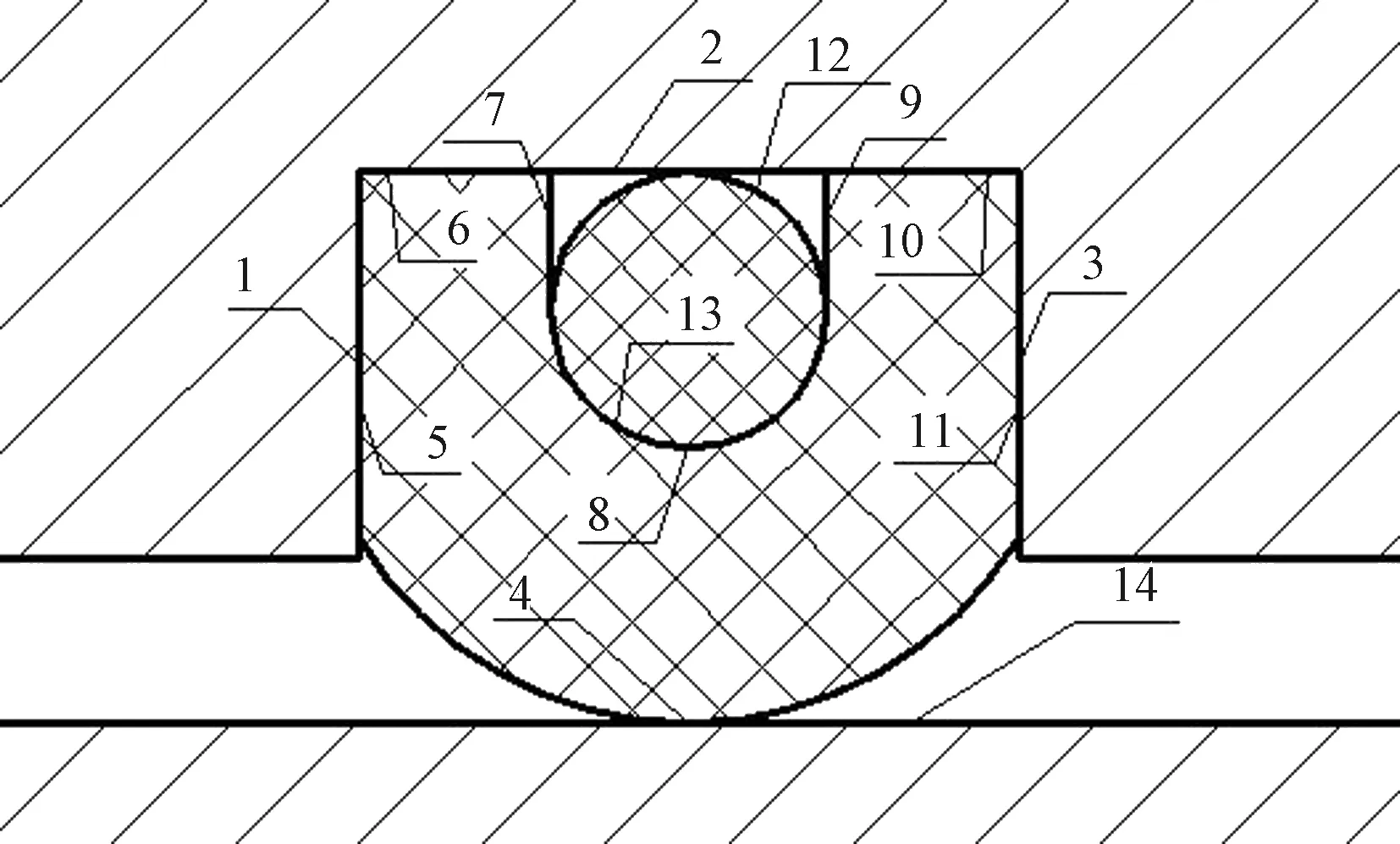
1为端盖沟槽;2为端盖沟槽;3为端盖沟槽;4为U形圈弧面;5为U形圈;6为U形圈;7为U形圈内表面;8为U形圈内表面;9为U形圈内表面;10为U形圈;11为U形圈;12为U形圈内表面;13为O形圈内表面;14为回转轴外圆面
1.3 施加边界条件及载荷
进行前处理之后对模型进行边界条件的定义如下:
(1)仿真时只取模型的1/4来计算,所以要在其实体模型端面上添加一个对称束缚。
(2)依据动静密封的分析条件,对沟槽的全部自由度进行约束。
(3)向密封弧面方向给工作轴外圆面添加一个偏移值,施加效果为密封圈受工作轴的挤压,这时会比较接近装配的状态。
(4)作静密封分析时,给密封弧面半径1/2处添加一定介质压力,并将回转轴全部自由度限制。
(5)作动密封分析时,则在静密封条件基础上,删除工作轴上的所有约束然后把它上面的全部节点转到新的柱坐标系中,首先给全部节点添加一个旋转约束进而将其他5个自由度限制。
2 仿真结果及分析
要探讨控制不同密封弧半径大小可能给密封圈的密封性能[14-15]带来的作用,现取下列参数即密封弧半径12、12.5、13、13.5、14、14.5、15、15.5、16 mm 的密封圈作数值仿真,设定其他分析参数,分别为介质压力6 MPa,O形圈半径5 mm,密封弧摩擦系数0.1,压缩量13%。计算结束后会分别获得对应状态下各个弧面半径Von Mises应力、剪切应力及接触压力云图。
2.1 Von Mises应力
从众数值模拟图中选弧面半径等于12、16 mm时,动密封状态下的密封圈Von Mises应力云图,如图6所示。
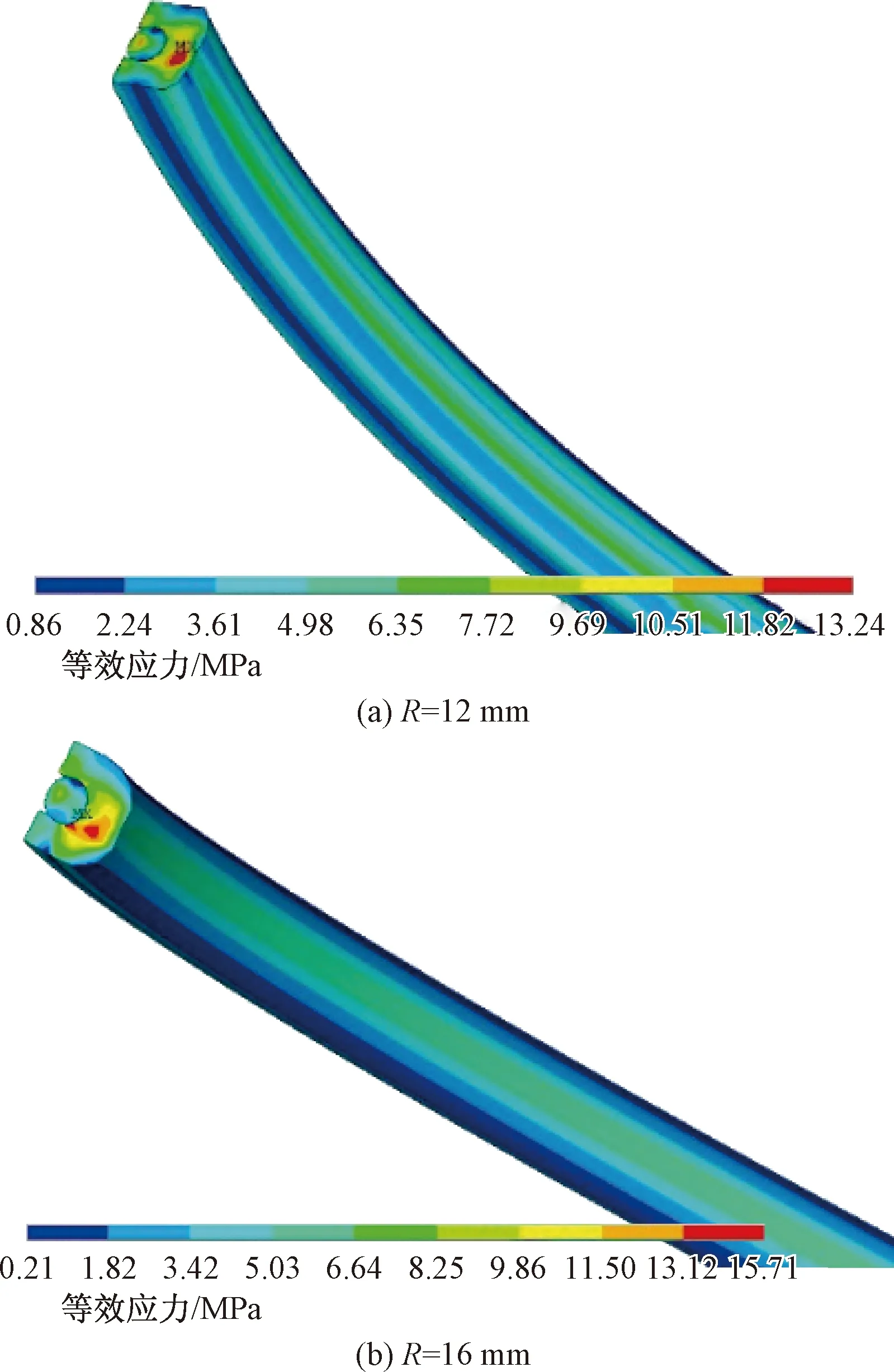
图6 Von Mises应力云图Fig.6 Von Mises stress
表1所示为基于以上条件下整理的动静密封情况下的最大Von Mises应力数据。
将表1中的数据即动静密封状态下密封圈相应的最大Von Mises应力绘成了弧面半径x-最大Von Mises应力yv折线图如图7所示。
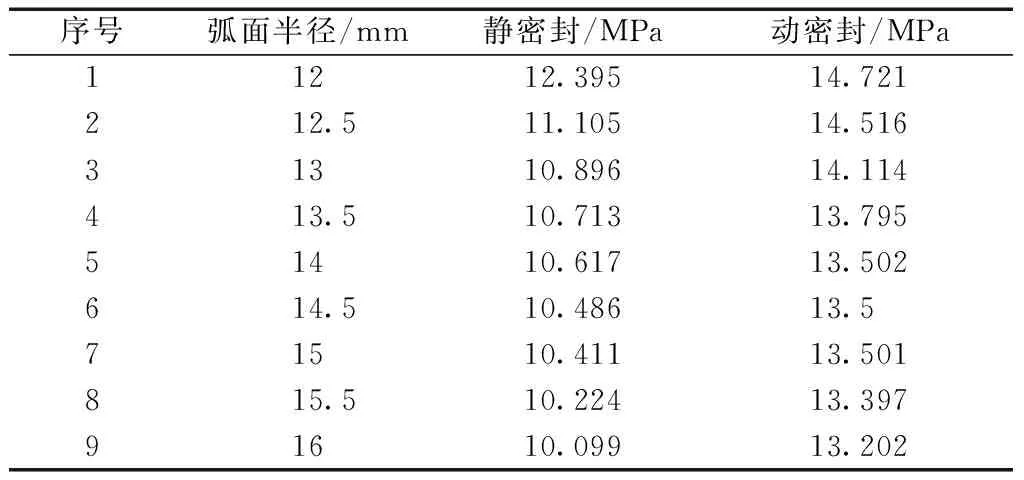
表1 不同弧面半径下最大Von Mises应力
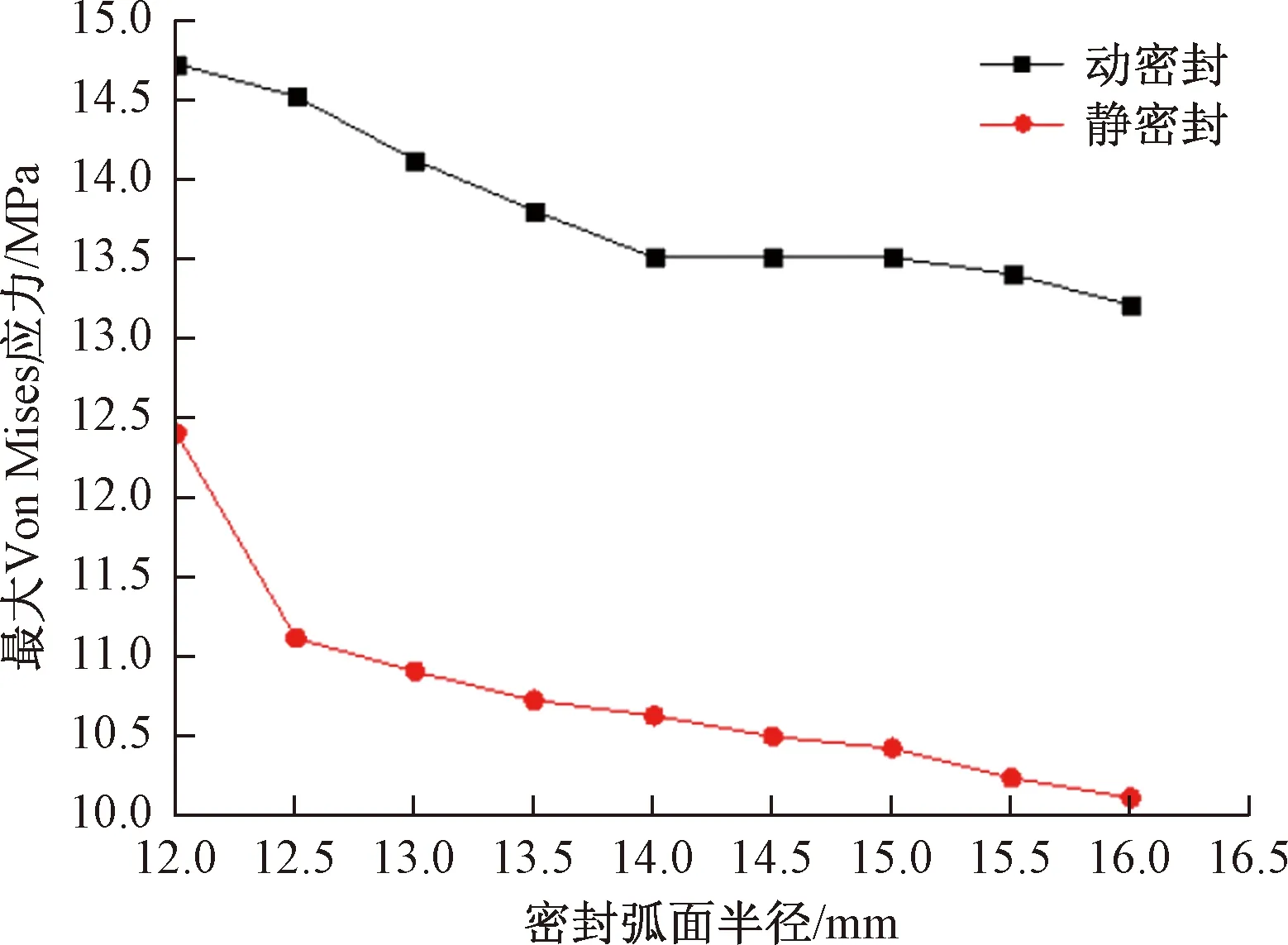
图7 最大Von Mises应力曲线Fig.7 Change curve of maximum Von Mises stress
据图6可得,O形圈和C形圈的接触单元周边以及工作轴和C形圈接触单元周边的Von Mises应力都相应比较小,最大应力发生在C形圈中间,在O形圈与密封弧面位置中部。
据表1中数据以及图7折线图走向结合可以得出,静密封中折线大致走向趋势为:当x增加,yv变小。yv的峰值12.395 MPa出现在x=12 mm的时候,随着x增加至12.5 mm时,yv非常快地减至11.105 MPa,yv在x为12.5~16 mm进一步减小,但减小速率比12~12.5 mm区段要小很多。
动密封中当x=12 ~14 mm时,yv由 14.721 MPa 减小到13.502 MPa。在14~15 mm时yv大致维持稳定不变。当x于15~16 mm区间其最大Von Mises应力又呈现逐渐变小的趋向。由表1及图7可得静密封中的最大Von Mises应力全部小于动密封,这是由于当回转轴工作时会令组合密封圈产生挤压,发生形变,该形变的方向与旋转轴方向相同。动静密封中不同参数条件下最大Von Mises应力都比许用值18.3 MPa小。
因Von Mises应力愈大,材料产生损坏的可能性愈大,故依据上面的分析,密封弧面半径的选取不能太小。
2.2 剪切应力
图8所示为弧面半径R=12 mm及R=16 mm 密封圈在动密封情况下的剪切应力云图。
表2所示是基于以上条件下整理的动静密封情况下的最大剪切应力数据。
将表2中的数据即动静密封状态下密封圈相应的最大剪切应力绘成了折线图,如图9所示。
据图8可得,最大剪切应力出现的位置在以密封圈的对称轴为参照并与此对称轴夹角为45°方向上的对称。由于其方向相反,故正值与负值相对应。
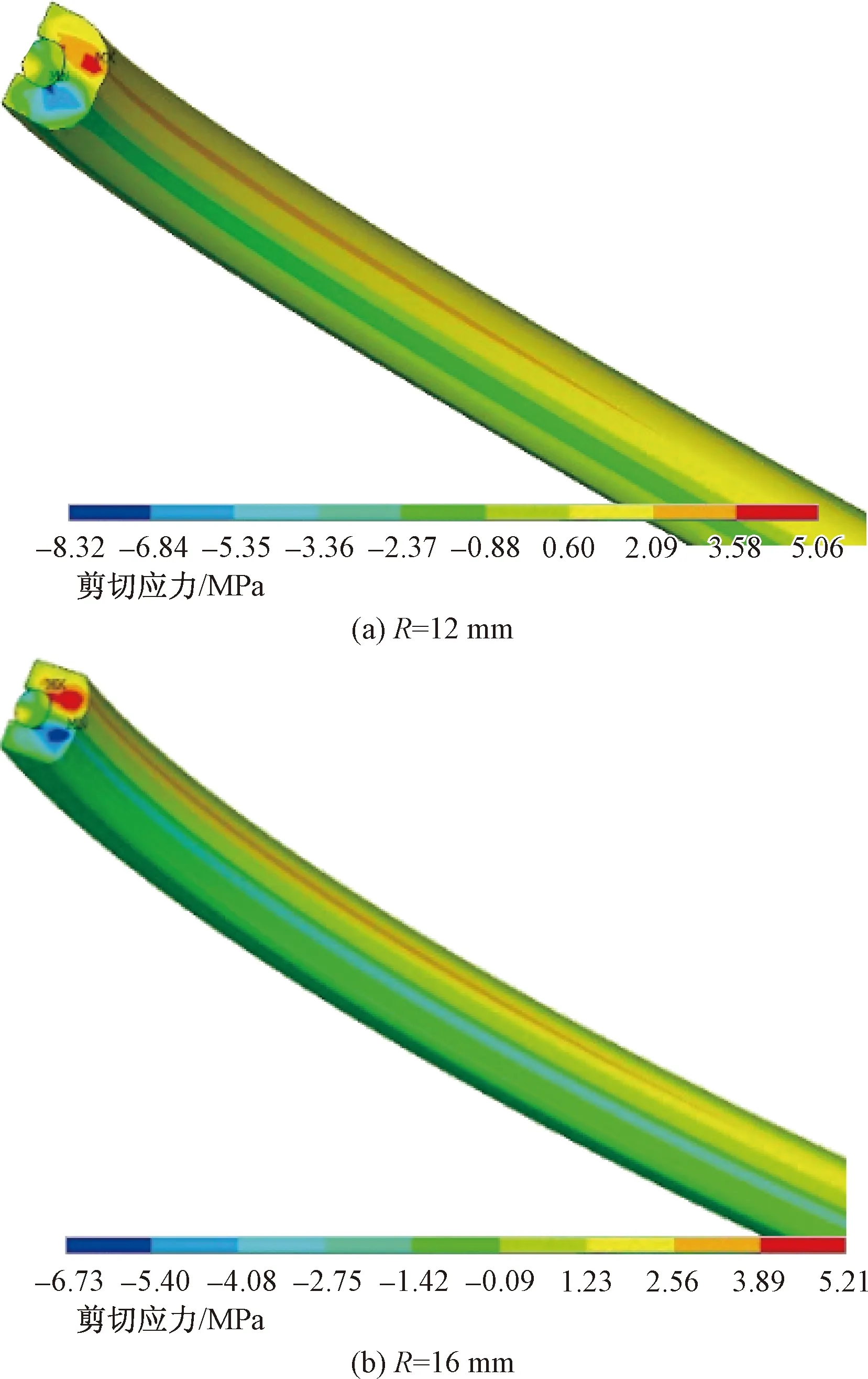
图8 剪切应力云图Fig.8 Shear stress
在此,ys表示最大剪切应力,x同上。结合表2和图9可得,在静密封分析中,其ys起初随x的增加有个小范围的变小,当x>13 mm以后,ys开始逐渐增大为最大值4.12 MPa。
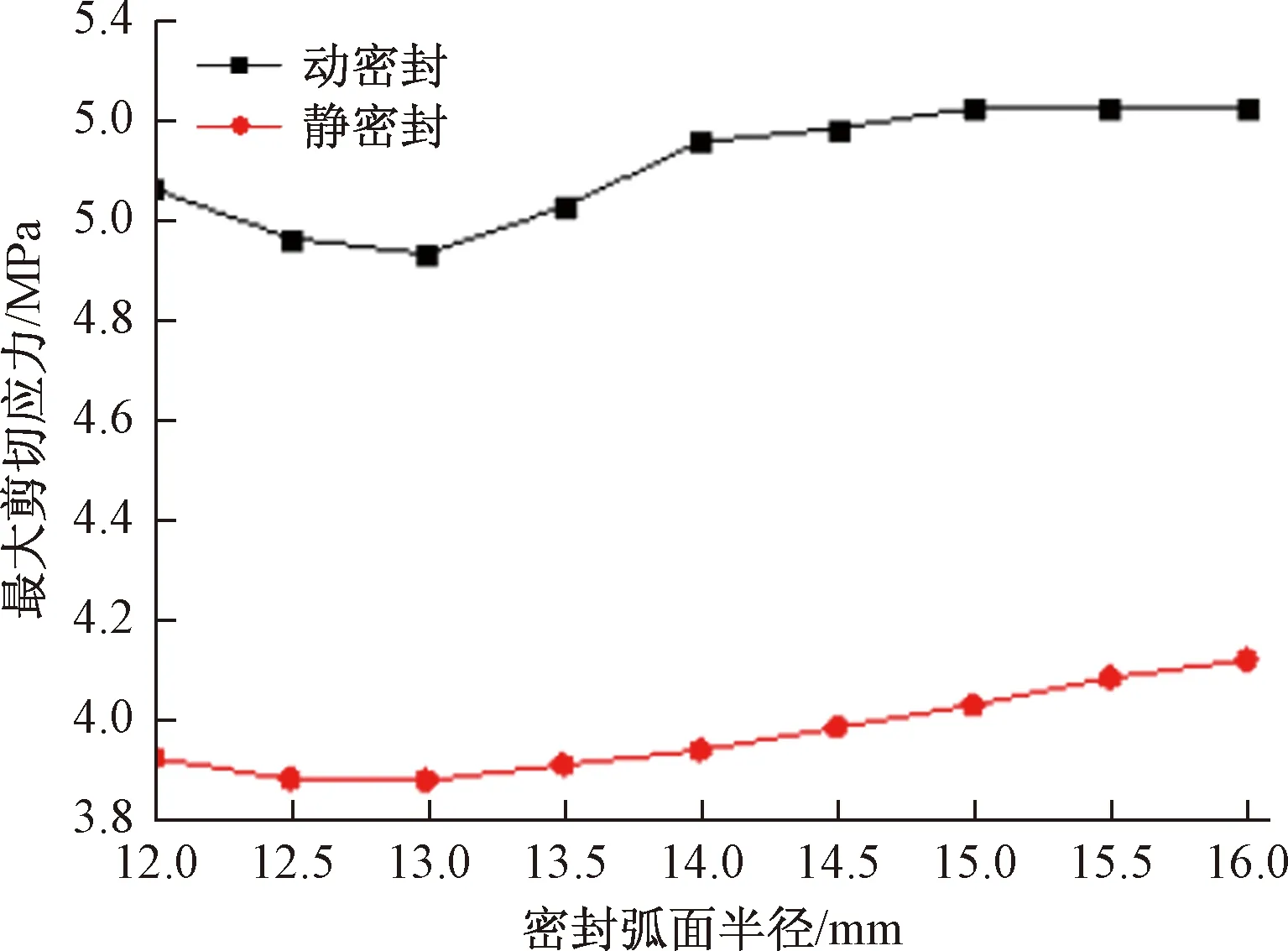
图9 最大剪切应力变化曲线Fig.9 Change curve of maximum shear stress
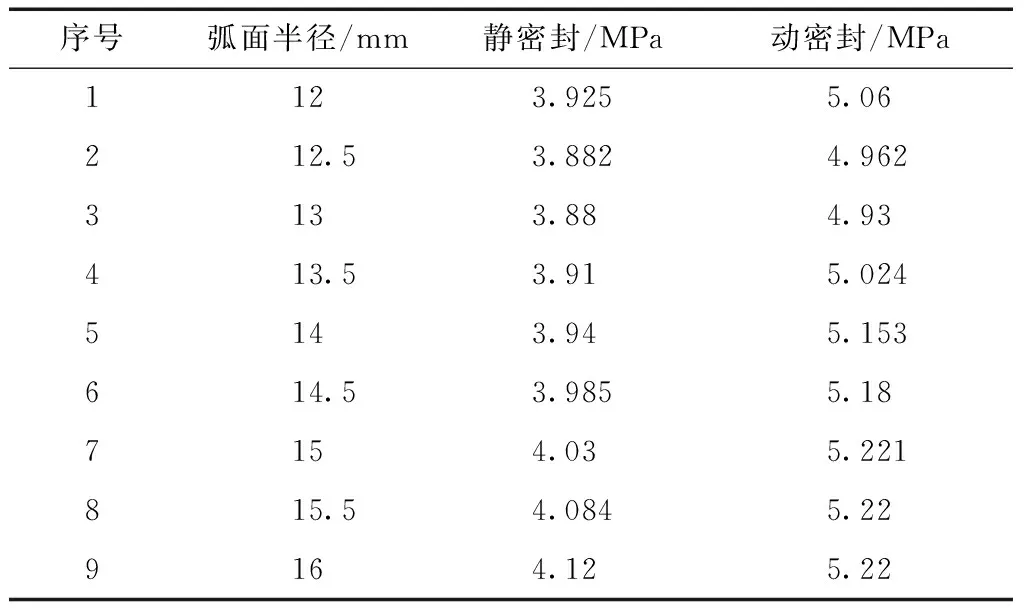
表2 不同弧面半径下最大剪切应力
在动密封情况中,最大剪切应力起初同样也有一个小范围的变小,在x>13 mm以后开始逐渐增大,但增加的速率在x=14~16 mm时要小于13~14 mm。x=16 mm时,其ys为5.22 MPa,比氢化丁腈橡胶许用值8.6 MPa要小,故该组合密封圈可以正常工作,保证其密封效果。同上,在各参数组合下工作轴旋转引起的密封圈形变使静密封下的最大剪切应力值均小于动密封状态下的值。
因剪切应力愈大,材料愈容易产生剪切破坏,故必须把握剪切应力的大小。
2.3 接触压力
图10所示为弧面半径R=12 mm及R=16 mm 时,密封圈在动密封状态下的接触压力云图。
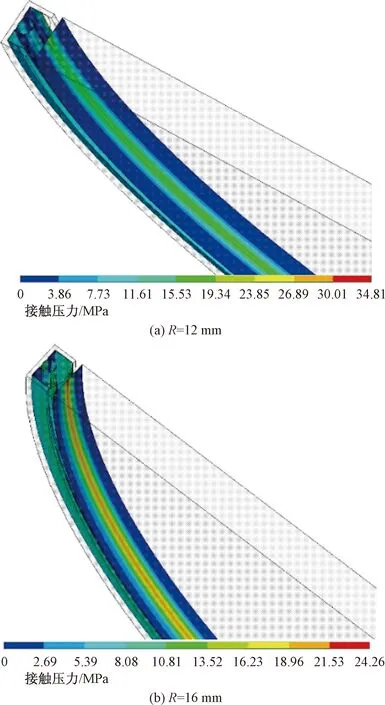
图10 接触压力云图Fig.10 Contact pressure
表3所示是基于以上条件下整理的动静密封情况下的最大接触压力数据。
将表3中的数据即动静密封状态下密封圈相应的最大接触压力绘成了弧面半径x-最大接触压力yc折线图,如图11所示。
在动密封情况中,最大接触压力在密封弧面半径为12~13 mm内有个迅速减小的趋势,由 34.82 MPa 减到24.3 MPa,之后在24.3 MPa附近趋于稳定。由表3及图11可以发现,在x最小的时候yc最大,这是在x最小时,压力散步较为密集,密封圈与回转轴之间的触及面积最小。
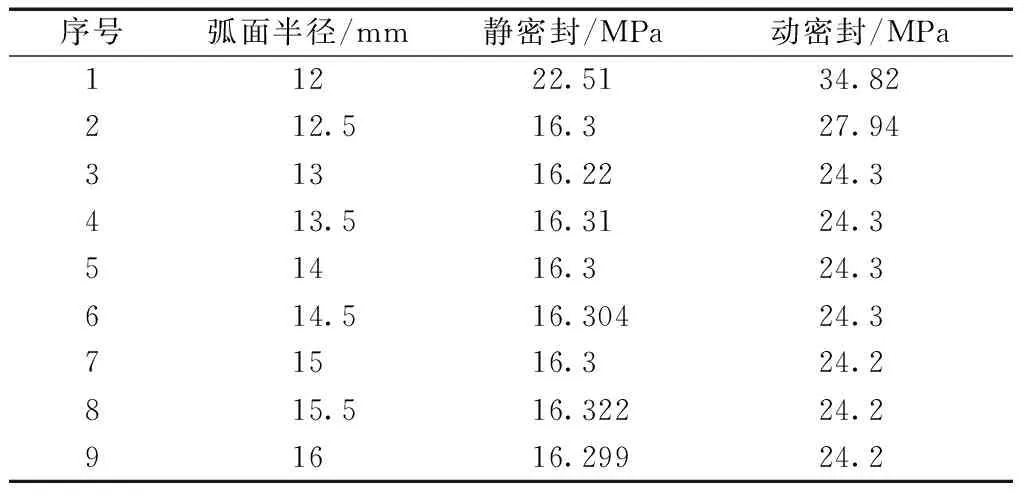
表3 不同弧面半径下最大接触压力
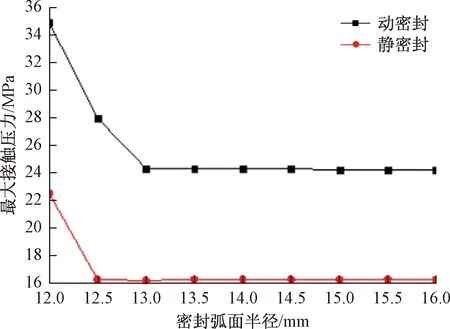
图11 最大接触压力变化曲线Fig.11 Change curve of maximum contact pressure
尽管密封副处的接触压力值会确定密封圈不失效时最大介质压力,然而在此C形组合密封圈的工作介质压力不超过6 MPa,太大的接触压力不仅不可以提升密封性能,还能增大密封弧面磨损速度,使得密封圈使用寿命减小。
3 结论
(1)在不同弧面半径的参数下,密封圈都可以达到密封效果。
(2)在弧面半径较大时,由于Von Mises应力以及剪切应力都较大,增加了密封失效可能性。
(3)在弧面半径较小时,密封副处接触压力比较大,增大了密封圈的磨损率,减短其使用寿命。
(4)当密封弧面半径选择13 mm时,最大Von Mises应力和剪切应力比较小,密封副处的接触压力适中,此值较为合理。
