基于涡流发生器的翼型风洞试验侧壁干扰控制研究
2021-04-29魏斌斌高永卫师尧李栋郝礼书
魏斌斌,高永卫,师尧,李栋,郝礼书
(西北工业大学航空学院,西安710072)
0 引言
翼型的气动特性直接决定了飞机机翼、风力机、螺旋桨、直升机旋翼等的气动性能,因此,获得准确、可靠的翼型气动性能数据是必须的。目前,可靠的翼型气动性能通常通过风洞试验的方法获取,翼型风洞试验数据的准确性取决于洞壁干扰效应的大小,而计算流体力学(Computational Flu⁃id Dynamics,简称CFD)技术的迅速发展给风洞试验提出了更严格的准度要求,因此需要对洞壁干扰效应进行更加细致的研究。
翼型风洞试验存在两类最主要的干扰效应:上下壁干扰效应和侧壁干扰效应。上下壁干扰效应是一个二维的、无黏的问题,其修正方法已发展得相对成熟[1-2]。而侧壁干扰效应是一个有黏的、三维流动问题[3-5],目前减弱侧壁干扰的有效方式是对其进行流动控制。
在翼型风洞试验中,为了实现大雷诺数,会使用弦长相对较大的模型。弦长大意味着展弦比小,展弦比较小时,侧壁边界层的发展会显著影响翼型气动特性。对于小展弦比翼型,其诱导出的逆压梯度与侧壁边界层相互干扰,引起侧壁边界层分离。侧壁边界层一旦分离,会在翼型模型与侧壁之间形成角区流动,这种角区流动呈现三维特征[6-8]。横向流动由侧壁向翼型中线逐渐发展,由于对称性,理论上翼型中线横向流速为零。这种三维效应使翼型中线环量减小,升力减小[9-10]。N.Sudani等[5]的研究表明,为了减小侧壁干扰效应的影响,低马赫数试验情况下,翼型模型的展弦比至少要达到1.5,高马赫数情况下,至少要达到2.0。
为了消除或减弱这种角区分离流动带来的三维效应,需使用边界层控制(Boundary-layer Con⁃trol,简称BLC)技术。目前,吹气[9]和吸气[4,11]是最常用的侧壁边界层控制方法。吹气为风洞壁上的边界层提供能量,使其能够抵抗翼型模型诱导出的逆压梯度引起的流动分离。抽吸气去除了侧壁边界层,减小了侧壁边界层厚度,提高了抵抗角区流动分离的能力。NASA兰利中心低湍流压力风洞(NASA Langley Low-lurbulence Pressure Tun⁃nel,简称LTPT)使用两种方法(吹气和吸气)均实现了展向二维流动的控制[8]。日本国家航空航天试验室(National Aerospace Laboratory in Japan,简称NAL)风洞[12-14]使用边界层抽吸技术实现了模型区自由来流马赫数的均匀性。T.Nishino等[9]使用计算方法研究了在Coanda射流吹气条件下风洞侧壁的干扰效应,研究表明,侧壁对尾缘Coanda射流剖面的影响很小,在流动分离之前,在中间截面周围相当宽的区域内,流动是准二维的。在Coan⁃da射流面与侧壁之间,流动的分离会在壁面卷起两个流向涡,下游这些流向涡的夹带和卷起使得翼型中间截面产生的升力和阻力比二维情况下小。西北工业大学NF-3风洞对侧壁干扰进行了系统性研究,通过吹/吸气方式实现了对侧壁干扰效应的有效控制[15-17]。
考虑到结构强度问题,大厚度翼型[18]在风力机叶片、涡轮叶片、螺旋桨等的应用越来越广泛。可是带尖后缘的大厚度翼型由于转捩提前而导致气动性能表现较差[19],为了提高大厚度翼型的气动特性,减小前缘对转捩的敏感性,人们设计了钝后缘的大厚度翼型[20-22]。大厚度翼型流动分离较早,在风洞试验中,与侧壁边界层之间的干扰更为严重,为了获得可靠的大厚度翼型试验数据,需对其侧壁干扰效应进行控制。
在航空领域,流动控制的方式很多,被动式涡流发生器(Vortex Generator,简称VG)因其结构简单,成本低廉而被广泛应用于边界层发展的控制[23-26]。VG可在主流中引入流向涡,使边界层重新通能并变薄,抵消逆压梯度,最终抑制流动分离。VG的安装位置、高度、展向分布距离均会影响流动控制效果,涡流发生器高度一般与附面层厚度相当或小于附面层厚度。上述研究均使用VG对翼型表面流动或翼型绕流进行控制,而使用VG进行侧壁边界层控制的研究很少,尤其是在大厚度翼型风洞试验方面,就目前掌握的公开资料显示,这种研究尚属首次。
侧壁吹吸气之类的主动控制方式在使侧壁附面层变薄的同时,也减弱了由于模型引起的堵塞效应,但是,需要持续地吸气和合适的吸气量控制。本文采用被动式VG的方法对侧壁干扰进行控制,其对阻塞效应没有影响,可显著减弱或消除侧壁与翼型模型角区的流动分离,考虑到被动式VG的便捷性、实用性和有效性,本文使用的侧壁干扰控制方法是一种成本更低的方法。
本文使用被动式VG对FX77-W-400翼型[19,22]的侧壁干扰效应进行控制,试验雷诺数为Re=3.0×106,提出两种基于VG的侧壁干扰控制构型:侧壁VG和翼面VG,研究VG安装位置对侧壁干扰控制效果和翼型表面压力场细节的影响;并使用POD(Proper Orthogonal Decomposition)技术对不同构型情况下翼型表面压力场结构进行了研究。
1 试验设置
1.1 风洞和模型
试验在西北工业大学NF-3风洞进行。NF-3低速翼型风洞是亚洲最大的低速翼型风洞,翼型试验段长×宽×高为8 m×1.6 m×3 m,为矩形截面,风洞的收缩比为20。该试验段主要性能和流场品质为:最大风速130 m/s,最小稳定风速10 m/s,常 用 风 速60~80 m/s,轴 向 静 压 梯 度0.001 1/m,湍流度0.045%,翼型试验雷诺数可达7.0×106。
FX77-W翼 型 族 是 使 用S.F.Hoerner[21]的 方法设计的一种钝后缘大厚度翼型,本文试验选择FX77-W-400翼型,该翼型最大厚度为40%,最大厚度位置在x/c=40%处,后缘厚度为10.6%,如图1所示。N.Sudani等[5]的研究表明,低马赫数试验情况下,为减小侧壁干扰效应,翼型模型的展弦比至少达到1.5。因此,本文试验模型弦长设计为c=800 mm,展弦比为2.0,同时也保证能够获得足够大的试验雷诺数。
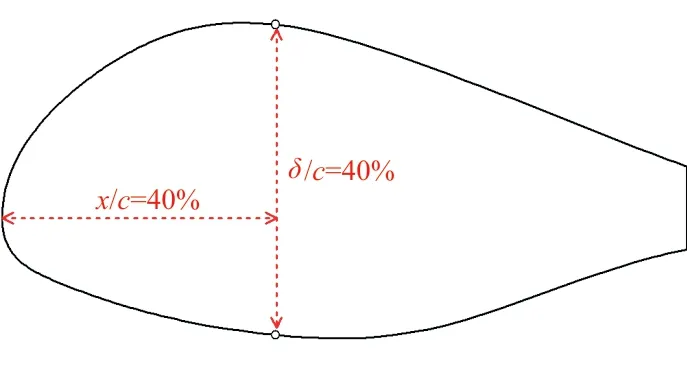
图1 FX77-W-400翼型Fig.1 FX77-W-400 airfoil
取翼型展向50%处作为测压剖面,分布106个测压孔,其中上表面分布50个测压孔,下翼面分布49个测压孔,后缘分布7个测压孔。使用PSI 9816智能压力扫描器对翼型表面压力进行采集,该系统共有736个压力测量通道,采集速度为100 Hz/ch,采集精度为±0.05%。
本文试验不对翼型模型测压截面的附面层进行控制,属于自然转捩。试验雷诺数为Re=3.0×106,迎角变化范围为-2°~20°,Δα=1°。
1.2 涡流发生器
使用被动式VG对风洞侧壁边界层进行控制,并提出两种控制构型:构型Ⅰ(侧壁VG)和构型Ⅱ(翼面VG),其具体形式如表1所示。不使用VG进行控制的称为“Baseline”。

表1 不同构型试验设置Table 1 Experimental setup of different configurations
(1)构型Ⅰ
在风洞侧壁上安装涡流发生器的方式为构型Ⅰ。安装的涡流发生器具体设计参数为:间距D=146 mm,h=30 mm,如图2所示。试验现场安装如图3所示。(2)构型Ⅱ

图2 侧壁VG及其尺寸Fig.2 Sidewall VG and its size

图3 侧壁涡流发生器流动控制试验Fig.3 Flow control experiment of sidewall VG
在翼型上翼面安装涡流发生器的方式为构型Ⅱ。安装的涡流发生器具体设计参数为:间距D=30 mm,h=6 mm,如图4所示。
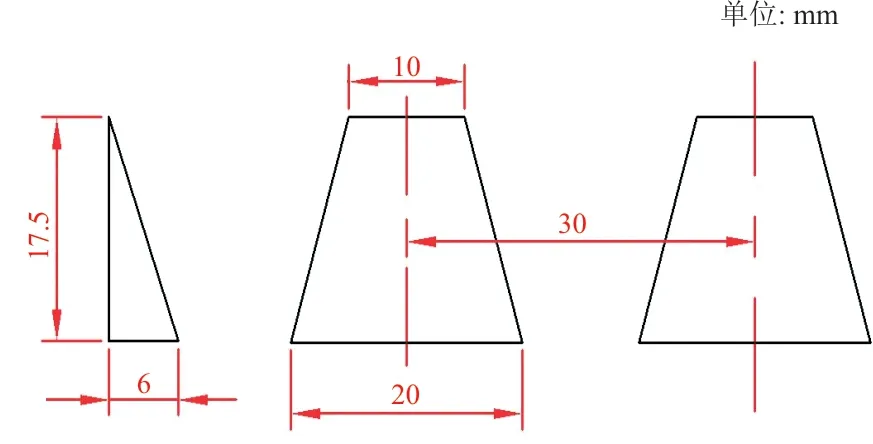
图4 翼面VG及其尺寸Fig.4 Airfoil surface VG and its size
试验目的在于使用VG对侧壁干扰进行控制,关键在于控制侧壁与模型之间的角区流动。因此,涡流发生器安装范围在翼型上表面靠近侧壁区域内,如图5所示。

图5 翼面涡流发生器控制试验Fig.5 Flow control experiment of airfoil surface VG
A.D.Gardner等[10]研究了翼型模型与侧壁之间的缝隙对角区流动的影响,研究表明,这种缝隙对翼型模型端部近壁面三维流动拓扑结构有着显著影响,无缝隙时侧壁干扰则最小。为了减小侧壁干扰效应,本文选择无缝隙模型安装方式(如图5所示)。
2 试验结果及数据分析
2.1 无控制情况
本文就基准翼型试验结果与文献[19,22]数据进行对比,如图6所示,红色圆圈为斯图加特大学(Stuttgart University)使用风洞侧壁边界层吹除装置控制侧壁边界层情况下的翼型升力系数结果[22];红色虚线为F.Grasso[22]使用RFOIL代码进行数值计算的结果;蓝色方框为T.Winnemöller等[19]使用T.Pulliam和J.Steger发展的ARC2D代码[27]进行全湍流条件的计算结果;黑色实线为本文试验结果(未进行侧壁干扰控制)。斯图加特大学、F.Grasso和本文结果的雷诺数均是Re=3.0×106,而T.Winnemöller等 的 计 算 雷 诺 数 是Re=1.0×106。
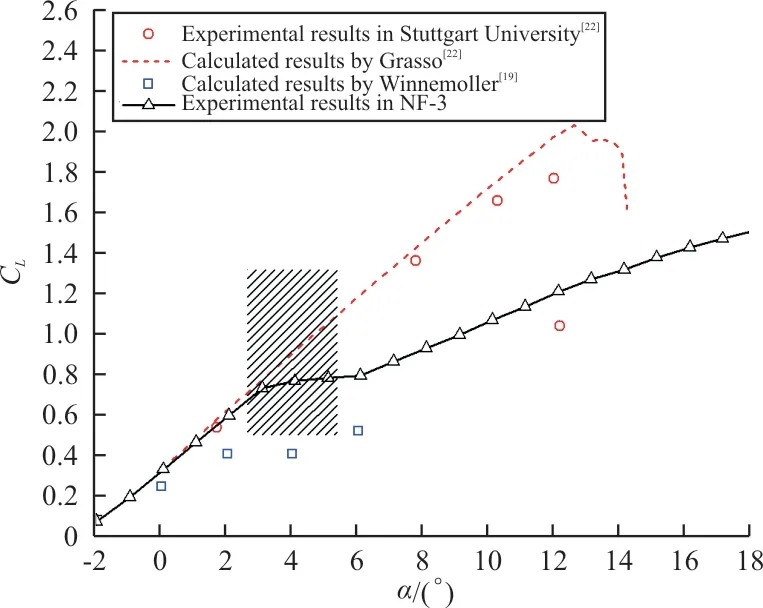
图6 本文试验结果与文献结果对比Fig.6 Comparison between experimental results in this article and results in other literatures
从图6可以看出:小迎角范围内(α≤3°),本文试验结果(没有进行过侧壁干扰控制)与斯图加特大学和F.Grasso(进行过侧壁边界层控制)的结果一致;而在α>3°范围内,本文试验结果表明,翼型提前失速,其气动特性开始与斯图加特大学和F.Grasso的结果有显著不同。比较本文试验与斯图加特大学的试验条件与结果,认为这种差距是由侧壁干扰引起的。对比T.Winnemöller等的计算结果,在大范围的迎角范围内,与本文试验、斯图加特大学试验和F.Grasso的计算结果均有显著差异,这种差异应该是雷诺数不同和全湍流计算条件引起的。
对于基准翼型(无控制情况),在α为-2°~3°之间是明显的线性区(如图6所示),流动呈现附着流状态。在α为3°~6°范围内(图6中的阴影部分),升力系数没有显著提高,力矩系数增加,而阻力系数没有显著增大,如图7所示,因此这个阶段的气动性能应该不是流动分离导致的,因为如果流动发生分离,阻力会显著增加,这在压力分布上也可以看出,如图8所示。
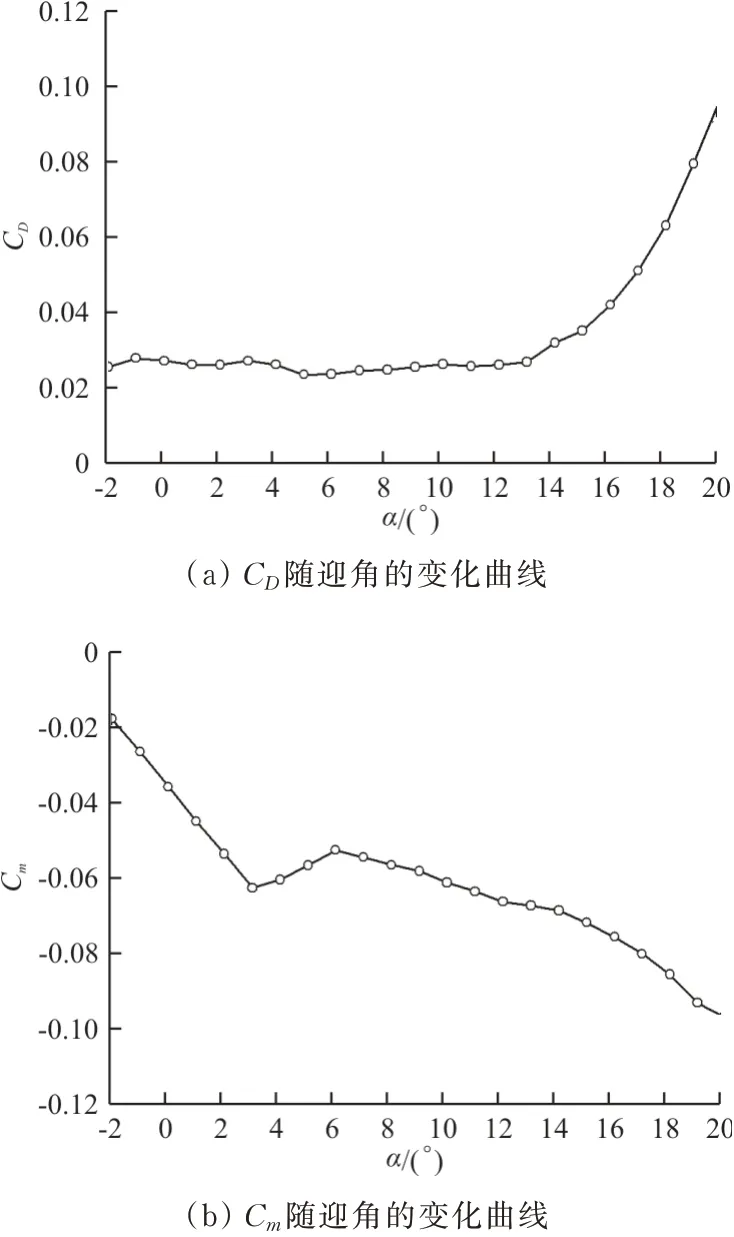
图7 基准翼型的阻力系数和力矩系数Fig.7 Drag and moment coefficients of reference airfoil
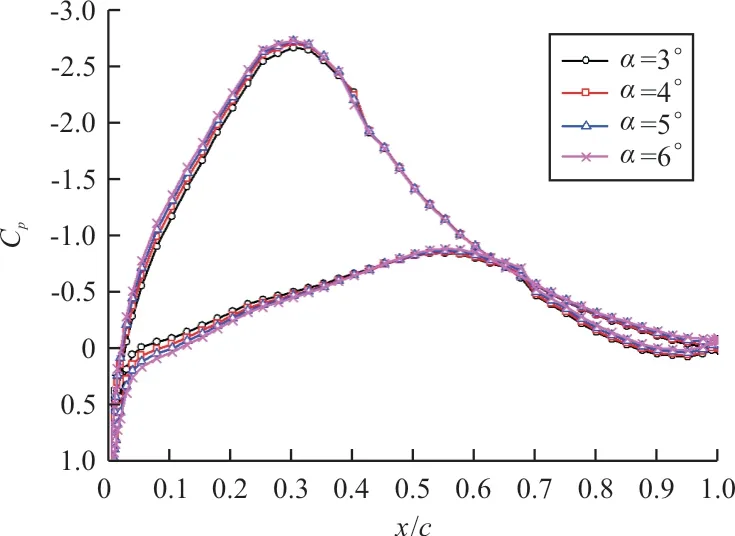
图8 典型迎角处的压力系数分布Fig.8 Cp distribution at typical AOAs
在这个阶段,上翼面维持附着流形态,没有呈现流动分离导致的压力平台特征,只不过压力系数分布基本一致,仅在顺压梯度区有轻微变化,导致该阶段升力系数没有显著增加,力矩系数变大。可见,该阶段这种失速的特征并不是由流动分离引起的,而是翼型吸力面吸力不够导致的,导致吸力不够的原因为角区流动[4-8]的出现。角区流动沿横向的发展使得翼型不再维持二维流动,翼型升力线斜率开始明显减小。而角区流动发生的原因在于风洞侧壁的影响,因此需要对侧壁干扰进行控制。
2.2 侧壁VG控制
本节使用构型Ⅰ对风洞侧壁干扰进行控制,研究VG安装位置对控制效果的影响。
不同安装位置情况下的翼型气动特性如图9所示。

图9 侧壁VG对翼型气动特性的影响Fig.9 Effect of sidewall VG on aerodynamic characteristics of airfoil
从图9可以看出:
(1)对比基准翼型,侧壁VG安装在翼型前缘(x/c=0%)时,改变了翼型在小迎角范围内的升力线斜率和力矩系数形态,使α为0°~3°的升力线斜率减小,说明在该阶段横流就已经产生。在大迎角情况下,VG安装在x/c=0%也没有起到显著的控制作用。另外,对阻力系数几乎没有影响。可见,相较于基准翼型,该位置的侧壁VG控制形式产生了负作用:小迎角情况下使横流提前发生,大迎角情况下几乎没有影响。
(2)侧壁VG安装在翼型最大厚度位置(x/c=40%)时,相较于基准翼型,延迟了升力系数和力矩系数的失速,由αstall=3°延迟到了αstall=7°。在α>7°时,升力线斜率开始明显减小。注意到这个过程中,阻力系数并没有显著增大,说明这种失速也是由横流引起的。可见,侧壁VG安装在翼型最大厚度位置起到了显著的侧壁干扰控制效果,使失速延迟了Δα=4°。
基准翼型及经侧壁VG控制后的试验结果与参考文献的结果对比如图10所示,可以看出:本文使用被动式VG对侧壁干扰进行控制的效果尽管没有斯图加特大学应用边界层吹吸的结果那么理想,但仍能够获得△α=4°的失速延迟,考虑到本文使用的是一种极为简便的被动式控制方法,可以认为这种控制方式还是极有潜力的。
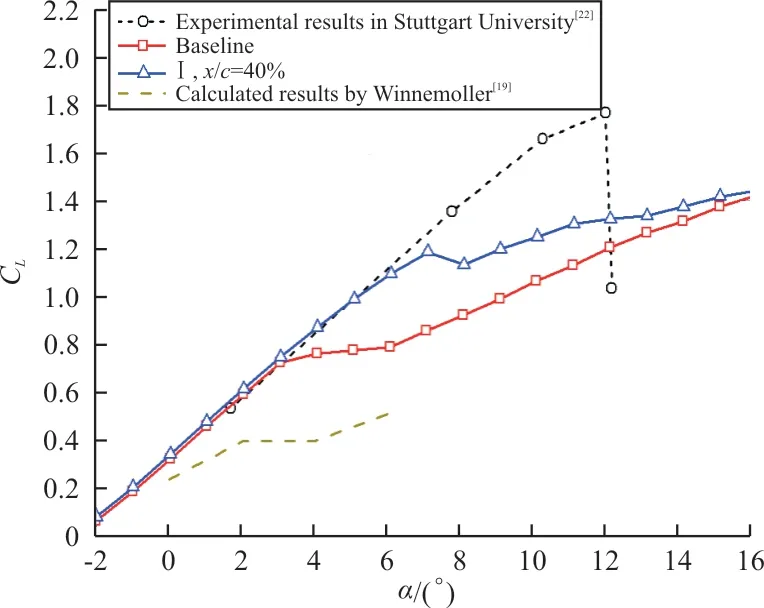
图10 本文与文献结果对比Fig.10 Comparison of results in this article and other literatures
除整体气动特性外,侧壁VG对转捩位置、吸力峰位置和吸力峰值等气动特征也会产生影响。使用逆压梯度区逆压梯度突然增大[28-31]的位置作为转捩位置,如图11所示。

图11 转捩位置判断Fig.11 Judgment of transition position
侧壁VG不同安装位置情况下翼型上表面压力场如图12所示,蓝色散点是转捩位置,红色散点是吸力峰位置。可以看出:侧壁VG没有影响全迎角范围内翼型上表面的压力形态,但对具体的流动细节有影响;另外,侧壁VG安装在x/c=40%情况下,小迎角范围(α为0°~5°)内吸力峰值的梯度更大。

图12 侧壁VG对吸力面压力场的影响Fig.12 Effect of sidewall VG on pressure field of suction surface
不同侧壁VG安装位置对流动特征的影响如图13所示,其中(a)是转捩位置,(b)是吸力峰位置,(c)是吸力峰值。侧壁VG安装在x/c=0%时对转捩位置没有影响(图10),因此没有在图13中表现。从图13(a)可以看出:VG安装在翼型最大厚度位置(x/c=40%)使得α=5°时的转捩位置提前;从图13(b)可以看出:两种安装位置VG均会影响大迎角情况下吸力峰位置,使吸力峰位置前移,且安装在最大厚度位置处,吸力峰位置最早发生前移的迎角最小,为α=9°,相较于基准翼型,提前了Δα=2°(基准翼型为α=11°);从图13(c)可以看出:吸力峰值与升力系数变化趋势一致,侧壁VG安装在最大厚度位置(x/c=40%)时,吸力峰值在α为-2°~7°范围内均保持线性增长。
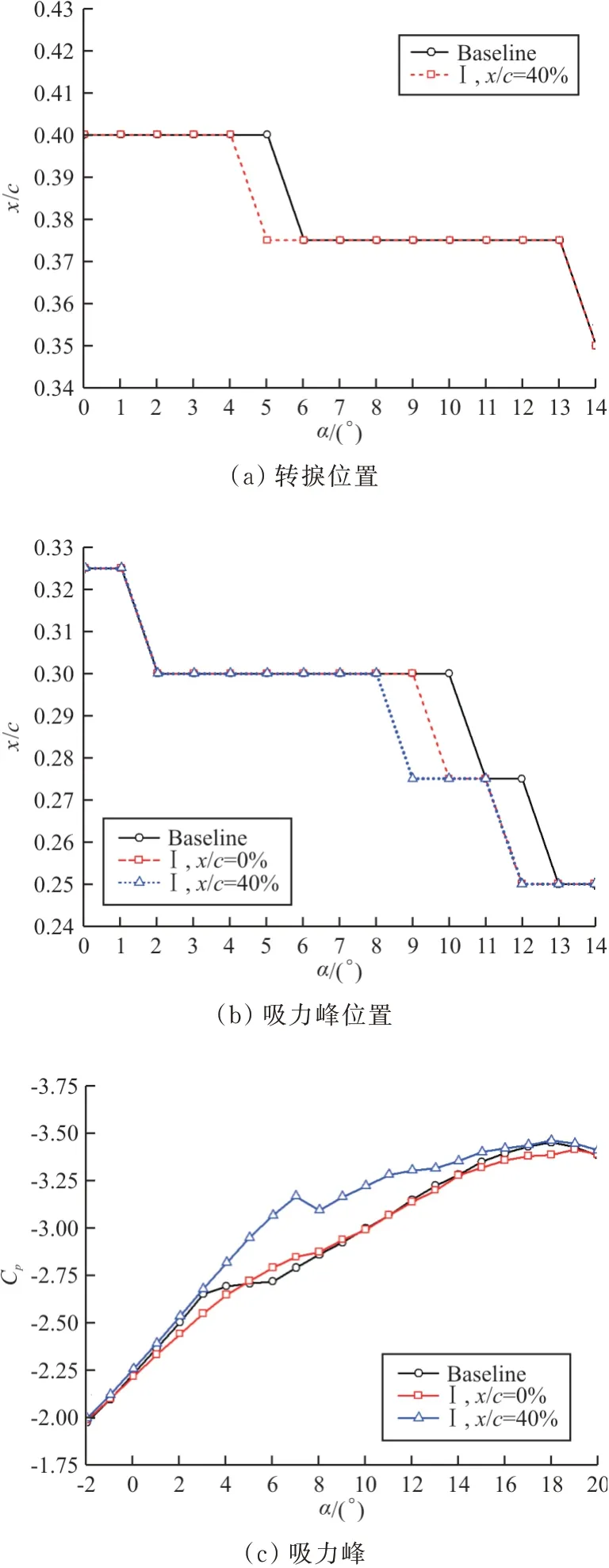
图13 侧壁VG对流动特征的影响Fig.13 Effect of sidewall VG on flow characteristics
典型迎角情况下的压力系数分布如图14所示。本文使用的FX77翼型为大厚度(40%)翼型,较大的前缘半径使翼型维持层流的能力增强;且最大厚度位置靠后(x/c=40%),使顺压梯度范围增大。从图14可以看出:侧壁VG不影响翼型表面的压力形态,只是对压力系数的具体数值产生影响,尤其是安装在最大厚度位置时;对于基准翼型,由于横流的影响(侧壁干扰),小迎角范围内(α为3°~6°)上表面吸力峰值较小,导致失速;使用侧壁VG(安装在x/c=40%)进行控制后,翼型上表面吸力峰明显增大,失速延迟Δα=4°,展现出理想的侧壁干扰控制效果。
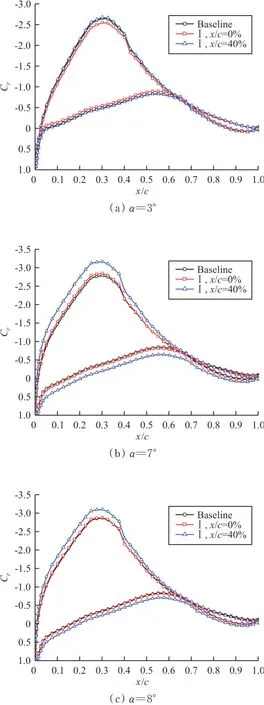

图14 侧壁VG对典型迎角下翼型压力系数分布的影响Fig.14 Effect of sidewall VG on Cp distributions at typical AoAs
2.3 翼面VG控制
在翼型上表面安装VG时,仅在角区附近安装翼面VG安装位置对翼型气动性能的影响如图15所示。
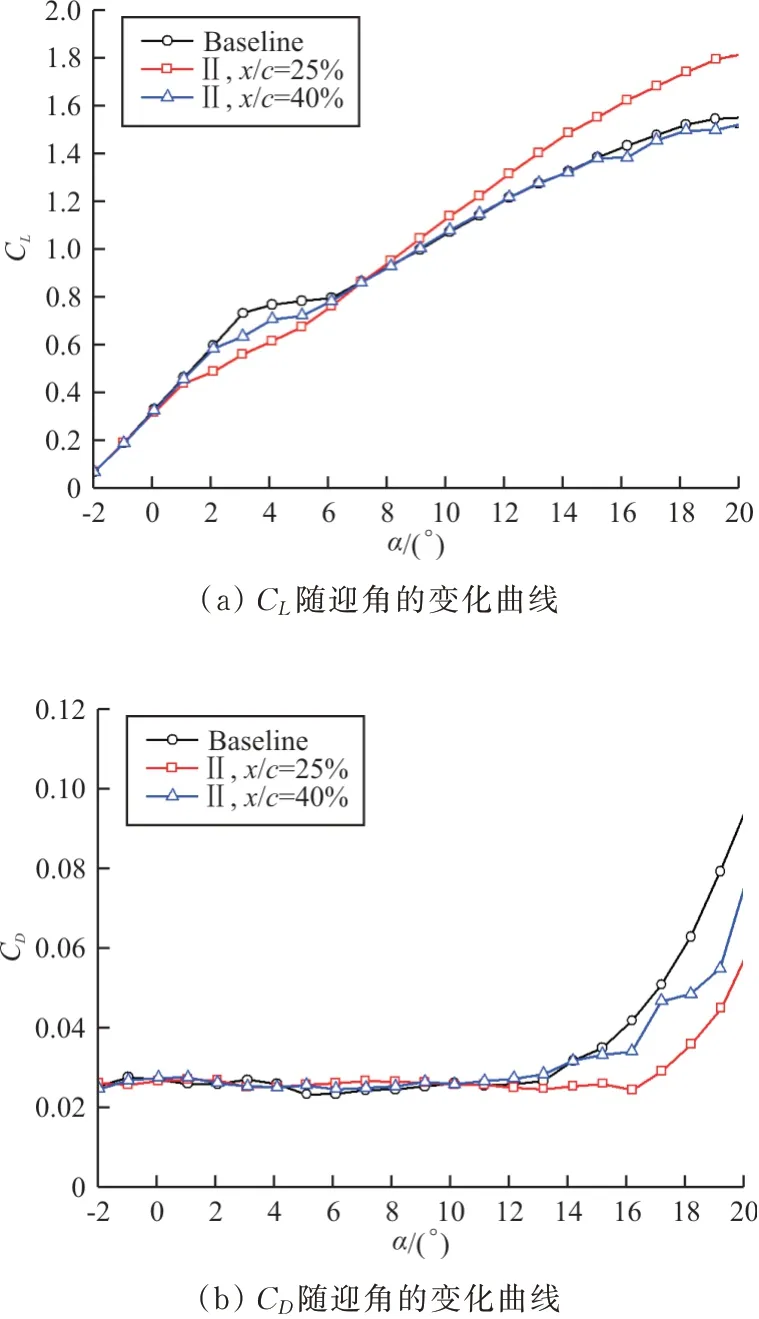
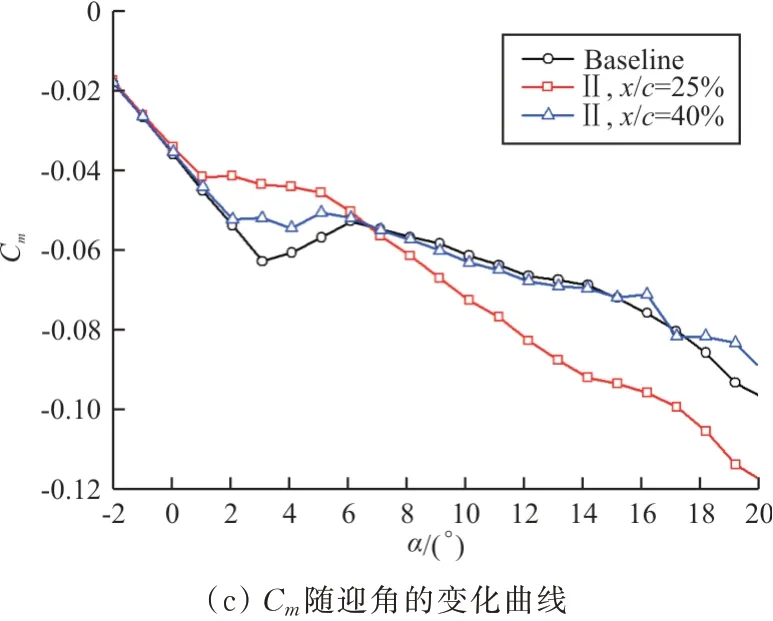
图15 翼面VG对翼型气动特性的影响Fig.15 Effect of airfoil surface VG on aerodynamic characteristics of airfoil
从图15可以看出:
(1)对比基准翼型,翼面VG安装在x/c=25%时,改变了翼型在全迎角范围(α为1°~20°)内的升力线斜率和力矩系数形态,使α为0°~3°的升力线斜率减小,说明在该阶段,横流就已经产生。在α>3°时,翼面VG使得升力线斜率较基准翼型显著提高,说明在上述迎角范围内,经VG控制后的横流要明显弱于基准翼型(未经控制),这也使得在大迎角情况下(α>8°),翼型升力系数较基准翼型显著提高。并且,该位置(x/c=25%)下的翼面VG对α为-2°~12°范围内阻力系数几乎没有影响,且显著延迟了阻力发散。可见,相较于基准翼型,该位置的翼面控制形式对小迎角的侧壁干扰起负作用,而对大迎角范围起到了显著的控制作用。
(2)翼面VG安装在翼型最大厚度位置(x/c=40%)时,相较于基准翼型,升力线斜率提前减小,力矩系数形态提前变化,且对大迎角下的翼型气动性能几乎没有影响。可见,该位置的翼面VG对侧壁干扰控制起到了负作用。
翼面VG不同安装位置情况下的翼型上表面压力场如图16所示,蓝色散点是转捩位置,红色散点是吸力峰位置。可以看出:与侧壁VG一样,翼面VG没有影响全迎角范围内翼型上表面的压力形态;翼面VG安装在x/c=25%时,大迎角下的吸力峰值更大,这也使得大迎角情况下翼型升力系数较基准翼型大。
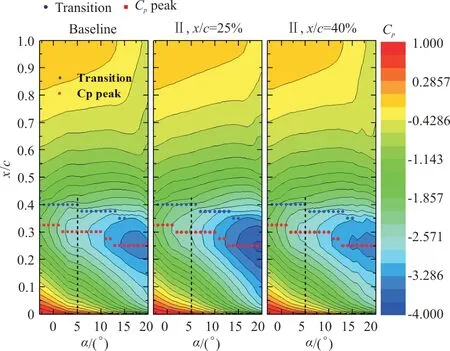
图16 翼面VG对翼型吸力面压力场的影响Fig.16 Effect of airfoil surface VG on pressure field of suction surface
不同翼面VG安装位置对流动特征的影响如图17所示,其中(a)是转捩位置,(b)是吸力峰值。本文使用的翼面VG对吸力峰位置没有影响(图16),因此没有在图17中表现。从图17(a)可以看出:x/c=25%位置的翼面VG使得α=6°时的转捩位置较基准翼型靠后,即延迟了x/c=0.375位置处的转捩。从图17(b)可以看出:吸力峰值与升力系数变化趋势一致,翼面VG安装在x/c=25%时,减小了小迎角范围内的吸力峰值,提高了大迎角情况下的吸力峰值。

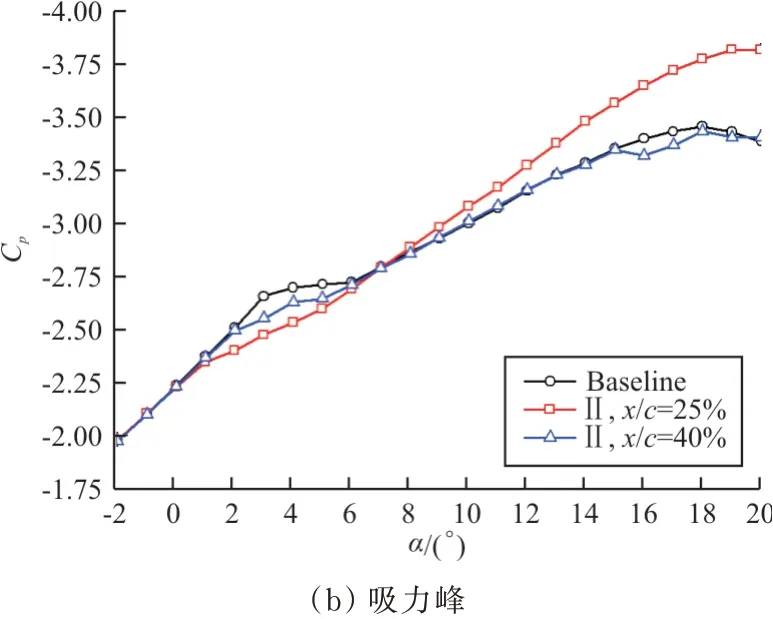
图17 翼面VG对流动特征的影响Fig.17 Effect of airfoil surface VG on flow characteristics
典型迎角情况下的压力系数分布如图18所示,可以看出:与侧壁VG的影响相同,翼面VG也不影响翼型表面的压力形态,只是对压力系数的具体数值产生影响,尤其是翼面VG安装在x/c=25%时;使用翼面VG(安装在x/c=25%)进行控制后,小迎角情况下翼型上表面吸力峰减小,表明横流提前发生;而在大迎角情况下,吸力峰值较基准翼型显著提高,说明经该位置(x/c=25%)的翼面VG控制后,横流明显减弱,体现了较好的控制效果。
由前文的压力系数分布曲线可知,该翼型上表面顺压梯度范围较长,本文将翼面VG安装在x/c=25%,位于顺压梯度区,该范围内,VG能够更好地对侧壁产生的干扰(横流)进行控制。


图18 翼面VG对典型迎角下翼型压力系数分布的影响Fig.18 Effect of airfoil surface VG on Cp distributions at typical AOAs
综上所述,在本文试验范围内,安装在x/c=40%位置的侧壁VG可有效改善小迎角范围内的侧壁干扰情况,使失速推迟Δα=4°;安装在x/c=25%位置的翼面VG可有效改善大迎角情况下的侧壁干扰情况,显著提高大迎角情况下的CL,并推迟了阻力发散。
2.4 压力形态分析
构型Ⅰ和构型Ⅱ不影响翼型表面的压力形态(如图14和图18所示),但是会对吸力峰值的发展形态产生影响(如图13(c)和图17(b)所示)。对比图9(a)和图13(c),以及图15(a)和图17(b),发现升力系数和吸力峰值的变化趋势一致,因此对其进行相关性分析,如图19所示。
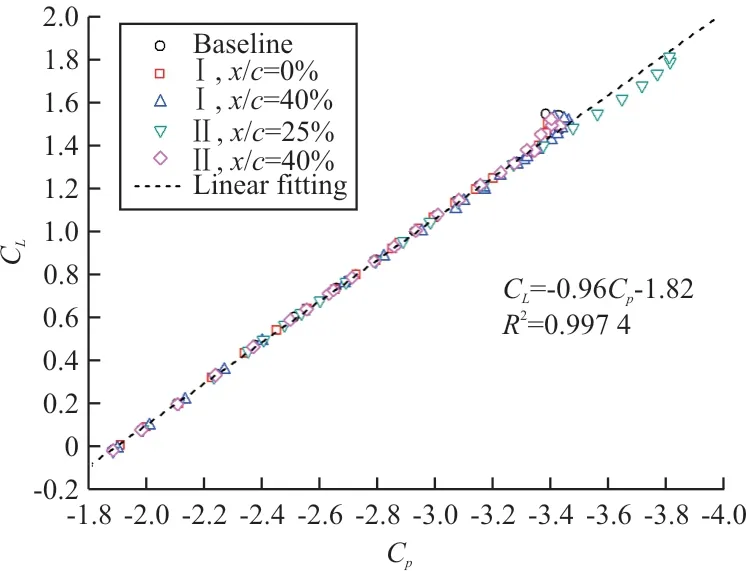
图19 吸力峰值与CL之间的相关性Fig.19 Correlation of suction peak and CL
从图19可以看出:各种构型下的升力系数和吸力峰值存在一致的线性相关性,决定系数可达R2=0.997 4。对于本文的试验情况,翼型典型的气动特性与吸力峰值直接相关,侧壁干扰引起的横流导致基准翼型(未控制)吸力峰值不够,在迎角较小(α=3°)时就发生失速。而安装在x/c=40%的侧壁VG和安装在x/c=25%的翼面VG可分别改善小迎角和大迎角情况下横流情况,使得吸力峰值提高,进而提高了升力系数。
构型Ⅰ和构型Ⅱ不仅对吸力峰值的发展形态有影响,还对后缘点压力的发展有影响。本文试验模型是钝后缘,在试验模型后缘分布7个测压孔,考察这7个测点压力的发展形态,发现其影响规律一致,因此取上表面后缘和下表面后缘两个测点进行说明,如图20所示,可以看出:在α为2°~12°范围内,上下壁面后缘点压力发展形态有显著差异,安装在x/c=40%位置的侧壁VG构型(构型Ⅰ,图中蓝色线)使后缘点压力在较大迎角范围内维持在Cp=0左右;而安装在x/c=25%位置的壁面VG构型则使这个迎角范围变小;在α>12°范围内,安装在x/c=25%位置的壁面VG构型的后缘压力与其他四种情形显著不同,其压力值较其他情况显著增大。
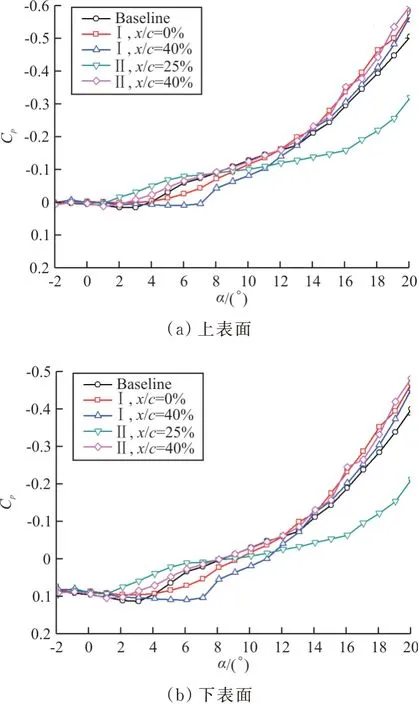
图20 不同构型情况下后缘压力形态演化Fig.20 Evolution of trailing edge pressure of different configurations
2.5 POD分析
为了更好地观察翼型表面的压力结构,本文使用POD[32-33]技术对表面压力场进行分析。
设翼型表面压力场为
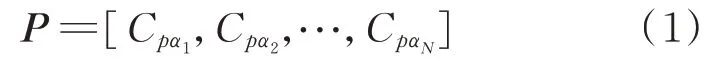
式中:N为迎角数量,也是POD分析的数据维数,本文试验中,迎角范围为-2°~20°,间隔Δα=1°,因此,N=23;Cpαi为第i个迎角下的翼型压力系数,本文试验共有106个测压点,因此Cpαi是一个包含106个压力系数信息的列向量。因此,本文进行POD分析的样本大小为106×23。
对于式(1)中的压力场P,其中某一维数据可表示为
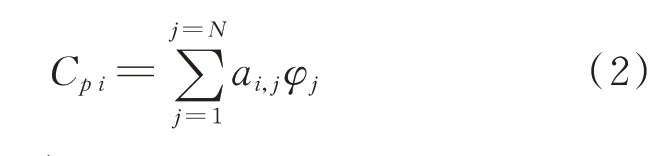
式中:φ为一组正交基。
本 文 使 用L.Sirovich[34]提 出 的snapshots方 法对上述问题进行求解。
安装在x/c=40%的侧壁VG(构型Ⅰ)和安装在x/c=25%的翼面VG(构型Ⅱ)对侧壁干扰有不同程度的控制效果,因此对这两种构型和基准翼型的表面压力系数分布进行POD分析。
不同构型的POD能谱如图21所示,可以看出:不管是哪种构型,第一模态(主模态)均能占据85%以上的能量,而前三阶模态可达99.96%以上的能量,因此,取前三阶POD模态进行分析。

图21 不同构型情况下的POD能谱Fig.21 POD energy spectrum of different configurations
前三阶POD模态及系数如图22所示,(a)和(b)分别为第一模态和第一模态系数,(c)和(d)分别为第二模态和第二模态系数,(e)和(f)分别为第三模态和第三模态系数。
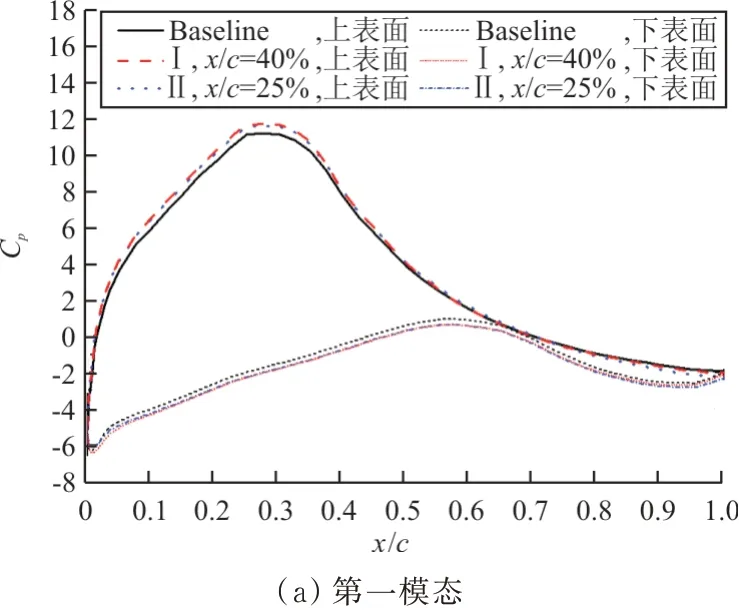

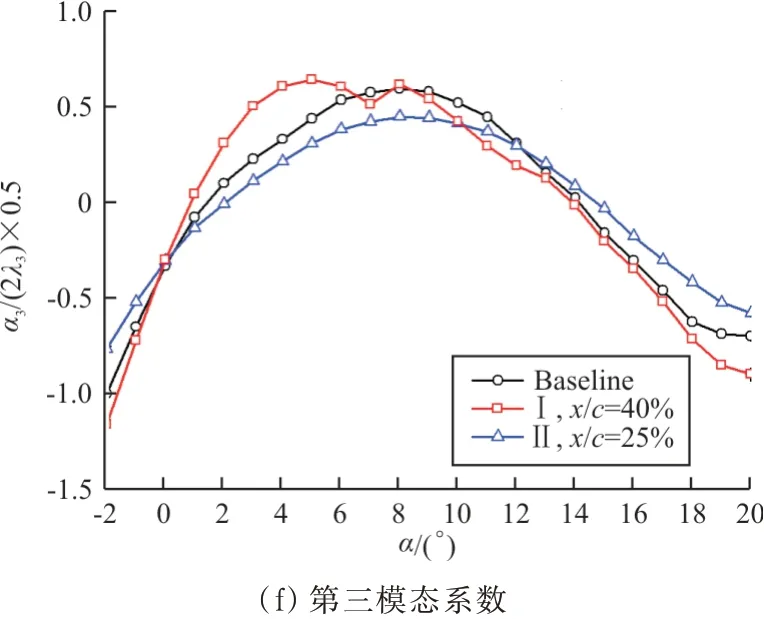
图22 POD模态与对应的模态系数Fig.22 POD modes and their corresponding modal coefficients
从图22可以看出:
三种构型的第一模态基本一致,由压力系数形态看,该模态属于附着流模态。基准翼型的第一模态系数绝对值随迎角增大而逐渐增大,在α=3°时,基本不变,对比翼型升力系数,该位置升力系数基本不变。安装在x/c=40%的构型Ⅰ在α=7°时绝对值明显减小,该构型升力系数在α=7°也明显减小;安装在x/c=25%的构型Ⅱ在较大范围迎角内表现出连续单调变化的形态。第一模态系数同样表明,该模态是附着流模态。
对于第二模态,基准翼型与安装在x/c=40%的构型Ⅰ的形态基本一致,安装在x/c=25%的构型Ⅱ的下表面压力系数表现出不同的形态。基准翼型与安装在x/c=25%的构型Ⅱ在大迎角范围内的气动性能显著不同(见图15),因此,该模态是大迎角情况下的流动模态。在x/c为0.10~0.65范围内,第二模态上表面呈现出明显的压力平台特征,说明该模态是分离流模态,该模态主导大迎角情况下的流动。另外,三种构型的第二模态系数变化趋势基本一致,均在α=10°附近变号,系数由负变正的这种变化使得第二模态上表面大范围内的压力系数由逆压梯度变为顺压梯度,同样表明该模态是分离流模态。
对于第三模态,其形态较为复杂,最为显著的特征表现在上表面x/c为0.35~0.40范围和下表面x/c为0.65~0.70范围内,该范围内压力梯度明显变化,对比图9可知,上表面x/c为0.35~0.40范围和下表面x/c为0.65~0.70范围分别属于上表面和下表面的转捩位置,可见,该模态是流动转捩模态。另外,第三模态系数在小迎角范围(α为4°~6°)内表现出明显不同,该阶段三种构型的转捩位置也有所不同,因此该模态是转捩模态。
以基准翼型(未控制)为例,使用前三阶模态对试验结果进行重构,如图23所示,可以看出:小迎角情况(α=0°)下,使用前三阶模态的重构结果可以捕捉到上下翼面的转捩特征;在α=5°和α=12°时,重构结果可以准确描述上下翼面的附着流动;α=20°时,重构结果对上下翼面的分离流形态也能够准确描述。可见,在全迎角范围内,使用前三阶模态(附着流模态、分离流模态和转捩模态)的重构结果能够表征试验结果的主要特征。
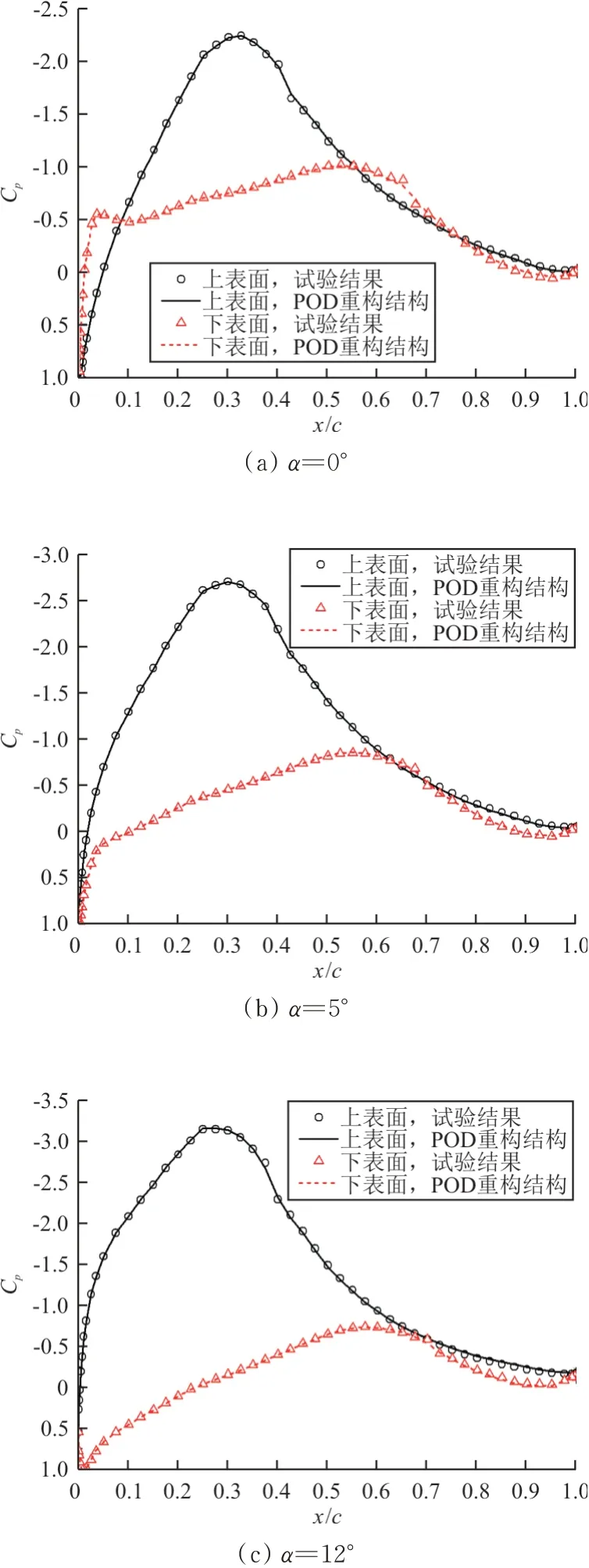
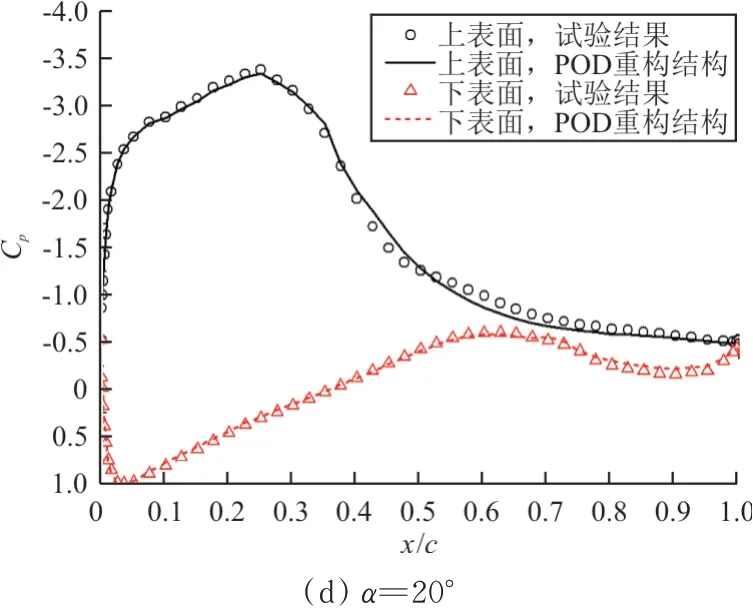
图23 基准翼型前三阶模态重构结果与试验结果对比Fig.23 Comparison of reconstruction results using first three modes and experimental results of reference airfoil
综上所述,使用构型Ⅰ和构型Ⅱ可以对侧壁干扰(横流)进行有效控制;POD分析表明,这种侧壁干扰控制形式保持了基准翼型表面流动的主要结构,三种构型情况下(基准翼型、构型Ⅰ和构型Ⅱ),第一模态(主模态)为附着流模态,第二模态为分离流模态,第三模态为转捩模态。
3 结论
(1)首次使用被动式VG对侧壁干扰进行有效控制。安装在x/c=40%位置的构型Ⅰ可有效改善小迎角范围内的侧壁干扰情况,使翼型上表面吸力峰明显增大,失速推迟Δα=4°。
(2)构型Ⅰ和构型Ⅱ对翼型表面的吸力峰值有影响。在本文研究范围内,升力系数和吸力峰值之间存在显著的线性相关性。
(3)POD分析表明,本文使用的侧壁干扰控制形式保持了基准翼型表面流动的主要结构,三种构型情况下(基准翼型、构型Ⅰ和构型Ⅱ),第一模态(主模态)为附着流模态,第二模态为分离流模态,第三模态为转捩模态。
